铁道货车非线性稳定性

王勇; 曾京; 张卫华

铁道货车非线性稳定性

西南交通大学牵引动力国家重点实验室, 四川成都 610031

基金项目:

教育部跨世纪优秀人才培养基金资助项目教技函[2000]1号

详细信息

作者简介:
王勇(1972-), 男, 辽宁丹东人, 西南交通大学博士生, 从事机车车辆动态模拟、计算机控制和仿真研究

中图分类号: U270.11
计量
- 文章访问数: 266
- HTML全文浏览量: 84
- PDF下载量: 522
- 被引次数: 0
出版历程
- 收稿日期: 2001-12-05
- 刊出日期: 2002-06-25

Nonlinear stability of railway freight cars

National Traction Power Laboratory, Southwest Jiaotong University, Chengdu 610031, China

More Information

Author Bio:
WANG Yong(1972-), male, a doctoral student of Southwest Jiaotong University, engaged in research of railway vehicle dynamics

摘要

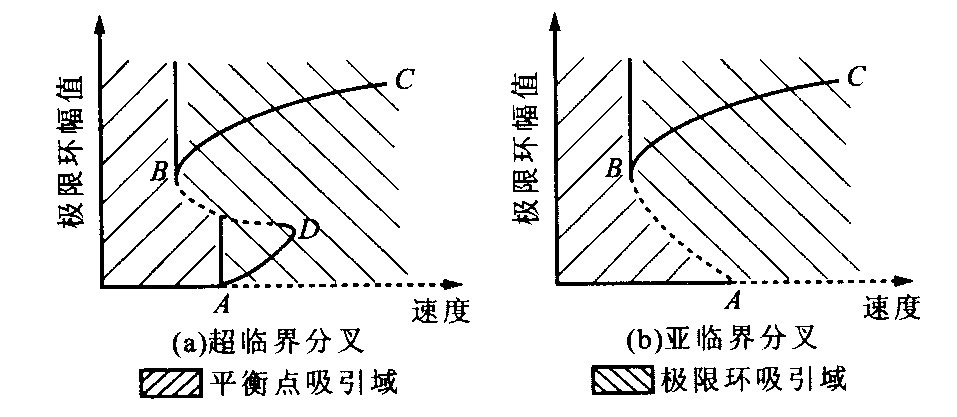
摘要: 建立了具有35个自由度的三大件转向架货车系统通用非线性数学模型, 可用于分析普通三大件转向架、侧架交叉支撑转向架、自导向和迫导向径向转向架货车的非线性动力学特性。模型充分考虑了轮轨相互作用关系及悬挂系统的非线性因素, 运用数值分叉理论分析车辆系统的非线性运动稳定性, 对各导向机构和交叉支撑机构对三大件转向架货车运动稳定性的影响分别进行了研究, 同时对货车系统有可能出现的准周期解及混沌运动也进行了探讨
- 货车通用计算模型 /
- 稳定性 /
- 分叉 /
- 混沌
Abstract: A nonlinear genetic mathematical model for three piece bogie freight car with 35 degrees of freedom is set up, which can be utilized to analyze the nonlinear dynamic behavior of conventional, cross bracing, self steering and forced steering bogies respectively.The nonlinearities arising due to the wheel/rail interactions and suspension parameters of vehicle system are considered.Numerical bifurcation theory is used for analyzing the nonlinear stability behavior of the freight car.Then the influences of steering and cross bracing mechanisms on the stability of the three piece bogie freight car are studied, and the quasi periodic solutions, chaos in the system are discussed as well.
- generic model of freight cars /
- stability /
- bifurcation /
- chaos

HTML全文

图 1 车辆系统典型分叉情况

Figure 1. Typical bifurcation diagrams for railway vehicle system

下载: 全尺寸图片幻灯片

图 2 迫导向机构计算模型

Figure 2. Forced-steering mechanism model

下载: 全尺寸图片幻灯片

图 3 货车通用计算模型

Figure 3. Generic mathematical model for freight cars

下载: 全尺寸图片幻灯片

图 4 四种转向架临界速度比较

Figure 4. Comparison of critical speeds

下载: 全尺寸图片幻灯片

图 5 导向刚度的影响

Figure 5. Influence of stiffness of forced-steering mechanism

下载: 全尺寸图片幻灯片

图 6 导向增益的影响

Figure 6. Influence of gain of forced-steering mechanism

下载: 全尺寸图片幻灯片

图 7 自导向交叉杆刚度的影响

Figure 7. Influence of stiffness of self-steering mechanism

下载: 全尺寸图片幻灯片

图 8 侧架交叉支撑刚度的影响

Figure 8. Influence of crossbracing stiffness

下载: 全尺寸图片幻灯片

图 9 常规三大件转向架货车分叉图

Figure 9. Bifurcation diagram of conventional three-piece bogie freight car

下载: 全尺寸图片幻灯片

图 10 轮对横移时间历程图

Figure 10. Time histories of lateral displacement of wheelset

下载: 全尺寸图片幻灯片

图 11 轮对横移相平面图

Figure 11. Phase plane projections of wheelset lateral motion

下载: 全尺寸图片幻灯片

参考文献(9)

[1]	ZENG Jing, WANG Yong. Nonlinear dynamic analysis for railway freight cars[J]. Journal of Southwest Jiaotong University, 2000, 35(4): 399-403.
[2]	ZENG Jing. Numerical computations of the hunting bifurcation and limit cycles for railway vehicle system[J]. Journal of The China Railway Society, 1996, 18 (3): 13-19.
[3]	HUANG Cheng-rong, ZHAN Fei-sheng. The numerical bifurcation method of nonlinear lateral stability of a locomotive[J]. Journal of The China Railway Society, 1994, 16(2): 1-5.
[4]	ZHANG Wei-hua, SHEN Zhi-yun. Nonlinear stability analysis of railway vehicle system[J]. Journal of the China Railway Society, 1996, 18(1);29-34.
[5]	Huns True. Chaotic motion of railway vehicles[A]. Proc. of 11th IAVSD Symposium[C]. Canada, 1989: 578-587.
[6]	Carsten Nordstrom Jensen, Hans True. On a new route to chaos in railway dynamics[J]. Nonlinear Dynamics, 1997, 13(2): 117-129. doi: 10.1023/A:1008224625406
[7]	陆启韶. 常微分方程的定性方法和分叉[M]. 北京: 航空航天大学出版社, 1989.273-277.
[8]	陈式刚. 映象与混沌[M]. 北京: 国防工业出版社, 1992.1-12.
[9]	WANG Yong. Nonlinear stability study of three-piece bogie freight cars[D]. Chengdu: Southwest Jiaotong University, 1998.