车轮型面动态高速曲线通过性比较

张剑; 孙丽萍

车轮型面动态高速曲线通过性比较

张剑^{1, 2,},
孙丽萍²

1.
西南交通大学牵引动力国家重点实验室, 四川成都 610031
2.
大连交通大学交通运输工程学院, 辽宁大连 116028

基金项目:

铁道部科技研究开发计划项目 Z2006-049

牵引动力国家重点实验室开放基金项目 TPL0503

详细信息

作者简介:
张剑(1968-), 男, 甘肃宁县人, 大连交通大学副教授, 工学博士研究生, 从事车辆动力学研究

中图分类号: U211.5
计量
- 文章访问数: 350
- HTML全文浏览量: 115
- PDF下载量: 240
- 被引次数: 0
出版历程
- 收稿日期: 2007-06-02
- 刊出日期: 2007-12-25

Comparison of dynamic high-speed curving properties for wheel profiles

ZHANG Jian^{1, 2
,},
SUN Li-ping²

1.
Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, Sichuan, China
2.
School of Traffic and Transportation, Dalian Jiaotong University, Dalian 116028, Liaoning, China

More Information

Author Bio:
Zhang Jian(1968-), male, associate professor, doctoral student of engineering, + 86-411-84106938, zhangjian@djtu.edu.cn

摘要

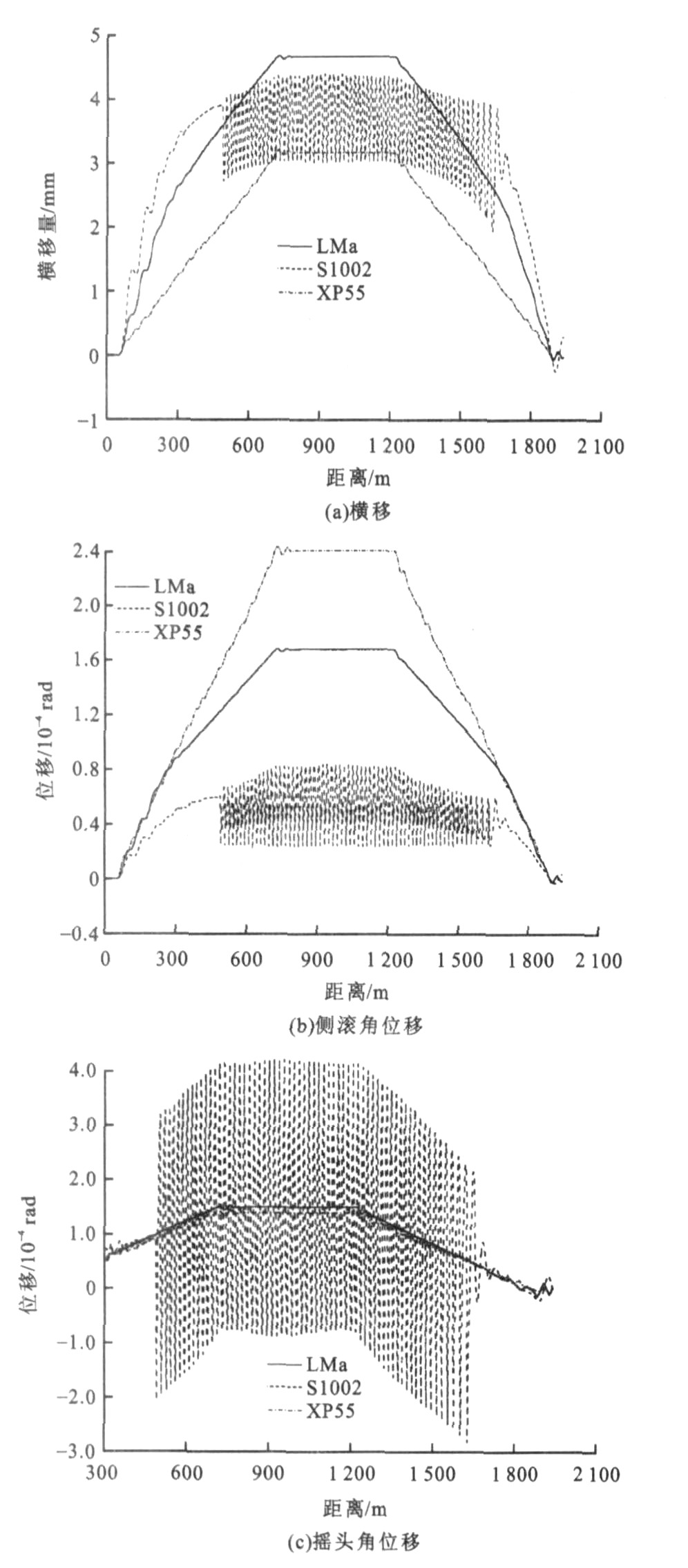
摘要: 为了有效选择高速车轮型面, 通过车辆轨道系统动力学仿真得到轮对高速通过曲线的运动状态, 利用运动状态参量进行三维轮轨接触几何特性与蠕滑率计算, 用Contact程序进行轮轨非赫兹滚动接触计算, 分析了LMa、S1002和XP55车轮型面高速曲线通过匹配特点。分析结果表明: LMa和XP55型面轮对运动参数曲线平滑, S1002型面出现大幅度波动, 并产生蛇行运动; 当轮对横移量为3. 0~3. 5 mm时, S1002型面轮轨接触点对产生约11 mm跳跃, 正好处于钢轨型面R300、R80 mm圆弧过渡区; S1002型面接触斑基本处于滑动状态, LMa型面接触应力最小, XP55型面接触应力最大。可见S1002型面与中国60 kg·m^-1钢轨不匹配, LMa型面匹配效果最理想, XP55型面匹配相对较好。
- 车辆工程 /
- 轮轨型面 /
- 滚动接触 /
- 轮轨关系 /
- 车辆轨道动力学
Abstract: In order to effectively choose wheel profiles, the high-speed curving characteristics of wheelset were obtained by vehicle-track coupling dynamics simulation, wheel/rail contact geometry property and creeping ratio were calculated with wheelset curving dynamic parameters, wheel/rail non-Hertzian rolling contact was analyzed by using Contact program, and the high-speed curving matching characteristics of LMa, S1002 and XP55 wheel profiles were studied.Analysis result shows that the curves of wheelset dynamic parameters for LMa and XP55 profiles are smooth, S1002 profile exhibits large amplitude oscillation, and hunting occurs; wheel/rail contact point of S1002 profile jumps 11 mm while wheelset laterally displaces from 3.0 to 3.5 mm, just in the transitional arc of rail profile from R300 to R80 mm; the contact patch of S1002 profile generally slides, the contact stress of LMa profile is lowest, and the contact stress of XP55 profile is highest.So S1002 profile incompatibly matches Chinese 60 kg·m^-1 rail, the matching effect of XP55 profile is better, and the matching effect of LMa profile is best.
- vehicle engineering /
- wheel/rail profiles /
- rolling contact /
- wheel/rail relationship /
- vehicle/rail dynamics

HTML全文

图 1 轮对位移

Figure 1. Wheelset displacements

下载: 全尺寸图片幻灯片

图 2 轮对速度

Figure 2. Wheelset velocities

下载: 全尺寸图片幻灯片

图 3 接触点对

Figure 3. Contact points

下载: 全尺寸图片幻灯片

图 4 匹配关系对比

Figure 4. Comparison of matching relations

下载: 全尺寸图片幻灯片

图 5 蠕滑率

Figure 5. Creepages

下载: 全尺寸图片幻灯片

图 6 蠕滑力

Figure 6. Creep forces

下载: 全尺寸图片幻灯片

图 7 最大接触应力

Figure 7. Maximum contact stresses

下载: 全尺寸图片幻灯片

图 8 切向力分布

Figure 8. Tangent force distribution

下载: 全尺寸图片幻灯片

参考文献(10)

[1]	金学松, 沈志云. 轮轨滚动接触疲劳问题研究的最新进展[J]. 铁道学报, 2001, 23 (2): 92-108. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200102023.htm Jin Xue-song, Shen Zhi-yun. Rolling contact fatigue ofwheel/rail andits advanced research progress[J]. Journal ofthe China Rail way Society, 2001, 23 (2): 92-108. (in Chi-nese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200102023.htm
[2]	温泽峰, 金学松. 两种型面轮轨滚动接触蠕滑率/力的比较[J]. 工程力学, 2002, 19 (3): 82-89. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200203016.htm Wen Ze-feng, Jin Xue-song. Creepages and creep forces ofwheelset and track with two types of profiles in rolling con-tact[J]. Engineering Mechanics, 2002, 19 (3): 82-89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200203016.htm
[3]	金学松, 温泽峰, 张卫华. 两种型面轮轨滚动接触应力分析[J]. 机械工程学报, 2004, 40 (2): 5-11. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200402001.htm Jin Xue-song, Wen Ze-feng, Zhang Wei-hua. Analysis ofcontact stresses of wheel and rail with two types ofprofiles[J]. Chinese Journal of Mechanical Engineering, 2004, 40 (2): 5-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB200402001.htm
[4]	金学松, 温泽峰, 张卫华. 轮对运动状态对轮轨滚动接触应力的影响[J]. 工程力学, 2004, 20 (1): 165-173. doi: 10.3969/j.issn.1000-4750.2004.01.031 Jin Xue-song, Wen Ze-feng, Zhang Wei-hua. Effect ofwheelset motions on the rolling contact stresses of wheel andrail[J]. Engineering Mechanics, 2004, 20 (1): 165-173. (in Chinese) doi: 10.3969/j.issn.1000-4750.2004.01.031
[5]	温泽峰, 金学松, 刘兴奇. 两种型面轮轨滚动接触蠕滑率和摩擦功[J]. 摩擦学报, 2001, 21 (4): 288-292. https://www.cnki.com.cn/Article/CJFDTOTAL-MCXX200104010.htm Wen Ze-feng, Jin Xue-song, Liu Xing-qi. Creepages andfric-tion work of wheelset andtrack withtwo type profilesin roll-ing contact[J]. Tribology, 2001, 21 (4): 288-292. (in Chi-nese). https://www.cnki.com.cn/Article/CJFDTOTAL-MCXX200104010.htm
[6]	陈厚嫦, 黄体忠, 王群伟, 等. 轮对内侧距对机车车辆动力学性能影响的试验研究[J]. 中国铁道科学, 2006, 27 (5): 99-103. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200605018.htm Chen Hou-chang, Huang Ti-zhong, Wang Qun-wei, et al. Test study on the influence of the distance between backs of thewheel flanges on rolling stock s dynamic performance[J]. ChinaRail way Science, 2006, 27 (5): 99-103. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200605018.htm
[7]	孙善超, 王成国, 李海涛, 等. 轮/轨接触几何参数对高速客车动力学性能的影响[J]. 中国铁道科学, 2006, 27 (5): 93-98. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200605017.htm Sun Shan-chao, Wang Cheng-guo, Li Hai-tao, et al. Analy-sis of wheel/rail contact geometric parameters effect on thedynamic behavior of high-speed passenger car[J]. China Rail-way Science, 2006, 27 (5): 93-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200605017.htm
[8]	Zhai Wan-ming, Sun Xiang. A detailed model for investiga-ting vertical interactions between rail way vehicle andtrack[J]. Vehicle System Dynamics, 1994, 23 (S): 603-615.
[9]	金学松. 轮轨蠕滑理论及其试验研究[D]. 成都: 西南交通大学, 1999.
[10]	Kalker J J. Three-Dimensional Elastic Bodies in Rolling Contact[M]. Kluwer: Kluwer Academic Publishers, 1990.