Dynamic analysis of secondary suspension for low-speed maglev train
-
摘要: 分析了低速磁浮列车结构及其运动学关系, 利用多刚体动力学建模方法, 建立了低速磁浮列车的动力学模型, 分析了曲线通过时二系悬挂各构件的运动情况, 阐述了平行四边形机构在曲线通过中的重要作用。仿真结果表明: 二系悬挂系的平行四边形机构把横向力较平均地分配到各个模块上, 使得各个模块沿着曲线达到合理分布; 平行四边形机构减小了空气弹簧的横向力及纵向力, 减小了模块的摇头角, 有利于曲线通过与导向; 运行速度对滑台横移量有一定影响, 而轨道曲线半径是影响滑台滑动横移量的主要因素。Abstract: Low-speed maglev train structures and kinematical relationships were analyzed, its dynamics model was developed by using multi-rigid-body dynamics modeling method, the movements of different components of secondary suspension in curve negotiation were analyzed, and the significance of parallelogram mechanism in curve negotiation was explained. Simulation result shows that parallelogram mechanism averagely distributes lateral forces among modules, so that modules are distributed reasonably along the curve. Parallelogram mechanism decreases the lateral and longitudinal forces of air spring, and the yawing angles of modules, which is helpful for curve negotiation and guidance. Speed influences lateral displacement to a certain extent, while the curve radius of the track is the major factor.
-
0. 引言
随着低速磁浮列车技术的发展及其车辆动力学建模的日趋成熟, 低速磁浮线路曲线参数设计及磁浮车辆曲线通过性能研究也开展得越来越广泛。文献[1]探讨了长沙磁悬浮试验线定线参数; 文献[2-3]探讨了低速磁浮车辆转向机构的运动几何分析和几何曲线通过性; 文献[4]开展了高、低速磁浮车辆/轨道耦合动力学建模与仿真; 文献[5, 6, 7]]利用SIMPACK软件仿真、分析了高速磁浮车辆的静悬稳定性与动力性能; 文献[8]开展了低速磁浮车辆动态曲线通过性能研究; 文献[9]结合成都青城山磁浮列车试验示范线工程, 对低速磁浮车辆曲线通过动态响应进行分析, 并考虑电磁铁的主动悬浮与导向。但这些文献未从动力学角度考虑二系悬挂的平行四边形机构对磁浮列车曲线通过的影响。低速磁浮列车HSST100-L是日本作为运输工具原型车辆开发的, 车厢长14 m, 若不考虑二系悬挂的平行四边形机构在横向对车厢的影响, 建立的模型则不够完整。基于此, 本文建立了包括二系悬挂的整车动力学模型, 分析平行四边形机构对曲线通过的影响, 以及滑台在曲线通过时的横向滑动量。
1. 模型分析
1.1 基本原理
低速磁浮列车主要原理是基于EMS(Electromagnetic Suspension)悬浮和LSM(Linear Synchronous Motors)技术驱动。日本的HSST100-L型系列作为低速磁悬浮车辆的代表, 其主要原理是利用电磁铁的电磁吸力将列车悬浮在轨道上, 利用直线电机产生驱动力使车辆向前运行, 速度可以达到100~130 km·h-1, 悬浮气隙(Airgap)一般是8 mm, 每一个悬浮模块都有用于测量悬浮间隙的感应传感器。其垂向采用主动控制, 因为垂向的悬浮控制在没有反馈的情况下不稳定; 横向采用被动控制, 主要由二系悬挂上的空气弹簧提供阻尼。
1.2 二系悬挂结构分析
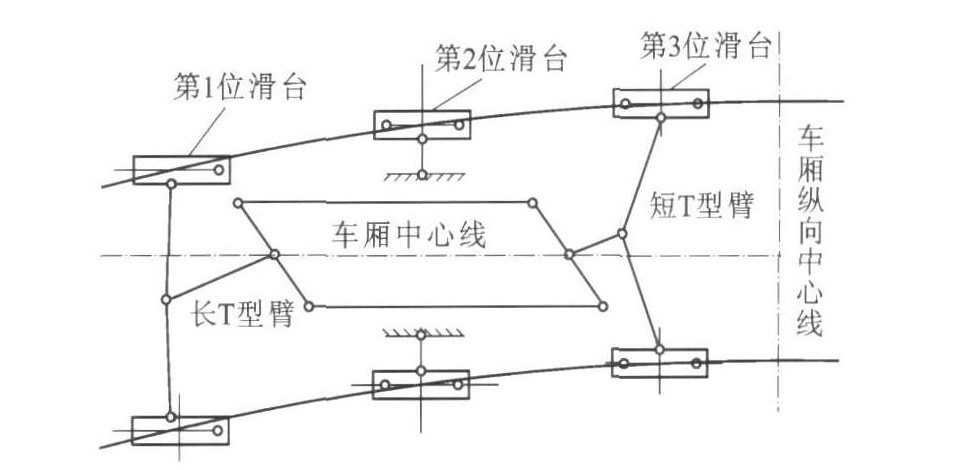
低速磁浮列车的车厢在自由滑台、固定滑台、空气弹簧和平行四边形机构等构成的二系悬挂上。二系悬挂具有运动解耦、减震和力的传递3个基本功能, 对车辆的运行性能和曲线通过能力具有重要的影响, 见图 1。走行机构和车厢的连接方式构成了车辆通过曲线的几何约束。
(1) 当车辆通过曲线时, 车辆的模块(每车5对)由于导向力作用, 将紧随线路排列成曲线形状。此时, 由于车厢为一个刚体, 不能随曲线弯曲, 各模块相对车厢将产生平移和转角, 由直线导轨副保证车厢和模块之间的平移量。
(2) 各个直线导轨副以及转臂和车体的销接点由于车厢的刚性, 纵向(弧长方向)距离不会变化。
(3) 第2、5位滑台横向于车厢刚性连接, 即在曲线上, 其左右滑台连线的中点始终是在车厢中心线上, 这2个中点其实构成了5个悬浮模块通过曲线的转动中心, 这是曲线通过动力学分析的基础。不管悬浮模块相对于曲线是什么样的形态(内接、外切、相交), 车厢中心线始终是第2、5位左右滑台中点的连线。
1.3 低速磁浮车辆模型
低速磁浮车辆模型由车厢、5对模块侧梁、4个固定滑台、8个滑台、2个长T型臂, 2个短T型臂、4个平行四边形机构拉杆和抗侧滚梁组成, 一系及二系悬挂的力用各自的弹簧阻尼力代替。本文假设各部件为刚体, 刚体的自由度见表 1。
表 1 自由度Table 1. Degrees of freedom
刚体的角速度为
ω=ωxi+ωyj+ωzk
刚体的速度为
v=vxi+vyj+vzk
刚体的动量为
L=mvxi+mvyj+mvzk
刚体的角动量为
Η=Ιxωxi+Ιyωyj+Ιzωzk
动量及角动量变化率为
dLdt=m˙vxi+m˙vyj+m˙vzk+ωL dΗdt=Ιx˙ωxi+Ιy˙ωyj+Ιz˙ωzk+ωΗ=[Ιx˙ωx+(Ιz-Ιy)ωyωz]i+[Ιy˙ωy+(Ιx-Ιz)ωxωz]j+[Ιz˙ωz+(Ιy-Ιx)ωyωx]k
式中: ωx、ωy、ωz分别为刚体关于x、y、z轴的角速度; vx、vy、vz为刚体的速度; Ix、Iy、Iz为刚体的转动贯量; m为刚体质量; i、j、k分别为x、y、z方向的单位矢量。
依据牛顿第二定律, 磁浮车辆系统动力学方程为
Μv¨Xv+Cv˙Xv+ΚvXv=Q
式中: Mv、Cv、Kv为车辆系统质量矩阵、阻尼矩阵和刚度矩阵; Q为车辆受到的外部力矢量; Xv为位移。
电磁铁与导轨横向中心对齐, 横向力Fy和垂向力Fz按照二维电磁力[10]解析式计算
Fy=Fm2cπWarctan(Yc)Fz=Fm[1+2cπW-2YπWarctan(Yc)]Fm=kf(i/c)2
式中: kf为电磁力常数; Y、c分别为电磁铁与导轨之间的横向位移与垂向间隙; W为磁极宽度; i为电流。
2. 曲线轨道
低速磁浮车辆的运行速度一般不高, 通过的曲线半径较小, 最小的曲线半径设置为R50 m, 在场线或库线工况, 最大通过速度为15 km·h-1, 无超高。R75 m曲线有6°超高设置, 缓和曲线长50 m, 以最大速度40 km·h-1安全通过。R100 m曲线有6°超高设置, 缓和曲线长50 m, 以最大速度60 km·h-1安全通过。仿真时采用德国高速低干扰不平顺作为激扰输入。
3. 动力学仿真及结果分析
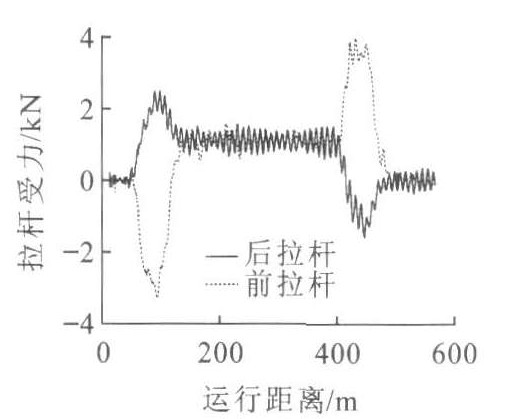
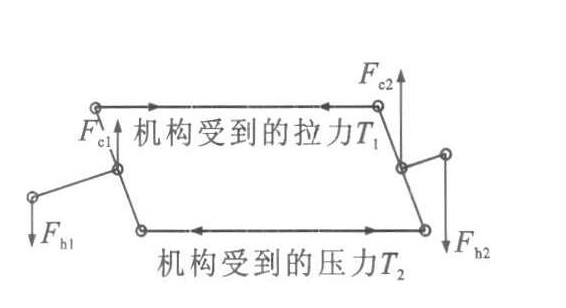
以40 km·h-1通过R100曲线时, 平行四边形机构的受力见图 2。磁浮车辆在直线段, 平行四边形机构杆件基本不受力; 在进出缓和曲线上, 平行四边形机构杆件受力较大, 最大约为3.5 kN; 在曲线上, 平行四边形机构杆件受力约为0.5 kN。由图 3的受力分析可知, 这些杆的内力是由车厢对四边形机构的横向力造成的, 所以平行四边形机构对曲线通过的影响有待于进一步分析。图 3中: Fhi为滑台对机构的力; Fci为车厢对机构的力; Ti为平行四边形机构杆的内力。
3.1 平行四边形机构对空气弹簧的影响
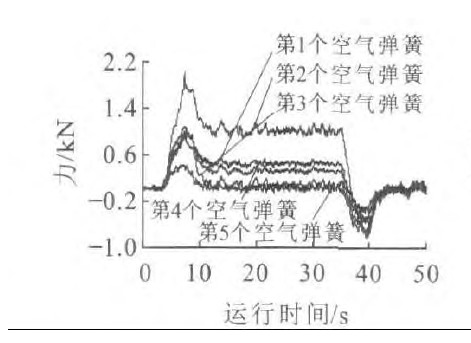
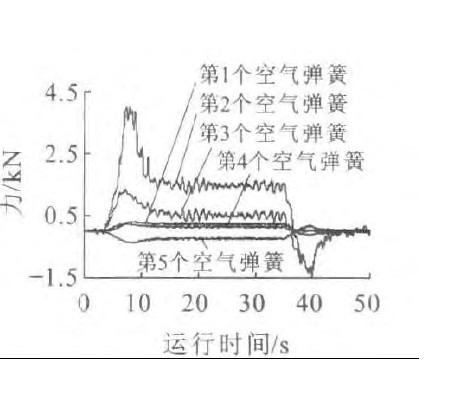
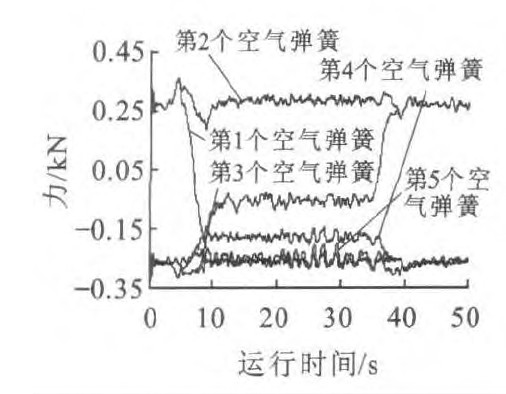
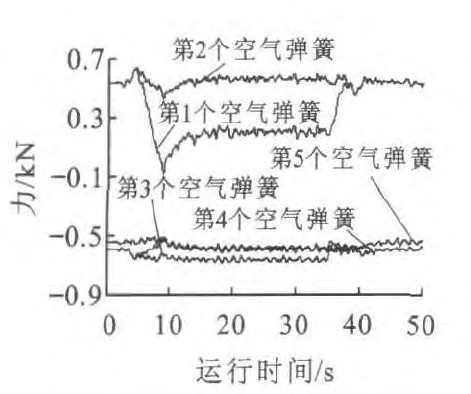
以日本的低速磁浮车辆HSST100-L为例, 每辆车有20个空气弹簧, 且空气弹簧的直径较小, 约230 mm, 因此, 能够减小车辆运行时空气弹簧在横向及纵向受力, 对空气弹簧性能稳定发挥, 提高寿命等十分有利。在曲线上, 由于欠超高、过超高或侧风的影响, 车厢将受到横向力, 横向力通过空气弹簧传到模块。图 4~7仅描述了磁浮车辆左边前5个空气弹簧在x向及y向的受力。比较图 4、5可知: 在直线段, 各个空气弹簧在y向受力约为0, 所以四边形机构对车辆在直线上运行时, 在y向没有约束, 即对y向没有影响; 在进出缓和曲线时, 空气弹簧受力达到最大, 最大的为第2个空气弹簧; 在曲线上, 各空气弹簧的受力比较稳定, 不同之处是, 有拉杆时, 第2个空气弹簧受力最大约为2 kN, 无拉杆时, 第2个空气弹簧受力最大约为4 kN, 是有拉杆时的2倍。比较图 6、7可知: 在x向空气弹簧受力均较小, 有拉杆时, x向力范围为-310~350 N, 无拉杆时, x向力范围为-700~650 N, 平行四边形机构使空气弹簧的受力减小一半。综上所述, 平行四边形机构使空气弹簧的受力重新分配, 受力较为均衡, 共同传递横向力。受力最大的空气弹簧(第2个空气弹簧)在y向受力减小了一半, 有利于横向力传递, 因此, 文献[11]的分析结论, 即平行四边形重要作用就是把横向力平均地分配到各个模块的悬挂系统上, 使所有的模块受力状态相同, 是不够合理的。
3.2 平行四边形机构对模块横移量的影响
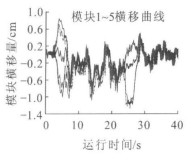
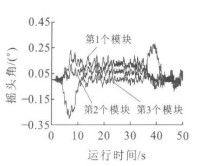
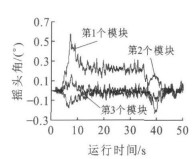
模块相对轨道横移量是一个体现车辆曲线通过能力的重要指标。对HSST原理的低速磁浮列车而言, 每个模块能获得最大的轨道重叠面积最有利于保持悬浮和导向能力。国内外的分析表明: 每个模块的最大横移量不能超过磁极宽度的一半, 如果车辆对应的磁极宽度取为28 mm, 则模块端部横向理论限位应为14 mm。图 8为模块中心相对轨道的横移曲线, 可以看出, 在曲线上, 横块的横移量较大, 达到了13 mm, 这是由欠超高造成的。模块的摇头角则是表现出模块与轨道的平行度, 虽然模块中心相对轨道的横移量不大, 如果摇头角太大, 也会使轨道与模块的重叠面积减小。当通过R100 m曲线时, 模块摇头角见图 9、10。在2种工况下, 摇头角相差较大, 有平行四边形机构时, 在缓和曲线上, 模块1和模块3的摇头角达到最大, 最大值为0.30°; 无平行四边形机构时, 在缓和曲线上, 模块1摇头角的增大最明显, 达到了0.58°, 是平行四边形机构的1.93倍。可见四边形机构使模块尽量与曲线一致, 获得最大的轨道重叠面积, 有利于保持悬浮和导向能力, 有利于车辆曲线通过。
3.3 通过R100 m曲线时二系悬挂系统各构件运动
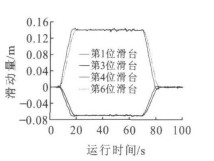
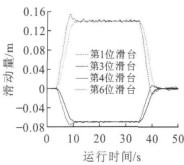
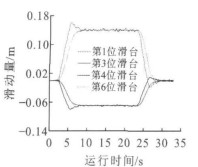
由图 11~13可知, 在曲线上, 第1、6位滑台的横向滑动量较大, 为143 mm, 第3、4位滑台的横向滑动量相对较小, 为72 mm, 是第1、6滑台滑动量的50%;在缓和曲线到曲线上时, 随着速度增大, 第1、3位滑台的横移量出现一个较小的波峰, 40 km·h-1时为12 mm, 60 km·h-1时为23 mm, 所以速度对滑台横移量也有一定的影响, 但不是很大。
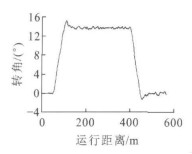
由于长T型臂、平行四边形拉杆和短T型臂构成了平行四边形, 所以长T型臂、短T型臂的转角相等。由图 14可知, 通过R100 m曲线时, 最大转角为14.2°。由1.2节的分析及图 15可知, 随着曲线半径的变小, 滑台的最大滑动位移将增大, 在R200曲线上时, 最大滑动位移只有80 mm, 而在R50曲线上, 最大滑动位移达到300 mm, 可见曲线半径是影响滑台的滑动位移的主要因素。由于T型臂与滑台通过横向拉杆铰接在一起, 转角也将随着曲线半径的变小而增大。
4. 结语
本文建立了5个模块的低速磁浮列车动力学模型, 共156个自由度。动力学分析结果表明: 二系悬挂系的平行四边形机构在曲线通过中起到重要作用, 把横向力较平均地分配到各个模块的悬挂系统上, 使所有的模块受力状态较为一致, 使得各个模块沿着曲线达到最合理分布。平行四边形机构使模块的摇头角减小, 从而使模块与轨道有较多的重叠面积, 有利于曲线通过与导向, 所以5个模块的低速磁浮车辆一定要有平行四边形机构或类似平行四边形的机构, 在动力学建模中就必须考虑平行四边形机构, 才能得到与实际较为一致的结果。在以40 km·h-1通过R100 m曲线时, 第1、6位滑台的横向滑动量为143 mm, 第3、4位滑台的横向滑动量为72 mm, 如果速度增大时, 滑动量有所增加, 60 km·h-1达到166 mm; T型臂的转角为14.2°。速度对滑台横移量也有一定的影响, 曲线半径是影响滑台滑动位移的主要因素, 在R50曲线时, 滑台滑动量达到了300 mm。本文的建模方法和分析结果对低速磁浮列车的设计和分析具有一定的参考价值。
-
表 1 自由度
Table 1. Degrees of freedom

-
[1] 张佩竹. 长沙磁悬浮试验线定线参数研究探讨[J]. 铁道工程学报, 2002(2): 6-10. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC200202002.htmZHANG Pei-zhu. Exploration on research of allocation parameters for Changsha maglev test track[J]. Journal of Rail way Engineering Society, 2002(2): 6-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC200202002.htm [2] 赵志苏, 尹力明, 罗昆. 磁浮列车转向机构运动分析与设计[J]. 机车电传动, 2000, 41(6): 11-13. https://www.cnki.com.cn/Article/CJFDTOTAL-JCDC200006003.htmZHAO Zhi-su, YI N Li-ming, LUO Kun. Motion analysis and design for yawing mechanismof maglev vehicle[J]. Electric Drive for Locomotives, 2000, 41(6): 11-13. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCDC200006003.htm [3] 曾佑文, 王少华. 三转向架磁悬浮车几何曲线通过分析[J]. 西南交通大学学报, 2003, 38(3): 282-285. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200303009.htmZENG You-wen, WANG Shao-hua. Research on geometrical curve negotiating of three-truck maglev vehicle[J]. Journal of Southwest Jiaotong University, 2003, 38(3): 282-285. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200303009.htm [4] 赵春发. 磁浮车辆系统动力学研究[D]. 成都: 西南交通大学, 2002. [5] 卜继玲, 付茂海, 严隽耄, 等. 常导吸引式低速磁悬浮车辆动态曲线通过性能研究[J]. 铁道学报, 2001, 23(1): 29-32. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200101005.htmBUJi-ling, FU Mao-hai, YAN Jun-mao. Study on dynamic performance of the low-speed EMS maglev car in curve negotiation[J]. Journal of the China Rail way Society, 2001, 23(1): 29-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200101005.htm [6] 邓永权. 磁浮列车静悬稳定性和仿真分析[D]. 成都: 西南交通大学, 2004. [7] 邓永权, 罗世辉, 梁红琴, 等. 基于SI MPACK的磁悬浮车辆耦合动力学性能仿真模型[J]. 交通运输工程学报, 2007, 7(1): 12-15. http://transport.chd.edu.cn/article/id/200701003DENG Yong-quan, LUO Shi-hui, LI ANG Hong-qin, et al. Si mulation model of maglev coupling dynamics performance based on SI MPACK[J]. Journal of Traffic and Transportation Engineering, 2007, 7(1): 12-15. (in Chinese) http://transport.chd.edu.cn/article/id/200701003 [8] 缪炳荣, 肖守讷, 罗世辉, 等. 磁悬浮车辆结构动力学建模与仿真[J]. 中国铁道科学, 2006, 27(1): 104-108. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200601020.htmMIAO Bing-rong, XIAOShou-ne, LUOShi-hui, et al. Modeling and si mulation of maglev vehicle structure dynamics[J]. China Railway Science, 2006, 27(1): 104-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200601020.htm [9] 赵春发, 翟婉明, 王其昌. 低速磁浮车辆曲线通过动态响应仿真分析[J]. 中国铁道科学, 2005, 26(3), 94-98. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200503020.htmZHAO Chun-fa, ZHAI Wan-ming, WANG Qi-chang. Si mu-lation analysis of the dynamic response of low-speed maglev vehicle curve negotiation[J]. China Rail way Science, 2005, 26(3): 94-98. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200503020.htm [10] BREZI NA W, LANGERHOLC J. Lift and side force on rectangular pole pieces in two di mensions[J]. Journal of Applied Physics, 1974, 45(4): 1869-1872. [11] 蒋海波, 罗世辉, 董仲美, 等. 低速磁浮列车迫导向机构的研究[J]. 内燃机车, 2007(4): 15-17. https://www.cnki.com.cn/Article/CJFDTOTAL-LRJX200704003.htmJI AN Hai-bo, LUO Shi-hui, DONG Zhong-mei, et al. Study of forced steering mechanism of low-speed maglev train[J]. Diesel Locomotives, 2007(4): 15-17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LRJX200704003.htm -






 下载:
下载:














 下载:
下载: