Comprehensive-model method of reliability analysis for traffic accident reconstruction with redundant information
-
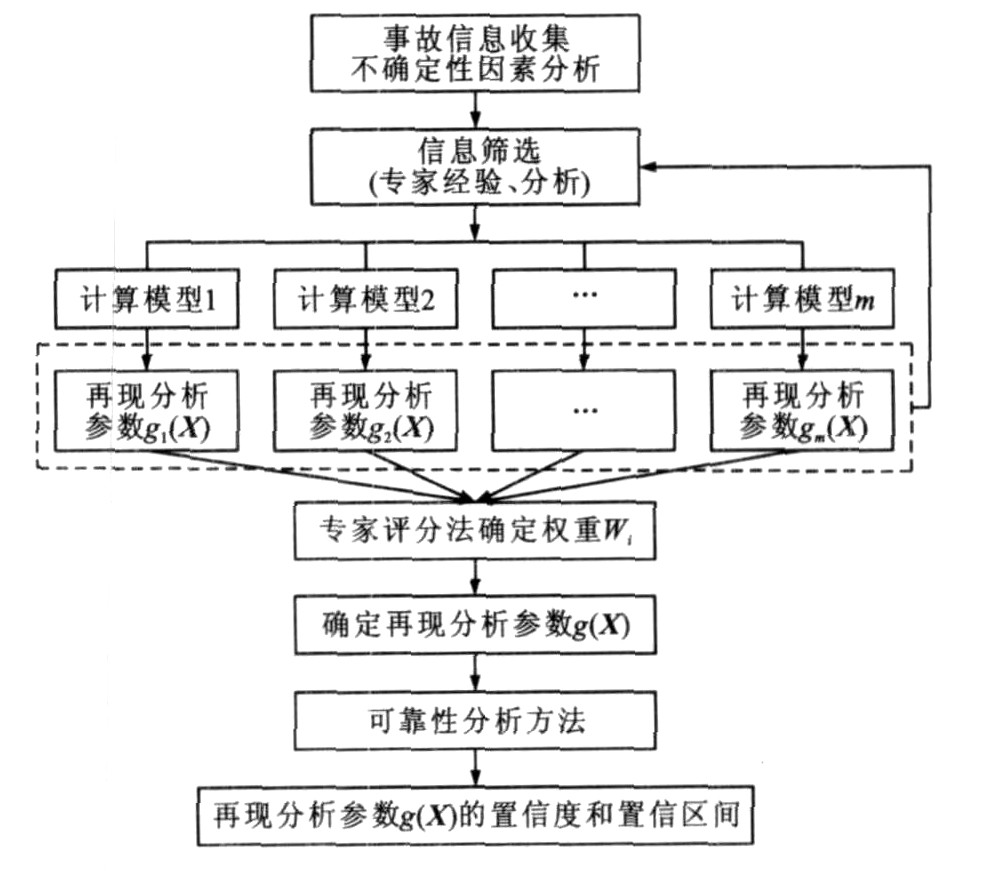
摘要: 为了评价交通事故再现分析结果的可信性, 将高阶矩技术、随机摄动法和Edgeworth级数与交通事故再现分析技术相结合, 提出了交通事故再现可靠性分析方法, 给出了再现分析结果的置信度和置信区间。针对具有冗余信息的交通事故再现分析, 应用主观赋权法、可靠性分析技术和优化求解技术, 提出了冗余信息交通事故再现可靠性分析的综合模型法。最后通过实际交通事故案例进行了事故再现分析。研究结果表明: 该方法在考虑各基本因素客观不确定性的基础上同时结合了专家经验, 与各基本再现分析模型计算结果相比, 其均值趋于各基本再现分析模型的中间值, 其变化范围(标准差) 最小, 再现分析结果更具科学性和准确性。Abstract: In order to estimate the creditability of traffic accident reconstruction analysis, a reconstruction reliability analysis method was put forward which combined high-order moment technology, probabilistic perturbation method, Edgeworth series and reconstruction analysis technology.The confidence interval and confidence of reconstruction analysis result were obtained as the estimate indexes of the creditability.For traffic accident reconstruction reliability analysis with redundant information, a comprehensive-model method was proposed through integrating subjective weighting method, reliability analysis technology and optimization technology.A practical traffic accident case was investigated to verify the method's feasibility and validity.Study result indicates that the mean calculated by comprehensive-model method tends to the intermediate value of basic reconstruction analysis models, and the change range is minimum.So the reconstruction analysis result is more precise and scientific by using comprehensive-model method because of considering the intrinsical uncertainty influence of basic factors and expert experiences.
-
表 1 基本随机参数及其统计特征值
Table 1. Basic random parameters and statistic eigenvalues
随机参数 均值 标准差 三阶中心矩 四阶中心矩 Lcz/m 12.80 0.12 0 6.40×10-4 Lzh/m 13.65 0.16 0 1.82×10-3 Lrp/m 20.40 0.23 0 8.99×10-3 Lrc/m 12.40 0.23 0 9.18×10-3 Lsp/m 12.26 0.31 0 2.77×10-2 Lsz/m 19.43 0.31 0 2.84×10-2 Lsk/m 14.34 0.31 0 2.95×10-2 h/m 1.04 0.03 0 2.61×10-6 μcz 0.65 0.04 0 6.84×10-6 μzh 0.53 0.02 0 9.33×10-7 μrc 0.50 0.04 0 6.96×10-6 表 2 车辆行驶速度的统计特征值
Table 2. Statistic eigenvalues of vehicle speeds
行驶速度/ (km·h-1) 均值/ (km·h-1) 标准差/ (km·h-1) 三阶中心矩/ (km·h-1)3 四阶中心矩/ (km·h-1)4 偏态系数 峰态系数 Vc1 47.95 1.46 0.00 13.57 0.00 3.00 Vc2 44.72 1.03 0.00 3.40 0.00 3.04 Vc3 45.28 1.53 0.00 16.57 0.00 3.05 Vc4 41.39 1.67 0.00 23.24 0.00 3.02 Vc5 43.21 1.04 0.00 3.48 0.00 3.03 Vc6 39.42 0.71 0.00 0.75 0.00 2.98 Vc7 44.11 1.33 0.00 9.60 0.00 3.06 Vc 44.07 0.60 0.00 0.38 0.00 2.99 -
[1] 张雷, 李一兵. 道路交通事故再现分析结果的不确定性分析[J]. 公路交通科技, 2007, 24 (12): 140-143. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200712032.htmZHANG Lei, LI Yi-bing. Analysis of traffic accident recon-struction uncertainty[J]. Journal of Highway and Transpor-tation Research and Development, 2007, 24 (12): 140-143. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200712032.htm [2] 李一兵, 袁泉, 陈理. 车辆碰撞行人交通事故的不确定因素研究[J]. 中国公路学报, 2004, 17 (1): 82-85. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200401020.htmLI Yi-bing, YUAN Quan, CHENLi. Study of uncertainfactorsin traffic accidents of vehicle i mpacting pedestrian[J]. ChinaJournal of Highway and Transport, 2004, 17 (1): 82-85. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200401020.htm [3] 刘成, 李一兵, 袁泉, 等. 基于完全信息的车速建模及Moore-Penrose广义逆求解[J]. 汽车工程, 2003, 25 (6): 621-624, 629. doi: 10.3321/j.issn:1000-680X.2003.06.024LIU Cheng, LI Yi-bing, YUAN Quan, et al. A vehicle speedmodel based on complete information and its solution bythe methodof Moore-Penrose generalized matrix inverse[J]. AutomotiveEngineering, 2003, 25 (6): 621-624, 629. (in Chinese) doi: 10.3321/j.issn:1000-680X.2003.06.024 [4] 许洪国, 李世武, 施树明, 等. 推算交通事故汽车碰撞速度的综合约束方法[J]. 中国安全科学学报, 1998, 8 (3): 60-64. https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK199803013.htmXU Hong-guo, LI Shi-wu, SHI Shu-ming, et al. Compre-hensive restraint method for esti mating the crash speed ofmotor vehicle at traffic accident[J]. China Safety ScienceJournal, 1998, 8 (3): 60-64. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZAQK199803013.htm [5] 张义民, 张雷. 结构系统可靠性优化设计的神经网络方法[J]. 计算力学学报, 2005, 22 (3): 257-261. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200503001.htmZHANG Yi-min, ZHANG Lei. Reliability-based structuralopti mization using neural network[J]. Chinese Journal ofComputational Mechanics, 2005, 22 (3): 257-261. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200503001.htm [6] 张义民, 张雷. 基于神经网络的结构可靠性优化设计[J]. 应用力学学报, 2005, 22 (1): 49-54. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX20050100A.htmZHANG Yi-min, ZHANG Lei. Structural reliability opti mumdesign based on MCS-NN method[J]. Chinese Journal ofApplied Mechanics, 2005, 22 (1): 49-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX20050100A.htm [7] 张艳, 马川生, 韦可. 组合预测种权重的确定研究[J]. 交通运输系统工程与信息, 2006, 6 (4): 125-129. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT200604024.htmZHANG Yan, MAChuan-sheng, WEI Ke. The study of esti ma-tion of weight coefficient in combination forecast models[J]. Journal of Transportation Systems Engineering and Informa-tion Technology, 2006, 6 (4): 125-129. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT200604024.htm [8] 王中兴, 李桥兴. 依据主、客观权重集成最终权重的一种方法[J]. 应用数学与计算数学学报, 2006, 20 (1): 87-92. https://www.cnki.com.cn/Article/CJFDTOTAL-YONG200601013.htmWANG Zhong-xing, LI Qiao-xing. An approach to integratethe final weights based on the subjective and objectiveweightsm[J]. Communication on Applied Mathematics andComputation, 2006, 20 (1): 87-92. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YONG200601013.htm -





 下载:
下载: