Practical evaluation method of component reliability for existing concrete bridge
-
摘要: 为了实现对在役混凝土桥梁构件可靠性的快速评估, 建立了考虑活载影响修正系数及评估基准期影响的汽车荷载效应概率模型, 给出了基于抗力分项系数和界限系数的在役混凝土桥梁构件承载力等级的评定标准。以构件的受力状态、抗力损伤程度、汽车荷载效应与恒载效应之比及评估基准期4个主要因素为依据, 通过大量运算提出了在役桥梁构件承载能力可靠性评估方法。依据《公路工程结构可靠度设计统一标准》(GB/T50283—1999)中的方法求得一座在役桥梁可靠指标为4.21, 对应结构安全等级为二级; 采用本文方法得到检算指标为0.994, 评价结果为二类, 与规范评定的结果接近, 表明该方法简便、可行。Abstract: In order to realize the rapid assessment of the reliability of existing concrete bridge, a loading effect probability model considering evaluation base period and the modification factor of live load was established.A classification evaluation criterion of component's bearing capacity was put forward, which regarded resistance coefficients and limit coefficients.Four main factors were taken into account, which are the bearing force situation, the determination degree of resistance, the ratio of vehicle load to dead load and the assessment reference period.A practical evaluation method of reliability for existing concrete bridge's component was put forward through a lot of reliability calculation.For an existing concrete bridge, the reliability index is 4.21 and the safety grade is secondary according to the computation method from unified standard for reliability design of highway engineering structures(GB/T 50283—1999).The checking index is 0.994 and the assessment result is also secondary.Computation result indicates that the method is convenient and practical.
-
Key words:
- bridge engineering /
- existing concrete bridge /
- bearing capacity /
- reliability evaluation
-
图 1 分项系数与活、恒载效应比的关系曲线
Figure 1. Curves of partial coefficients and ratio of vehicle load to dead load
图 2 界限系数与活、恒载效应比的关系曲线
Figure 2. Curves of limit coefficients and ratio of vehicle load to dead load
表 1 汽车荷载效应统计参数
Table 1. Statistical parameters of vehicle action effect
汽车运行状态 效应种类 统计参数 κSQ, T δSQ, T 一般运行状态 弯矩 0.686 1 0.156 9 剪力 0.608 3 0.158 1 密集运行状态 弯矩 0.799 5 0.086 2 剪力 0.718 7 0.076 9 
下载: 导出CSV
表 2 汽车荷载效应的概率分布函数
Table 2. Probability distribution functions of vehicle action effect
汽车运行状态 效应种类 概率分布函数 一般运行状态 弯矩 F1(x, T1)=exp 剪力 F2(x, T1)=exp 密集运行状态 弯矩 F3(x, T1)=exp 剪力 F4(x, T1)=exp
下载: 导出CSV
表 3 考虑评估基准期影响的活载效应修正系数
Table 3. Modified coefficients of live load effect considering assessment reference period
T1/年 一般运行状态 密集运行状态 弯矩 剪力 弯矩 剪力 10 0.782 0 0.780 7 0.866 7 0.879 3 20 0.847 6 0.846 8 0.906 9 0.915 6 30 0.886 0 0.885 3 0.930 3 0.936 8 40 0.913 2 0.912 8 0.947 0 0.951 9 50 0.934 4 0.934 0 0.959 9 0.963 6 60 0.951 6 0.951 4 0.970 5 0.973 2 70 0.966 3 0.966 0 0.979 3 0.981 3 80 0.978 9 0.978 7 0.987 1 0.988 3 90 0.990 1 0.989 8 0.993 9 0.994 5 100 1.000 0 1.000 0 1.000 0 1.000 0
下载: 导出CSV
表 4 构件抗力计算模式统计参数
Table 4. Statistical parameters of calculation model for resistance of structural members
受力状态 μΩP δΩP 正截面受弯 1.098 0 0.071 0 斜截面受剪 矩形截面 1.486 1 0.283 2 T形截面① 1.901 1 0.088 4 偏心受压(短柱) 矩形截面 大偏心 1.065 0 0.088 0 小偏心 1.070 0 0.095 0 圆形截面② 0.991 2 0.258 8 注: ①考虑T形截面受压翼缘的影响系数α3 =1.1, 经计算确定; ②根据新规范对135根圆形截面偏心受压构件的统计计算, 试验值/新规范简化计算值的均值为0.991 2, 变异系数为0.258 8。
下载: 导出CSV
表 5 构件抗力的统计参数
Table 5. Statistical parameters for resistance of structural members
受力状态 κR δR 正截面受弯 1.098 0 0.122 6 斜截面受剪 矩形截面 1.486 1 0.300 3 T形截面 1.901 1 0.133 5 偏心受压(短柱) 矩形截面 大偏心 1.065 0 0.133 2 小偏心 1.070 0 0.137 9 圆形截面 0.991 2 0.277 4 注: κR为考虑ΩP与Ωt综合效应的统计参数。
下载: 导出CSV
表 6 基于可靠指标的分级原则
Table 6. Grading principle based on reliability index
破坏形式 一类 二类 三类 四类 五类 延性破坏 β≥4.20 4.20 > β≥3.95 3.95 > β≥3.70 3.70 > β≥2.95 2.95 > β 脆性破坏 β≥4.70 4.70 > β≥4.45 4.45 > β≥4.20 4.20 > β≥3.45 3.45 > β
下载: 导出CSV
表 7 分项系数及界限系数值
Table 7. Partial coefficients and limit coefficients
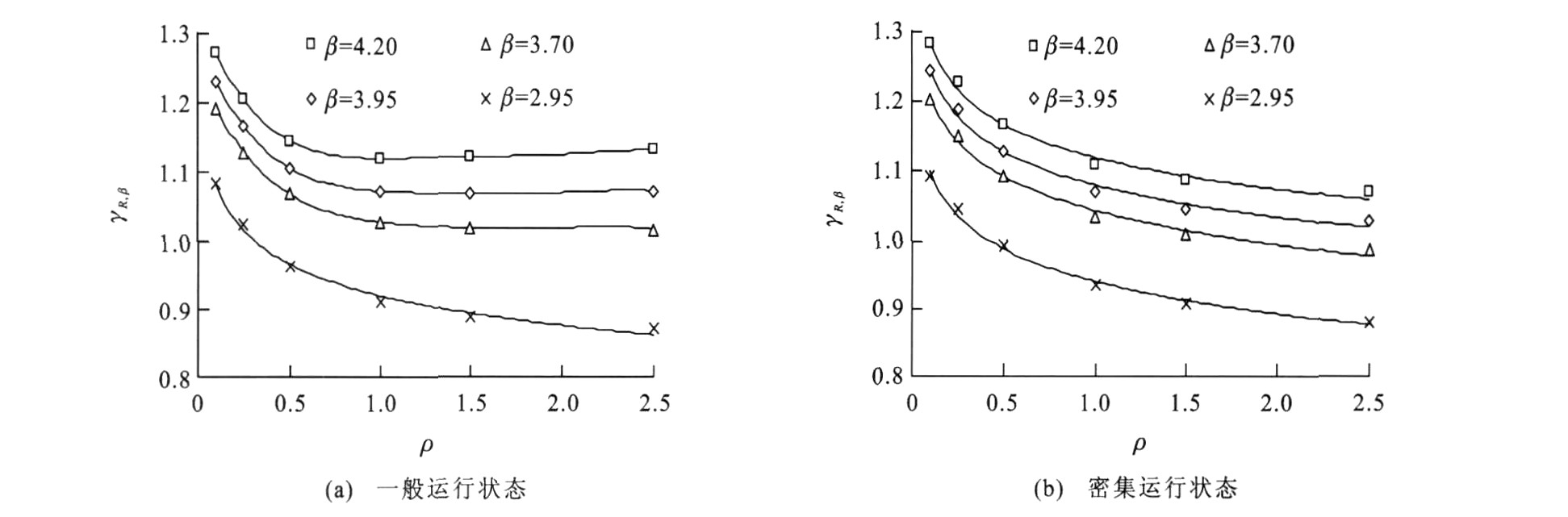
汽车运行状态 ρ γR, 4.20 γR, 3.95 γR, 3.70 γR, 2.95 b c d 一般运行状态 0.10 1.271 5 1.231 2 1.192 3 1.082 8 0.968 0.938 0.852 0.25 1.204 5 1.166 1 1.129 0 1.024 5 0.968 0.937 0.851 0.50 1.145 5 1.106 0 1.068 3 0.964 2 0.966 0.933 0.842 1.00 1.120 4 1.073 0 1.028 5 0.910 5 0.958 0.918 0.813 1.50 1.122 6 1.069 5 1.019 9 0.889 4 0.953 0.909 0.792 2.50 1.132 5 1.072 9 1.017 2 0.871 8 0.947 0.898 0.770 密集运行状态 0.10 1.283 9 1.243 4 1.204 1 1.093 8 0.968 0.938 0.852 0.25 1.227 3 1.188 7 1.151 3 1.046 1 0.969 0.938 0.852 0.50 1.166 5 1.129 5 1.093 6 0.993 0 0.968 0.938 0.851 1.00 1.108 5 1.070 9 1.035 0 0.935 7 0.966 0.934 0.844 1.50 1.086 5 1.046 8 1.009 1 0.907 0 0.963 0.929 0.835 2.50 1.071 5 1.028 4 0.987 7 0.879 6 0.960 0.922 0.821
下载: 导出CSV
表 8 界限系数
Table 8. Limit coefficients
界限系数 正截面受弯 斜截面受剪 偏心受压(短柱) 矩形截面 T形截面 矩形截面 圆形截面 大偏心 小偏心 b 0.96 0.93 0.96 0.96 0.96 0.93 c 0.93 0.86 0.92 0.92 0.92 0.87 d 0.83 0.69 0.82 0.82 0.82 0.70
下载: 导出CSV
表 9 承载能力评定标准
Table 9. Evaluation standard of bearing capacity
构件承载力等级 可靠性要求 检算标准 处治措施 一类 构件承载力满足目标可靠性要求 R/(γ0γRS)≥1 不必采取处治措施 二类 构件承载力略低于目标可靠性要求 b≤R/(γ0γRS) < 1 需小修, 不需加固 三类 构件承载力仅能满足最低可靠性要求 c≤R/(γ0γRS) < b 需中修, 不需加固 四类 构件承载力低于最低可靠性要求 d≤R/(γ0γRS) < c 特殊检查后大修或加固 五类 构件承载力大大低于最低可靠性要求 R/(γ0γRS) < d 特殊检查后确定处治对策
下载: 导出CSV
表 10 分项系数
Table 10. Partial coefficients
汽车运行状态 ρ γR 正截面受弯 斜截面受剪 偏心受压(短柱) 矩形截面 T形截面 矩形截面 圆形截面 大偏心 小偏心 一般运行状态 0.10 1.271 5 2.270 4 0.817 1 1.368 8 1.491 6 3.081 6 0.25 1.204 5 2.126 4 0.766 4 1.296 4 1.413 4 2.914 3 0.50 1.145 5 1.965 4 0.717 5 1.229 1 1.345 2 2.732 4 1.00 1.120 4 1.792 9 0.689 4 1.193 7 1.323 3 2.552 3 1.50 1.122 6 1.710 1 0.685 9 1.192 2 1.333 1 2.477 4 2.50 1.132 5 1.637 4 0.688 0 1.199 2 1.353 7 2.423 0 密集运行状态 0.10 1.283 9 2.293 9 0.825 0 1.382 3 1.506 2 3.113 6 0.25 1.227 3 2.174 4 0.781 0 1.321 5 1.439 9 2.979 4 0.50 1.166 5 2.036 8 0.731 7 1.255 5 1.368 8 2.826 7 1.00 1.108 5 1.877 6 0.679 2 1.190 1 1.301 3 2.656 1 1.50 1.086 5 1.789 6 0.654 6 1.163 3 1.277 3 2.565 5 2.50 1.071 5 1.696 4 0.634 1 1.143 4 1.263 1 2.474 4
下载: 导出CSV
-
[1] 顾祥林, 许勇, 张伟平. 既有建筑结构构件的安全性分析[J]. 建筑结构学报, 2004, 25(6): 117-122. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB200406018.htmGU Xiang-lin, XU Yong, ZHANG Wei-ping. Safety analysis of structural members of existing buildings[J]. Journal of Building Structures, 2004, 25(6): 117-122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB200406018.htm [2] 贺拴海, 吕颖钊. 考虑材料耐久性的在役混凝土结构可靠度研究[J]. 建筑科学与工程学报, 2005, 22(1): 71-75, 82. https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG200501012.htmHE Shuan-hai, LU Ying-zhao. Reliability research of existing reinforced concrete structures[J]. Journal of Architecture and Civil Engineering, 2005, 22(1): 71-75, 82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XBJG200501012.htm [3] 欧进萍, 刘学东, 王光远. 现役结构安全度评估的环境荷载标准研究[J]. 工业建筑, 1995, 25(8): 11-16, 35. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ508.002.htmOUJin-ping, LI U Xue-dong, WANG Guang-yuan. Study onthe environmental load criteria of existing structure safety evaluation[J]. Industrial Construction, 1995, 25(8): 11-16, 35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ508.002.htm [4] ALLEN D E. Li mit states criteria for structural evaluation of existing buildings[J]. Canadian Journal of Civil Engineering, 1991, 18(6): 995-1004. doi: 10.1139/l91-122 [5] SZERSZEN M M, SZWED A, NOWAK A S. Reliability analysis for eccentrically loaded columns[J]. Structural Journal, 2005, 102(5): 676-688. [6] 岑国平, 李明锋. 机场跑道长度可靠性设计方法[J]. 交通运输工程学报, 2004, 4(1): 62-65. http://transport.chd.edu.cn/article/id/200401016CEN Guo-ping, LI Ming-feng. Reliability design method of airport runwaylength[J]. Journal of Traffic and Transporta-tion Engineering, 2004, 4(1): 62-65. (in Chinese) http://transport.chd.edu.cn/article/id/200401016 [7] 周建方, 周美英, 李典庆. 现役钢闸门结构最低可靠度标准的确定[J]. 中国农村水利水电, 2003(5): 48-51. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200305024.htmZHOU Jian-fang, ZHOU Mei-ying, LI Dian-qing. Deter-mining lowest dependability standard for steel gate structure currently in use[J]. China Rural Water and Hydropower, 2003(5): 48-51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNSD200305024.htm [8] ESTES A C, ASCE M, FRANGOPOL D M, et al. Load rating versus reliability analysis[J]. Journal of Structural Engineering, 2005, 131(5): 843-847. [9] 吕颖钊, 贺拴海. 缺损钢筋混凝土梁桥模糊可靠性评价模型[J]. 交通运输工程学报, 2005, 5(4): 58-62. http://transport.chd.edu.cn/article/id/200504012LU Ying-zhao, HE Shuan-hai. Fuzzy reliability evaluation of defective RC beambridge[J]. Journal of Traffic and Trans-portation Engineering, 2005, 5(4): 58-62. (in Chinese) http://transport.chd.edu.cn/article/id/200504012 -
点击查看大图
计量
- 文章访问数: 982
- HTML全文浏览量: 194
- PDF下载量: 775
- 被引次数: 0
