Hunting motion and bifurcation behavior of six-axle locomotive based on continuation method
Article Text (Baidu Translation)
-
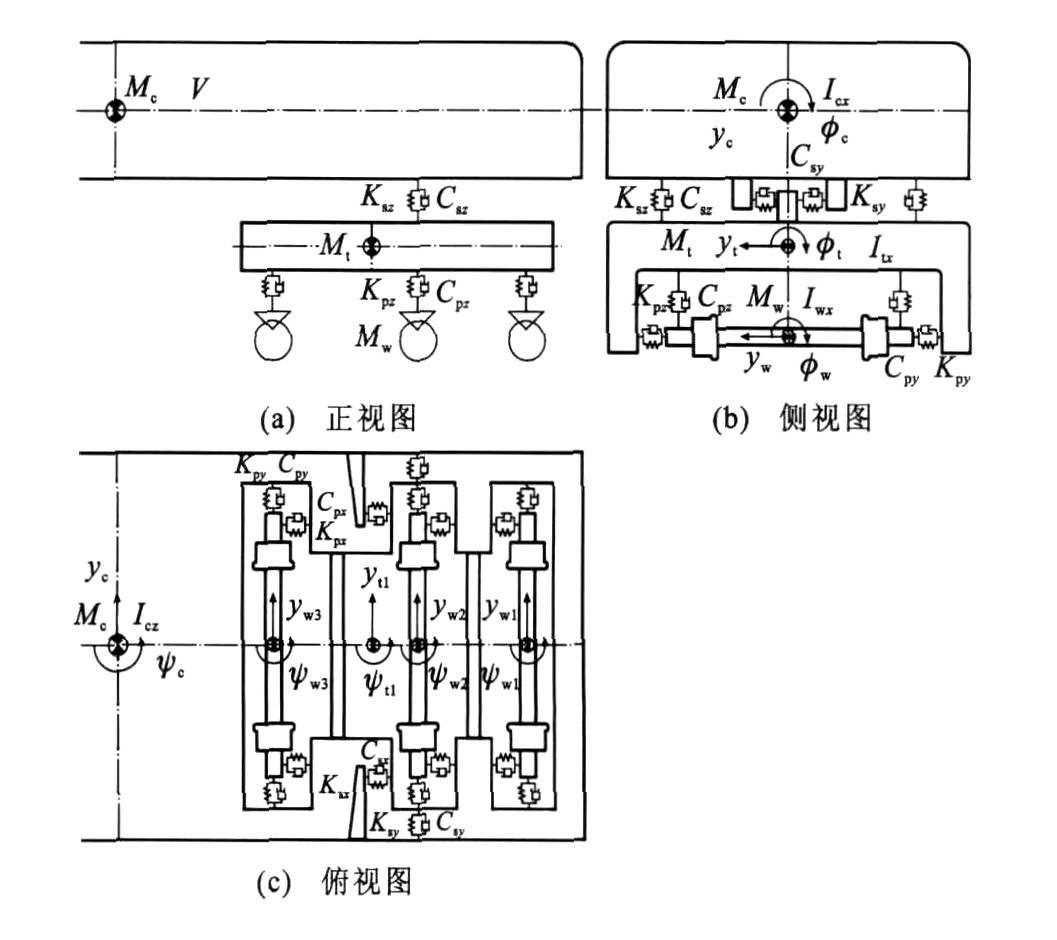
摘要: 以六轴机车系统为研究对象, 采用Vermeulen-Johnson蠕滑理论和一分段线性函数分别计算轮轨滚动接触蠕滑力和轮缘力, 研究了机车系统运行于理想平直轨道上的蛇形运动分岔问题。将基于切向量进行预测、牛顿迭代进行校正、可逐步求解整个系统解分支曲线的延续算法应用于机车系统的Hopf分岔及周期解的追踪和求解。计算结果表明: 车辆系统在速度达到53.700m.s-1时, 从稳定的定常解分岔出一不稳定的周期解, 该周期解在速度降到50.855m.s-1时又恢复了稳定, 在此过程中出现的亚临界Hopf分岔会引起系统摆振幅值出现突跳与迟滞现象; 在低速及高速情况下的一些速度区间, 机车系统都有可能出现多种摆振形式共存的非线性动力学现象。Abstract: A six-axle locomotive with simple nonlinearities was taken as the study object.The creep forces and the flange forces between wheels and rails in rolling contact were decided by the Vermeulen-Johnson creep force laws and piecewise function respectively.The hunting motion and bifurcation behavior of the locomotive running on ideal straight and perfect track were analyzed in detail.Based on tangent predictor, Newton iteration corrector and computing the entire solution branches step by step, a continuation algorithm was presented to calculate and track the limit cycles in the locomotive system.It is pointed out that an unstable periodic solution is bifurcated from a stable stationary solution when vehicle speed reaches 53.700 m·s-1, while the unstable periodic solution remains its stability when the speed reduces to 50.855 m·s-1.In the processes, the subcritical Hopf bifurcation can cause the jump and hysteretic phenomena of the oscillating amplitude.The result indicates that such nonlinear phenomena as the coexistence of some oscillations may appear in some either low or high speed range of the locomotive.
-
图 2 1位轮对最大横向位移分岔
Figure 2. Bifurcation of the maximal lateral displacement of leading wheelset
-
[1] KNOTHE K, B HM F. History of stability of rail way and road vehicles[J]. Vehicle System Dynamics, 1999, 31(5): 283-323. [2] MOHAN A. Nonlinear investigation of the use of controllable pri mary suspensions to i mprove hunting in railway vehicles[D]. Blacksburg: Virginia Polytechnic Institute and State University, 2003. [3] WICKENS A H. The dynamic stability of rail way vehicle wheelsets and bogies having profiled wheels[J]. International Journal of Solids and Structures, 1965, 1: 319-341. doi: 10.1016/0020-7683(65)90037-5 [4] KAAS-PETERSEN C. Chaos in a rail way bogie[J]. Acta Mechanica, 1986, 61: 89-107. doi: 10.1007/BF01176365 [5] TRVE H. Railway vehicle chaos and asymmetric hunting[J]. Vehicle System Dynamics, 1992, 20(6): 625-637. [6] 曾京. 车辆系统的蛇形运动分叉及极限环的数值计算[J]. 铁道学报, 1996, 18(3): 13-19. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB603.002.htmZENGJing. Numerical computations of the hunting bifurca-tion and li mit cycles for rail way vehicle system[J]. Journal of the China Railway Society, 1996, 18(3), 13-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB603.002.htm [7] AHMADI AN M, YANG S. Effect of system nonlinearities on locomotive bogie hunting stability[J]. Vehicle System Dynamics, 1998, 29(6): 365-384. [8] 司道林, 王开云, 翟婉明, 等. 牵引力对机车横向运动稳定性的影响[J]. 交通运输工程学报, 2009, 9(1): 21-24. http://transport.chd.edu.cn/article/id/200901005SI Dao-lin, WANG Kai-yun, ZHAI Wan-ming, et al. Effect of traction force onlateral stability of locomotive[J]. Journal of Traffic and Transportation Engineering, 2009, 9(1): 21-24. (in Chinese) http://transport.chd.edu.cn/article/id/200901005 [9] VERMEULEN P J, JOHNSON K L. Contact of nonspherical elastic bodies transmitting tangential forces[J]. Journal of Applied Mechanics, 1964, 31: 338-340. [10] BRI NDLEY J, KAAS-PETERSEN C, SPENCE A. Path-following methods in bifurcation problems[J]. Physica D: Nonlinear Phenomena, 1989, 34(3): 456-461. [11] DOEDEL E J. Continuation and bifurcation software for ordin-ary differential equations[R]. Montreal: Concordia University, 2008. [12] HUANG Cheng-rong, ZHAN Fei-sheng. The numerical bifurcation method of nonlinear lateral stability analysis of a locomotive[J]. Vehicle System Dynamics, 1994, 23(1): 234-245. -
下载:
点击查看大图
图(4)
计量
- 文章访问数: 700
- HTML全文浏览量: 140
- PDF下载量: 490
- 被引次数: 0
