Dynamic response properties of two-way subgrade in bridge-subgrade transition section under moving load
-
摘要: 采用有限元方法, 建立了重载铁路路桥过渡段双线路基整体三维模型, 分析了动荷载作用下双线路基动力响应规律。研究发现: 相向移动荷载作用下路基横向上各点的位移曲线呈“W”形状, 路基左右两侧荷载作用面积中心下的位移最大; 路基左侧最大位移要大于右侧最大位移, 点离荷载中心越近, 该点位移波动变化越剧烈。结果表明: 荷载除对其作用一侧的路基位移有影响外, 又加剧了路基另一侧位移; 沿深度方向, 荷载对路基位移的影响逐渐减弱。Abstract: A 3D finite-element model was established by using finite element method to systematically study the dynamic response characteristics of subgrade in bridge-subgrade transition section of heavy haul railway under dynamic load.The response rules were summarized after analysis.It is pointed that the displacement curves of the points in horizontal direction of subgrade are assumed W shape under moving towards load.The displacement of the point at the center of loading area is largest, and the maximum displacement on the left of subgrade is larger than that on the right.More close to the loading center, the displacement change of the point is more dramatic.The result indicates that the load not only has impact on the displacements of the points on its action side, but also exacerbates the ones on the other side.Along the depth direction, the impact of load on subgrade displacement wears off.
-
Key words:
- heavy haul railway /
- bridge-subgrade transition section /
- subgrade /
- dynamic response /
- 3D FEM
-
0. 引言
Shamsabadi建立了路桥过渡段的三维连续有限元模型, 并进行了动力分析, 但其模型中过渡段路基采用非线性弹簧模拟, 计算结果不符合实际[1]; 罗强全面分析了不同行车速度与车辆进出过渡段等情况对动力学性能指标的影响规律[2]; 陶向华建立了路桥过渡段三维有限元模型, 模拟车辆动荷载作用下路基和地基土的变形特性[3]; 张洪亮根据路桥过渡段的实际差异沉降图式分别确定了不设和设搭板的路桥过渡段计算模型[4]; 李献民对高速铁路加筋过渡段进行了静动力特性分析, 并提出了过渡段车辆平稳舒适性的动力学控制指标[5]。以上研究主要针对高速公路或铁路, 而对于重载铁路, 随着列车轴载和速度的增加, 使路基的变形和动力响应加剧, 目前对这方面的研究还不够完善。基于此, 本文对重载条件下路桥过渡段路基的动力响应规律进行探讨, 通过建立路桥过渡段双线路基三维有限元模型, 模拟朔黄铁路试验现场双线条件下, 列车相向而行情况下路桥过渡段路基的动力响应, 并进一步分析过渡段路基不同横断面上位移的变化, 系统地总结了过渡段路基的纵向和横向动力响应规律。
1. 模型的建立
ANSYS瞬态动力学分析(亦称时间历程分析) 是用于确定承受任意的随时间变化荷载结构的动力学响应的一种方法。ANSYS程序使用Newmark时间积分方法在离散的时间点上求解这些方程。ANSYS进行瞬态动力学分析可采用3种方法: Full Method (完全法)、Reduced Method (缩减法)、Mode Superposition Method。完全法采用完整系统矩阵计算瞬态响应(没有矩阵缩减), 是3种方法中功能最强的, 允许包括各类非线性特性(塑性、大变形、大应变等)。完全法的优点是容易使用, 不必关心选择主自由度或振型, 采用完整矩阵, 不涉及质量矩阵近似, 在一次处理过程中计算出所有的位移和应力, 允许施加所有类型的荷载, 包括节点力与单元荷载等, 因此, 本论文采用完全法进行计算, 分析过程主要由3步组成。
(1) 建模:
主要是用PREP7定义单元类型、单元实常数、材料性质及几何模型等。
(2) 加载:
主要分为进入ANSYS求解器, 指定分析类型和分析选项, 在模型上加载, 保存当前荷载步设置到荷载步文件中与开始求解。
(3) 观察结果:
主要利用后处理命令进行结果观察与计算。
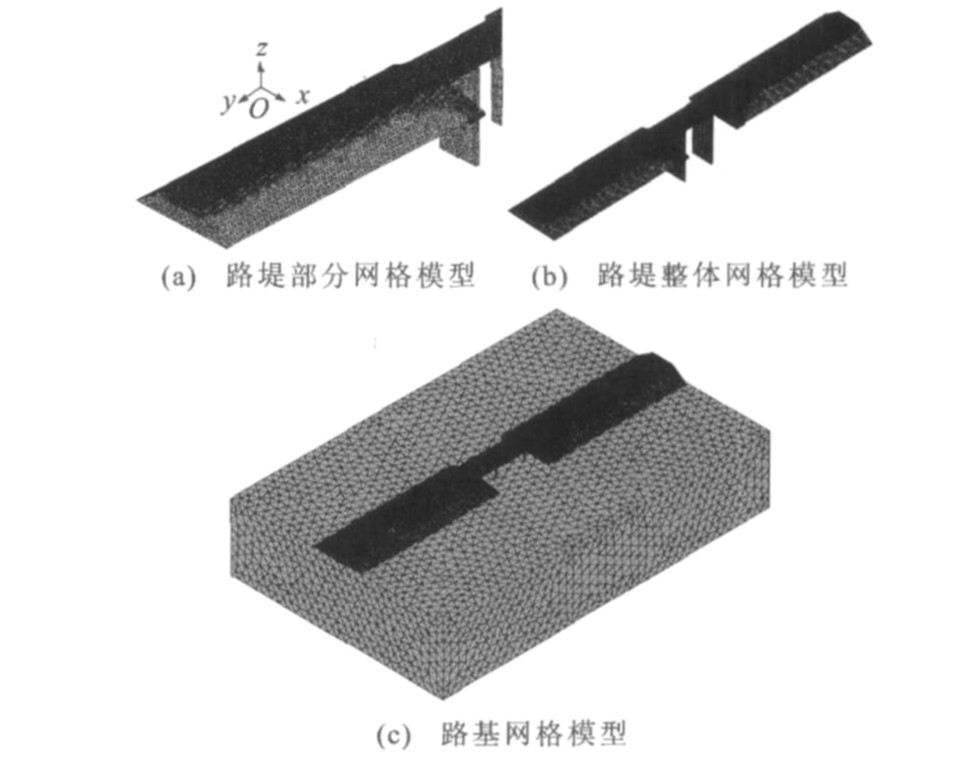
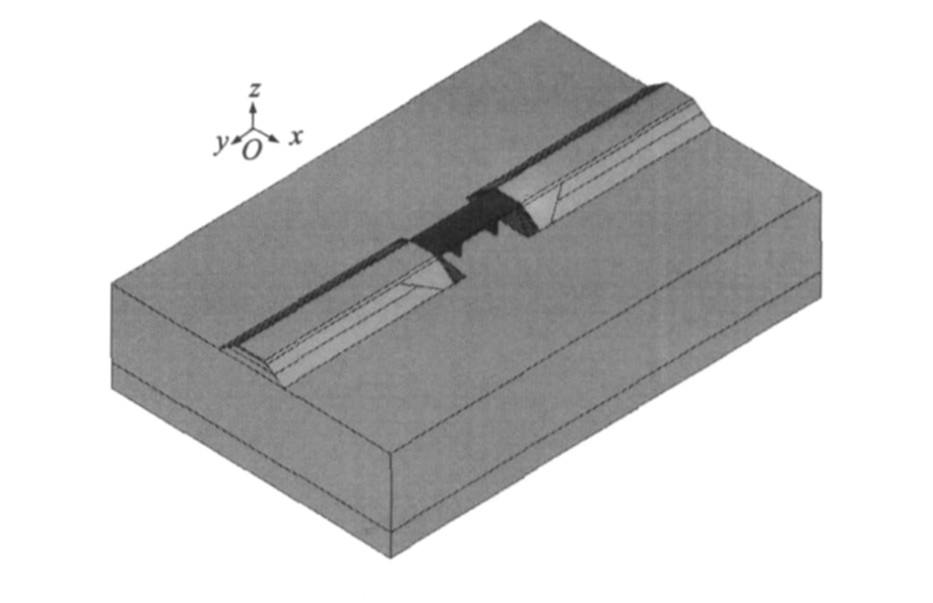
过渡段路基整体模型见图 1。模型尺寸参考现场实际条件, 整体长度取200 m, 桥梁长度为40 m, 宽度为12 m, 两边路基各取80 m。桥台高度为7 m, 桥墩高度为25 m。过渡段长度为20 m, 为倒梯形结构, 坡度为1∶2, 厚度为5.3 m。路堤顶宽为12 m, 底宽为30 m, 坡度为1∶1.5, 高度为6 m, 其中基床表层厚度为0.7 m, 基床底层厚度为2.3 m, 路堤底层厚度为3 m。地基尺寸为(长×宽×高) 200 m×130 m×40 m, 基岩厚度为10 m。
有限元模型采用三维结构实体单元建模, 模型计算参数与二维模型参数相同, 单元类型选用八节点六面体实体单元SOLID45与SOLID65。模型边界条件为路基两侧x、z向全约束, 即只有竖向变形; 地基底部全约束; 桥梁为简支梁形式, 即一端全约束, 另一端只有纵向移动; 桥台与过渡段和基床表层接触部分设置摩擦系数为0.3, 桥台外侧只有纵向移动, 底部全约束; 桥梁支撑底部全约束。路基有限元网格见图 2。桥台与过渡段路基接触的单元类型为TARGE169和CONTA171, 其中摩擦系数取0.3。模型主要计算参数见表 1。
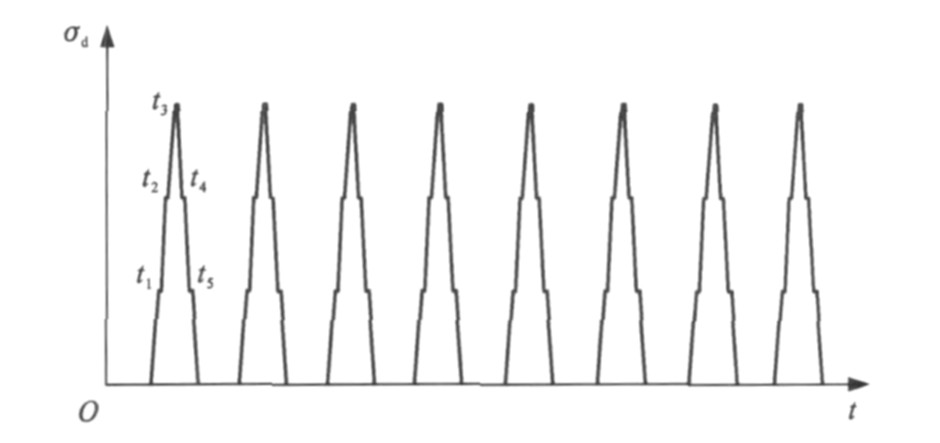
表 1 主要计算参数Table 1. Main computational parameters名称 密度/ (kg·m-3) 弹性模量/MPa 泊松比 过渡段 2 000 120 0.256 基床表层 1 850 100 0.360 基床底层 1 800 80 0.360 路堤底层 1 800 60 0.356 地基 1 800 60 0.356 桥台 2 500 20 000 0.200 桥 2 500 30 000 0.200 桥墩 2 500 20 000 0.200 由文献[3-11]可知, 路基面上的动应力为单向脉冲面力, 本文计算得到的典型动应力-时间曲线见图 3, 可以看出, 路基面上动应力可表示为单向脉冲应力形式。在ANSYS中可以表示为图 4, 为时间的脉冲荷载函数形式。而动应力幅值大小为
σd=βΡ(1+αV)
式中: β为动应力轴载系数; P为列车静轴载; 1+αV为冲击系数, V为速度, α为常数, 一般取0.003。
2. 两车相向移动时过渡段路基动力响应特性分析
为模拟现场的实际情况, 对过渡段在两车相向移动时的动力响应情况进行模拟分析, 由于上行车为载货运行, 下行车为空车运行, 因此, 考虑到荷载对过渡段路基的影响范围, 将上行荷载模拟为5 m×20 m的面力, 下行荷载模拟为4 m×20 m的面力, 荷载大小分别为85 kPa和75 kPa。相向移动时上行车从过渡段向桥移动, 下行车由桥向过渡段移动, 两荷载初始相距20 m。
2.1 动应力纵向变化规律
动应力纵向上随时间变化曲线与实测动应力曲线变化规律相似, 左侧距路基中心2.5 m处的最大动应力为84 kPa, 大于右侧距路基中心3.0 m最大动应力80 kPa。由表 2、3不同位置中动应力均值来看, 在荷载作用中心下的左右两侧路基2.5 m (左侧) 和3.0 m (右侧) 处, 在过渡段20 m范围内动应力均值范围为36~37 kPa; 而过渡段外则逐渐减小; 路基表面中心动应力均值则很小。
表 2 路基表面距路基中心2.5 m处的动应力均值Table 2. Dynamic stress averages of subgrade surface with 2.5 m distance from subgrade center距桥台背距离/m 5.5 8.0 10.0 12.0 15.0 16.0 18.0 20.0 21.0 22.0 23.0 24.0 25.0 动应力均值/kPa 36 36 36 36 36 37 36 37 36 34 32 31 29 表 3 路基表面距路基中心3.0 m处的动应力均值Table 3. Dynamic stress averages of subgrade surface with 2.5 m distance from subgrade center距桥台背距离/m 5.25 8.25 10.25 15.25 18.25 20.25 22.25 23.25 24.25 25.25 动应力均值/kPa 36 36 36 36 36 36 33 31 29 27 荷载下方路基面动应力最大值σmax与最大值沿线路纵向扩散距离L关系可表示为
L=σmax/(8.290+0.617σmax)
式中: σmax以kPa计; L以m计。
2.2 动位移横向变化规律
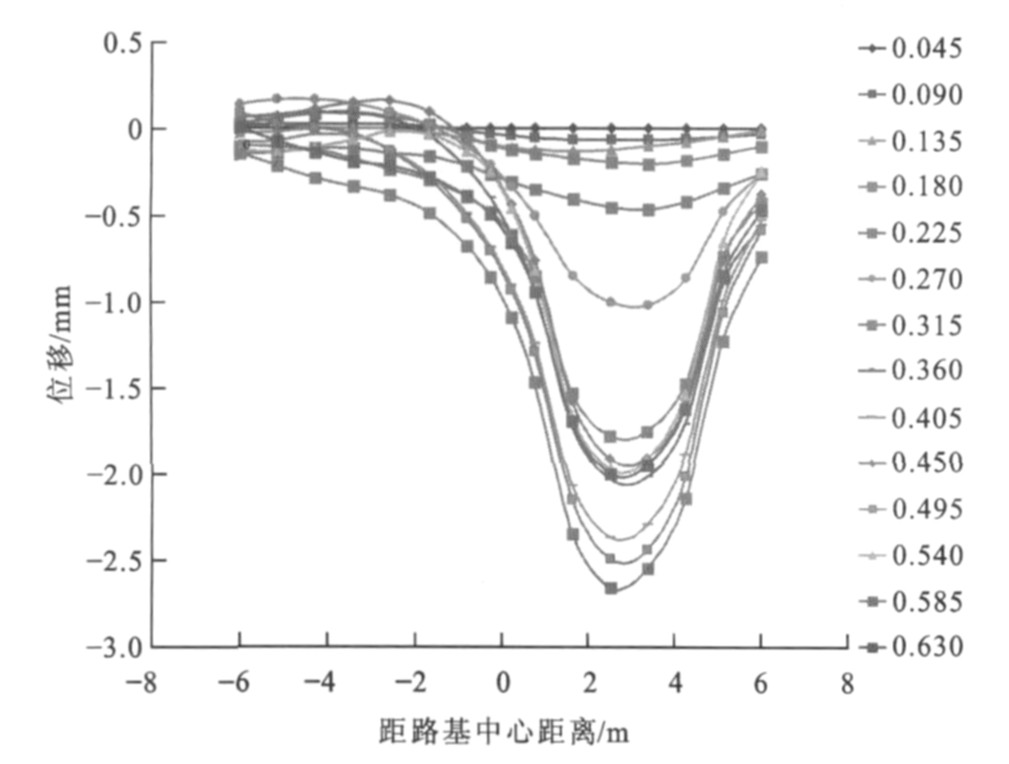
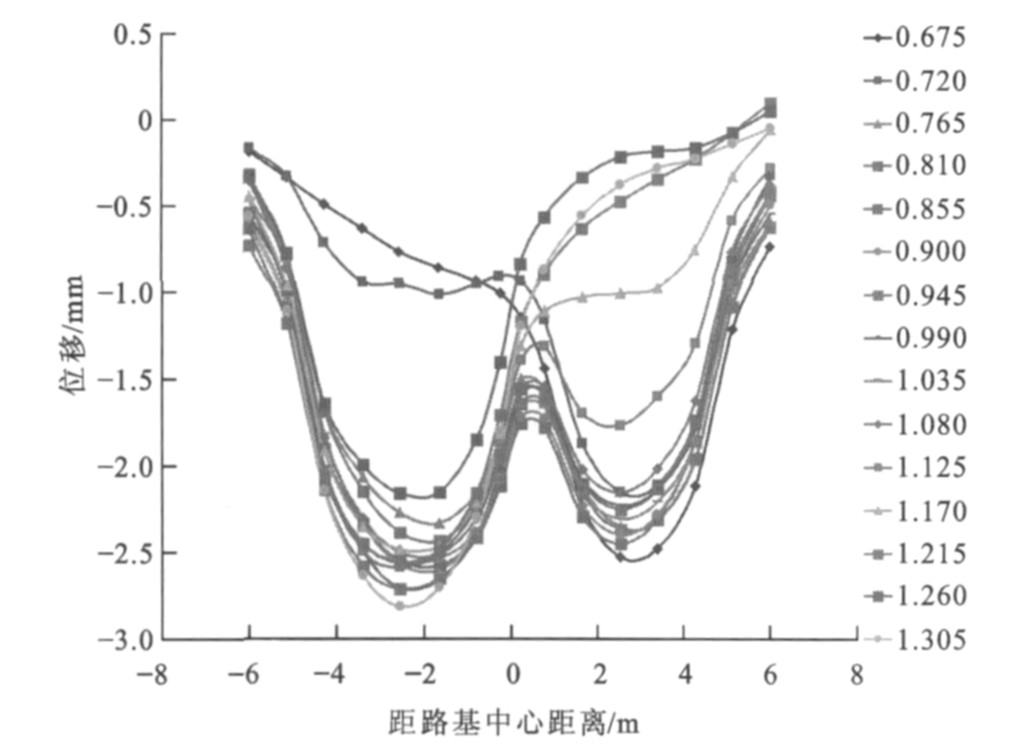
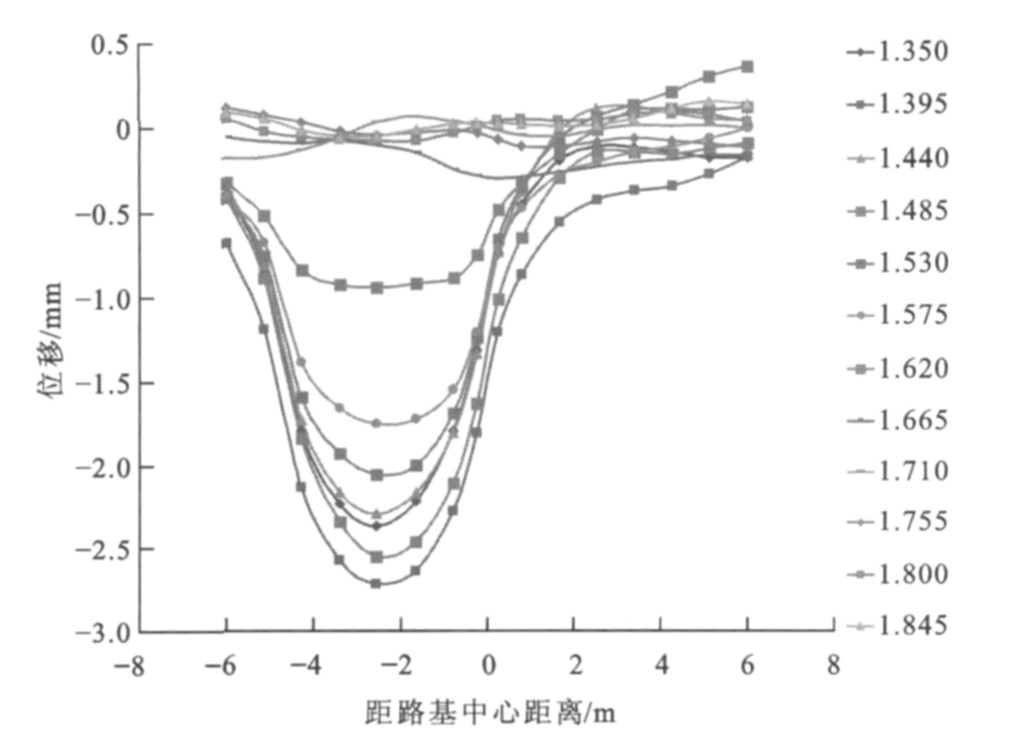
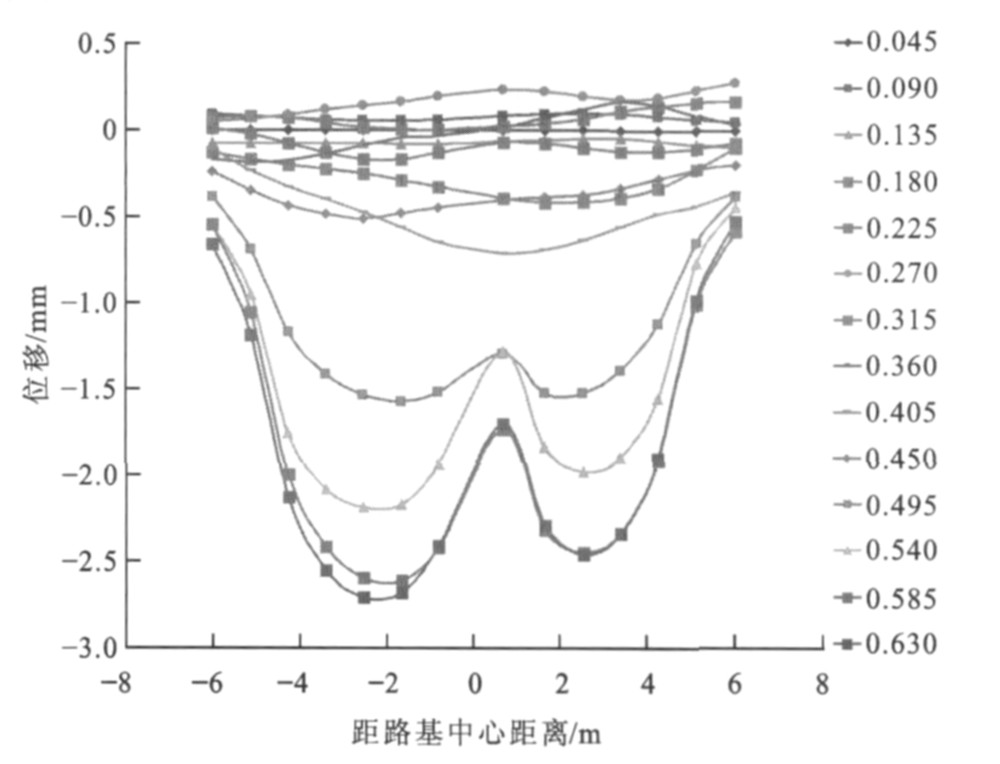
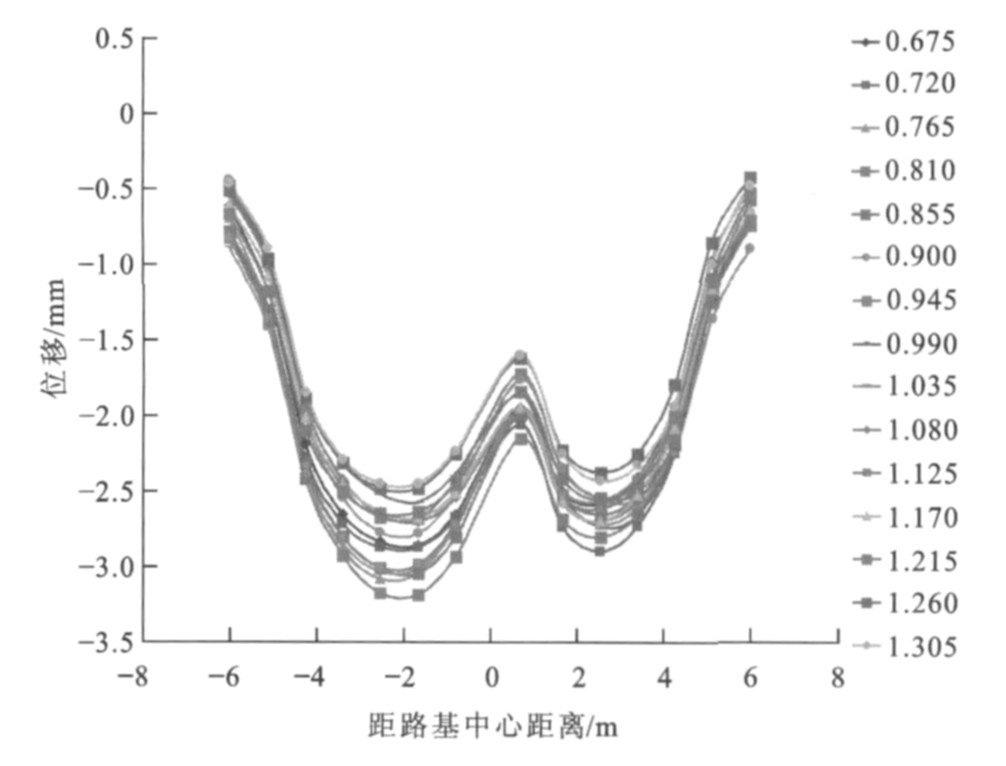
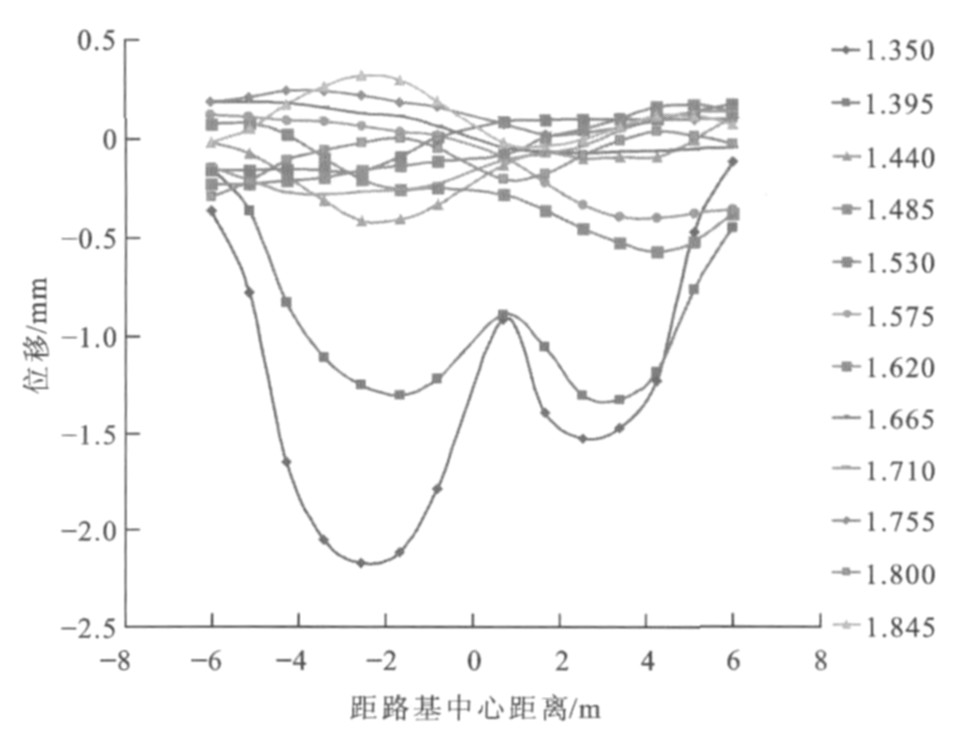
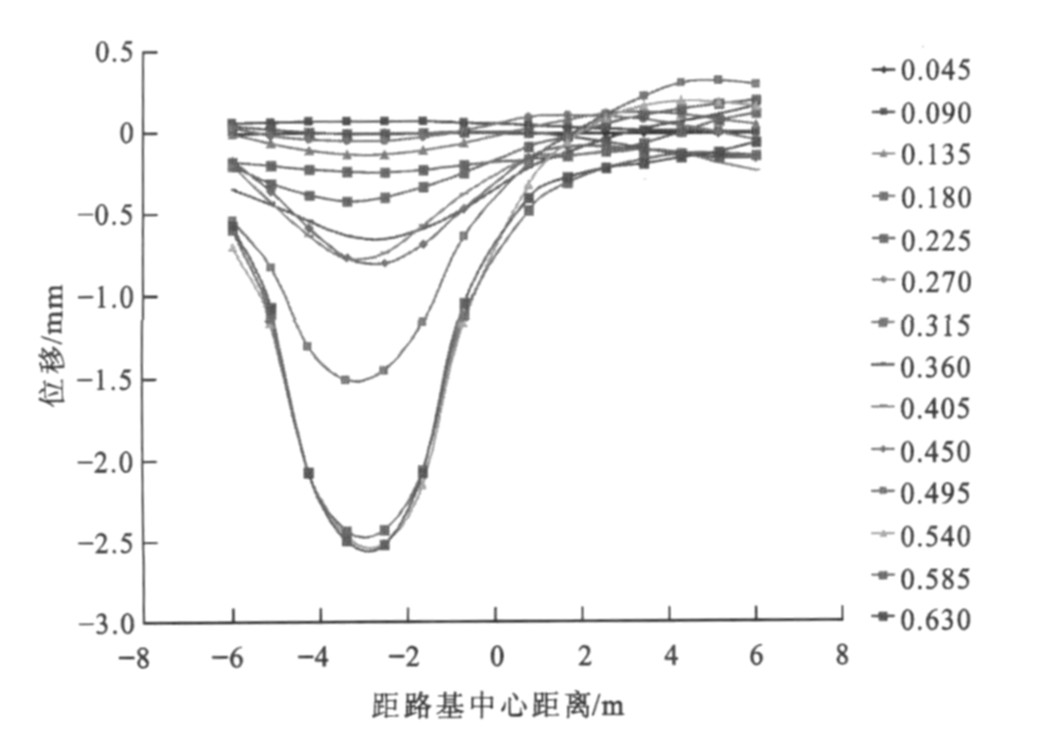
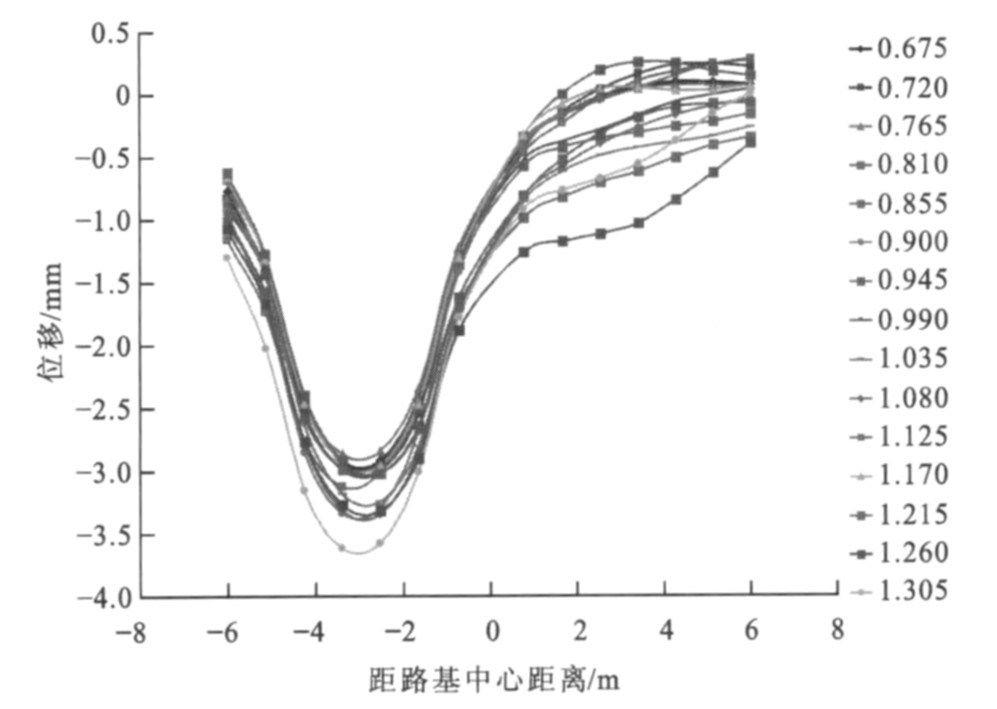
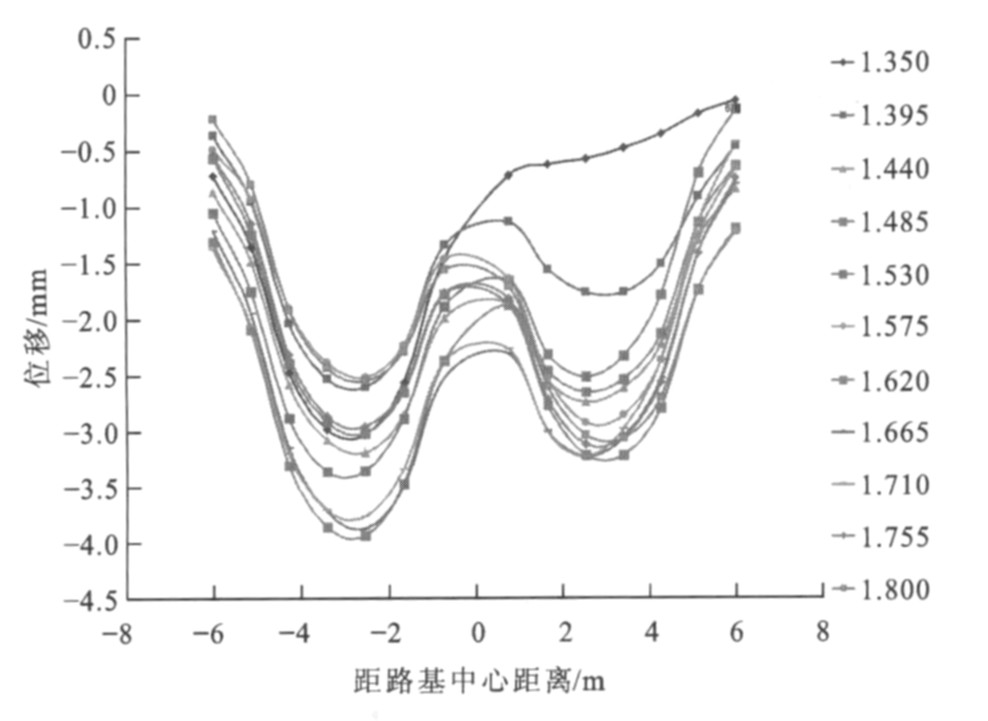
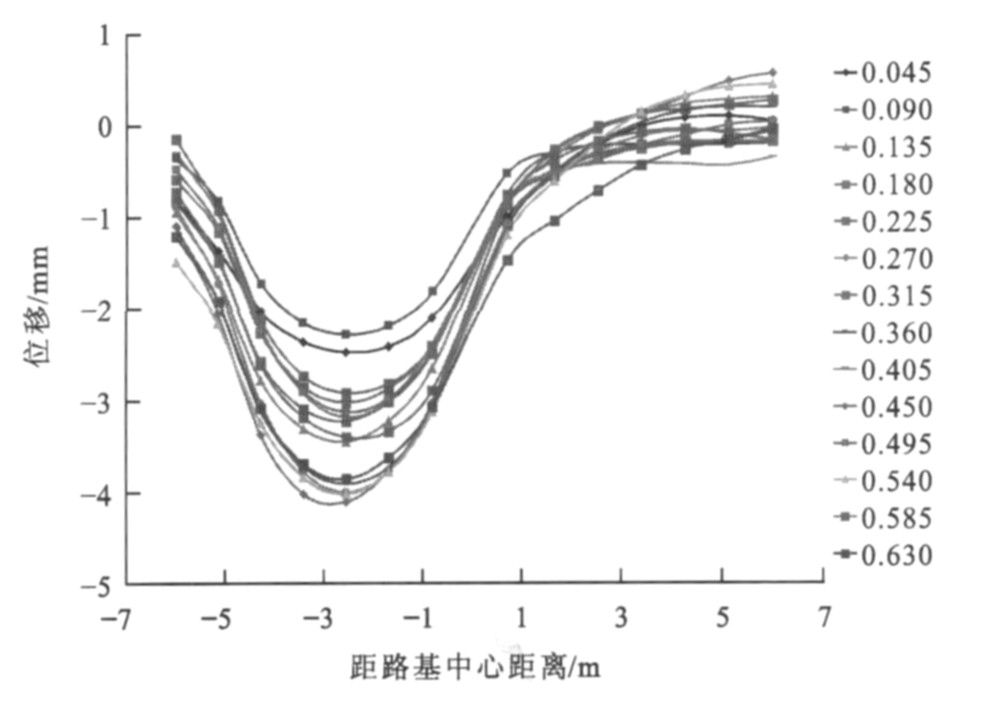
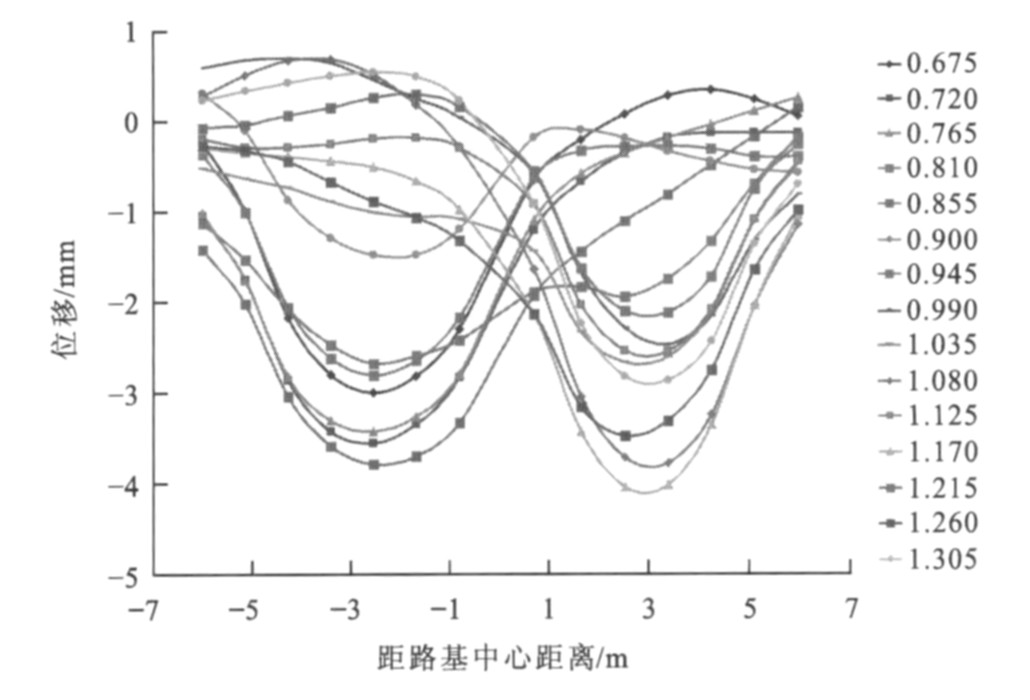
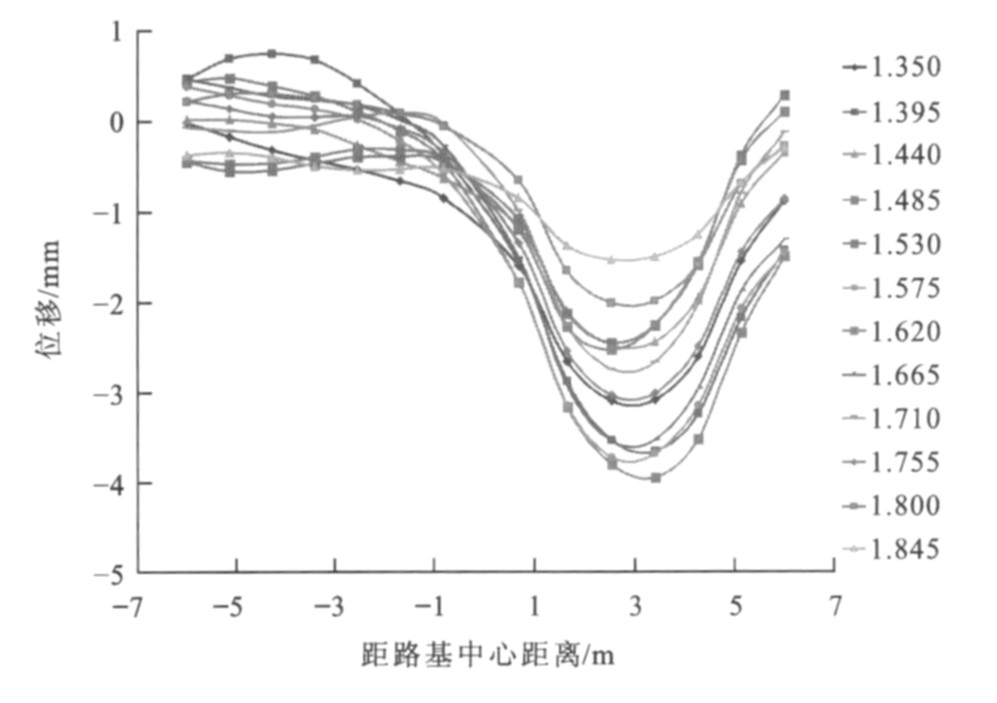
相向移动荷载作用下距桥台背不同距离处路基横向上各点(时间点, 单位为s) 位移变化见图 5~16, 0表示路基中心, 负号表示中心左侧路基, 正号表示中心右侧路基。很明显, 路基左右两侧均有峰值点, 曲线呈“W”形状, 即左右两侧荷载作用面积中心下的位移最大, 左侧为距路基中心2.5 m处, 右侧为距路基中心3.0 m处; 同时位移随作用时间的增加而累积增大, 达到一定时间后位移又从峰值点开始减小, 在路基中心处位移并非最小, 荷载对左右两侧的位移均有影响。
图 5 离桥台背5.0 m路基表面横向各点位移曲线1Figure 5. The first cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 6 离桥台背5.0 m路基表面横向各点位移曲线2Figure 6. The second cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 7 离桥台背5.0 m路基表面横向各点位移曲线3Figure 7. The third cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 8 离桥台背10.0 m路基表面横向各点位移曲线1Figure 8. The first cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 9 离桥台背10.0 m路基表面横向各点位移曲线2Figure 9. The second cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 10 离桥台背10.0 m路基表面横向各点位移曲线3Figure 10. The third cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 11 离桥台背15.0 m路基表面横向各点位移曲线1Figure 11. The first cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 12 离桥台背15.0 m路基表面横向各点位移曲线2Figure 12. The second cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 13 离桥台背15.0 m路基表面横向各点位移曲线3Figure 13. The third cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 14 离桥台背20.0 m路基表面横向各点位移曲线1Figure 14. The first cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment
图 15 离桥台背20.0 m路基表面横向各点位移曲线2Figure 15. The second cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment
图 16 离桥台背20.0 m路基表面横向各点位移曲线3Figure 16. The third cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment离桥台背5.0 m处左侧位移最大峰值为2.81 mm, 右侧位移最大峰值为2.65 mm, 差值为0.16 mm; 左侧曲线最大峰值点发生在1.305 s, 右侧发生在0.585 s, 之后峰值点逐渐减小。同时发现, 0.810~1.035 s的各时间对应的曲线均有左右2个峰值点, 此时曲线还在路基中心偏右处有波谷点, 且左侧峰值大于右侧峰值, 原因是该段时间两荷载相应的移动距离为18~23 m, 此时相交荷载长度为14~20 m, 即在过渡段左右两侧的交会距离, 恰好为两荷载由全部作用在过渡段到开始离开过渡段的长度。离桥台背10.0 m处左侧位移最大峰值为3.18 mm, 右侧位移最大峰值为2.90 mm, 差值为0.28 mm; 左侧曲线最大峰值点发生在0.945 s, 右侧发生在0.720 s, 之后峰值点逐渐减小。0.500~1.305 s的各时间对应的曲线均有左右2个峰值点, 此时曲线还在路基中心偏右处有波谷点, 且左侧峰值大小大于右侧峰值, 原因是该段时间两荷载相应的移动距离为10~26 m, 此时相交荷载长度为0~20 m, 恰好为两荷载由开始相交到开始错开的时候。离桥台背15.0 m处左侧位移最大峰值为3.79 mm, 右侧位移最大峰值为3.45 mm, 差值为0.34 mm。离桥台背20.0 m处左侧位移最大峰值为4.11 mm, 右侧位移最大峰值为4.05 mm, 差值为0.06 mm, 之后峰值点逐渐减小。
3. 结语
(1) 相向移动荷载作用下路基横向上各点的位移曲线呈“W”形状, 路基左右两侧均有峰值点, 即左右两侧荷载作用面积中心下的位移最大, 左侧为距路基中心2.5 m处, 右侧为距路基中心3.0 m处。
(2) 路基中心左侧和右侧由于荷载作用面积的不同, 荷载影响范围存在差异; 路基左侧的最大位移要大于右侧的最大位移, 点离荷载中心越近, 该点位移波动变化越剧烈; 相向移动的荷载对位移的变化影响显著, 说明双线的过渡段影响范围更大。
(3) 路基横向上各点位移随作用时间增加而累积增大, 到一定时间后位移又从峰值点开始减小。在路基中心处位移并非最小, 荷载对左右两侧的位移均有影响。
(4) 荷载除了对其作用一侧的路基位移有影响外, 又加剧了路基另一侧的位移。
(5) 沿路基深度方向上, 荷载对路基位移的影响逐渐减弱。
-
图 5 离桥台背5.0 m路基表面横向各点位移曲线1
Figure 5. The first cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 6 离桥台背5.0 m路基表面横向各点位移曲线2
Figure 6. The second cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 7 离桥台背5.0 m路基表面横向各点位移曲线3
Figure 7. The third cluster of displacement curves of subgrade surface transverse points with 5.0 m distance from abutment
图 8 离桥台背10.0 m路基表面横向各点位移曲线1
Figure 8. The first cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 9 离桥台背10.0 m路基表面横向各点位移曲线2
Figure 9. The second cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 10 离桥台背10.0 m路基表面横向各点位移曲线3
Figure 10. The third cluster of displacement curves of subgrade surface transverse points with 10.0 m distance from abutment
图 11 离桥台背15.0 m路基表面横向各点位移曲线1
Figure 11. The first cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 12 离桥台背15.0 m路基表面横向各点位移曲线2
Figure 12. The second cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 13 离桥台背15.0 m路基表面横向各点位移曲线3
Figure 13. The third cluster of displacement curves of subgrade surface transverse points with 15.0 m distance from abutment
图 14 离桥台背20.0 m路基表面横向各点位移曲线1
Figure 14. The first cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment
图 15 离桥台背20.0 m路基表面横向各点位移曲线2
Figure 15. The second cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment
图 16 离桥台背20.0 m路基表面横向各点位移曲线3
Figure 16. The third cluster of displacement curves of subgrade surface transverse points with 20.0 m distance from abutment
表 1 主要计算参数
Table 1. Main computational parameters
名称 密度/ (kg·m-3) 弹性模量/MPa 泊松比 过渡段 2 000 120 0.256 基床表层 1 850 100 0.360 基床底层 1 800 80 0.360 路堤底层 1 800 60 0.356 地基 1 800 60 0.356 桥台 2 500 20 000 0.200 桥 2 500 30 000 0.200 桥墩 2 500 20 000 0.200 
下载: 导出CSV
表 2 路基表面距路基中心2.5 m处的动应力均值
Table 2. Dynamic stress averages of subgrade surface with 2.5 m distance from subgrade center
距桥台背距离/m 5.5 8.0 10.0 12.0 15.0 16.0 18.0 20.0 21.0 22.0 23.0 24.0 25.0 动应力均值/kPa 36 36 36 36 36 37 36 37 36 34 32 31 29
下载: 导出CSV
表 3 路基表面距路基中心3.0 m处的动应力均值
Table 3. Dynamic stress averages of subgrade surface with 2.5 m distance from subgrade center
距桥台背距离/m 5.25 8.25 10.25 15.25 18.25 20.25 22.25 23.25 24.25 25.25 动应力均值/kPa 36 36 36 36 36 36 33 31 29 27
下载: 导出CSV
-
[1] SHAMSABADI A. Three-dimensional nonlinear seismic soil abut ment-foundation-structure interaction analysis of skewed bridges[D]. Los Angeles: University of Southern California, 2007. [2] 罗强. 高速铁路路桥过渡段动力学特性分析及工程试验研究[D]. 成都: 西南交通大学, 2003.LUO Qiang. Dynamic performance analyses and experiment studyon bridge/approach embankment of high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2003. (in Chinese) [3] 陶向华. 路桥过渡段差异沉降控制标准与人车路相互作用[D]. 南京: 东南大学, 2006.TAO Xiang-hua. Differential settlement control criterion of bridge-approach and people-vehicle-road interaction[D]. Nanjing: Southeast University, 2006. (in Chinese) [4] 张洪亮. 路桥过渡段车路动力学分析及容许差异沉降研究[D]. 西安: 长安大学, 2003.ZHANG Hong-liang. Study on the dynamic vehicle-roadway interaction and tolerable differential settlement on the bridge approach[D]. Xi an: Chang an University, 2003. (in Chinese) [5] 李献民. 高速铁路加筋过渡段静动力特性数值分析及试验研究[D]. 长沙: 中南大学, 2004.LI Xian-min. Numerical analysis andtest study onthe statical and dynamical characteristics of high-speed rail way transition section reinforced by geogrid[D]. Changsha: Central South University, 2004. (in Chinese) [6] 陈震. 高速铁路路基动力响应研究[D]. 武汉: 中国科学院武汉岩土力学研究所, 2006.CHEN Zhen. Research on dynamic response of high speed rail way[D]. Wuhan: Wuhan Institute of Rock and Soil Mechanics, the Chinese Academy of Sciences, 2006. (in Chinese) [7] OKADA K, GHAT AORA G S.Use of cyclic penetration test to estimate the stiffness of railway subgrade[J].NDT and E International, 2002, 35(2):65-74.(in Chinese) [8] 罗强, 蔡英, 翟婉明. 高速铁路路桥过渡段的动力学性能分析[J]. 工程力学, 1999, 16 (5): 65-70. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX199905009.htmLUO Qiang, CAI Ying, ZHAI Wan-ming. Dynamic perform-ance analyses on high speed rail way bridge-subgrade transi-tion[J]. Engineering Mechanics, 1999, 16 (5): 65-70. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX199905009.htm [9] 聂志红, 阮波, 李亮. 铁路道床路基动力响应的参数影响[J]. 交通运输工程学报, 2004, 4 (1): 34-37. http://transport.chd.edu.cn/article/id/200401009NIE Zhi-hong, RUAN Bo, LI Liang. Dynamic response parameters of railway ballast-subgrade[J]. Journal of Traffic and Transportation Engineering, 2004, 4 (1): 34-37. (in Chinese) http://transport.chd.edu.cn/article/id/200401009 [10] 梁波, 罗红, 孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报, 2006, 28 (4): 89-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200604018.htmLI ANG Bo, LUO Hong, SUN Chang-xin. Simulated study on vibration load of high speed rail way[J]. Journal of the China Rail way Society, 2006, 28 (4): 89-94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200604018.htm [11] 马伟斌. 既有线提速基床与道床相互影响的研究[D]. 北京: 中国铁道科学研究院, 2006.MA Wei-bin. Research of interaction between the subgrade bed and the ballast bed on existing speed-raising railways[D]. Beijing: China Academy of Rail way Sciences, 2006. (in Chinese) -
下载:
点击查看大图
计量
- 文章访问数: 775
- HTML全文浏览量: 160
- PDF下载量: 302
- 被引次数: 0
