Reynolds number effect of streamlined bridge section
Article Text (Baidu Translation)
-
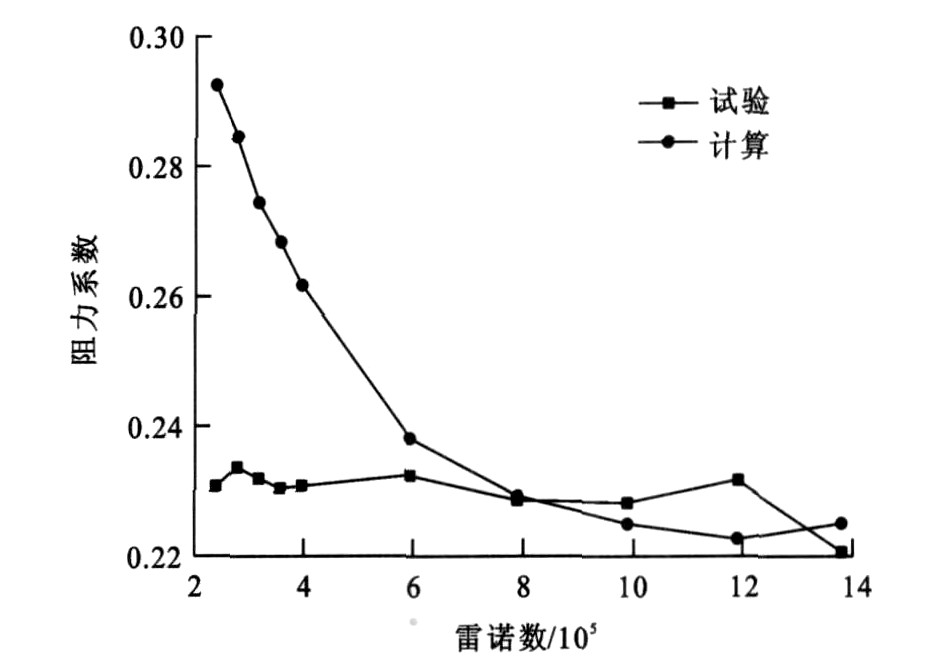
摘要: 采用数值模拟方法计算了不同雷诺数苏通桥流线型断面三分力系数, 通过风洞试验研究了宽高比为10∶1的流线型桥梁断面的雷诺数效应, 分析了雷诺数对阻力系数、表面压力系数、风压功率谱及斯特罗哈数的影响, 研究了粗糙度对雷诺数效应的抑制作用。分析结果表明: 阻力系数随雷诺数的增大而减小, 雷诺数会改变表面压力系数0值出现的位置, 斯特罗哈数对雷诺数有平台区存在, 低雷诺数风洞试验测得的斯特罗哈数比实桥值小20%, 因此, 流线型桥梁断面存在明显的雷诺数效应, 且粗糙度对雷诺数效应有抑制作用。Abstract: The three-component force coefficients of streamlined sections of Sutong Bridge with different Reynolds numbers were calculated by using numerical simulation. The Reynolds number effect of streamlined section for bridge model with chord/thickness ratio of 10∶1 was investigated by wind tunnel test, the influence of Reynolds number on drag coefficient, surface pressure coefficient, wind pressure spectrum and Strouhal number was analyzed, and the restraining action of surface roughness on Reynolds number effect was researched. It is pointed that drag coefficient decreases with the increase of Reynold number. The zero position of surface pressure coefficient is subject to the influence of Reynolds number. Strouhal number exists platform effect because of the influence of Reynolds number. Strouhal number measured by wind tunnel test with low Reynolds number decreases by 20% compared with the one of practical bridge. Reynolds number effect of streamlined section is considerable. Surface roughness can restrain Reynolds number effect.
-
图 4 上下表面最小压力系数变化
Figure 4. Changes of minimum pressure coefficients on upper surface and under surface
图 8 考虑粗糙度的上下表面最小压力系数变化
Figure 8. Changes of minimum pressure coefficients on upper surface and under surface under considering roughnesses
-
[1] LAROSE G L, AUTEUIL A D. On the Reynolds number sensitivity of the aerodynamics of bluff bodies with sharp edges[J]. Journal of Wind Engineering and Industrial Aero-dynamics, 2006, 94(2): 365-376. [2] LARSEN A, SAVAGE A, LAFRENIERE A, et al. Investi-gation of vortex response of a twin box bridge section at high and low Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 934-944. [3] 李加武, 林志兴, 项海帆. 桥梁断面三分力系数的雷诺数效应[J]. 同济大学学报: 自然科学版, 2004, 32(10): 1328-1333. doi: 10.3321/j.issn:0253-374X.2004.10.013LI Jia-wu, LI NZhi-xing, XI ANG Hai-fan. Reynolds number effect of mean force coefficient of two kinds of typical bridge deck section[J]. Journal of Tongji University: Natural Science, 2004, 32(10): 1328-1333. (in Chinese) doi: 10.3321/j.issn:0253-374X.2004.10.013 [4] 李加武, 张宏杰, 韩万水. 斜拉桥风致响应的雷诺数效应[J]. 中国公路学报, 2009, 22(2): 42-47. doi: 10.3321/j.issn:1001-7372.2009.02.008LI Jia-wu, ZHANG Hong-jie, HAN Wan-shui. Wind-induced response of cable-stayed bridge with consideration of Reyn-olds number effect[J]. China Journal of Highway and Trans-port, 2009, 22(2): 42-47. (in Chinese) doi: 10.3321/j.issn:1001-7372.2009.02.008 [5] HUANG Wen-rui, YANG Qi-ping, XI AO Hong. CFD mod-eling of scale effects on turbulence flow and scour around bridge piers[J]. Computers and Fluids, 2009, 38(5): 1050-1058. doi: 10.1016/j.compfluid.2008.01.029 [6] CHAKRABRATI S K, DEBUS K K, BERKOE J, et al. CFD analysis of current-induced loads on large caisson at supercritical Reynolds number[J]. Journal of Offshore Mechanics and Arctic Engineering, 2005, 127(2): 104-111. doi: 10.1115/1.1894409 [7] 白桦, 李加武, 胡兆同, 等. 近流线型断面静力三分力系数的雷诺数效应识别[J]. 建筑科学与工程学报, 2007, 24(4): 60-63. doi: 10.3321/j.issn:1673-2049.2007.04.011BAI Hua, LI Jia-wu, HU Zhao-tong, et al. Identification of Reynolds number effect of tri-component force coefficient of streamline-liked section[J]. Journal of Architecture and Civil Engineering, 2007, 24(4): 60-63. (in Chinese) doi: 10.3321/j.issn:1673-2049.2007.04.011 [8] 李加武, 林志兴, 项海帆. 扁平箱形桥梁断面静气动力系数雷诺数效应研究[J]. 公路, 2004(9): 43-47. doi: 10.3969/j.issn.0451-0712.2004.09.009LI Jia-wu, LI NZhi-xing, XI ANG Hai-fan. Astudy on Reyn-olds number effect of mean aerodynamic force coefficient of box-beambridge deck sections[J]. Highway, 2004(9): 43-47. (in Chinese) doi: 10.3969/j.issn.0451-0712.2004.09.009 [9] 崔欣. 流线型桥梁断面雷诺数效应及其控制措施研究[D]. 西安: 长安大学, 2008.CUI Xin. Investigationinto Reynolds-number effects of stre-amline-like bridge deck section and mitigating measure[D]. Xi an: Chang an University, 2008. (in Chinese) [10] 李加武, 林志兴, 项海帆. 极端桥梁断面雷诺数效应研究[J]. 郑州大学学报: 工学版, 2003, 24(2): 22-25. doi: 10.3969/j.issn.1671-6833.2003.02.006LI Jia-wu, LI N Zhi-xing, XI ANG Hai-fan. Study on the Reynolds number effect of two extreme bridge sections[J]. Journal of Zhengzhou University: Engineering Science, 2003, 24(2): 22-25. (in Chinese) doi: 10.3969/j.issn.1671-6833.2003.02.006 [11] 李加武. 桥梁断面雷诺数效应及其控制研究[D]. 上海: 同济大学, 2003.LI Jia-wu. Research on Reynolds-number effects of bridge deck section and the effects-restraint[D]. Shanghai: Tongji University, 2003. (in Chinese) [12] 许福友, 陈艾荣, 黄才良, 等. 大跨桥梁风洞试验模型模态耦合分析[J]. 中国公路学报, 2009, 22(3): 58-63. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200903010.htmXU Fu-you, CHEN Ai-rong, HUANG Cai-liang, et al. Modal coupling analysis of long-span bridge model in wind tunnel test[J]. China Journal of Highway and Transport, 2009, 22(3): 58-63. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200903010.htm [13] 周立, 葛耀君. 上海长江大桥节段模型气动三分力试验[J]. 中国公路学报, 2007, 20(5): 48-53. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200705010.htmZHOU Li, GE Yao-jun. Experiment on three-component of aerodynamic force of sectional model for Shanghai Yangtze River Bridge[J]. China Journal of Highway and Transport, 2007, 20(5): 48-53. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200705010.htm [14] 胡庆安, 乔云强, 刘健新, 等. 斜风作用下桥塔施工阶段抖振性能[J]. 交通运输工程学报, 2008, 8(2): 40-43. http://transport.chd.edu.cn/article/id/200802009HU Qing-an, QIAO Yun-qiang, LIUJian-xin, et al. Buffeting performance of bridge tower under yawed wind during construction[J]. Journal of Traffic and Transportation Engineering, 2008, 8(2): 40-43. (in Chinese) http://transport.chd.edu.cn/article/id/200802009 [15] 李加武, 崔欣, 张宏杰, 等. 粗糙度对雷诺数效应的影响[J]. 长安大学学报: 自然科学版, 2009, 29(2): 56-59, 64. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200902016.htmLI Jia-wu, CUI Xin, ZHANG Hong-jie, et al. Influence of surface roughness on Reynolds number effects[J]. Journal of Chang an University: Natural Science Edition, 2009, 29(2): 56-59, 64. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL200902016.htm -
下载:
点击查看大图
图(9)
计量
- 文章访问数: 1051
- HTML全文浏览量: 261
- PDF下载量: 597
- 被引次数: 0
