0.   引言

随着中国城市公路运输的快速发展, 公共停车场供给不足同日益增长的车辆之间的矛盾十分突出, 因此, 公共停车场的管理已成为当前中国城市交通管理中一个十分重要的问题。对于公共停车场的收费和规模管理问题, 已有一些相应的研究。周智勇等运用层次分析法对城市停车设施规划进行决策^[1]; 姜涛等对城市机动车的收费定价问题及其对居民出行方式的选择作了相应的研究^[2-5]; 梅振宇等对停车场规模优化和规划进行了研究^[6-10]; Arnott等运用理论模型对公共停车场的停车费和拥挤管理进行研究^[11-12]; Tsai等对公有停车管理公司和私人停车管理公司共存情况下的停车费问题进行研究^[13]; Button运用新古典经济学方法和博弈模型对停车场的“最优”和“次优”收费模式进行经济分析^[14]; 而Hensher等则就停车收费管理问题进行了实证研究^[15-17]。

从已有的研究中可见, 由于公共停车场具有一定的公益性质, 属于经济学中的“准公共品”, 因此, 政府在公共停车场的管理中具有主导地位。由于管理效率的低下, 因此, 将公共停车场的管理交给私人停车管理公司进行管理似乎是必然趋势。但如果对私人停车管理公司不加控制的话, 其单纯追求利润最大化的行为又会危害社会福利, 如何采取有效的措施对经营停车场的私人停车管理公司进行控制成为当前公共停车场管理的热点问题。具体而言, 对公共停车场的管理可以采用两种形式。一种为公共停车场通过招标的方式完全由某个私人停车管理公司进行经营, 政府设计具体的规则对其进行直接监控, 下文简称为规制经营模式。在该种模式下, 由于政府不直接参与停车场的经营管理, 对私人停车管理公司的成本信息不了解, 因此, 政府必须通过适当的机制设计来诱导私人停车管理公司的经营行为, 政府根据其业绩指标对其进行奖励或惩罚。另一种则将公共停车场分为两部分, 一部分交给政府下属的公有停车管理公司经营, 另一部分通过租赁的方式由私人停车管理公司经营, 下文简称为竞争经营模式。在该种模式下, 政府通过公有停车管理公司与私人停车管理公司之间的竞争来达到调控私人停车管理公司经营行为的目的。由于此时公有停车管理公司也参与停车场的经营管理, 因此, 政府对停车管理的成本信息有相当了解, 但只能通过与私人停车管理公司竞争的间接方式来对其进行控制, 避免其经营行为给社会福利带来的危害。

现有的研究文献大多假定政府对停车场的经营信息完全掌握, 这在一定程度上与实际情况不完全相符, 而信息不对称对公共停车场的管理制度设计带来了很大的困难。此外, 现有研究对于上述两种公共停车场的管理形式缺乏比较, 这些都会妨碍对公共停车场管理模式的合理选择, 因此, 本文将运用机制设计理论和动态博弈模型, 充分考虑信息不对称的情况, 对上述两种管理模式下公共停车场的最优停车费和规模进行研究, 以期能为相关部门提供决策支持。

1.   停车管理模型的建立

停车服务需求量采用线性函数形式表示为

$D=D{}_0-ap(1)$

式中: D为停车服务需求量; D₀为需求函数中表示市场规模的参数, D₀越大, 表示市场规模越大; a为反映停车服务需求量对价格的敏感程度的参数, a越大表示停车服务需求量对价格的敏感程度越高; p为广义价格, 由两部分构成, 一是停车费用f, 另一部分为用户等待的时间成本, 表示为tD/s, 其中t为等待时间成本的参数, s为停车场的规模。可见, p表示为

$p=f+tD/s(2)$

停车场的成本由两部分构成, 一部分为营运成本, 与停车服务需求量有关, 另一部分为停车场的维护成本, 与停车场的规模有关。维护成本采用二次函数的形式, 因此, 停车场经营的总成本为

$c=\theta D+\tau s{}^2(3)$

式中: θ为停车服务的边际成本; τ为停车场的维护成本参数。f、s、D均为θ、τ的函数。

2.   规制经营模式

2.1   基本假设

假设1:政府缺乏停车场经营管理的成本信息, 即政府不知道θ和τ的具体数值, 只知道θ和τ均为随机变量, $\theta \in [\underset{¯}{\theta },\overline{\theta }]$, 其分布函数为G(θ), 概率密度为g(θ); $\tau \in [\underset{¯}{\tau },\overline{\tau }]$, 其分布函数为M(τ), 概率密度为m(τ)。θ和τ的分布函数和概率密度满足单调似然率条件, 即$\frac{\text{d}}{\text{d}\theta }\left[\frac{G(\theta )}{g(\theta )}\right]\ge 0‚\frac{\text{d}}{\text{d}\tau }\left[\frac{{\rm M}(\tau )}{m(\tau )}\right]\ge 0$, 且θ和τ相互独立, 而私人停车管理公司则确切地知道自己的成本信息θ和τ。$\underset{¯}{\theta }$、$\overline{\theta }$和$\underset{¯}{\tau }$、$\overline{\tau }$分别为θ和τ可取数值的上限和下限。

假设1与规制经营模式下政府同私人停车管理公司之间的信息结构相一致, 表明政府对停车场经营者的成本函数不完全了解, 因此, 在政府的制度设计中存在逆向选择。对于政府而言, 必须通过适当的机制设计来诱导停车场经营者如实地汇报其成本信息, 以便政府能有效地对其控制, 使其行为符合自己的目标。而由于信息不对称现象的存在, 政府的控制活动是有代价的, 这表现在停车费会存在一定程度的扭曲。单调似然率条件则是机制设计文献所普遍采用的标准假设^[16], 大多数常见的分布, 如均匀分布、正态分布、对数分布、卡方分布、指数分布、Laplace分布都满足上述条件。

假设2:政府的目标为最大化社会总福利, 即消费者剩余和私人停车管理公司利润的加权平均值。

假设2是福利经济学中关于政府目标的标准假设^[12], 本文采用了福利经济学中常见的拟线性效用函数和社会福利的功利形式来定义政府的目标, 即政府是“善意的规制者”, 其目标为消费者剩余和私人停车管理公司的利润之和最大化。

假设3:私人停车管理公司向政府上交营运收入, 再由政府根据经营业绩给予私人停车管理公司一定的转移支付, 政府通过转移支付达到对私人停车管理公司奖惩的目的。

由引言中关于规制经营模式的特点可知, 假设3也是公共经济学中常用的假设。

假设4:私人停车管理公司的目标为最大化利润, 即所得的转移支付减去经营成本, 其得到的利润必须大于等于其保留利润, 本文将其保留利润水平标准化为0。

假设4使得政府必须尊重私人停车管理公司的“个人理性”约束或者“参与”约束。如政府不能保证私人停车管理公司获得其最低预期利润水平, 则私人停车管理公司会放弃对停车场的经营管理。

假设5:政府设计制度, 即政府掌握了全部的讨价还价能力, 政府向私人停车管理公司提供的合约为一个“要么接受, 要么离开”式的合约。假设5也是机制设计文献所普遍采用的标准假设^[12]。

2.2   博弈顺序

由于对停车场经营管理的成本参数θ和τ均缺乏信息, 因此, 政府和私人停车管理公司之间进行如下的博弈, 其中θ和τ是私人停车管理公司向政府汇报的成本参数。

(1) 私人停车管理公司向政府汇报其成本参数信息θ、τ, 当然他可能如实汇报θ=θ, τ=τ, 他也有可能作出虚假的汇报θ≠θ, τ≠τ。

(2) 政府根据私人停车管理公司汇报的成本参数θ、τ, 确定停车费f(θ, τ)和停车场的规模s(θ, τ)。

(3) 私人停车管理公司根据政府制定的停车费f(θ, τ)和停车场规模s(θ, τ)开展经营活动, 并上交营运收入。

(4) 政府根据私人停车管理公司汇报的成本参数θ、τ, 给予停车场经营者转移支付T(θ, τ)。

2.3   优化问题

在上述博弈过程下, 政府实际上面临如下的优化问题。

优化问题1为

上述优化问题的目标函数中, W_CG为规制经营模式下社会总福利, E(θ)、E(τ)分别为θ、τ的数学期望, 为消费者剩余减去转移支付和用户等待的时间成本, 即消费者的净福利, V_CG为私人停车管理公司的利润, α为私人停车管理公司的利润在政府目标中的相对权重, α∈[0, 1]。在约束条件中, 式(4)为激励相容条件, 即私人停车管理公司选择使自己利润最大的成本信息 汇报; 式(5)为个人理性条件, 即私人停车管理公司的利润必须大于等于保留利润0。

优化问题1实际上是一个二维的逆向选择问题, 对于该问题, Armstrong等提供了离散情形下的二维逆向选择问题的完整分析^[18]。而Mcafee等对一些具有特殊形式的连续情形下的二维逆向选择问题作了一些分析^[19-20]。本文采用Rochet等提出的最优控制技术^[21-22]来解决上述问题。

首先, 根据显示原理, 任何规制机制都等价于诱使私人停车管理公司显示其真实成本参数的直接显示机制, 即私人停车管理公司接受政府的规制过程, 并如实地汇报自己的成本信息, 因此, 本文将分析限制在直接显示机制上。对于激励相容条件, 由包络定理得

$\begin{array}{l}\frac{\partial V{}_{\text{C}\text{G}}}{\partial \theta }=-D(\theta ,\tau )\\ \frac{\partial V{}_{\text{C}\text{G}}}{\partial \tau }=-s{}^2(\theta ,\tau )\end{array}$

同时由激励相容条件可得T(θ, τ)=V_CG+θD(θ, τ)+τs²(θ, τ)

将上述3式带入优化问题1, 可将优化问题1转换为如下的最优控制问题

$\begin{array}{l}\underset{f,s}{{\displaystyle \max }}{\displaystyle {\int }_{\underset{¯}{\tau }}^{\overline{\tau }}{\displaystyle {\int }_{\underset{¯}{\theta }}^{\overline{\theta }}[}}{\displaystyle {\int }_0^{D}p}\text{d}x-(1-\alpha )V{}_{\text{C}\text{G}}-\theta D-\\ \tau s{}^2-tD{}^2/s]g(\theta )m(\tau )\text{d}\theta \text{d}\tau \\ \text{s}.\text{t}.\frac{\partial V{}_{\text{C}\text{G}}}{\partial \theta }=-D(\theta ,\tau )\\ \frac{\partial V{}_{\text{C}\text{G}}}{\partial \tau }=-s{}^2(\theta ,\tau )\\ V{}_{\text{C}\text{G}}\ge 0\end{array}$

在上述最优控制问题中, f、s为控制变量, V_CG为状态变量。为求解上述最优控制问题, 本文参考文献[21, 22]中方法, 建立Hamilton函数为

$\begin{array}{l}{\rm H}=\left[{\displaystyle {\int }_0^{D}p}\text{d}x-(1-\alpha )V{}_{\text{C}\text{G}}-\theta D-\tau s{}^2-tD{}^2/s\right]\cdot \\ g(\theta )m(\tau )-\lambda {}_{1}D-\lambda {}_{2}s{}^2\end{array}$

式中: λ₁、λ₂分别为θ和τ的协变量。

Hamilton函数的一阶条件为

$\begin{array}{l}\frac{\partial {\rm H}}{\partial f}=\left(\frac{\partial {\displaystyle {\int }_0^{D}p}\text{d}x}{\partial f}-\theta \frac{\partial D}{\partial f}-\frac{2tD}{s}\frac{\partial D}{\partial f}\right)\cdot \\ g(\theta )m(\tau )-\lambda {}_1\frac{\partial D}{\partial f}=0(6)\\ \frac{\partial {\rm H}}{\partial s}=\left[\frac{\partial {\displaystyle {\int }_0^{D}p}\text{d}x}{\partial s}-\theta \frac{\partial D}{\partial s}-2\tau s-t\left(\frac{2D\partial D/\partial s}{s}-\frac{D{}^2}{s{}^2}\right)\right]\cdot \\ g(\theta )m(\tau )-\lambda {}_1\frac{\partial D}{\partial s}-2\lambda {}_{2}s=0(7)\end{array}$

$\frac{\partial {\rm H}}{\partial V{}_{\text{C}\text{G}}}=-(1-\alpha )g(\theta )m(\tau )=-\frac{\text{d}\lambda {}_1}{\text{d}\theta }-\frac{\text{d}\lambda {}_2}{\text{d}\tau }(8)$

由式(1)、(2)可得

$\begin{array}{l}p=\frac{sf+tD{}_0}{s+at}(9)\\ D=\frac{sD{}_0-asf}{s+at}(10)\\ \text{而}\frac{\partial {\displaystyle {\int }_0^{D}p}\text{d}x}{\partial f}=p\frac{\partial D}{\partial f}(11)\\ \frac{\partial {\displaystyle {\int }_0^{D}p}\text{d}x}{\partial s}=p\frac{\partial D}{\partial s}(12)\end{array}$

由式(9)可得

$\frac{\partial D}{\partial f}=\frac{-as}{s+at}(13)$

由式(10)可得

$\frac{\partial D}{\partial s}=\frac{at(D{}_0-af)}{(s+at){}^2}(14)$

将式(11)、(13)代入式(6)可得

$(p-\theta -2tD/s)g(\theta )m(\tau )=\lambda {}_1(15)$

将式(12)、(14)、(15)代入式(7)可得

$(tD{}^2/2s{}^3-\tau )g(\theta )m(\tau )=\lambda {}_2(16)$

由式(8)可得

$\begin{array}{l}\lambda {}_1=(1-\alpha )G(\theta )m(\tau )/2(17)\\ \lambda {}_2=(1-\alpha )g(\theta ){\rm M}(\tau )/2(18)\end{array}$

将式(9)、(10)、(17)、(18)带入式(15)、(16)可得化简的一阶条件为

$\begin{array}{l}(s+2at)f-tD{}_0=(s+at)\left[\frac{1}{2}(1-\alpha )\frac{G(\theta )}{g(\theta )}+\theta \right](19)\\ t(D{}_0-af){}^2=2s(s+at){}^2\left[\frac{1}{2}(1-\alpha )\frac{{\rm M}(\tau )}{m(\tau )}+\tau \right](20)\end{array}$

解由式(19)、(20)构成的关于f和s的方程组, 可得规制经营模式下的停车费f_CG和停车场规模s_CG。

2.4   参数变化对停车场经营状况及社会福利影响

本节分析各参数变化对规制经营模式下的停车费f_CG、停车场规模s_CG、停车服务需求D_CG、私人停车管理公司的利润V_CG、政府对私人停车管理公司的转移支付T_CG以及社会总福利W_CG的影响。由于非线性方程组式(19)、(20)无法求得解析解, 本节采用数值模拟的方式来分析上述问题。为了使数值模拟具有一定的实际意义, 下面部分参数的设定参照了Tsai和Chu(2006)的参数设置^[13]。这里a为3, t为10, D₀为800, α为0.5, θ服从64~72的均匀分布, τ服从0.2~1.0的均匀分布。

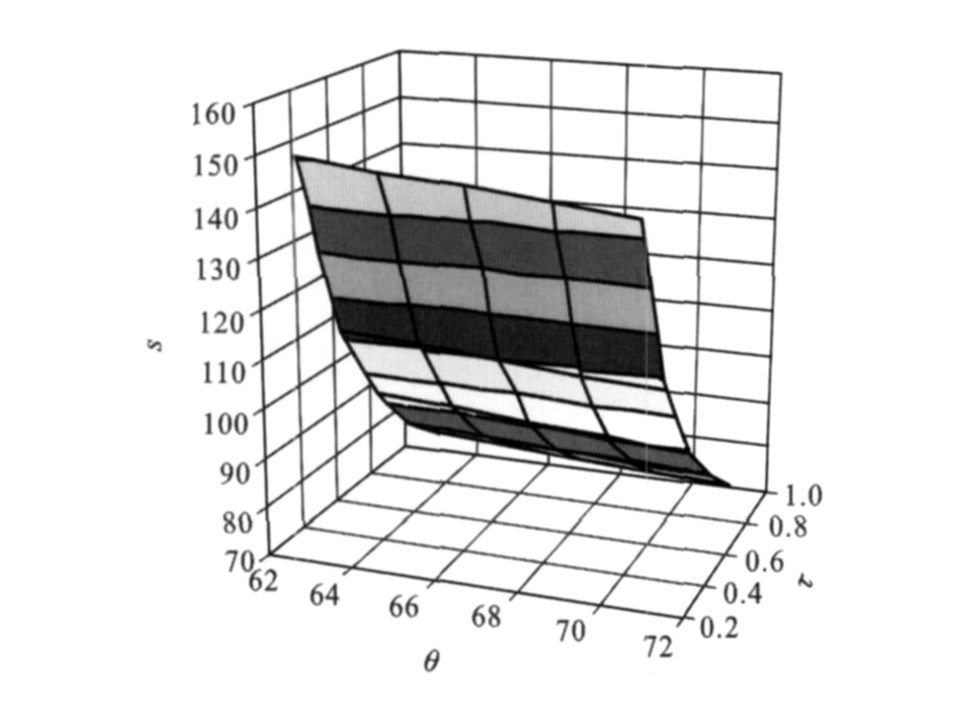
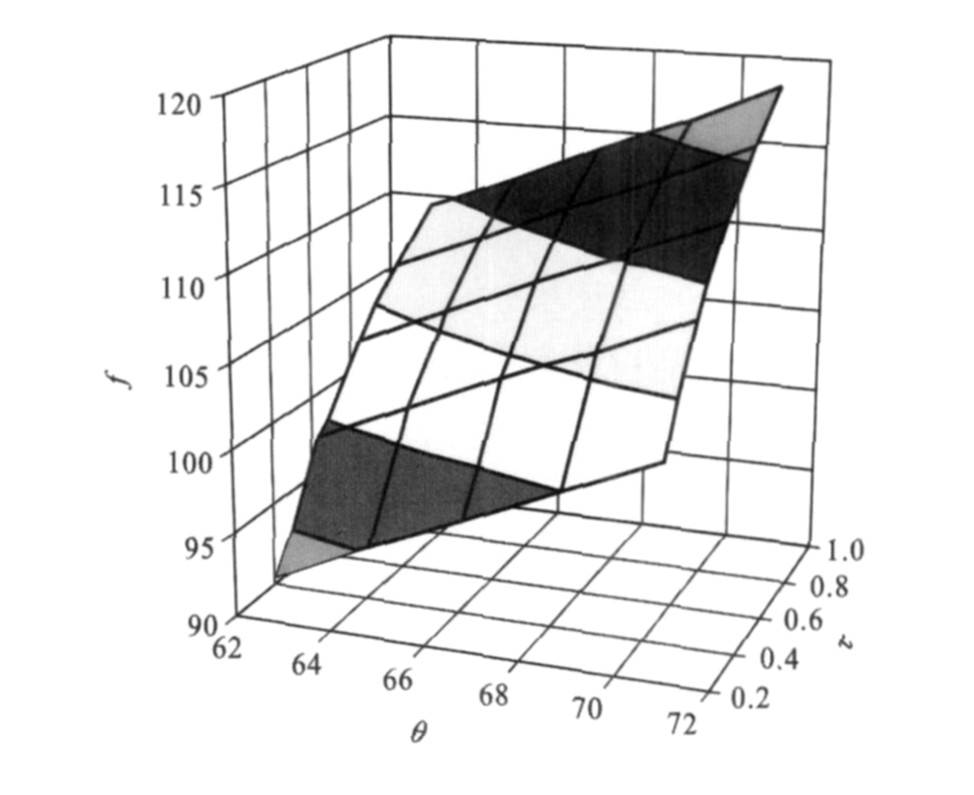
(1) 成本参数θ、τ同f_CG和s_CG之间的关系见

图 1、2, 由图 1、2可得如下结论。

图  1  不同θ和τ下的停车费

Figure  1.  Parking fees under different θ and τ

下载: 全尺寸图片 幻灯片

图  2  不同θ和τ下的停车场规模

Figure  2.  Parking scales under different θ and τ

下载: 全尺寸图片 幻灯片

结论1:规制经营模式下, 随着停车服务边际成本或停车场维护成本的增加, 停车费呈上升趋势, 而停车场的规模呈下降趋势。

(2) θ的变化给停车场经营及社会福利带来的变动见表 1, 可得如下结论。

结论2:规制经营模式下, 随着停车服务边际成本的增加, 停车服务需求、政府对私人停车管理公司的转移支付、私人停车管理公司的利润和社会总福利均呈下降趋势。

在参数的敏感性分析中, 为了单独突出各参数的影响, 分析当θ为70, τ为0.587 6时, 各参数的变化对停车场经营及社会福利的影响。选择上述2个特定数值是为了方便下文2种经营模式效果的比较。当然, θ和τ取其他数值时也可得到类似的结论。各参数敏感性的数值分析过程与表 1类似, 具体分析的结果见表 2。

表  1  θ的变化对D_CG、T_CG、V_CG和W_CG的影响

Table  1.  Effect of differentθon D_CG, T_CG, V_CGand W_CG

θ	DCG	TCG	VCG	WCG
64	372.07	33 151	4 078	30 403
65	368.97	32 753	3 569	30 264
66	365.88	32 352	3 059	30 128
67	362.79	31 943	2 549	29 994
68	359.70	31 528	2 039	29 862
69	356.62	31 108	1 529	29 733
70	353.54	30 682	1 020	29 606
71	350.47	30 250	510	29 482
72	347.40	29 814	0	29 360

下载: 导出CSV 

| 显示表格

表  2  各参数的增加对f_CG、s_CG、D_CG、T_CG、V_CG和W_CG的影响

Table  2.  Effect of increasing of each parameter on f_CG, s_CG, D_CG, T_CG, V_CGand W_CG

参数	fCG	sCG	DCG	TCG	VCG	WCG
θ	上升	下降	下降	下降	下降	下降
α	下降	上升	上升	上升	下降	上升
a	下降	下降	下降	下降	下降	下降
t	上升	上升	下降	下降	下降	下降

下载: 导出CSV 

| 显示表格

(3) α的变化给停车场经营及社会福利带来的变动见表 2, 可得如下结论。

结论3:规制经营模式下, 随着政府对私人停车管理公司关注程度的增加, 停车场规模、停车服务需求、政府对私人停车管理公司的转移支付和社会总福利呈上升趋势, 但停车费和私人停车管理公司的利润呈下降趋势。

(4) a的变化给停车场经营及社会福利带来的变动见表 2, 可得如下结论。

结论4:规制经营模式下, 随着停车服务需求量对价格的敏感程度的增加, 停车费、停车场规模、停车服务需求、政府对私人停车管理公司的转移支付、私人停车管理公司的利润和社会总福利均呈下降趋势。

(5) t的变化给停车场经营及社会福利带来的变动见表 2, 可得如下结论。

结论5:规制经营模式下, 随着用户等待时间成本的增加, 停车费、停车场规模呈上升趋势, 而停车服务需求、政府对私人停车管理公司的转移支付、私人停车管理公司的利润和社会总福利均呈下降趋势。

3.   竞争经营模式

3.1   基本假设

竞争经营模式服从2.1节中的假设2和假设4以及如下假设。

假设6:政府下属的公司参与停车场的经营, 因此, 政府完全掌握θ和τ的信息, 即此时对政府而言θ和τ是确定性变量, 而非随机变量。

假设6由引言中关于竞争经营模式的特点分析而得到, 表明此时政府由于参与停车场的实际经营管理, 对停车场的经营成本具有相当了解, 因此, 从信息效率的角度来看, 竞争经营模式应该优于规制经营模式。但由于此时部分停车场由营运效率较低的公有停车管理公司来经营, 因而从整体效率角度来看, 竞争经营模式未必优于规制经营模式。所以本文在第4小节将对各种情况下上述两种经营模式的效果进行比较分析。

假设7:私人停车管理公司的经营管理比公有停车管理公司更有效, 即私人停车管理公司提供停车服务的边际成本比公有停车管理公司的边际成本低。

关于公有企业和私营企业经营效率的比较问题, 经济学中大量的实证研究均表明, 私营企业的经营管理比公有企业更有效, 这与假设7是完全一致的。

3.2   博弈顺序

政府同私人停车管理公司的博弈顺序如下。

(1) 政府规定公有停车管理公司的经营面积和出租给私人停车管理公司的经营面积, 整个停车场由政府负责建设维护, 私人停车管理公司向政府交纳租赁费。

(2) 公有停车管理公司和私人停车管理公司进行同时行动的双寡头博弈, 其中政府的博弈策略为公有停车管理公司的停车费、公有停车管理公司的经营面积、出租给私人停车管理公司的经营面积, 而私人停车管理公司的博弈策略为私人停车管理公司的停车费。

(3) 用户在公有停车管理公司和私人停车管理公司之间进行选择。

3.3   停车费和停车场规模的确定

运用Tsai和Chu(2006)所提出的逆向归纳法^[13]来解决上述政府同私人停车管理公司之间的三阶段动态博弈。在下文中, 下标1表示公有停车管理公司, 下标2表示私人停车管理公司。首先考虑用户的决策问题, 当用户使用公有停车管理公司和私人停车管理公司所提供服务的广义价格相等时, 停车市场处于均衡状态, 即p₁=p₂, 即

$f{}_1+t{}_{1}D{}_1/s{}_1=f{}_2+t{}_{2}D{}_2/s{}_2$

运用式(1)得

$\begin{array}{l}D{}_1+D{}_2=D{}_0-a(f{}_1+t{}_{1}D{}_1/s{}_1)(21)\\ D{}_1+D{}_2=D{}_0-a(f{}_2+t{}_{2}D{}_2/s{}_2)(22)\end{array}$

由式(21)、(22)可得市场处于均衡状态下对公有停车管理公司和私人停车管理公司所提供服务的需求分别为

$\begin{array}{l}D{}_1=\frac{s{}_{1}s{}_2(f{}_2-f{}_1)+D{}_{0}t{}_{2}s{}_1-at{}_{2}f{}_{1}s{}_1}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(23)\\ D{}_2=\frac{s{}_{1}s{}_2(f{}_1-f{}_2)+D{}_{0}t{}_{1}s{}_2-at{}_{1}f{}_{2}s{}_2}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(24)\end{array}$

对于政府控制的公有停车管理公司, 其目标为社会总福利的最大化, 即

$\begin{array}{l}\underset{f{}_1,s{}_1,s{}_2}{{\displaystyle \max }}W{}_{\text{L}\text{G}}={\displaystyle {\int }_0^{D{}_1}p}\text{d}x-c{}_1-t{}_{1}D{}_1^2/s{}_1+{\displaystyle {\int }_0^{D{}_2}p}\text{d}x-\\ f{}_{2}D{}_2-t{}_{2}D{}_2^2/s{}_2+R+\alpha (f{}_{2}D{}_2-c{}_2-R)(25)\end{array}$

R=τs₂²

c₁=θ₁D₁+τ(s₁²+s₂²)

c₂=θ₂D₂

上述优化问题的目标函数中, ∫ ${}_0^{D{}_1}$ pdx-c₁-t₁D ${}_1^2$ /s₁为公有停车管理公司服务产生的消费者剩余减去其营运成本、停车场的维护成本以及用户等待时间成本的总和; ∫ ${}_0^{D{}_2}$ pdx-f₂D₂-t₂D ${}_2^2$ /s₂为私人停车管理公司服务产生的消费者剩余减去其营运成本和用户等待时间成本总和; R为租赁费; f₂D₂-c₂-R为私人停车管理公司的利润。

整理式(25)可得

$\begin{array}{l}\underset{f{}_1,s{}_1,s{}_2}{{\displaystyle \max }}W{}_{\text{L}\text{G}}={\displaystyle {\int }_0^{D{}_1+D{}_2}p}\text{d}x-c{}_1-t{}_{1}D{}_1^2/s{}_1-\alpha c{}_2-\\ t{}_{2}D{}_2^2/s{}_2-(1-\alpha )f{}_{2}D{}_2+(1-\alpha )R(26)\end{array}$

对于私人停车管理公司, 其目标为利润最大化, 即

$\underset{f{}_2}{{\displaystyle \max }}V{}_{\text{L}\text{G}}=f{}_{2}D{}_2-c{}_2-R(27)$

式(26)、(27)的一阶条件为

$\begin{array}{l}\left(\frac{D{}_0}{a}-\frac{D{}_1+D{}_2}{a}\right)\left(\frac{\partial D{}_1}{\partial f{}_1}+\frac{\partial D{}_2}{\partial f{}_1}\right)-\theta {}_1\frac{\partial D{}_1}{\partial f{}_1}-\frac{2t{}_{1}D{}_1}{s{}_1}\frac{\partial D{}_1}{\partial f{}_1}-\\ \alpha \theta {}_2\frac{\partial D{}_2}{\partial f{}_1}-\frac{2t{}_{2}D{}_2}{s{}_2}\frac{\partial D{}_2}{\partial f{}_1}-(1-\alpha )f{}_2\frac{\partial D{}_2}{\partial f{}_1}=0(28)\\ D{}_2+f{}_2\frac{\partial D{}_2}{\partial f{}_2}-\theta {}_2\frac{\partial D{}_2}{\partial f{}_2}=0(29)\\ \left(\frac{D{}_0}{a}-\frac{D{}_1+D{}_2}{a}\right)\left(\frac{\partial D{}_1}{\partial s{}_1}+\frac{\partial D{}_2}{\partial s{}_1}\right)-\theta {}_1\frac{\partial D{}_1}{\partial s{}_1}-2\tau s{}_1-\\ t{}_1\left(\frac{2D{}_1}{s{}_1}\frac{\partial D{}_1}{\partial s{}_1}-\frac{D{}_1^2}{s{}_1^2}\right)-2D{}_2\frac{t{}_2}{s{}_1}\frac{\partial D{}_2}{\partial s{}_1}-\\ \alpha \theta {}_2\frac{\partial D{}_2}{\partial s{}_1}-(1-\alpha )f{}_2\frac{\partial D{}_2}{\partial s{}_1}=0(30)\\ \left(\frac{D{}_0}{a}-\frac{D{}_1+D{}_2}{a}\right)\left(\frac{\partial D{}_1}{\partial s{}_2}+\frac{\partial D{}_2}{\partial s{}_2}\right)-\theta {}_1\frac{\partial D{}_1}{\partial s{}_2}-2\tau s{}_2-\\ 2D{}_1\frac{t{}_1}{s{}_1}\frac{\partial D{}_1}{\partial s{}_2}-t{}_2\left(\frac{2D{}_2}{s{}_2}\frac{\partial D{}_1}{\partial s{}_2}-\frac{D{}_2^2}{s{}_2^2}\right)-\alpha \theta {}_2\frac{\partial D{}_2}{\partial s{}_2}+\\ 2(1-\alpha )\tau s{}_2-(1-\alpha )f{}_2\frac{\partial D{}_2}{\partial s{}_2}=0(31)\\ \frac{\partial D{}_1}{\partial f{}_1}=\frac{-s{}_{1}s{}_2-at{}_{2}s{}_1}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(32)\\ \frac{\partial D{}_1}{\partial f{}_2}=\frac{\partial D{}_2}{\partial f{}_1}=\frac{s{}_{1}s{}_2}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(33)\\ \frac{\partial D{}_2}{\partial f{}_2}=\frac{-s{}_{1}s{}_2-at{}_{1}s{}_2}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(34)\\ \frac{\partial D{}_1}{\partial s{}_1}=\frac{D{}_1}{s{}_1}-\frac{D{}_{1}t{}_2}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(35)\\ \frac{\partial D{}_1}{\partial s{}_2}=\frac{s{}_1(f{}_2-f{}_1)-D{}_{1}t{}_1}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(36)\\ \frac{\partial D{}_2}{\partial s{}_1}=\frac{s{}_2(f{}_1-f{}_2)-D{}_{2}t{}_2}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(37)\\ \frac{\partial D{}_2}{\partial s{}_2}=\frac{D{}_2}{s{}_2}-\frac{D{}_{2}t{}_1}{t{}_{1}s{}_2+t{}_{2}s{}_1+at{}_{1}t{}_2}(38)\end{array}$

将式(32)~(38)代入式(28)~(31), 求解由式(28)~(31)组成的关于得到关于f₁、f₂、s₁、s₂的方程组, 可得竞争经营模式下公有停车管理公司的停车费f_LG¹、私人停车管理公司的停车费f_LG²、公有停车管理公司的经营面积s_LG¹和私人停车管理公司的经营面积s_LG²。

3.4   参数变化对停车场经营状况及社会福利影响

采用数值模拟的方式来分析各参数变化对公有停车管理公司的停车费f_LG¹、私人停车管理公司的停车费f ${}_{\text{L}\text{G}}^2$、公有停车管理公司的经营面积s_LG¹、私人停车管理公司的经营面积s_LG²、停车场总规模s_LG、停车服务总需求D_LG、私人停车管理公司的利润V_LG以及社会总福利W_LG的影响。为了便于比较, 本节的参数设定同2.4节, 各参数敏感性的数值分析过程也与表 1类似, 具体的分析结果见表 3。

$\begin{array}{l}s{}_{\text{L}\text{G}}=s{}_{\text{L}\text{G}}^1+s{}_{\text{L}\text{G}}^2\\ D{}_{\text{L}\text{G}}=D{}_1+D{}_2\end{array}$

表  3  各参数的变化对f_LG¹、f ${}_{\mathbf{L}\mathbf{G}}^2$、s_LG¹、s_LG²、s_LG、D_LG、V_LG和W_LG的影响

Table  3.  Effect of increasing of each parameter on f ${}_{\mathbf{L}\mathbf{G}}^1$, f ${}_{\mathbf{L}\mathbf{G}}^2$, s_LG¹, s_LG², s_LG, D_LG, V_LGand W_LG

参数	f${}_{\text{L}\text{G}}^1$	f${}_{\text{L}\text{G}}^2$	sLG1	s${}_{\text{L}\text{G}}^2$	LGs	DLG	VLG	WLG
θ2	上升	上升	上升	下降	下降	下降	下降	下降
α	上升	上升	不定	下降	下降	下降	上升	不定
a	下降	下降	下降	下降	下降	下降	下降	下降
t1、t2	上升	上升	上升	上升	上升	下降	上升	下降

下载: 导出CSV 

| 显示表格

(1) θ₂的变化给停车场经营及社会福利带来的变动见表 3, 可得如下结论。

结论6:竞争经营模式下, 随着私人停车管理公司边际成本的增加, 公有停车管理公司和私人停车管理公司的停车费均呈上升趋势, 公有停车管理公司的经营面积呈上升趋势, 私人停车管理公司的经营面积呈下降趋势, 但停车场总规模呈下降趋势, 此外, 停车服务总需求、私人停车管理公司的利润以及社会总福利均呈下降趋势。

同样为了单独突出各参数的影响, 同2.4节中一样, 分析当θ₂为70, τ为0.587 6时, 各参数的变化对停车场经营及社会福利的影响。当然, 上述参数取其他数值时也可得到类似的结论。

(2) α的变化给停车场经营及社会福利带来的变动见表 3, 可得如下结论。

结论7:竞争经营模式下, 随着政府对私人停车管理公司的关注程度的增加, 公有停车管理公司的停车费和私人停车管理公司的利润呈上升趋势, 私人停车管理公司的经营面积、停车场总规模和停车服务总需求呈下降趋势, 但私人停车管理公司的停车费、公有停车管理公司的经营面积和社会总福利的变化趋势不定。

(3) a的变化给停车场经营及社会福利带来的变动见表 3, 可得如下结论。

结论8:竞争经营模式下, 随着停车服务需求量对价格的敏感程度的增加, 公有停车管理公司和私人停车管理公司的停车费、公有停车管理公司和私人停车管理公司的经营面积、停车场总规模、停车服务总需求、私人停车管理公司的利润以及社会总福利均呈下降趋势。

(4) t的变化给停车场经营及社会福利带来的变动见表 3, 可得如下结论。

结论9:竞争经营模式下, 随着用户等待时间成本的增加, 公有停车管理公司和私人停车管理公司的停车费、公有停车管理公司和私人停车管理公司的经营面积、停车场总规模和私人停车管理公司的利润均呈上升趋势, 而停车服务总需求和社会总福利呈下降趋势。

4.   经营模式的比较

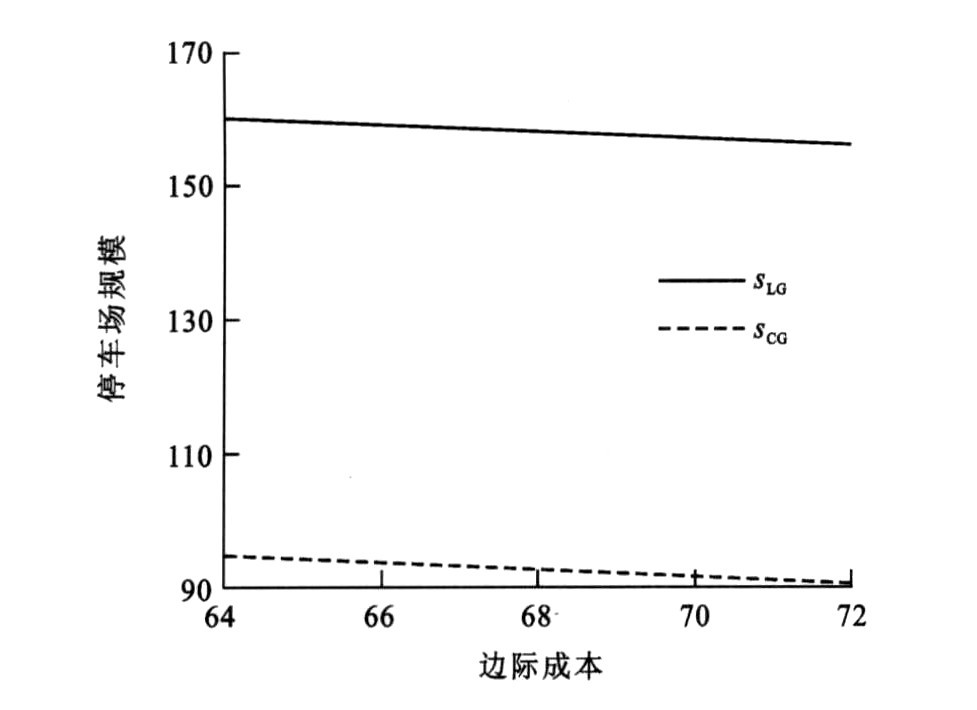
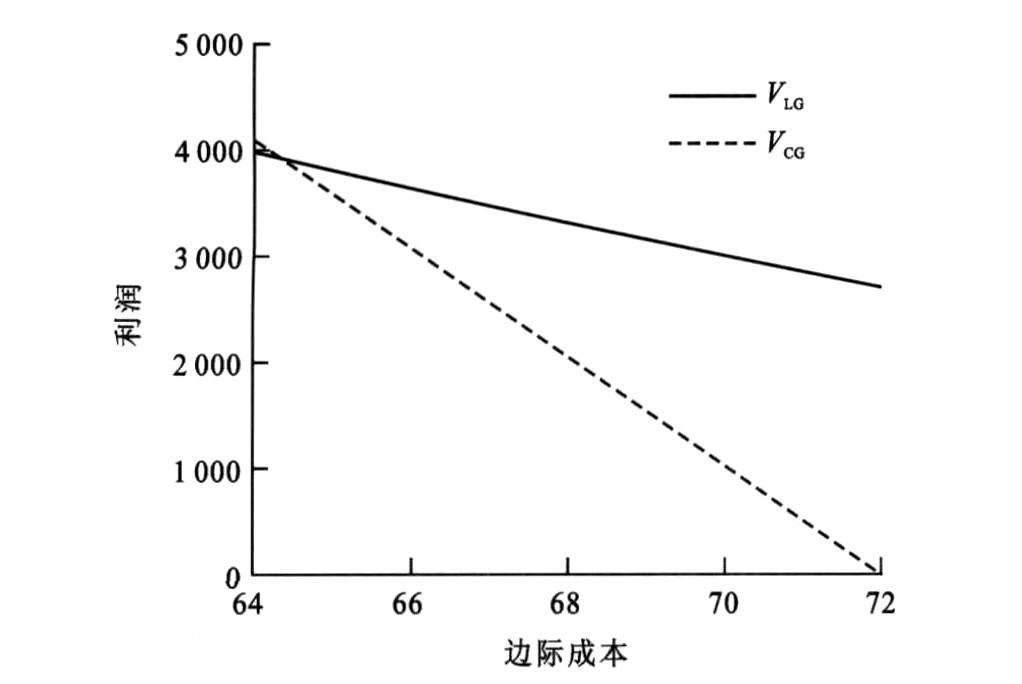
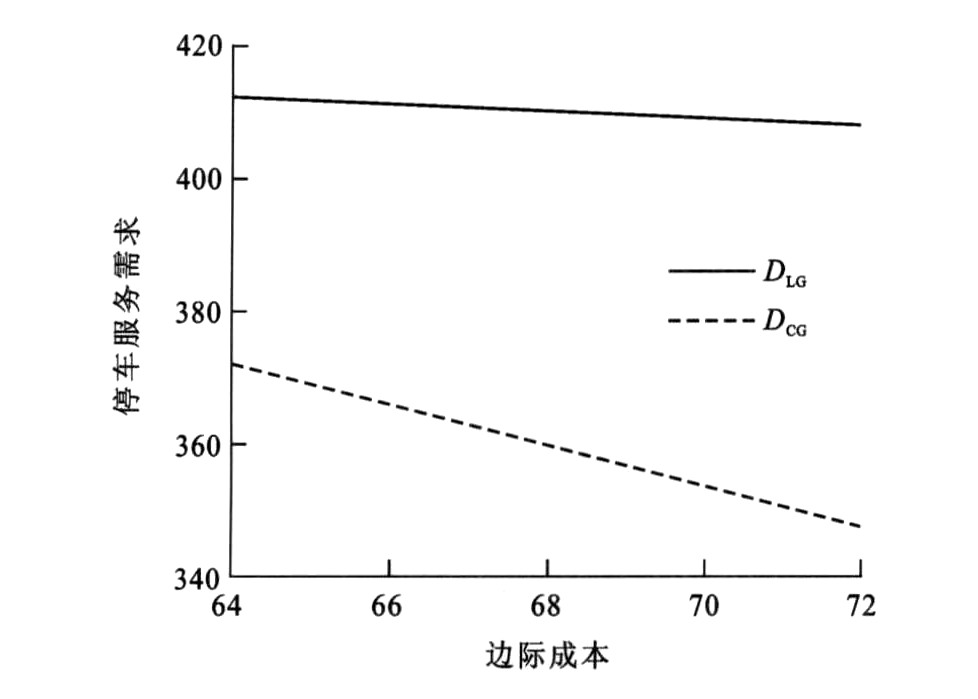
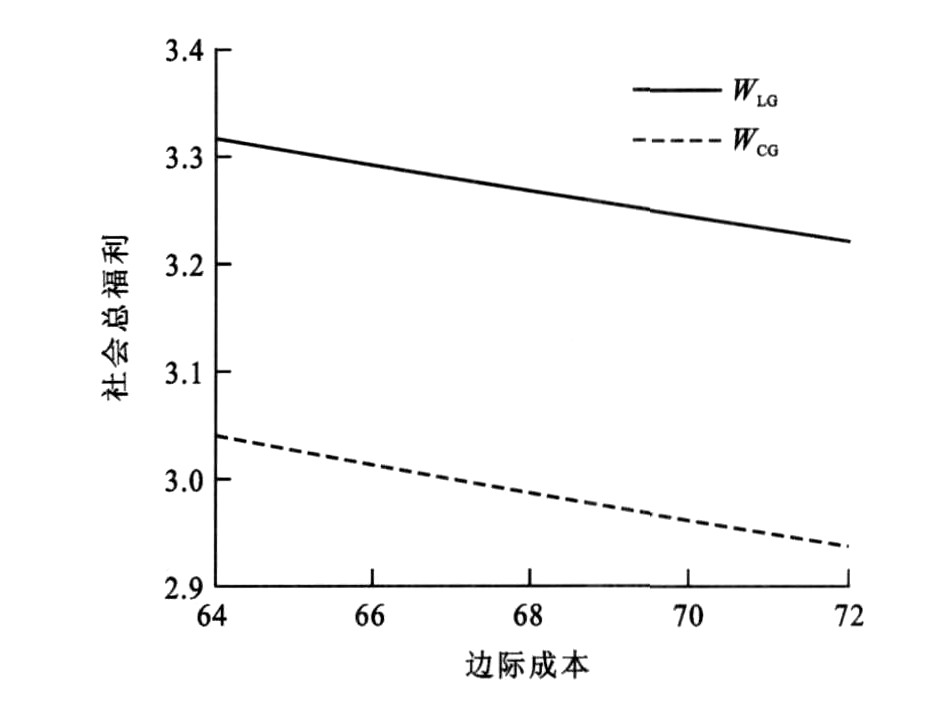
为了分析经营模式的改变对停车场经营及社会福利的影响, 本文就各参数的变化对两种经营模式下停车费、私人停车管理公司的利润、停车场总规模、停车服务总需求和社会总福利进行对比, 其中图 3~7反映了停车服务的边际成本变化的情况下两种经营模式的对比, 其他参数变动时两种经营模式的对比分析过程与之类似, 其结果总结见表 4, 通过表 4可得如下结论。

图  3  不同θ、θ₂取值下f_LG¹、f_LG²和f_CG的比较

Figure  3.  Comparison of f_LG¹, f_LG² and f_CG with different θ, θ₂

下载: 全尺寸图片 幻灯片

表  4  规制经营模式和竞争经营模式的比较

Table  4.  Comparison of regulation operation mode and competition operation mode

参数	停车费	私人停车管理公司的利润	停车场总规模	停车服务总需求	社会总福利
θ、θ2	fLG1最小, fLG2和fCG比较结果不定	VCG < VLG	sCG < sLG	DCG < DLG	WCG < WLG
α	fLG1、fLG2和fCG比较结果不定	当α较大时, VCG < VLG	sCG < sLG	DCG < DLG	WCG < WLG
a	fLG1、fLG2和fCG比较结果不定	VCG < VLG	sCG < sLG	DCG < DLG	WCG≈WLG
t	fCG > fLG2 > fLG1	VCG < VLG	sCG < sLG	DCG < DLG	WCG≈WLG

下载: 导出CSV 

| 显示表格

图  4  不同θ、θ₂取值下s_CG和s_LG的比较

Figure  4.  Comparison of s_CG and s_LG with different θ, θ₂

下载: 全尺寸图片 幻灯片

图  5  不同θ、θ₂取值下V_CG和V_LG的比较

Figure  5.  Comparison of V_CG and V_LG with different θ, θ₂

下载: 全尺寸图片 幻灯片

图  6  不同θ、θ₂取值下D_CG和D_LG的比较

Figure  6.  Comparison of D_CG and D_LG with different θ, θ₂

下载: 全尺寸图片 幻灯片

图  7  不同θ、θ₂取值下W_CG和W_LG的比较

Figure  7.  Comparison of W_CG and W_LG with different θ, θ₂

下载: 全尺寸图片 幻灯片

(1) 停车服务的边际成本对经营模式的影响

结论10:比较两种经营模式可见, 不论停车服务的边际成本如何变化, 竞争经营模式下停车场总规模、停车服务总需求和社会总福利高于规制经营模式下; 大多数情况下私人停车管理公司的利润在竞争经营模式下较高; 而竞争经营模式下公有停车管理公司的停车费是最低的。

(2) 政府对私人停车管理公司的关注程度对经营模式的影响

结论11:比较两种经营模式可见, 不论政府对私人停车管理公司的关注程度如何变化, 竞争经营模式下停车场总规模和社会总福利高于规制经营模式下; 大多数情况下停车服务总需求在竞争经营模式下较高; 当政府对私人停车管理公司较为关注时竞争经营模式下私人停车管理公司的利润较高; 但经营模式对停车费的影响不定。

(3) 停车服务需求量对价格的敏感程度对经营模式的影响

结论12:比较两种经营模式可见, 不论停车服务需求量对价格的敏感程度如何变化, 竞争经营模式下停车场总规模、私人停车管理公司的利润和停车服务总需求高于规制经营模式下; 但两种经营模式下社会总福利相差不大; 而经营模式对停车费的影响不定。

(4) 用户等待时间成本对经营模式的影响

结论13:比较两种经营模式可见, 不论用户的等待时间成本如何变化, 竞争经营模式下停车场总规模、停车服务总需求、私人停车管理公司的利润和社会总福利高于规制经营模式下; 而竞争经营模式下公有停车管理公司的停车费是最低的。

5.   结语

本文讨论了规制经营和竞争经营两种公共停车场管理模式下的停车费和停车场规模的优化模型, 得出了公共停车场最优停车费和规模的制定准则, 分析了各因素对最优停车费和规模的影响。通过对两种模式下公共停车场的经营状况和社会福利的比较得知: 经营模式对停车费的影响不定; 竞争经营模式下停车场的规模较大, 大约较规制经营模式下大94.21%, 因此竞争经营模式有利于停车场的建设; 私人停车管理公司偏好竞争经营模式, 因为在该模式下私人停车管理公司的利润较高, 大约较规制经营模式下高67.13%;竞争经营模式下停车服务总需求较高, 大约较规制经营模式下大36.70%;竞争经营模式下社会福利较高, 大约较规制经营模式下高41.34%。从上述结论可见, 竞争经营模式对停车场的经营管理和社会福利较为有利, 因此, 这种经营模式应成为今后公共停车场的主要管理方式。

当然, 本文的研究还存在一些不足, 例如没有考虑公有和私人停车管理公司之间可能存在的合谋对停车费、停车场规模和经营模式的影响, 又如没有考虑停车服务需求的随机变动所带来的影响, 这些将是今后进一步研究的方向。