Relation between accident rate and horizontal alignment for mountain highway
-
摘要: 统计了2条山区公路的交通事故数据与平面线形数据, 采用角度变化率作为平面线形的表征参数, 对样本路段区间内的事故率与角度变化率进行回归分析, 分别计算了当前样本路段向前0.25、0.50、0.75、1.00、1.50km等多个计算区间上的平均角度变化率。对角度变化率进行二次处理, 利用最小二乘法拟合了事故率与角度变化率之间的曲线关系。分析结果表明: 路段1、2区间内的事故率与角度变化率的拟合判定系数较低, 分别为0.414 2和0.120 8;在当前样本路段向前0.50km的计算区间上, 事故率与平均角度变化率的正二次抛物线关系均最明显, 拟合判定系数分别为0.966 1和0.790 8;当平均角度变化率大约在0.002 0(°)·km-1时, 事故率最低。Abstract: The traffic accident data and horizontal alignment data of two mountain highways were collected, the curvature change rate was regarded as the characteristic parameter of horizontal alignment, the regression analysis between accident rate and curvature change rate on current sample section was carried out, and the average curvature change rates of those several calculation intervals were respectively calculated, which were 0.25, 0.50, 0.75, 1.00 and 1.50 km upward of current sample section.The secondary treatment on the curvature change rate was carried out, and the relations between the accident rates and the curvature change rates were fitted by using least square method.Analysis result shows that the fitting determination coefficients between the accident rates and the curvature change rates on sections 1 and 2 are lower, are about 0.414 2 and 0.120 8 respectively.While on the calculation intervals that are 0.5 km upward of current sample sections, their positively secondary parabolic relations both are the most significantly, and the fitting determination coefficients are 0.966 1 and 0.790 8 respectively.While the average curvature change rate is about 0.002 0(°)·km-1, the accident rate is lowest.
-
0. 引言
道路交通事故统计资料表明, 道路线形是影响事故发生的重要因素之一[1-3], 道路线形对事故的影响主要体现在纵面线形与平面线形方面[4-5]。相对于纵面线形, 平面线形更加复杂, 这主要是因为其不仅包含圆曲线、直线与缓和曲线, 而且描述平面线形的参数也比较多, 如圆曲线半径、缓和曲线长度、直线长度与平面线形转角等[6-7]。
平面线形是常用的道路线形, 可以调整路线前进的方向, 以适应地形、地物的变化, 但车辆在弯道上行驶时要受到离心力的作用, 弯道离心力的大小又与弯道的半径和车辆的行驶速度有关[8]。如果车速过快, 加上驾驶员的偶尔疏忽、车辆质心偏高与路面条件不好等均可能导致在弯道上行驶的车辆发生危险[9-10]。邹健将重庆市几条主干道的交通事故率与弯道个数的关系绘成散点图, 分析发现单位长度的弯道个数(即弯道密度)与交通事故率有很强的相关关系, 判定系数达到了0.99, 弯道密度增大或减小都会导致事故率上升, 弯道密度随地理环境和道路等级的变化而变化[11]; Vogt等在1991年提出了一个事故预测模型用以预测平面线形上的事故数量, 认为平面线形路段上的事故数量随着曲线长度与曲率的增大而增大, 随着缓和曲线的设置与行车道宽度的增大而减少[12]; Glennon等以理论假设为基础, 利用数据统计分析提出了一个平面线形事故预测模型, 发现平面线形路段的预测事故数是平直路段事故数与曲线特征系数的组合, 与道路曲率与交通量指标成正比[13]; 景天然对道路要素与事故之间的关系进行了研究, 得到了道路平均事故率与平面线形半径的关系[14]; 黄进等收集了湖南某国道的事故数据和线形资料, 对312个圆曲线路段的数据进行拟合, 得到了事故数量与圆曲线长度、曲线角度与缓和曲线长度的关系[15]。
以上这些研究分别以不同平面线形评价指标为研究对象, 分析了路段事故率与平面线形指标之间的关系。然而, 表征平面线形特征的指标众多, 不同指标对事故的影响程度也不同, 采用单一指标研究平面线形与事故率之间的关系, 不能深入挖掘平面线形整体特征与事故率之间的关系, 存在局限性。针对此类问题, 本文通过对实际道路平面线形指标和既往事故数据的采集和分析, 探讨不同路段事故率与角度变化率的关系。
1. 平面线形参数的选择与均值化
在平面线形上, 由地形引起路线的变化体现在路线的方位角上[16-17], 道路曲线偏角的大小表征了路线的弯曲程度。Fitzpatrick等在研究车辆运行速度与平面线形要素的相互关系时, 提出了平面线形安全评价方法[18-19]
式中: R为角度变化率((°)·km-1), 是相似特征路段上每单位长度的角度变化之和; L为路段总长度(m); Q为相似特征连续路段内圆曲线i的长度(m); S为相邻缓和曲线j的长度(m); r为圆曲线i的半径(m)。
由式(1)可知, 角度变化率是路段长度内平均单位长度的偏角变化, 包含了所研究路段内圆曲线长度、圆曲线半径、缓和曲线长度与直线段长度, 并且考虑到了相邻曲线间的相互作用, 反映了平面线形的总体特征。采用式(1)对2条路段的平面线形参数进行计算, 得到事故率y与角度变化率R之间的散点分布, 基于最小二乘法对事故率与角度变化率进行二次多项式拟合, 过程如下[20-23]。
令事故率与角度变化率之间的二次多项式为
式中: a、b、c均为待定系数。
统计所有事故率与角度变化率的数据总数, 记为m, 参考式(2), 误差方程为
式中: α为正整数, 且α∈[1, m];ωα为误差值; yα为统计得到的事故数据; Rα为yα对应的角度变化率。
根据残差平方和最小条件, 求解系数a、b、c的最优解, 并计算拟合精度。然而如果直接采用式(1)~(3)计算事故率与角度变化率的关系, 拟合精度不高, 主要原因在于所选取的样本长度为各个平面线形长度, 而单个样本长度容易受到纵面线形、构造物(桥梁、隧道)等的影响, 为达到平衡和淡化其他因素对事故率的影响, 突出事故率与角度变化率的关系, 本文使用样本均值化方法对角度变化率进行二次处理, 并重新使用最小二乘法进行二次曲线拟合, 过程如下。
Step 1 以0.001 0(°)·km-1为单位对原样本进行划分, 如果某范围内的原样本过多时, 采用0.000 5(°)·km-1为单位进行划分, 划分出n个新样本, 分别为R1、R2、…、Rn。
Step 2 从0.000 1(°)·km-1开始, 分段计算区间内的事故率指标值
式中: yβ为对应角度变化率区间β内的事故率; tγ为β事故数区间第γ个事故数量; p为β区间总的事故数量。
Step 3 为考察相邻路段线形对样本事故率的影响, 本文向前延伸样本长度, 即分别对当前样本路段向前0.25、0.50、0.75、1.00、1.50km的平均事故率与角度变化率之间的关系进行统计分析, 计算方法与式(4)相同。
Step 4 使用最小二乘法对Step 2、3得到的事故率与角度变化率进行二次多项式拟合, 分别得到拟合式与拟合精度。
2. 拟合结果分析
路段1为山岭重丘区二级公路, 双向二车道, 设计行车速度为40km·h-1, 路基宽度为12m, 路段长度为8.8km; 弯多且急, 累计弯道数为22个, 半径小于200m的弯道数为13个, 转角大于100°的弯道数有2个, 弯道密度为2.54个·km-1; 道路一侧为峭壁, 另一侧为深沟, 交通事故频发。在24个月的统计期内, 路段1上共发生事故108起, 造成29人死亡, 110人受伤, 部分事故分布统计数据见表 1。
表 1 路段1平面线形参数与事故分布Table 1. Horizontal alignment parameters and accident distribution of section 1
路段2为二级公路, 路段长度为33.2km; 有一段约长度为9.0km的峡谷地带, 道路坡陡弯急, 沿线地势险要, 分布有5个隧道; 另有一段长度为6.8km的多弯道路段, 分布了29个弯道, 弯道密度为4.26个·km-1, 有一段距离较长的连续的小半径弯道是事故的高发路段。在29个月的统计期内, 该路段共发生事故437起, 造成62人死亡, 242人受伤, 部分事故分布统计数据见表 2。
表 2 路段2平面线形参数与事故分布Table 2. Horizontal alignment parameters and accident distribution of section 2
根据式(4)对所有样本区间进行计算, 依次得到每个平面线形区间内的角度变化率以及当前样本路段向前0.25、0.50、0.75、1.00、1.50km等计算区间(分别计为A、B、C、D、E五个区间)上的平均角度变化率, 部分数据分别见表 3、4。
表 3 路段1事故数量与角度变化率Table 3. Accident mumbers and curvature change rates of section 1
表 4 路段2事故数量与角度变化率Table 4. Accident numbers and curvature change rates of section 2
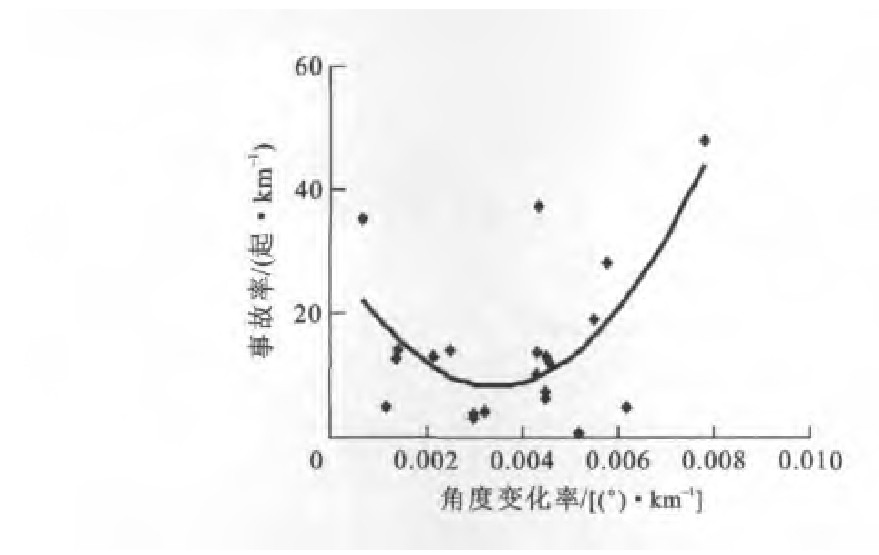
由表 3、4计算路段1、2区间内的事故率与角度变化率的二次多项式拟合关系, 结果分别见图 1、2。
图 1 路段1事故率与角度变化率的关系Figure 1. Relation between accident rate and curvature change rate of section 1
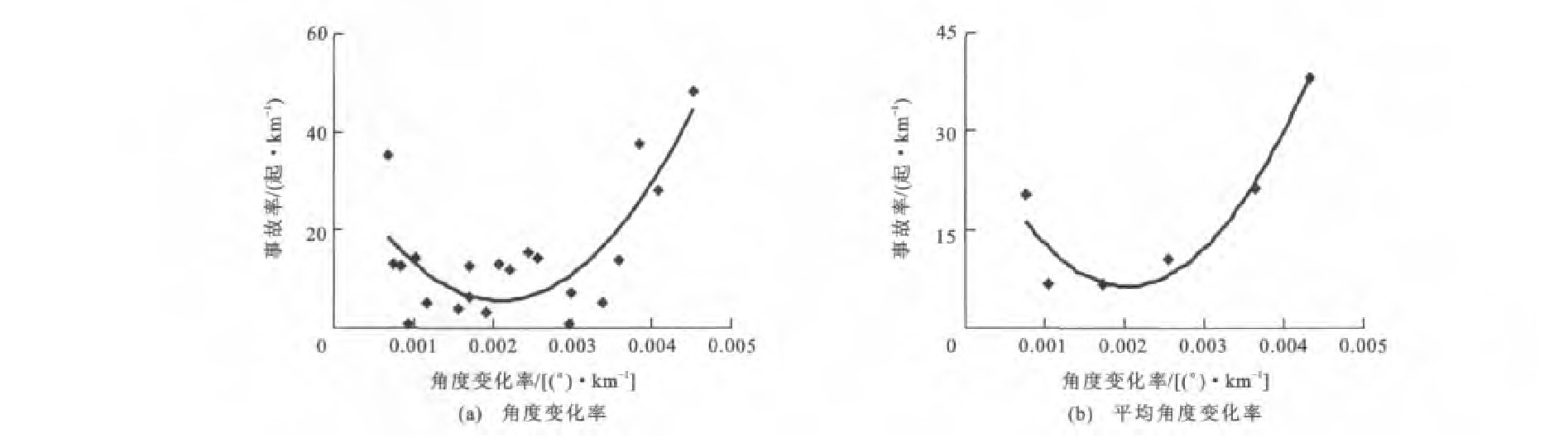
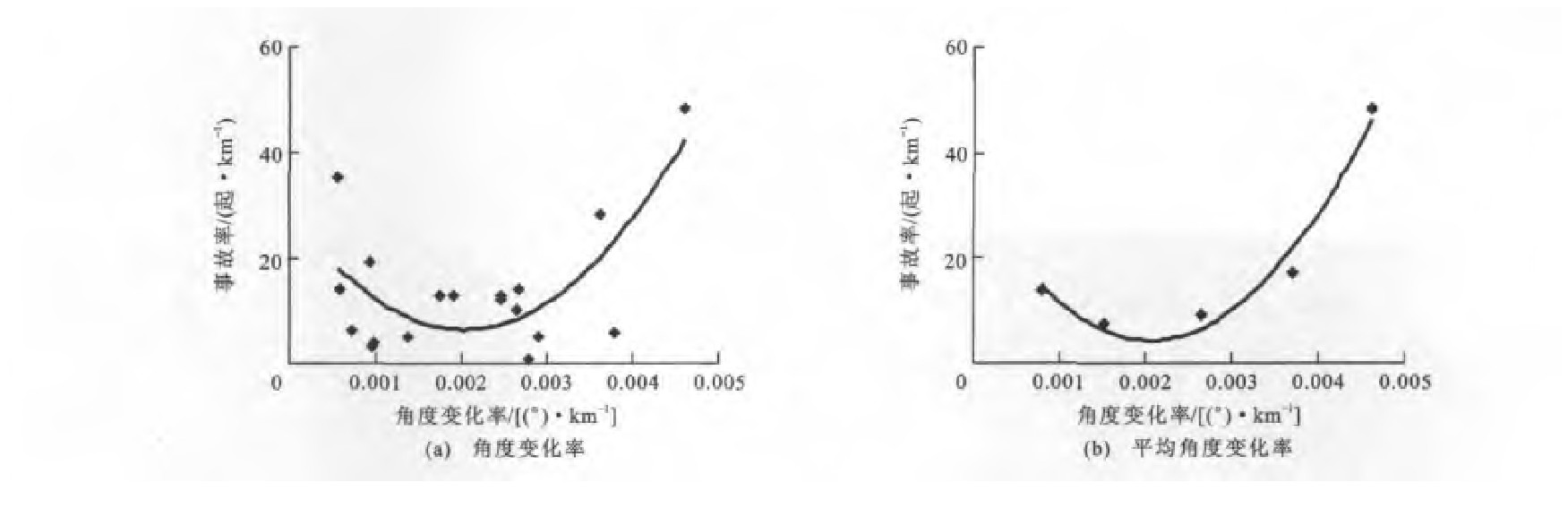
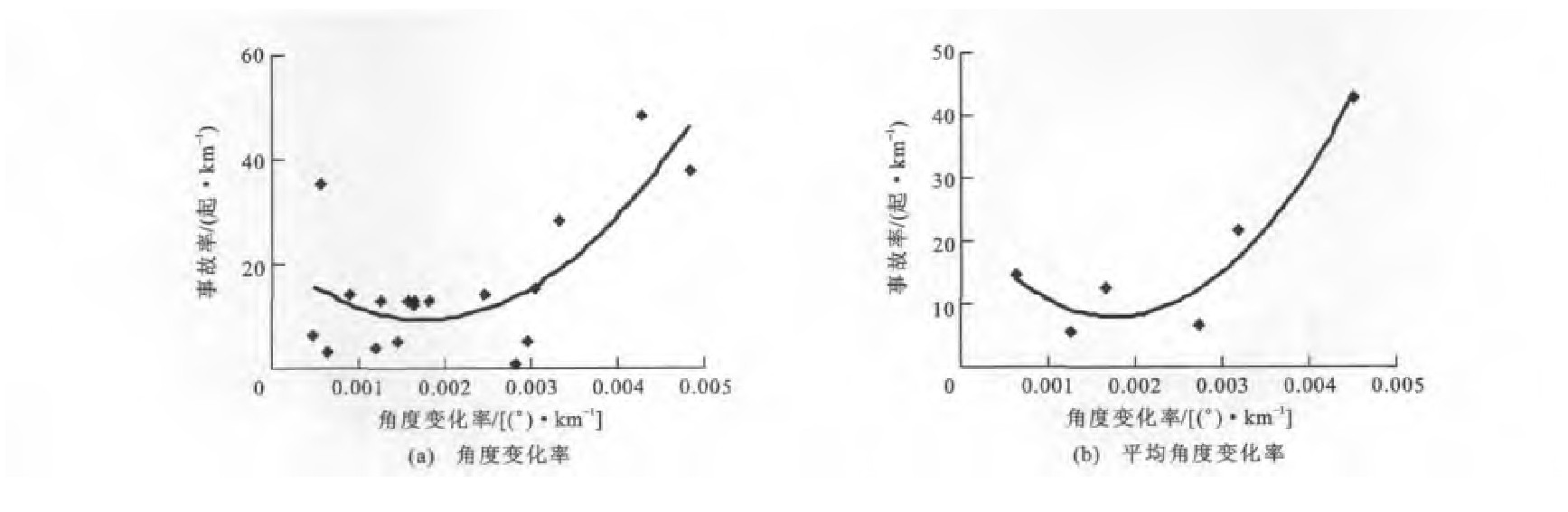
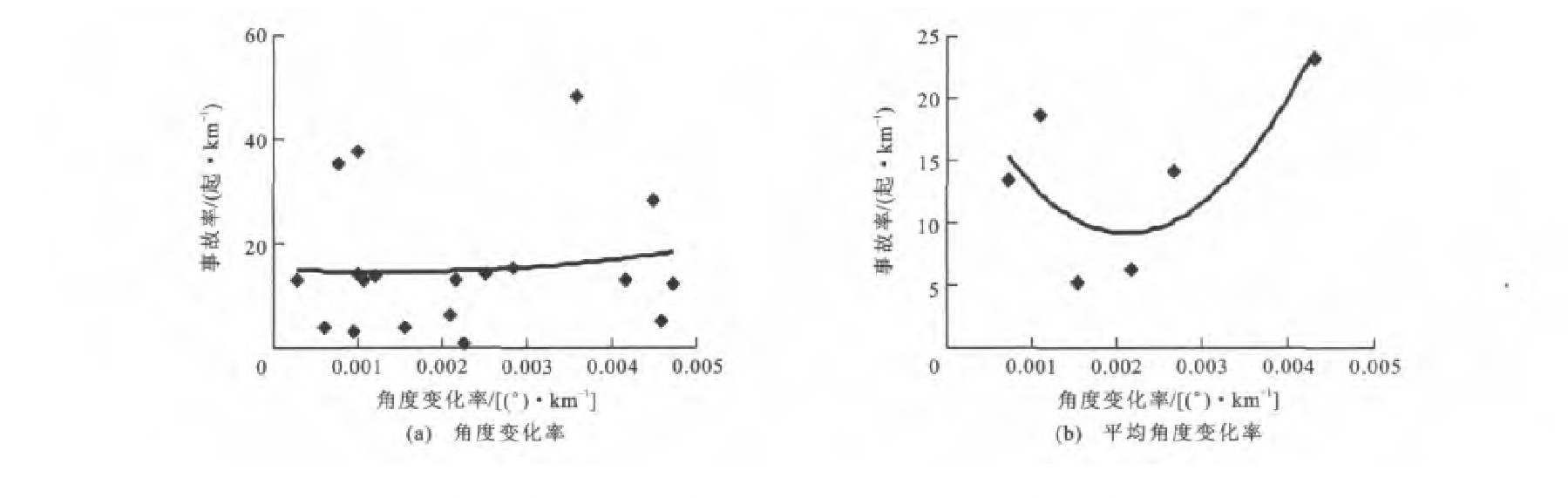
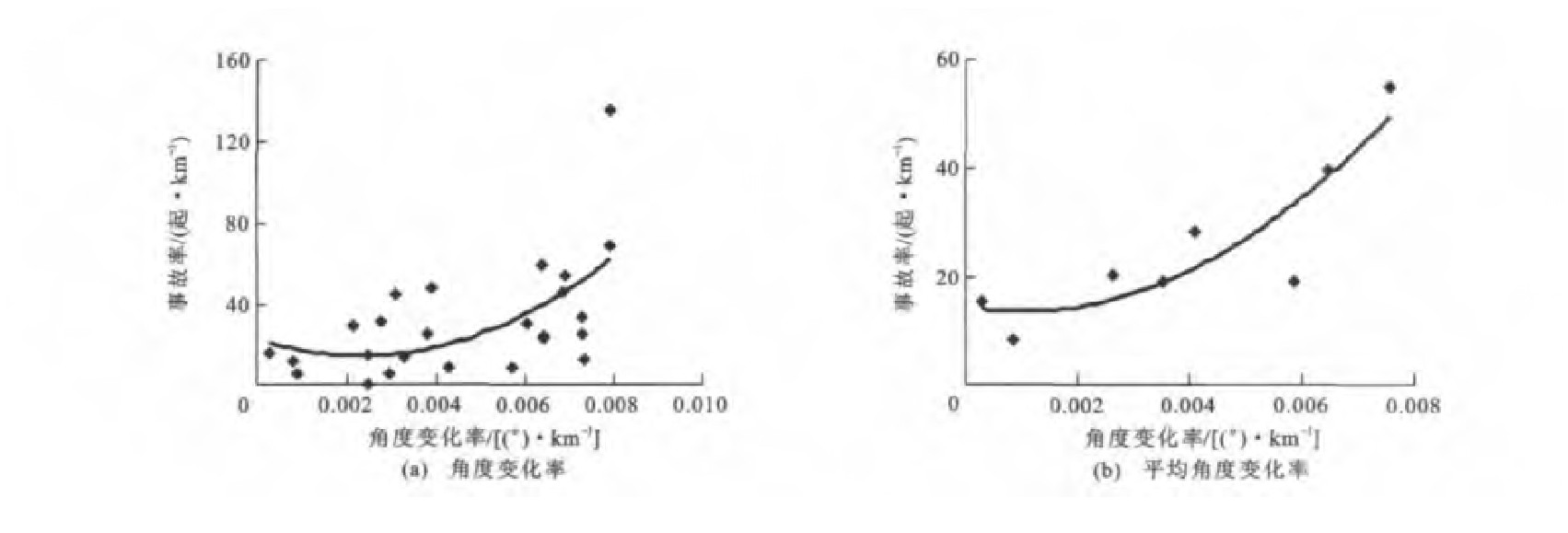
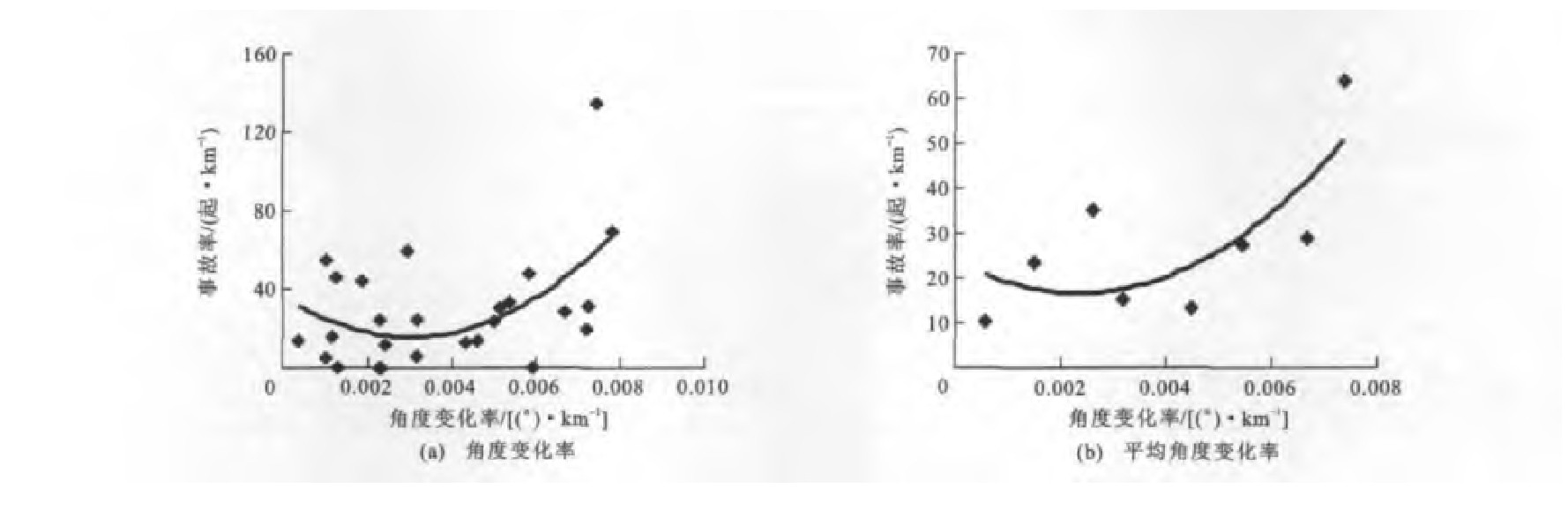
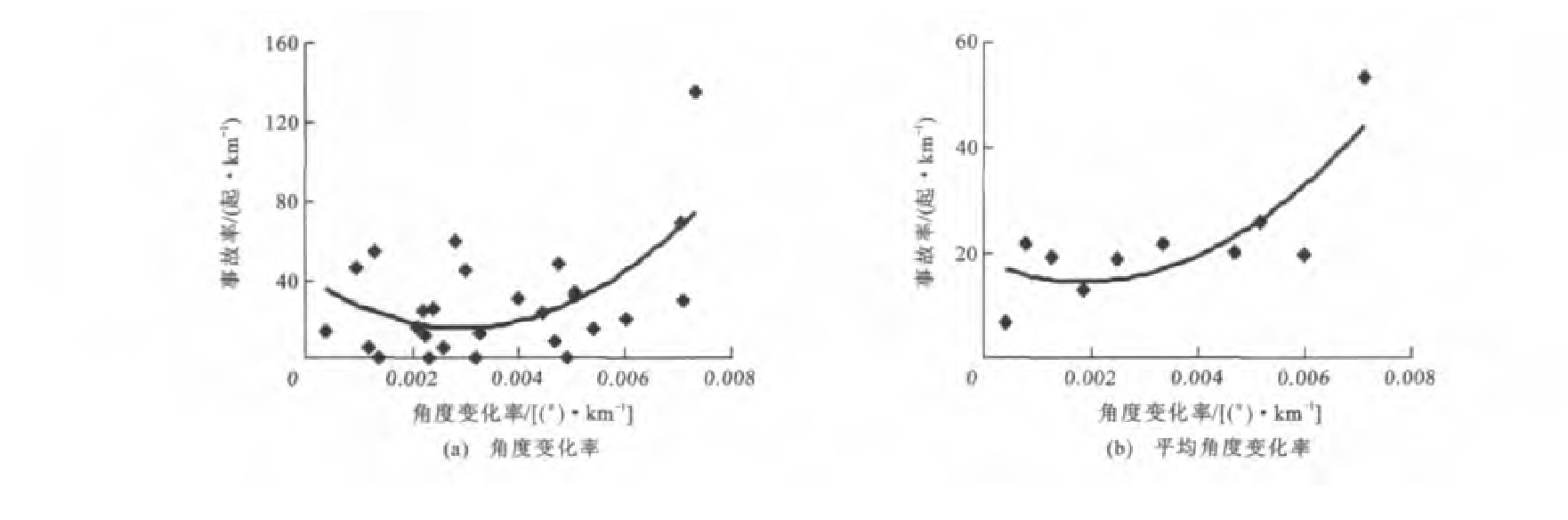
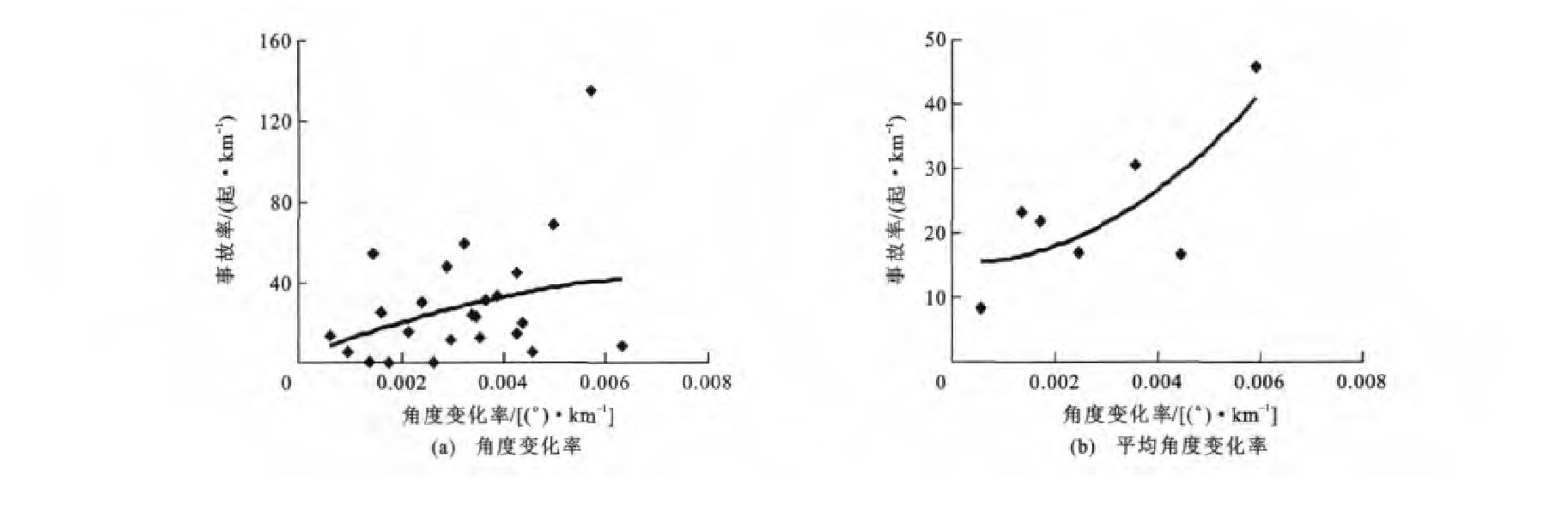
图 2 路段2事故率与角度变化率的关系Figure 2. Relation between and accident rate curvature change rate of section 2根据表 3中5个计算区间上的事故数量和对应的角度变化率, 得到路段1上5个计算区间的事故率与角度变化率的散点关系, 分别见图 3(a)~7(a), 再进一步均值化处理后, 事故率与平均角度变化率的拟合曲线分别见图 3(b)~7(b)。根据表 4中的5个计算区间事故数量和对应的角度变化率, 得到路段2上事故率与角度变化率的散点关系, 分别见图 8(a)~12(a), 再进一步均值化处理后, 事故率与平均角度变化率的拟合曲线分别见图 8(b)~12(b)。
图 3 路段1中A计算区间上事故率与角度变化率的关系Figure 3. Relations between accident rates and curvature change rates of calculation interval A on section 1
图 4 路段1中B计算区间上事故率与角度变化率的关系Figure 4. Relations between accident rates and curvature change rates of calculation interval B on section 1
图 5 路段1中C计算区间上事故率与角度变化率的关系Figure 5. Relations between accident rates and curvature change rates of calculation interval C on section 1
图 6 路段1中D计算区间上事故率与角度变化率的关系Figure 6. Relations between accident rates and curvature change rates of calculation interval D on section 1
图 7 路段1中E计算区间上事故率与角度变化率的关系Figure 7. Relations between accident rates and curvature change rates of calculation interval E on section 1
图 8 路段2中A计算区间上事故率与角度变化率的关系Figure 8. Relations between accident rates and curvature change rates of calculation interval A on section 2
图 9 路段2中B计算区间上事故率与角度变化率的关系Figure 9. Relations between accident rates and curvature change rates of calculation interval B on section 2
图 10 路段2中C计算区间上事故率与角度变化率的关系Figure 10. Relations between accident rates and curvature change rates of calculation interval C on section 2
图 11 路段2中D计算区间上事故率与角度变化率的关系Figure 11. Relations between accident rates and curvature change rates of calculation interval D on section 2
图 12 路段2中E计算区间上事故率与角度变化率的关系Figure 12. Relations between accident rates and curvature change rates of calculation interval E on section 2运用式(2)、(3)分别计算图 3~12回归方程, 并得到相应的拟合判定系数, 路段1、2拟合结果分别见表 5、6。由图 1、2可知, 路段1、2区间内的拟合结果分别为
对应的判定系数分别为0.414 2与0.120 8, y1、R1与y2、R2分别为路段1与路段2的事故率与角度变化率。
由图 1、3~7可知, 路段1四个计算区间的事故率与角度变化率之间呈现正的二次多项式关系, 但在E计算区间上, 事故率与平均角度变化率之间不呈现该分布规律。在B计算区间上, 该规律最为显著, 以0.001 0(°)·km-1为单位对角度变化率进行重新划分, 对每个区间的样本求平均值得到新样本, 当平均角度变化率为0.002 2(°)·km-1时, 事故率最低。在表 5中, 判定系数也表明当在B计算区间上时, 拟合精度最高, 达到了0.966 1;带下标的y、R、R分别为路段1上相应区间A~E上的事故率、角度变化率与平均角度变化率。
表 5 路段1拟合结果Table 5. Fitting result of section 1
由图 2、8~12可以看出, 路段2四个计算区间上的事故率与角度变化率之间也呈现正的二次抛物线关系, 但在E计算区间上, 事故率与平均角度变化率之间不呈现该分布规律。在B计算区间上, 该规律最显著, 以0.001 0(°)·km-1为单位对角度变化率进行重新划分, 对每个区间的样本求平均值得到新样本, 当平均角度变化率为0.001 8(°)·km-1时, 事故率最低。在表 6中, 判定系数也表明在B计算区间上, 拟合精度最高, 达到了0.790 8;带下标的y、R、R分别为路段2上相应区间A~E上的事故率、角度变化率与平均角度变化率。
表 6 路段2拟合结果Table 6. Fitting result of section 2
由此可见, 路段1、2基本呈现了相同的规律性, 即在B计算区间上, 事故率与平均角度变化率呈现的正二次抛物线关系最为强烈, 当平均角度变化率大约为0.002 0(°)·km-1时, 事故率最低。
3. 结语
(1) 本文选取的2个研究路段均为山区二级公路, 设计行车速度为40km·h-1, 弯道密度较大, 不包含长直线路段。如果研究对象的道路技术等级与设计车速高, 且平面线形更为平缓, 则本文的研究结论可能不适用。
(2) 由于样本量的原因, 本文得到的具体量化值, 适用范围和普遍性受到一定限制, 但用角度变化率表征平面线形特征, 研究平面线形和事故的关系, 反映的曲线特征具整体性。
(3) 在单一曲线内的事故发生不仅受该平面线形的影响, 而且还受到相邻路段线形, 特别是事故发生之前路段线形的影响。
-
图 1 路段1事故率与角度变化率的关系
Figure 1. Relation between accident rate and curvature change rate of section 1
图 2 路段2事故率与角度变化率的关系
Figure 2. Relation between and accident rate curvature change rate of section 2
图 3 路段1中A计算区间上事故率与角度变化率的关系
Figure 3. Relations between accident rates and curvature change rates of calculation interval A on section 1
图 4 路段1中B计算区间上事故率与角度变化率的关系
Figure 4. Relations between accident rates and curvature change rates of calculation interval B on section 1
图 5 路段1中C计算区间上事故率与角度变化率的关系
Figure 5. Relations between accident rates and curvature change rates of calculation interval C on section 1
图 6 路段1中D计算区间上事故率与角度变化率的关系
Figure 6. Relations between accident rates and curvature change rates of calculation interval D on section 1
图 7 路段1中E计算区间上事故率与角度变化率的关系
Figure 7. Relations between accident rates and curvature change rates of calculation interval E on section 1
图 8 路段2中A计算区间上事故率与角度变化率的关系
Figure 8. Relations between accident rates and curvature change rates of calculation interval A on section 2
图 9 路段2中B计算区间上事故率与角度变化率的关系
Figure 9. Relations between accident rates and curvature change rates of calculation interval B on section 2
图 10 路段2中C计算区间上事故率与角度变化率的关系
Figure 10. Relations between accident rates and curvature change rates of calculation interval C on section 2
图 11 路段2中D计算区间上事故率与角度变化率的关系
Figure 11. Relations between accident rates and curvature change rates of calculation interval D on section 2
图 12 路段2中E计算区间上事故率与角度变化率的关系
Figure 12. Relations between accident rates and curvature change rates of calculation interval E on section 2
表 1 路段1平面线形参数与事故分布
Table 1. Horizontal alignment parameters and accident distribution of section 1
下载: 导出CSV
表 2 路段2平面线形参数与事故分布
Table 2. Horizontal alignment parameters and accident distribution of section 2
下载: 导出CSV
-
[1] 杨宏志, 叶亚丽, 许金良, 等. 高速公路单车事故建模方法[J]. 交通运输工程学报, 2011, 11(1): 89-94. doi: 10.3969/j.issn.1671-1637.2011.01.015YANG Hong-zhi, YE Ya-li, XU Jin-liang, et al. Single-vehilce accident modeling method on freeway[J]. Journal of Traffic and Transportation Engineering, 2011, 11(1): 89-94. (in Chinese). doi: 10.3969/j.issn.1671-1637.2011.01.015 [2] 陈斌, 袁伟, 付锐, 等. 连续长大下坡路段交通事故特征分析[J]. 交通运输工程学报, 2009, 9(4): 75-78. doi: 10.3321/j.issn:1671-1637.2009.04.015CHEN Bin, YUAN Wei, FU Rui, et al. Analysis of traffic acci-dent characteristic on continuous long downgrade section[J]. Journal of Traffic and Transportation Engineering, 2009, 9(4): 75-78. (in Chinese). doi: 10.3321/j.issn:1671-1637.2009.04.015 [3] 崔洪军, 魏连雨, 朱敏清, 等. 公路平面设计中有关问题的探讨[J]. 中国公路学报, 2002, 15(1): 22-25. doi: 10.3321/j.issn:1001-7372.2002.01.006CUI Hong-jun, WEI Lian-yu, ZHU Min-qing, et al. Study of some horizontal curve design problems[J]. China Journal of Highway and Transport, 2002, 15(1): 22-25. (in Chinese). doi: 10.3321/j.issn:1001-7372.2002.01.006 [4] FU Rui, GUO Ying-shi, YUAN Wei, et al. The correlation between gradients of descending roads and accident rates[J]. Safety Science, 2011, 49(3): 416-423. doi: 10.1016/j.ssci.2010.10.006 [5] 孟祥海, 关志强, 郑来. 基于几何线形指标的山区高速公路安全性评价[J]. 中国公路学报, 2011, 24(2): 103-108. doi: 10.3969/j.issn.1001-7372.2011.02.017MENG Xiang-hai, GUAN Zhi-qiang, ZHENG Lai. Safety evaluation of mountainous expressway based on geometric alignment indexes[J]. China Journal of Highway and Transport, 2011, 24(2): 103-108. (in Chinese). doi: 10.3969/j.issn.1001-7372.2011.02.017 [6] 符锌砂, 龙昱. 公路线形安全性模糊综合评价[J]. 公路, 2008(6): 88-92. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200806023.htmFU Xin-sha, LONG Yu. Fuzzy synthetic evaluation of high-way alignment safety[J]. Highway, 2008(6): 88-92. (inChinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200806023.htm [7] 程文, 郭忠印, 孔令旗. 路线线形与道路安全关系的研究[J]. 合肥工业大学学报: 自然科学版, 2002, 25(5): 703-706. doi: 10.3969/j.issn.1003-5060.2002.05.014CHENG Wen, GUO Zhong-yin, Kong Ling-qi. Research on the relation between road line features and road safety[J]. Journal of Hefei University of Technology: Natural Science, 2002, 25(5): 703-706. (in Chinese). doi: 10.3969/j.issn.1003-5060.2002.05.014 [8] 郭凤香. 道路线形安全分析与评价[D]. 昆明: 昆明理工大学, 2005.GUO Feng-xiang. Safety analysis and evaluation of road alignment[D]. Kunming: Kunming University of Science and Technology, 2005. (in Chinese). [9] 王华荣, 孙小端, 贺玉龙, 等. 山区双车道公路尾随相撞事故与道路线形的关系[J]. 北京工业大学学报, 2010, 36(9): 1236-1241. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201009014.htmWANG Hua-rong, SUN Xiao-duan, HE Yu-long, et al. Effects of geometric features of rear-end crash accidents on moutainous two-lane highways[J]. Journal of Beijing University of Technology, 2010, 36(9): 1236-1241. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201009014.htm [10] 陈永胜, 高耀华. 高速公路纵面设计微观事故预测模型研究[J]. 公路交通科技, 2001, 18(2): 5-8. doi: 10.3969/j.issn.1002-0268.2001.02.002CHEN Yong-sheng, GAO Yao-hua. Study on microcosmic accident-predict model focused on vertical design of express-way[J]. Journal of Highway and Transportation Research and Development, 2001, 18(2): 5-8. (in Chinese). doi: 10.3969/j.issn.1002-0268.2001.02.002 [11] 邹健. 浅谈道路线形设计对交通安全的影响及改善措施[J]. 公路, 2002(6): 42-47. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200206015.htmZOU Jian. Research on effect and improvement measures of road alignment design on road traffic safety[J]. Highway, 2002(6): 42-47. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200206015.htm [12] VOGT A, BARED J G. Accident models for two-lane rural roads: segments and intersections[R]. Mclean: Federal Highway Administration, 1998. [13] GLENNON J C, NEUMAN T R, LEISCH J E, et al. Safety and operational considerations for design of rural highway curves[R]. Mclean: Federal Highway Administration, 1985. [14] 景天然. 交通事故与公路条件的关系[J]. 同济大学学报: 自然科学版, 1991, 19(3): 287-294. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ199103004.htmJING Tian-ran. Relation between traffic and highway and highway conditions[J]. Journal of Tongji University: Nat-ural Science, 1991, 19(3): 287-294. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ199103004.htm [15] 黄进, 方守恩. 平曲线路段事故数目与线形元素的关系[J]. 公路, 2002(12): 76-79. doi: 10.3969/j.issn.0451-0712.2002.12.019HUANG Jin, FANG Shou-en. Relationship between accident number and alignment elements of horizontal curve sections[J]. Highway, 2002(12): 76-79. (in Chinese). doi: 10.3969/j.issn.0451-0712.2002.12.019 [16] KARLAFTIS M G, GOLIAS I. Effects of road geometry and traffic volumes on rural roadway accident rates[J]. Accidents Analysis and Prevention, 2002, 34(3): 357-365. doi: 10.1016/S0001-4575(01)00033-1 [17] 杨宏志, 胡庆谊, 许金良. 高速公路长大下坡路段安全设计与评价方法[J]. 交通运输工程学报, 2010, 10(3): 10-16. doi: 10.3969/j.issn.1671-1637.2010.03.002YANG Hong-zhi, HU Qing-yi, XU Jin-liang. Safety design and evaluation method of long-steep downgrade sections for expressway[J]. Journal of Traffic and Transportation Engineering, 2010, 10(3): 10-16. (in Chinese). doi: 10.3969/j.issn.1671-1637.2010.03.002 [18] FITZPATRICK K, ELEFTERIADOU L, HARWOO D W, et al. Speed prediction for two-lane rural highways[R]. Mclean: Federal Highway Administration, 2000. [19] WAING J C. Quantifying the relationship between geometric design consistency and road safety[D]. Vancouver: The University of British Columbia, 2002. [20] 杜水友, 章皓, 郑永军, 等. 最小二乘法拟合压力传感器二次曲线及精度分析[J]. 中国计量学院学报, 2005, 16(3): 185-187. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJL200503003.htmDU Shui-you, ZHANG Hao, ZHENG Yong-jun, et al. The secondary order curve of pressure sensors decided by the least square and accuracy analysis[J]. Journal of China Jiliang University, 2005, 16(3): 185-187. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJL200503003.htm [21] 林雨, 杨轸, 潘晓东. 缓和曲线长度对车辆行驶轨迹的影响[J]. 西南交通大学学报, 2011, 46(2): 200-204. doi: 10.3969/j.issn.0258-2724.2011.02.004LIN Yu, YANG Zhen, PAN Xiao-dong. Effect of spiral transition curve length on vehicle path[J]. Journal of Southwest Jiao-tong University, 2011, 46(2): 200-204. (in Chinese). doi: 10.3969/j.issn.0258-2724.2011.02.004 [22] 章锡俏, 李松龄, 杨龙海. 寒冷地区设超高公路圆曲线半径设计仿真研究[J]. 武汉理工大学学报, 2011, 33(6): 64-67. https://www.cnki.com.cn/Article/CJFDTOTAL-WHGY201106016.htmZHANG Xi-qiao, LI Song-ling, YANG Long-hai. Simulation analysis of superelevation highway circular curve radius design in cold regions[J]. Journal of Wuhan University of Technology, 2011, 33(6): 64-67. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-WHGY201106016.htm [23] 潘晓东, 方青, 蒋宏. 基于驾驶视觉需求的山区公路平曲线安全评价[J]. 同济大学学报: 自然科学版, 2010, 38(12): 1763-1766. doi: 10.3969/j.issn.0253-374x.2010.12.009PAN Xiao-dong, FANG Qing, JIANG Hong. Driving visual demand-based safety evaluation of mountainous highway horizontal curve[J]. Journal of Tongji University: Natural Science, 2010, 38(12): 1763-1766. (in Chinese). doi: 10.3969/j.issn.0253-374x.2010.12.009 -
下载:
点击查看大图
计量
- 文章访问数: 938
- HTML全文浏览量: 182
- PDF下载量: 735
- 被引次数: 0
