基于压缩传感的交通流量数据压缩方法

李清泉; 周尧; 乐阳; 叶嘉安

doi:10.19818/j.cnki.1671-1637.2012.03.017

基于压缩传感的交通流量数据压缩方法

doi: 10.19818/j.cnki.1671-1637.2012.03.017

李清泉^{1, 2,},
周尧^{2, 3},
乐阳^{1, 2},
叶嘉安⁴

1.
武汉大学测绘遥感信息工程国家重点实验室, 湖北武汉 430079
2.
武汉大学时空数据智能获取技术与应用教育部工程研究中心, 湖北武汉 430079
3.
武汉大学测绘学院, 湖北武汉 430079
4.
香港大学城市研究及城市规划中心, 香港

基金项目:

国家自然科学基金项目 41171348

国家自然科学基金项目 60872132

国家自然科学基金项目 40830530

香港研究资助局项目 HKU754109

详细信息

作者简介:
李清泉(1965-), 男, 安徽天长人, 武汉大学教授, 工学博士, 从事地理信息系统与智能交通研究

中图分类号: U491.112
计量
- 文章访问数: 869
- HTML全文浏览量: 118
- PDF下载量: 1183
- 被引次数: 0
出版历程
- 收稿日期: 2012-01-17
- 刊出日期: 2012-06-25

Compression method of traffic flow data based on compressed sensing

LI Qing-quan^{1, 2
,},
ZHOU Yao^{2, 3},
LE Yang^{1, 2},
YE Jia-an⁴

1.
State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, Hubei, China
2.
Engineering Research Center for Spatio-Temporal Data Smart Acquisition and Application of Ministry of Education, Wuhan University, Wuhan 430079, Hubei, China
3.
School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, Hubei, China
4.
Centre of Urban Studies and Urban Planning, The University of Hong Kong, Hong Kong, China

More Information

Author Bio:
LI Qing-quan (1965-), male, professor, PhD, +86-27-68778222, qqli@whu.edu.cn

Article Text (Baidu Translation)

摘要

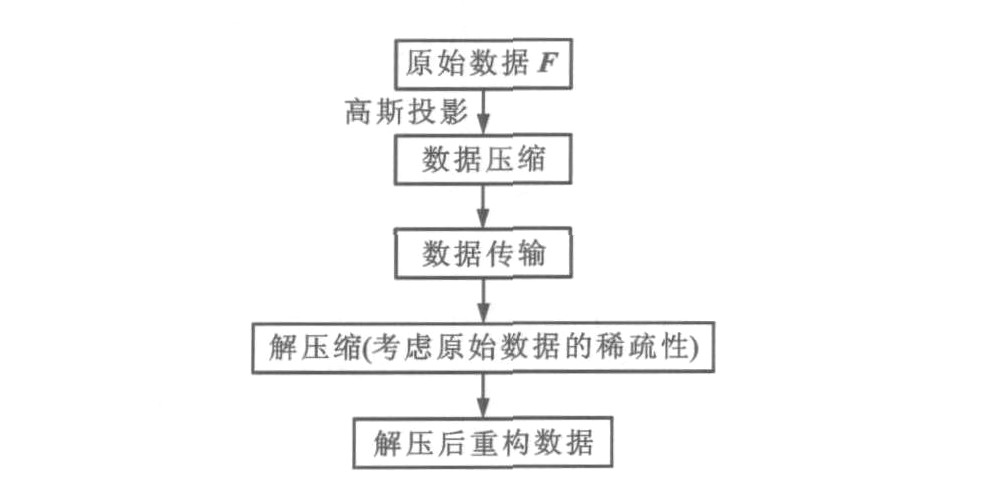
摘要: 为准确获得用于数据压缩的变换矩阵, 引入了基于压缩传感的交通流量数据压缩方法, 在数据压缩端无需考虑变换矩阵的选择问题, 直接通过高斯投影实现高效数据压缩。首先验证了交通流量数据在经过K-SVD方法训练过的字典上能够实现稀疏表达; 然后在数据压缩端, 通过具有限制性等距条件的随机矩阵将原始高维数据投影到低维空间上, 实现数据的高效快速压缩; 最后在数据传输后, 通过凸优化算法在交通信息处理端完成数据解压缩。以美国某高速公路线圈传感器采集到的交通流量数据, 对本文方法进行了验证。试验证明: 该方法能够实现快速高效的压缩编码, 当压缩比为4∶1时, 解压缩相对误差仅为0.060 8。
- 智能交通系统 /
- 压缩传感 /
- 数据压缩 /
- 冗余字典 /
- 高斯投影 /
- L1-合成算法
Abstract: In order to obtain transformation matrix accurately, a new compression method of traffic flow data based on compressed sensing was introduced.The original data were projected into the low-dimension space directly by Gauss projection regardless of transformation matrix selection at the data compression side.Firstly, traffic flow data were proved to have sparse representation under the K-SVD trained dictionary.Secondly, original high-dimension data were projected into low-dimension space at the data compression side by using the random matrix with restricted isometry property, which made efficient and rapid data compression possible.Finally, after data transmission, data decompression were accomplished by convex algorithm at the data processing side.The traffic flow data obtained from the coil sensors located on a certain highway of America were used to validated the new method.The experimental result shows that the data compression method is fast and efficient.When the compression ratio is 4∶1, the relative error of data decompression is only 0.060 8.
- intelligent transportation system /
- compressed sensing /
- data compression /
- redundant dictionary /
- Gauss projection /
- L1-synthesis algorithm

HTML全文

图 1 压缩传感流程

Figure 1. Compressed sensing flow

下载: 全尺寸图片幻灯片

图 2 传统数据压缩流程

Figure 2. Traditional data compression flow

下载: 全尺寸图片幻灯片

图 3 压缩流程

Figure 3. Compression flow

下载: 全尺寸图片幻灯片

图 4 不同域的压缩传感数据

Figure 4. Compressed sensing data in different domains

下载: 全尺寸图片幻灯片

图 5 线圈传感器分布

Figure 5. Distribution of coil sensors

下载: 全尺寸图片幻灯片

图 6 车道与线圈传感器的关系

Figure 6. Relationship between coil sensors and lanes

下载: 全尺寸图片幻灯片

图 7 F与f的比较

Figure 7. Comparison of F and f

下载: 全尺寸图片幻灯片

图 8 F与F′的比较

Figure 8. Comparison of F and F′

下载: 全尺寸图片幻灯片

表 1 检测站地理位置

Table 1. Geographical locations of inspection stations

检测站	经度/(°)	纬度/(°)	所属高速路	方向
1	93.40	45.08	I-94	北
2	93.31	45.07	I-94	北

下载: 导出CSV

表 2 线圈传感器的检测值

Table 2. Detection values of coil sensors

时间段	车流量/(veh·h^-1)	占有率/%
1	2 760	10
2	1 680	7
3	1 920	6
4	2 400	10
5	2 520	6
6	1 320	7
7	1 440	7
8	2 880	11
9	2 160	6
10	1 440	8
11	2 040	7
12	2 040	6
13	2 280	10
14	2 280	4
15	960	8
16	2 160	8
17	1 440	10
18	3 480	10
19	2 640	13
20	2 400	7

下载: 导出CSV

表 3 稀疏表达误差分析

Table 3. Error analysis of sparse representation

原始数长度	字典原子个数	稀疏表达选用原子个数	相对误差‖F-f‖₂/‖F‖₂
120	2 000	10	0.033 2

下载: 导出CSV

表 4 压缩传感误差分析

Table 4. Error analysis of compressed sensing

原始数据长度	压缩后数据长度	压缩比	相对误差‖F-F′‖₂/‖F‖₂
120	30	4∶1	0.060 8

下载: 导出CSV

表 5 数据压缩端对比

Table 5. Comparison at data compression side

	乘法次数	加法次数	计算量
正交变换	N²	N(N-1)	O(N²)
压缩传感	MN	M(N-1)	O(MN)

下载: 导出CSV

参考文献(18)

[1]	肖扬, 鲁凌云, 高爽, 等. 基于二维离散小波变换的智能交通系统数据去噪声压缩[J]. 北京交通大学学报, 2004, 28(5): 1-5. doi: 10.3969/j.issn.1673-0291.2004.05.001 XIAO Yang, LU Ling-yun, GAO Shuang, et al. Traffic data denoising compression for intelligent traffic systems based on2-D discrete wavelet transformation[J]. Journal of Beijing Jiaotong University, 2004, 28(5): 1-5. (in Chinese). doi: 10.3969/j.issn.1673-0291.2004.05.001
[2]	练秋生, 王成儒, 孔令富. 心电图压缩算法中的小波基选择[J]. 计算机工程与应用, 2002, 38(18): 6-8. doi: 10.3321/j.issn:1002-8331.2002.18.003 LIAN Qiu-sheng, WANG Cheng-ru, KONG Ling-fu. The choice of wavelet in electrocardiogram compression algorithm[J]. Computer Engineering and Applications, 2002, 38(18): 6-8. (in Chinese). doi: 10.3321/j.issn:1002-8331.2002.18.003
[3]	COIFMAN R R, WICKERHAUSER M V. Entropy-based algorithms for best basis selection[J]. IEEE Transactions on Information Theory, 1992, 38(2): 713-718. doi: 10.1109/18.119732
[4]	蔡敦虎. 多种小波基的图像去噪性能研究[D]. 武汉: 武汉大学, 2003. CAI Dun-hu. The research on the performance of manifold wavelet basis in image denoising[D]. Wuhan: Wuahan University, 2003. (in Chinese).
[5]	费铭薇, 乐全明, 张沛超, 等. 电力系统故障录波数据压缩与重构小波基选择[J]. 电力系统自动化, 2005, 29(17): 64-67, 97. doi: 10.3321/j.issn:1000-1026.2005.17.012 FEI Ming-wei, YUE Quan-ming, ZHANG Pei-chao, et al. Wavelets selection of compression and reconstruction algorithm based on digital recorded data from a faulted power system[J]. Automation of Electric Power Systems, 2005, 29(17): 64-67, 97. (in Chinese). doi: 10.3321/j.issn:1000-1026.2005.17.012
[6]	魏玉芬, 梦艳君. 图像编码压缩小波基的选择[J]. 装备制造技术, 2009(4): 49-50, 61. doi: 10.3969/j.issn.1672-545X.2009.04.020 WEI Yu-fen, MENG Yan-jun. The choice of orthogonal wavelets base in image compression[J]. Equipment Manufac-turing Technology, 2009(4): 49-50, 61. (in Chinese). doi: 10.3969/j.issn.1672-545X.2009.04.020
[7]	赵志强, 张毅, 胡坚明, 等. 基于PCA和ICA的交通流量数据压缩方法比较研究[J]. 公路交通科技, 2008, 25(11): 109-118. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200811022.htm ZHAO Zhi-qiang, ZHANG Yi, HU Jian-ming, et al. Compara-tive study of PCA and ICA based traffic flow compression[J]. Journal of Highway and Transportation Research and Devel-opment, 2008, 25(11): 109-118. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200811022.htm
[8]	QU Li, HU Jian-ming, ZHANG Yi. A flow volumes data compression approach for traffic network based on principal component analysis[C]∥IEEE. Proceedings of the2007IEEE Intelligent Transportation Systems Conference. Seattle: IEEE, 2007: 125-130.
[9]	耿彦斌, 于雷, 武旭, 等. 基于信号处理技术的ITS数据压缩方法与应用[J]. 土木工程学报, 2006, 39(11): 107-113. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200611017.htm GENG Yan-bin, YU Lei, WU Xu, et al. Signal-processing-based ITS data compression techniques and applications[J]. China Civil Engineering Journal, 2006, 39(11): 107-113. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200611017.htm
[10]	CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083
[11]	DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582
[12]	CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. doi: 10.1109/MSP.2007.914731
[13]	金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2): 470-475. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201002041.htm JIN Jian, GU Yuan-tao, MEI Shun-liang. An introduction to compressive sampling and its applications[J]. Journal of Electronics and Information Technology, 2010, 32(2): 470-475. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DZYX201002041.htm
[14]	RAUHUT H, SCHNASS K, VAN DERGHEYNST P. Compressed sensing and redundant dictionaries[J]. IEEE Transactions on Information Theory, 2008, 54(5): 2210-2219. https://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=4494699&contentType=Journals+%26+Magazines
[15]	CANDES E J, ELDAR Y C, NEEDELL D, et al. Com-pressed sensing with coherent and redundant dictionaries[J]. Applied and Computational Harmonic Analysis, 2011, 31(1): 59-73. https://www.sciencedirect.com/science/article/pii/S1063520310001156
[16]	AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. https://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.89.4935&rank=5&q=sparse%20radon%20transform&osm=&ossid=
[17]	徐鹏. 信号的稀疏分解及其在脑电信号处理中的应用研究[D]. 成都: 电子科技大学, 2006. XU Peng. Study on sparse decomposition of signal and its application in EEG processing[D]. Chengdu: University of Electronic Science and Technology of China, 2006. (in Chinese).
[18]	TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. https://authors.library.caltech.edu/27144