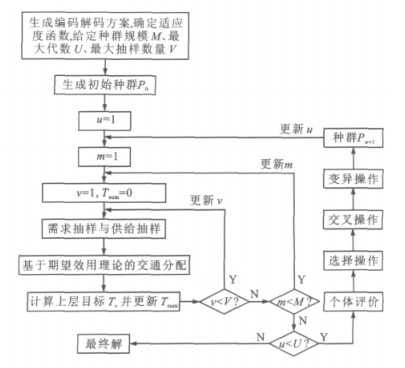
Design model of traffic network based on stochastic supply and stochastic demand
Article Text (Baidu Translation)
-
摘要: 为了改进以确定供给与确定需求为基础的传统交通网络设计方案, 根据双层规划理论与交通分配理论, 建立了基于随机供给与随机需求的离散交通网络设计模型。将Monte Carlo模拟、遗传算法和交通分配算法应用于模型求解过程, 并应用Nguyen-Dupuis交通网络求解模型。计算结果表明: 当OD需求增大时, 总走行时间增大; 当建设预算增大时, 总走行时间下降; 当供给与需求均不确定时, 增加建设预算对降低总走行时间的效果更加明显; 在不同工况下, 总走行时间最大值为1.69×105 h, 最小值为8.89×104 h; 当OD需求均值为350 veh.h-1, 建设预算从1 000万元增大到1 500万元, 且供给确定时, 总走行时间下降3.47%。供给与需求的不确定程度对交通网络的设计方案具有重要影响。Abstract: In order to improve the traditional design method of traffic network based on definitive supply and definitive demand, the hi-level programming theory and traffic assignment theory were used, and the design model of traffic network based on stochastic supply and stochastic demand was set up. The Monte Carlo simulation, genetic algorithm and traffic assignment algorithm were applied in model solving process, and Nguyen-Dupuis traffic network was used to solve the model. Calculation result indicates that when the OD demand increases, the total travel time increases. When the construction budget increases, the total travel time decreases. When both supply and demand are uncertain, the effect of increasing construction budget on decreasing total travel time is more significant. Under different conditions, the maximum value of total travel time is 1.69 ×105 h, and the minimum value is 8.89 ×104 h. When the average value of OD demand is 350 veh·h-1 and the construction budget increases from 10 million yuan to 15 million yuan, the total travel time decreases by 3.47% under certain supply. The uncertain degrees of stochastic supply and stochastic demand have important influence on the design method of trafficnetwork. 9 tabs, 17 figs, 19 refs.
-
表 1 OD需求数据
Table 1. OD demand data
OD对编号 起点编号 终点编号 OD需求均值/（veh·h-1） 1 1 2 350 2 1 3 350 3 4 2 350 4 4 3 350 
下载: 导出CSV
表 2 工况1~4的基本参数
Table 2. Basic parameters of conditions 1-4
工况 OD需求均值/（veh·h-1） 变异系数κ 现状参数θa0 规划参数θa 建设预算B/万元 抽样规模/个 1 350 0 1 1 1000 1 2 500 0 1 1 1000 1 3 350 0 1 1 1500 1 4 500 0 1 1 1500 1
下载: 导出CSV
表 3 工况1~4的计算结果
Table 3. Calculation results of conditions 1-4
工况 新建路段编号 扩建路段编号 最优目标函数值/104h 1 20，21，22，23，25 3，4，10，13，15 9.21 2 20，22，24 2，3，5，7，9，11，16 16.90 3 20，22，23，25 2，3，4，5，6，9，11，12，13，14，16 8.89 4 20，21，22，23，24，25 2，3，4，5，7，10，11，15，19 14.30
下载: 导出CSV
表 4 工况5~7的基本参数
Table 4. Basic parameters of conditions 5-7
工况 变异系数κ 现状参数θa0 规划参数θa 建设预算B/万元 抽样规模/个 5 0.1 1 1 1000 50 6 0.2 1 1 1000 50 7 0.5 1 1 1000 50
下载: 导出CSV
表 5 工况5~7计算结果
Table 5. Calculation results of conditions 5-7
工况 新建路段编号 扩建路段编号 最优目标函数值/104h 5 21，23，24 1，3，5，6，12，14，15 9.16 6 21，23，24，25 1，3，6，12，14，15 8.94 7 21，23 2，3，7，9，13，14，15，16 9.09
下载: 导出CSV
表 6 工况8~11的基本参数
Table 6. Basic parameters of conditions 8-11
工况 OD需求均值/（veh·h-1） 变异系数κ 现状参数θa0 规划参数θa 建设预算B/万元 抽样规模/个 8 350 0 0.9 0.9 1000 50 9 350 0 0.8 0.8 1000 50 10 350 0 0.9 0.9 1500 50 11 350 0 0.8 0.8 1500 50
下载: 导出CSV
表 7 工况8~11计算结果
Table 7. Calculation results of conditions 8-11
工况 新建路段编号 扩建路段编号 最优目标函数值/104h 8 20，21，22，23，24 2，3，7，15，19 9.39 9 20，21，22，23 3，4，11，14，15，16 9.66 10 20，21，22，23 1，3，4，5，6，7，11，13，14，15，16 8.98 11 21，22，23，25 1，2，3，4，5，11，12，13，14，15，16 9.11
下载: 导出CSV
表 8 工况12~15的基本参数
Table 8. Basic parameters of conditions 12-15
工况 OD需求均值/（veh·h-1） 变异系数κ 现状参数θa0 规划参数θa 建设预算B/万元 抽样规模/个 12 350 0.1 0.9 0.9 1000 50 13 350 0.1 0.8 0.8 1000 50 14 350 0.2 0.9 0.9 1000 50 15 350 0.2 0.8 0.8 1000 50
下载: 导出CSV
表 9 工况12~15计算结果
Table 9. Calculation results of conditions 12-15
工况 新建路段编号 扩建路段编号 最优目标函数值/104h 12 20，22，25 3，5，7，10，14，15，16 9.37 13 21，22，24 1，3，5，10，14，15，16 9.67 14 20，21，23 3，5，7，11，14，15，16 9.10 15 22，24，25 2，3，5，6，10，13，15 9.19
下载: 导出CSV
-
[1] YANG Hai, BELL M G H. Models and algorithms for road network design: a review and some new developments[J]. Transport Reviews, 1998, 18(3): 257-278. doi: 10.1080/01441649808717016 [2] WONG S C, YANG Hai. Reserve capacity for a signal controlled road network[J]. Transportation Research Part B: Methodological, 1997, 31(5): 397-402. doi: 10.1016/S0191-2615(97)00002-7 [3] 许良, 高自友. 基于连通可靠性的城市道路交通离散网络设计问题[J]. 燕山大学学报, 2007, 31(2): 159-163. doi: 10.3969/j.issn.1007-791X.2007.02.014XU Liang, GAO Zi-you. Urban road transportation discrete network design based on connectivity reliability[J]. Journal of Yanshan University, 2007, 31(2): 159-163. (in Chinese) doi: 10.3969/j.issn.1007-791X.2007.02.014 [4] 刘娟娟, 范炳全, 祝炳发. 双层规划在城市交通污染控制中的一个应用[J]. 管理工程学报, 2005, 19(4): 87-90. doi: 10.3969/j.issn.1004-6062.2005.04.018LIU Juan-juan, FAN Bing-quan, ZHU Bing-fa. An apply of bilevle programming in the urban transport pollution control[J]. Journal of Industrial Engineering and Engineering Management, 2005, 19(4): 87-90. (in Chinese) doi: 10.3969/j.issn.1004-6062.2005.04.018 [5] MENG Qiang, YANG Hai. Benefit distribution and equity in road network design[J]. Transportation Research Part B: Methodological, 2002, 36(1): 19-35. doi: 10.1016/S0191-2615(00)00036-9 [6] FRIESZ T L, ANANDALINGAM G, MEHTA N J, et al. The multiobjective equilibrium network design problem revisited: a simulated annealing approach[J]. European Journal of Operational Research, 1993, 65(1): 44-57. doi: 10.1016/0377-2217(93)90143-B [7] TZENG G H, TSAUR S H. Application of multiple criteria decision making for network improvement plan model[J]. Journal of Advanced Transportation, 1997, 31(1): 48-74. [8] UKKUSUI S V, MATHEW T V, WALLER S T. Robust transportation network design under demand uncertainty[J]. Computer-Aided Civil and Infrastructure Engineering, 2007, 22(1): 6-18. doi: 10.1111/j.1467-8667.2006.00465.x [9] YIN Ya-feng, MADANAT S M, LU Xiao-yun. Robust improvement schemes for road networks under demand uncertainty[J]. European Journal of Operational Research, 2009, 198(2): 470-479. doi: 10.1016/j.ejor.2008.09.008 [10] WATLING D. A second order stochastic network equilibrium model, Ⅰ: theoretical foundation[J]. Transportation Science, 2002, 36(2): 149-183. doi: 10.1287/trsc.36.2.149.560 [11] CLARK S, WATLING D. Modeling network travel time reliability under stochastic demand[J]. Transportation Research Part B: Methodological, 2005, 39(2): 119-140. doi: 10.1016/j.trb.2003.10.006 [12] SHAO Hu, LAM W H K, TAM M L. A reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand[J]. Networks and Spatial Economics, 2006, 6(3): 173-204. [13] KAROONSOONTAWONG A, WALLER S T. Integrated network capacity expansion and traffic signal optimization problem: robust bi-level dynamic formulation[J]. Network and Spatial Economics, 2009, 10(4): 525-550. [14] CHEN A, YANG Hai, LO H K, et al. A capacity related reliability for transportation network[J]. Journal of Advanced Transportation, 1999, 33(2): 183-200. doi: 10.1002/atr.5670330207 [15] LO H K, LUOX W, SIUBW Y. Degradable transport network: travel time budget of travellers with heterogeneous risk aversion[J]. Transportation Research Part B: Methodological, 2006, 40(9): 792-806. doi: 10.1016/j.trb.2005.10.003 [16] SIUB W Y, LO H K. Doubly uncertain transportation network: degradable capacity and stochastic demand[J]. European Journal of Operational Research, 2008, 191(1): 166-181. doi: 10.1016/j.ejor.2007.08.026 [17] LAM W H K, SHAO Hu, SUMALEE A. Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply[J]. Transportation Research Part B: Methodological, 2008, 42(10): 890-910. doi: 10.1016/j.trb.2008.02.004 [18] NGUYEN S, DUPUIS C. An efficient method for computing traffic equilibria in networks with asymmetric transportation costs[J]. Transportation Science, 1984, 18(2): 185-202. doi: 10.1287/trsc.18.2.185 [19] 陆化普, 蔚欣欣, 卞长志. 发生吸引量不确定的离散交通网络设计模型[J]. 统计与决策, 2011(6): 8-12. https://www.cnki.com.cn/Article/CJFDTOTAL-TJJC201106004.htmLU Hua-pu, YU Xin-xin, BIAN Chang-zhi. Model and algorithm of discrete network design problem under trip production-attraction uncertainty[J]. Statistics and Decision, 2011(6): 8-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJJC201106004.htm -
点击查看大图
图(17) / 表(9)
计量
- 文章访问数: 1065
- HTML全文浏览量: 153
- PDF下载量: 1248
- 被引次数: 0
