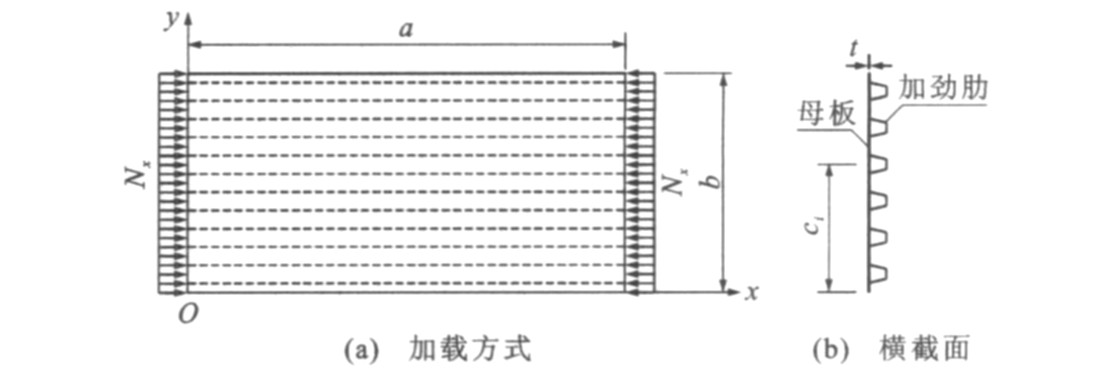
Calculation method of critical buckling stress for stiffened plate with closed ribs
-
摘要: 采用能量法, 推导了单向均匀受压四边简支闭口肋加劲板屈曲临界应力计算方法, 考虑加劲肋扭转刚度的影响, 按照截面实际形心位置计算了加劲肋和母板的抗弯刚度。以苏通大桥钢箱梁中采用的梯形闭口肋加劲板为例, 采用Timoshenko方法、小西一郎方法、板壳有限元法及提出的能量法进行了屈曲临界应力比较。分析结果表明: 加劲板长宽比β小于1时, Timoshenko方法和小西一郎方法计算的临界应力与钢材屈服强度比值λ大于能量法计算值; β在1~6之间时, Timoshenko方法和小西一郎方法计算的λ值小于能量法计算值; β在3~6之间时, 能量法计算值与有限元分析结果最接近, 偏差在9%~25%之间。可见, 采用能量法进行正交异性钢箱梁顶、底板弹性稳定分析可行。Abstract: A calculation method of critical buckling stress for stiffened plate with closed ribs was proposed by using energy method under unidirectional uniform pressure and simply supported on four sides. The influence of torsional rigidity of stiffened ribs was considered, the whole flexural rigidity of mother board and stiffened ribs was calculated according to the centroid of actual section. The stiffened plates with closed trapezoidal ribs in the steel box girder of Suzhou-Nantong Bridge were taken as example, the critical buckling stresses calculated by Timoshenko method, Ichiro Konishi method, shell finite element method and the proposed energy method were compared. Analysis result shows that when the length-width ratio β of stiffened plate is less than 1, the ratio λ values of critical buckling stress to steel yield strength calculated by Timoshenko method and Ichiro Konishi method are greater than the calculation value of energy method. When β is between 1 to 6, the λ values calculated by Timoshenko method and Ichiro Konishi method are less than the calculation value of energy method. When β is between 3 to 6, the calculation value of energy method is most approaching with the result of finite element analysis, their difference is between 9% to 25%. So the proposed energy method is feasible to analyze the elastic stabilities of top and bottom plates for orthotropic steel box girder.
-
表 1 加劲板参数
Table 1. Parameters of stiffened plates mm
加劲板号 参数 B t bf bs h tw tf R1 R2 SP1 800 24 404 254 262 8 8 34 34 SP2 800 20 404 254 262 8 8 34 34 SP3 800 18 404 254 262 8 8 34 34 SP4 800 16 404 254 262 8 8 34 34 表 2 三种方法计算的λ值与有限元法计算值的偏差比例
Table 2. Difference ratios ofλvalues calculated by three methods to values calculated by finite element method %
加劲板号 计算方法 β 1 2 3 4 5 6 SP1 Timoshenk 33 -39 -65 -72 -68 -62 小西一郎 48 -33 -62 -70 -67 -61 本文 52 34 17 10 19 25 SP2 Timoshenk 50 -36 -66 -76 -76 -73 小西一郎 65 -30 -64 -74 -75 -72 本文 64 37 19 9 14 18 SP3 Timoshenk 62 -33 -66 -77 -78 -77 小西一郎 76 -28 -63 -76 -77 -76 本文 71 40 21 10 14 16 SP4 Timoshenk 61 -30 -65 -78 -80 -80 小西一郎 73 -24 -63 -76 -79 -80 本文 65 44 24 11 15 16 -
[1] 李立峰, 邵旭东. 正交异性闭口加劲板的承载力分析理论及试验研究[J]. 土木工程学报, 2007, 40(6): 42-48. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200706008.htmLI Li-feng, SHAO Xu-dong. Theoretical study and model test on the capacity of orthotropic U-rib stiffened plates[J]. China Civil Engineering Journal, 2007, 40(6): 42-48. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200706008.htm [2] 李立峰, 邵旭东, 易伟建, 等. 扁平钢箱梁局部稳定模型试验[J]. 中国公路学报, 2007, 20(3): 60-65. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200703010.htmLI Li-feng, SHAO Xu-dong, YI Wei-jian, et al. Model test on local stability of flat steel box girder[J]. China Journal of Highway and Transport, 2007, 20(3): 60-65. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200703010.htm [3] 程斌, 肖汝诚, 赵金城. 双轴受压小刚度加劲厚板的极限强度计算[J]. 土木工程学报, 2010, 43(6): 87-93. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201006012.htmCHENG Bin, XIAO Ru-cheng, ZHAO Jin-cheng. Calcula-tion of ultimate strength for slightly stiffened thick panels under biaxial compression[J]. China Civil Engineering Journal, 2010, 43(6): 87-93. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201006012.htm [4] 狄谨, 周绪红, 吕忠达, 等. 正交异性钢箱梁U型肋加劲板极限承载力试验[J]. 中国公路学报, 2009, 22(2): 59-64. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200902010.htmDI Jin, ZHOU Xu-hong, LU Zhong-da, et al. Experiment on ultimate bearing capacity of U-stiffened plate of orthotropic steel box girder[J]. China Journal of Highway and Trans-port, 2009, 22(2): 59-64. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200902010.htm [5] 胡毓仁, 陈伯真, 孙久龙. 纵向受压板架加强筋扭转屈曲临界应力公式[J]. 上海交通大学学报, 2002, 36(1): 95-98. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT200201025.htmHU Yu-ren, CHEN Bo-zhen, SUN Jiu-long. Equation for predicting tripping stress of stiffeners in stiffened panels[J]. Journal of Shanghai Jiaotong University, 2002, 36(1): 95-98. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT200201025.htm [6] 王志伟. 按无量纲屈服准则分析正交异性板的极限荷载[J]. 哈尔滨工业大学学报, 2002, 34(2): 282-284. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX200202035.htmWANG Zhi-wei. Orthotopic board analysis of limit loads by dimensionless stress yield criterion[J]. Journal of Harbin Institute of Technology, 2002, 34(2): 282-284. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX200202035.htm [7] GRONDIN G Y, ELWI A E, CHENG J J R. Buckling of stiffened steel plates—aparametric study[J]. Journal of Con-structional Steel Research, 1999, 50(2): 151-175. [8] BEDAIR O K. Stability, free vibration, and bending behav-ior of multistiffened plates[J]. Journal of Engineering Mechanics, 1997, 123(4): 328-337. [9] BUTLER R, LILLICO M, HUNT G W, et al. Experiments on interactive buckling in optimized stiffened panels[J]. Structural and Multidisciplinary Optimization, 2001, 23(1): 40-48. [10] GREGOR P, WOLLMANN P E. Steel girder design per AASHTO LRFD specifications(Part2)[J]. Journal of Bridge Engineering, 2004, 9(4): 375-381. [11] GHAVAMI K, KHEDMATI M R. Numerical and experi-mental investigations on the compression behaviour of stiff-ened plates[J]. Journal of Constructional Steel Research, 2006, 62(11): 1087-1100. [12] HUGHES O F, GHOSH B, CHEN Y. Improved prediction of simultaneous local and overall bucking of stiffened panels[J]. Thin-Walled Structures, 2004, 42(6): 827-856. [13] CHOU C C, UANG C M, SEIBLE F. Experimental evalu-ation of compressive behavior of orthotropic steel plates for the new San Francisco-Oakland Bay Bridge[J]. Journal of Bridge Engineering, 2006, 11(2): 140-150. [14] 康孝先. 大跨度钢桥极限承载力计算理论与试验研究[D]. 成都: 西南交通大学, 2009.KANG Xiao-xian. Calculation theories and tests research on the ultimate capacity of the long-span steel bridges[D]. Chengdu: Southwest Jiaotong University, 2009. (in Chinese). [15] 吴冲, 曾明根, 冯凌云. 苏通大桥正交异性板局部模型极限承载力试验[J]. 桥梁建设, 2006(2): 21-23, 35. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS200602006.htmWU Chong, ZENG Ming-gen, FENG Ling-yun. Local part model test for ultimate bearing capacity of orthotropic panel of Sutong Bridge[J]. Bridge Construction, 2006(2): 21-23, 35. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS200602006.htm -





 下载:
下载: