基于复杂网络的城市路网结构分析方法

ZHANG Wei-hua; YANG Bo; CHEN Jun-jie

doi:10.19818/j.cnki.1671-1637.2012.05.009

基于复杂网络的城市路网结构分析方法

doi: 10.19818/j.cnki.1671-1637.2012.05.009

合肥工业大学交通运输工程学院, 安徽合肥 230009

基金项目:

National Natural Science Foundation of China 51178158

Special Fund for Basic Scientific Research of Ceatral Colleges 2010HGZY0010

详细信息

中图分类号: U491.13
计量
- 文章访问数: 1124
- HTML全文浏览量: 106
- PDF下载量: 1485
- 被引次数: 0
出版历程
- 收稿日期: 2012-05-22

Analysis method of urban road network structure based on complex network

School of Transportation Engineering, Hefei University of Technology, Hefei 230009, Anhui, China

Funds:

National Natural Science Foundation of China 51178158

Special Fund for Basic Scientific Research of Ceatral Colleges 2010HGZY0010

More Information

Author Bio:
ZHANG Wei-hua(1967-), Male, Anqing, Anhui, Professor of Hefei University of Technology, PhD, Researchon UrbanTraffic Planning, +86-551-2901960, hfutits@163.com

Article Text (Baidu Translation)

摘要

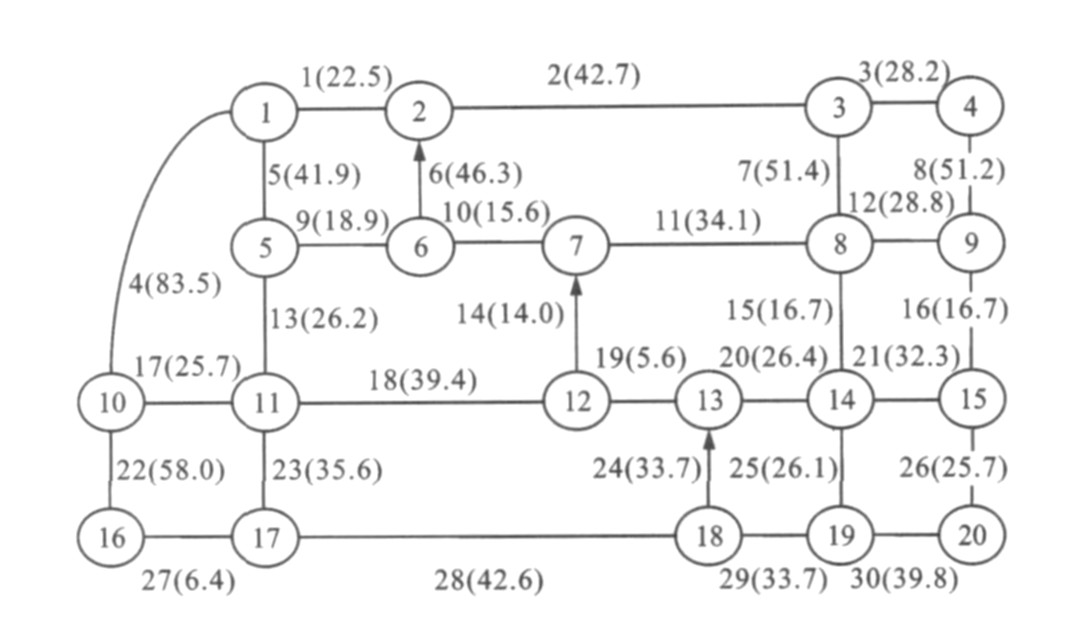
摘要: 在城市道路网络的基础上, 探讨了应用复杂网络理论的可行性和有效性。运用Dijkstra最短路径算法和Space L方法建立初始拓扑网络, 并建立了节点度、边度和节点路阻的特性指标模型。在反映路网功能真实性的前提下, 优化了拓扑网络, 并以某市中心城区道路交通数据为例进行实例分析。分析结果表明: 在初始网络中, 节点度数的均值为2.850 0, 标准差为0.670 8;节点路阻的平均值为84.680 0 s, 标准差为11.768 8 s;在优化网络中, 节点度数的均值为38.750 0, 标准差为24.683 0, 节点路阻的平均值为91.780 0 s, 标准差为18.862 8 s;东西向边的平均度数为42.00, 南北向边的平均度数为29.86, 内部边的平均度数为55.00, 外部边的平均度数为28.33。在优化网络中, 当度数较大的节点在路网中失稳时, 在非拥挤状态下, 最短路径路阻增大, 而在拥挤状态下, 网络会瘫痪。度数较大的节点与真实路网中交叉口重要程度相符, 能够体现交叉口重要程度的差异性。
- 交通规划 /
- 城市路网 /
- 最短路径 /
- 复杂网络 /
- Dijkstra算法 /
- SpaceL方法
Abstract: Based on urban road network, the feasibility and effectiveness of complex network theory application were analyzed.By using Dijkstra shortest path algorithm and Space L method, the initial topology network was built, and the characteristic index models of the degree of node, the degree of edge and the road impedance of node were set up.Under the premise of reflecting the reality of road network function, the initial topology network was optimized, and empirical analysis was carried out by using road traffic data in a central urban area.Analysis result shows that in the initial topology network, the average node degree is 2.850 0 and the standard deviation of node degree is 0.670 8.The average road impedance of node is 84.680 0 s and the standard deviation is 11.768 8 s.While in the optimal topology network, the average node degree is 38.750 0 and the standard deviation of node degree is 24.683 0.The average road impedance of nodes is 91.780 0 s and the standard deviation is 18.862 8 s.The average degree of east-west road section is 42.00, the average degree of north-south road section is 29.86, the average degree of internal section is 55.00, and the average degree of external road section is 28.33.In the optimal topology network, when the node with large degree is not stable, the road impedance of shortest path will increase in non-crowded state, and the road network will be paralyzed in crowded state.The node with higher degree is accord with the importance degree of intersection in real road network, and the difference of importance degree for intersection can be more reflected.
- traffic engineering /
- urban road network /
- shortest path /
- complex network /
- Dijkstra algorithm /
- Space L method

HTML全文

Figure 1. Initial topology network

下载: 全尺寸图片幻灯片

Figure 2. Road impedances of nodes

下载: 全尺寸图片幻灯片

Figure 3. Average lengths of edges

下载: 全尺寸图片幻灯片

Figure 4. Degrees of nodes

下载: 全尺寸图片幻灯片

Figure 5. Retlationship between degree and road impedance for node

下载: 全尺寸图片幻灯片

Figure 6. Distribution of edge degrees among different nodes

下载: 全尺寸图片幻灯片

Figure 7. Distribution of edge degrees among different nodes

下载: 全尺寸图片幻灯片

Table 1. Minimum road impedances s

Node	1	2	3	4	5	6	7	8	9	10
1	0.0	22.5	65.2	93.4	41.9	60.8	76.4	110.5	139.3	83.5
2	22.5	0.0	42.7	70.9	64.4	46.3	61.9	94.1	122.1	106.0
3	65.2	42.7	0.0	28.2	107.1	89.0	85.5	51.4	79.4	148.7
4	93.4	70.9	28.2	0.0	135.3	117.2	113.7	79.6	51.2	176.9
5	41.9	64.4	107.1	135.3	0.0	18.9	34.5	68.6	97.4	51.9
6	60.8	83.3	101.1	129.3	18.9	0.0	15.6	49.7	78.5	70.8
7	76.4	98.9	85.5	113.7	34.5	15.6	0.0	34.1	62.9	79.1
8	110.5	94.1	51.4	79.6	68.6	49.7	34.1	0.0	28.8	113.2
9	139.3	122.1	79.4	51.2	97.4	78.5	62.9	28.8	0.0	142.0
10	83.5	106.0	140.8	176.9	78.9	97.8	113.4	40.8	169.6	0.0

下载: 导出CSV

Table 2. Node sequences

Node	1	2	3	4	5	6	7	8	9	10
1		2, 1	3, 2, 1	4, 3, 2, 1	5, 1	6, 5, 1	7, 6, 5, 1	8, 7, 6, 5, 1	9, 8, 7, 6, 5, 1	10, 1
2	1, 2		3, 2	4, 3, 2	5, 1, 2	6, 2	7, 6, 2	8, 3, 2	9, 4, 3, 2	10, 1, 2
3	1, 2, 3	2, 3		4, 3	5, 1, 2, 3	6, 2, 3	7, 8, 3	8, 3	9, 4, 3	10, 1, 2, 3
4	1, 2, 3, 4	2, 3, 4	3, 4		5, 1, 2, 3, 4	6, 2, 3, 4	7, 8, 3, 4	8, 3, 4	9, 4	10, 1, 2, 3, 4
5	1, 5	2, 5	3, 2, 1, 5	4, 3, 2, 1, 5		6, 5	7, 6, 5	8, 7, 6, 5	9, 8, 7, 6, 5	10, 11, 5
6	1, 5, 6	2, 1, 5, 6	3, 8, 7, 6	4, 3, 8, 7, 6	5, 6		7, 6	8, 7, 6	9, 8, 7, 6	10, 11, 5, 6
7	1, 5, 6, 7	2, 1, 5, 6, 7	3, 8, 7	4, 3, 8, 7	5, 6, 7	6, 7		8, 7	9, 8, 7	10, 11, 12, 7
8	1, 5, 6, 7, 8	2, 3, 8	3, 8	4, 3, 8	5, 6, 7, 8	6, 7, 8	7, 8		9, 8	10, 11, 12, 7, 8
9	1, 5, 6, 7, 8, 9	2, 3, 4, 9	3, 4, 9	4, 9	5, 6, 7, 8, 9	6, 7, 8, 9	7, 8, 9	8, 9		10, 11, 12, 7, 8, 9
10	1, 10	2, 1, 10	3, 2, 1, 10	4, 3, 2, 1, 10	5, 11, 10	6, 5, 11, 10	7, 6, 5, 11, 10	8, 7, 12, 11, 10	9, 8, 14, 13, 12, 11, 10

下载: 导出CSV

Table 3. Degrees of nodes and average impedances

Network	Degree of node		Road impendance of node
Network	Average value	Standard deviation	Average value/s	Standard deviation/s
Optimal network	38.750 0	24.683 0	91.780 0	18.862 8
Initial network	2.850 0	0.670 8	84.680 0	11.768 8

下载: 导出CSV

Table 4. Degrees of edges among different nodes

参考文献(15)

[1]	GUO Ji-fu, GAO Yong, WEN Hui-min. Assessment methodology of connect reliability based on substituted route[J]. Journal of Highway and Transportation Research and Development, 2007, 24(7): 91-94.
[2]	CHEN A, YANG Hai, LO H K, et al. Capacity reliability of a road network: an assessment methodology and numerical results[J]. Transportation Research Part B: Methodological, 2002, 36(3): 225-252. doi: 10.1016/S0191-2615(00)00048-5
[3]	CHEN A, YANG Hai, LO H K, et al. A capacity related reliability for transportation networks[J]. Journal of Advanced Transportation, 1999, 33(2): 183-200. doi: 10.1002/atr.5670330207
[4]	WATTS D J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440-442. doi: 10.1038/30918
[5]	BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. doi: 10.1126/science.286.5439.509
[6]	ALBERT R, BARABASI A L. Statistical mechanics of complex networks[J]. Reviews Modern Physics, 2002, 74(1): 47-97. doi: 10.1103/RevModPhys.74.47
[7]	JIANG Bing, CLARAMUNT C. A structural approach to the model generalisation of an urban street network[J]. Geoinformatical, 2004, 8(2): 157-171. doi: 10.1023/B:GEIN.0000017746.44824.70
[8]	PORTA S, CRUCITT I P, LATORA V. The network analy-sis of urban streets: a dual approach[J]. Physica A, 2006, 369(2): 853-866. doi: 10.1016/j.physa.2005.12.063
[9]	LAMMER S, GEHLSEN B, HELBIG D. Scaling laws in the spatial structure of urban road networks[J]. Physica A, 2006, 363(1): 89-95. doi: 10.1016/j.physa.2006.01.051
[10]	LATORA V, MARCHIORI M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(1): 1-4.
[11]	ANDREA D M, MARC B, ALESSANDRO C, et al. The structure of inter-urban traffic: a weighted network analysis[J]. Environment and Planning B: Planning and Design, 2007, 34(5): 905-924. doi: 10.1068/b32128
[12]	GAO Zi-you, WU Jian-jun, MAO Bao-hua, et al. Study onthe complexity of traffic networks and related problems[J]. Journal of Transportation Systems Engineering and Informa-tion Technology, 2005, 5(2): 79-83.
[13]	GAO Zi-you, LI Ke-ping, LI Xin-gang, et al. Scaling laws of the network traffic flow[J]. Physica A, 2007, 380(1): 577-584.
[14]	JIANG Bing. A topological pattern of urban street networks: universality and peculiarity[J]. Physica A, 2007, 384(2): 647-655.
[15]	MA Jia-qi, BAI Yan, HAN Bao-ming. Characteristic analysis of basic unit and complex network for urban rail transit[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 65-70.