突发灾害下交通控制与VMS协同技术

林赐云; 龚勃文; 赵丁选; 刘雪莲

doi:10.19818/j.cnki.1671-1637.2012.06.016

突发灾害下交通控制与VMS协同技术

doi: 10.19818/j.cnki.1671-1637.2012.06.016

林赐云^{1, 2,},
龚勃文^{1, 2},
赵丁选^{1, 3},
刘雪莲⁴

1.
吉林大学汽车仿真与控制国家重点实验室，吉林长春 130012
2.
吉林大学交通学院，吉林长春 130012
3.
吉林大学机械科学与工程学院，吉林长春 130012
4.
宁波工程学院机械工程学院，浙江宁波 315211

基金项目:

国家863计划项目 2009AA11Z218

高等学校博士学科点专项科研基金项目 20110061120043

中国博士后科学基金项目 2011M500615

中国博士后科学基金项目 20100481054

中国博士后科学基金项目 2012T50300

浙江省教育厅科研基金项目 Y201224940

详细信息

作者简介:
林赐云(1980-), 男, 福建漳州人, 吉林大学讲师, 工学博士, 从事智能交通控制研究

中图分类号: U491
计量
- 文章访问数: 942
- HTML全文浏览量: 185
- PDF下载量: 856
- 被引次数: 0
出版历程
- 收稿日期: 2012-07-18
- 刊出日期: 2012-12-25

Traffic control and VMS collaborative technique in sudden disaster

LIN Ci-yun^{1, 2
,},
GONG Bo-wen^{1, 2},
ZHAO Ding-xuan^{1, 3},
LIU Xue-lian⁴

1.
State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130012, Jilin, China
2.
School of Traffic, Jilin University, Changchun 130012, Jilin, China
3.
School of Mechanical Science and Engineering, Jilin University, Changchun 130012, Jilin, China
4.
School of Mechanical Engineering, Ningbo University of Technology, Ningbo 315211, Zhejiang, China

More Information

Author Bio:
LIN Ci-yun(1980-), male, lecturer, PhD, +86-431-85095591, linciyun@jlu.edu.cn

Article Text (Baidu Translation)

摘要

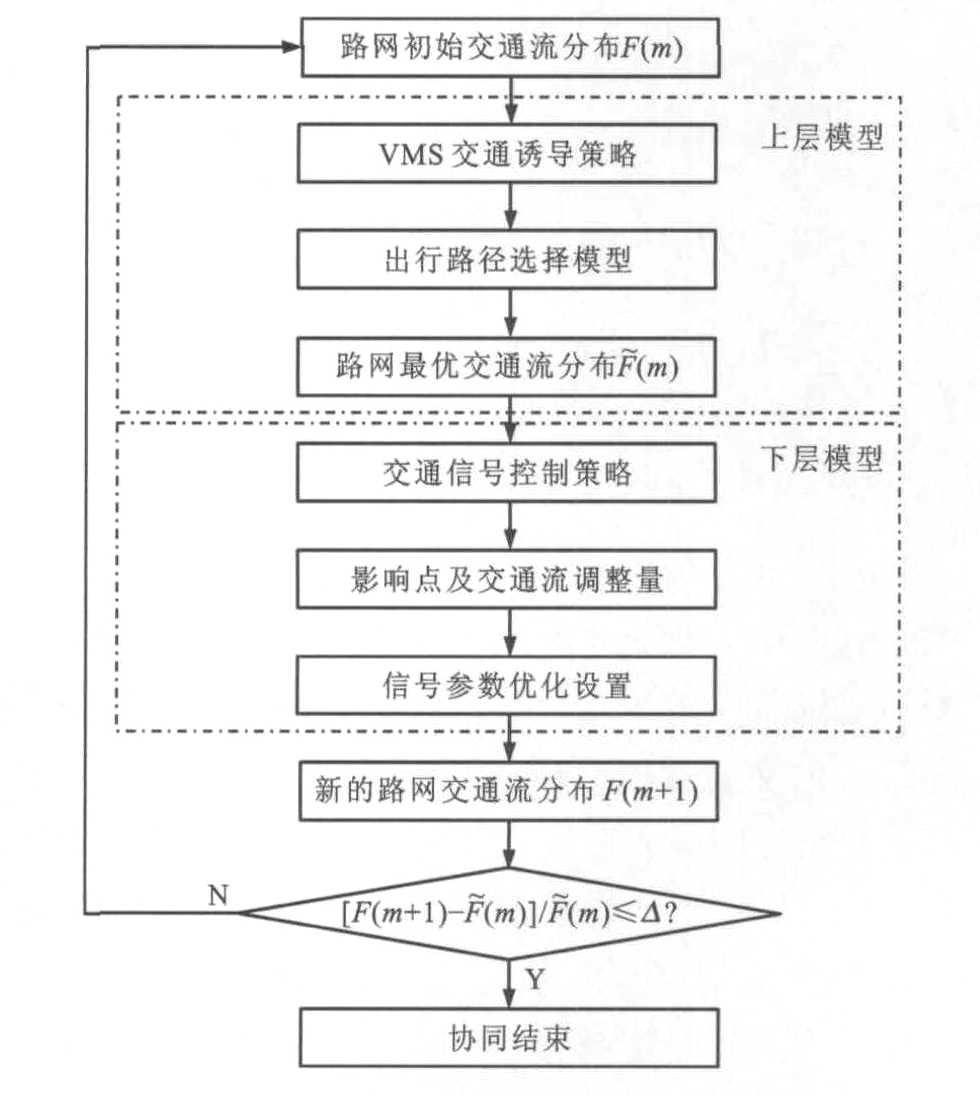
摘要: 估计了可变信息板(VMS)的影响范围, 构建了交通控制与VMS的协同一体化模型。通过VMS影响驾驶人的出行路径选择行为, 引导路网交通流向最优交通流分布模式发展。通过交通控制调整交叉口信号参数, 实现路网交通流的截流与分流, 最终形成路网交通流最优交通分布模式。采用Frank-Wolfe均衡分配和遗传算法相结合对模型进行优化求解, 利用Paramics API开发模型和算法。以Paramics软件为仿真平台, 以山东省淄博市淄博新区为模拟路网, 在路网突发灾害下对模型和算法进行了验证。验证结果表明: 路网饱和度越大, 构建的模型相对于Synchro模型, 提高路网交通流运行性能指标的效果越明显, 促进路网交通流稳定性的能力越强, 越能均衡分配路网负载。当受灾交通流疏散完成80%, 路网连线饱和度分别为不大于0.8, 大于0.8且不大于1.0, 大于1.0时, 相比Synchro模型, 构建模型的受灾交通流疏散时间分别减少11.55、21.84、25.64min, 疏散速度分别提高25.98%、31.83%、20.16%。
- 交通控制 /
- 协同优化 /
- 双层规划 /
- 可变信息板 /
- 突发灾害
Abstract: The influence scope of variable message signs(VMS) was estimated, and a collaborative model integrated of traffic control and VMS was constructed. The route choice behavior of driver was impacted by VMS, and the development of network traffic flow was guided by VMS to the optimization distribution mode. The interception and shunt of network traffic flow were fulfilled by adjusting intersection signal parameters in traffic control to form an optimal traffic flow distribution mode. The model was optimized and solved by combining Frank-Wolfe equilibrium assignment and genetic algorithm. The model and algorithm were developed by using Paramics API. In the condition of network with burst disaster, the model and algorithm were verified by taking software Paramics as simulation platform and Zibo New District of Shandong Province as simulation network. Verified result shows that with the increase of road network saturation, compared with Synchro model, the effect of the model is more obvious in improving performance indexes of road network traffic flow, the ability promoting the stability of road network's traffic flow is stronger, and the equilibrium assignment ability of road network loading is better. When the evacuation of traffic flow for sudden disaster completes 80%, and the link saturations of road network are not more than 0.8, between 0.8 and 1.0, more than 1.0 respectively, compared with Synchro model, the evacuation times respectively decrease by 11.55, 21.84, 25.64 min, the evacuation speed respectively increase by 25.98%, 31.83%, 20.16%.
- traffic control /
- collaborative optimization /
- bi-level programming /
- variable message signs /
- sudden disaster

HTML全文

图 1 模型框架

Figure 1. Model framework

下载: 全尺寸图片幻灯片

图 2 模拟路网

Figure 2. Simulation network

下载: 全尺寸图片幻灯片

图 3 疏散百分比与时间关系

Figure 3. Relationship of evacuated percentage and time

下载: 全尺寸图片幻灯片

表 1 对比结果

Table 1. Comparison results

饱和度	模型	平均延误/s	标准偏差	平均速度/(km·h^-1)	标准偏差	交叉口饱和度	标准偏差	排队长度/m	标准偏差
λ_a≤0.8	Synchro	5.241	2.041	45.320	6.773	0.621	0.142	6.533	6.179
λ_a≤0.8	TCVMS	5.112	1.724	46.170	5.465	0.611	0.101	6.527	5.491
0.8 < λ_a≤1.0	Synchro	24.320	6.317	35.840	9.194	0.860	0.201	18.960	4.234
0.8 < λ_a≤1.0	TCVMS	22.310	5.256	38.420	7.851	0.833	0.193	15.350	4.211
λ_a > 1.0	Synchro	37.290	5.542	25.160	4.527	0.939	0.114	36.470	7.712
λ_a > 1.0	TCVMS	34.230	4.437	28.130	3.699	0.905	0.102	33.620	6.985

下载: 导出CSV

参考文献(20)

[1]	GHODS A H, FU L, RAHIMI-KIAN A. An efficient opti-mization approach to real-time coordinated and integrated freeway traffic control[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(4): 873-884. doi: 10.1109/TITS.2010.2055857
[2]	WU Xin-kai, LIU H X, GEROLIMINIS N. An empirical analy-sis on the arterial fundamental diagram[J]. Transportation Research Part B: Methodological, 2011, 45(1): 255-266. doi: 10.1016/j.trb.2010.06.003
[3]	GARTNER N H, STAMATIADIS C. Integration of dynamic traffic assignment with real-time traffic adaptive control system[J]. Transportation Research Record, 1998(1644): 150-156.
[4]	ABDELFATAH A S, MAHMASSANI H S. System optimal time-dependent path assignment and signal timing in traffic network[J]. Transportation Research Record, 1998(1645): 185-193.
[5]	LO H K. A cell-based traffic control formulation: strategies and benefits of dynamic timing plans[J]. Transportation Science, 2001, 35(2): 148-164. doi: 10.1287/trsc.35.2.148.10136
[6]	VARIA H R, DHINGRA S L. Dynamic optimal traffic assignment and signal time optimization using genetic algorithms[J]. Computer-Aided Civil and Infrastructure Engineering, 2004, 19(4): 260-273. doi: 10.1111/j.1467-8667.2004.00353.x
[7]	UKKUSURI S V, RAMADURAI G, PATIL G. A robust transportation signal control problem accounting for traffic dynamics[J]. Computers and Operations Research, 2010, 37(5): 869-879. doi: 10.1016/j.cor.2009.03.017
[8]	KAROONSOONTAWONG A, WALLER S T. Integrated network capacity expansion and traffic signal optimization problem: robust bi-level dynamic formulation[J]. Networks and Spatial Economics, 2010, 10(4): 525-550. doi: 10.1007/s11067-008-9071-x
[9]	MITSAKIS E, SALANOVA J M, GIANNOPOULOS G. Combined dynamic traffic assignment and urban traffic con-trol models[J]. Procedia Social and Behavioral Sciences, 2011(20): 427-436.
[10]	卢守峰. 基于元胞自动机的交通信号控制与路径诱导的协同研究[D]. 长春: 吉林大学, 2006. LU Shou-feng. The study on combined traffic signal control and route guidance based on cellular automata[D]. Chang-chun: Jilin University, 2006. (in Chinese).
[11]	杨庆芳, 杨朝. 基于Q-学习算法的交通控制与诱导协同模式的在线选择[J]. 吉林大学学报: 工学版, 2010, 40(5): 1215-1219. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201005010.htm YANG Qing-fang, YANG Chao. On-line selection method of the traffic control and route guidance collaboration mode based on Q-learning algorithm[J]. Journal of Jilin University: Engineering and Technology Edition, 2010, 40(5): 1215-1219. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY201005010.htm
[12]	崔后盾. 信号控制与VMS诱导的协同策略及信息发布的优化[D]. 北京: 北京交通大学, 2012. CUI Hou-dun. The coordination strategy between signal control and VMS and optimization for information publishing[D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese).
[13]	CHATTERJEE K, HOUNSELL N B, FIRMIN P E, et al. Driver response to variable message sign information in London[J]. Transportation Research Part C: Emerging Technologies, 2002, 10(2): 149-169. doi: 10.1016/S0968-090X(01)00008-0
[14]	尚华艳, 黄海军, 高自友. 可变信息标志诱导下的路径选择行为[J]. 系统工程理论与实践, 2009, 29(7): 166-172. doi: 10.3321/j.issn:1000-6788.2009.07.022 SHANG Hua-yan, HUANG Hai-jun, GAO Zi-you. Route choice behavior under guidance of variable message signs[J]. Systems Engineering—Theory and Practice, 2009, 29(7): 166-172. (in Chinese). doi: 10.3321/j.issn:1000-6788.2009.07.022
[15]	LEE C, RAN B, YANG F, et al. A hybrid tree approach to modeling alternate route choice behavior with online informa-tion[J]. Journal of Intelligent Transportation Systems: Tech-nology, Planning, and Operations, 2010, 14(4): 209-219. doi: 10.1080/15472450.2010.516229
[16]	TAY R, DEB A. Effectiveness of road safety messages on variable message signs[J]. Journal of Transportation Sys-tems Engineering and Information Technology, 2010, 10(3): 18-23. doi: 10.1016/S1570-6672(09)60040-4
[17]	HENDERSON J M. A planning model for optimizing loca-tions of changeable message signs[D]. Waterloo: University of Waterloo, 2004.
[18]	CHEN L W, HU T Y. Dynamic flow equilibrium for flow-responsive signal settings and time-dependent traffic assign-ment[C]∥IEEE. Proceedings of the12th International IEEE Conference on Intelligent Transportation Systems. Saint Louis: IEEE, 2009: 615-620.
[19]	李润梅, 李伟. 饱和路网中动态交通分配和控制一体化建模研究[J]. 信息与控制, 2004, 33(6): 641-645. doi: 10.3969/j.issn.1002-0411.2004.06.001 LI Run-mei, LI Wei. The integrative modeling of dynamic traffic assignment and traffic control in saturated networks[J]. Information and Control, 2004, 33(6): 641-645. (in Chinese). doi: 10.3969/j.issn.1002-0411.2004.06.001
[20]	KIM E Y, KIN S C, SEONG B S. Structure of attractive and repulsive hard-core Yukawa fluids: density functional perturbation theory[J]. Fluid Phase Equilibria, 2011, 308(1/2): 90-97.