0.   引言

随着城市经济的飞速发展, 传统交通模式在现代交通中遇到了越来越多的问题与挑战。为了缓解当前交通网络面临的巨大压力, 如交通拥堵、交通事故等, 智能交通系统(Intelligent Transportation System, ITS) 被引入到动态交通管理中, 并得到了快速发展。作为智能交通系统中的重要组成单元, 短时交通流预测在城市交通管理系统(Urban Transportation Management, UTM) 中始终占有重要地位, 对于更好地分析路网交通状况, 优化交通网络规划和控制策略都有十分重要的意义。

近几十年来, 很多研究人员致力于交通流数据的分析, 并建立了多种交通流预测模型。一般来说, 已有的交通流预测方法可以分为两类: 基于时间序列的预测方法与基于时空联合的预测方法。基于时间序列的预测方法将交通流看作是单一的时间序列, 利用信号处理的方法对交通流数据进行分析和预测。早在20世纪90年代, Voort等就研究了ARIMA模型在交通流预测上的应用^[1]; 近年来, Williams等研究了交通流的周期性, 并利用季节性ARIMA模型进行短时预测^[2]。此外, Kalman滤波方法也在交通流的预测问题上得到了广泛应用^[3]。陈相东等研究了基于局部多项式拟合的交通流预测方法^[4]; Zhang等将模糊逻辑系统理论应用于交通流预测^[5]。随着智能计算的发展, 神经网络也越来越多的被用于交通流预测。Zheng等研究了使用贝叶斯模型与神经网络模型联合对高速路交通流进行短时预测的方法^[6]。时空联合的预测方法大多是考虑了上游交通路段对当前路段交通流的影响, 将上游路段与当前路段的历史交通数据作为模型的输入, 来计算当前路段的交通流预测值, 例如: 矢量ARIMA的空间模型将路段上游观测点的交通流量利用速度关系和当前观测点联系起来^[7]; 基于贝叶斯网络的预测方法用贝叶斯图模型学习上下游交通流量的关系模型^[8]; 基于上游交通数据的多层感知(Multilayer Perceptron, MLP) 预测方法^[9]; 基于高斯过程的交通流预测模型^[10]等。此外, 采用交通流的空间推理模型也应用于交通流的预测^[11]。以上基于统计学习的方法模型复杂, 需要优化的参数过多, 计算量较大, 不适合交通系统的实时计算。

目前的方法大多基于时空关系预测当前路段或者某个观测点的未来交通流, 但是在实际应用中, 往往会遇到这样一个问题, 该路段或者观测点并没有上游观测值的存在, 只能利用本观测点的历史信息进行时间序列上的预测。在Xu等的研究中^[11], 就需要首先预测输入整个交通网络的流量, 因此, 针对时间序列上的交通流预测目前依旧是至关重要的。作为典型的非线性时间序列, 分类学习的方法也被越来越多使用于交通流的预测。基于对交通流数据进行训练、预测的思想, 本文使用分类回归树模型进行高速路交通流的短时预测。首先, 对已有历史交通流数据进行分析学习, 建立一个完备的模型树, 使模型树中能够尽量完整地包含历史数据与预测数据之间的非线性关系; 其次, 把当前交通数据作为模型的输入值, 预测未来15 min的交通流量。在试验过程中采用了美国波特兰州高速路网的真实数据对提出的模型进行测试。

1.   分类回归树模型简介

在数据挖掘与机器学习中, 回归算法是解决预测问题的一种有效的核心工具。通过比较不同算法在回归问题中建立的学习模型, 可将这些算法分为基于线性模型的回归算法、基于K近邻(K-nearest Neighbor, KNN) 模型的回归算法、基于树模型的回归算法和一些其他模型算法(人工神经网络ANN、支持向量机SVM等)。其中K近邻模型^[12-13]、人工神经网络^[14]、支持向量机^[15]等已在智能交通系统中得到了广泛应用, 其中樊娜等将非参数回归模型和BP神经网络模型组合为混合预测模型对短时交通流进行预测^[16]。作为机器学习中一种经典的基于决策树模型的数据处理方法, 分类回归树(Classification and Regression Tree, CART)通过递归划分, 可以用于对连续变量进行预测(回归)以及对不连续的变量类别进行预测(分类)。在本文交通流短时预测问题研究中, 采用分类回归树模型对每15 min的交通流量数据进行预测。

经典的CART模型是由Breiman等于1984年提出并推广的一种决策树分类方法, 是对数据空间进行递归划分并针对每一个节点建立一个回归预测模型。在回归树中, 以序列的均方误差作为是否对序列继续划分的标准。CART是基于下面2个关键的思想: 第1个是关于递归划分自变量空间的想法; 第2个是为了防止过拟合的发生, 用验证数据进行剪枝。

1.1   分类回归树的结构

递归划分或者树的生长策略主要分为3个问题: 首先是选择分类变量的标准; 其次要找到被选择变量的分裂点的标准; 最后是确定合适停止树生长过程的标准。交通流量的预测问题实质上是找到一组由输入变量X和输出变量y组成的对应关系: 在参数模型中往往是一个固定的函数拟合; 在非参数模型中是一系列的数学关系模型。本文中假定X为模型中的自变量, 即模型的输入变量, y为目标变量(模型的输出, 即需要预测的t+1时刻的交通流量v_t+1), 在交通流预测问题上, 本文将X_t定义为t时刻的交通流量

$X{}_t=\{v{}_{t-i}i=0,1,\cdots ,d\}(1)$

式中: v_t-i为t-i时刻的交通流量。

对于包含有N个训练样本的训练样本库Γ, 可以定义为

$\Gamma =\{(X{}_t,y{}_t)t=1,2,\cdots ‚{\rm N}\}(2)$

本文的目标是在给定一个新的自变量X后再预测y的值, 这就需要不同的划分原则。理论上, 一个很简单的做法就是把训练样本库Γ根据其不同数值特征划分为K个不同的子集A₁、A₂、…、A_K, 当j时刻新的交通状态X_j根据其数值特征被判定为属于集合A_k时, 利用集合A_k所对应的规则来计算出y_j, 并将其作为预测值, 这就是回归树用于序列预测的基本思想^[17]。

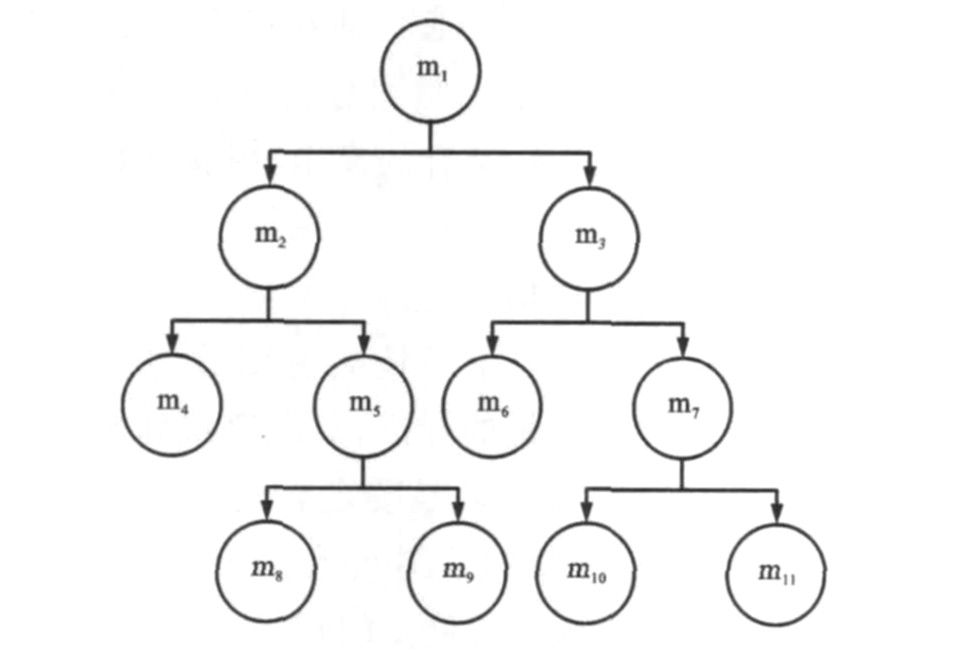
分类回归树是通过依次把训练样本库Γ按照一定规则分裂成两部分而建立起来的, 结构见图 1, 其中: m₁为树的根节点, 包含全部训练样本Γ; 节点m₂、m₃、m₅、m₇为树模型中的中间节点; m₄、m₆、m₈、m₉、m₁₀、m₁₁为叶节点, 对应于最终分裂后的集合A₁、A₂、…、A_K, 即表示该节点的纯度已经达到预定要求, 不再往下分裂。图 1中子节点m₂、m₃由父节点m₁分裂而成, 同时又作为父节点继续分裂, 直至节点纯度达到预定要求。

图  1  分类回归树模型结构

Figure  1.  Structure of classification and regression tree model

下载: 全尺寸图片 幻灯片

1.2   分类回归树分裂准则

在分类回归树的生长过程中, 节点的分裂准则决定了当前节点是否继续分裂为2个子节点。在模型建立之前, 首先设定合适的决定节点是否分裂的纯度阈值δ与最小样本数量n, 使得树模型能够准确、完整的对训练数据进行分类。

Step 1:选取特征值, 从训练样本数据的d+1个特征中选取合适的特征值, 使在该特征值下的分裂能最大化地对节点上的样本进行分类。

Step 2:搜索样本空间, 找到使下一代子节点中数据集的纯度最小的最优分裂变量, 将本节点数据序列分为2个子集。

Step 3:在第l个特征值下, 计算数据序列纯度是否小于δ, 或者样本数量是否小于n, 确定是否进行分裂。其中, 使用序列在归一化之后的方差来计算纯度。

Step 4:如不能继续分裂, 则将该节点记为叶节点, 进而使用该叶节点样本集合的自变量X与目标变量y建立线性拟合模型f(X), 如还需要继续分裂则转到Step 1。

本文中的纯度阈值采用均方误差MSE来计算

$\delta =(y-\stackrel{\wedge }{{\displaystyle y}}){}^2(3)$

式中: $\stackrel{\wedge }{{\displaystyle y}}$为y的估计值。

1.3   分类回归树剪枝

当一个数据集在建立树模型时产生了大量的叶节点, 就有可能发生过拟合现象, 从而导致模型失效。本文采用交叉验证的思想来判定节点的数据集是否过拟合, 这一判定并消除过拟合现象的方法称之为分类回归树的剪枝。

树模型的剪枝可以在训练过程中进行也可以在树生长停止后进行, 例如Chi-平方自动交互检测就是通过显著性去评估对某一节点分裂是否能提高分类纯度, 如果不能显著提高, 就不进行划分, 然而, 在树训练过度前就停止并不一定是最好的方法。在CART算法中: 首先将所有样本数据划分为训练集与测试集, 在训练集基础上根据预设参数纯度阈值与最小样本数量生成一个树模型; 其次, 利用测试集数据测试建好的模型树, 依次消除叶节点并计算误差, 如果消除该节点可以降低树模型在测试集上的误差, 就将该叶节点剪枝。具体算法流程如下。

Step 1:在测试集上执行树模型。

Step 2:如果任何一个子节点是树, 在树节点上执行Step 1, 否则执行Step 3。

Step 3:消除2个子节点, 并在测试集上进行测试, 计算预测误差e_s。

Step 4:计算消除节点之前的误差e_o, 如若e_o不小于e_s, 则消除2个子节点, 即对该节点进行剪枝, 否则保留。

2.   数据分析与模型建立

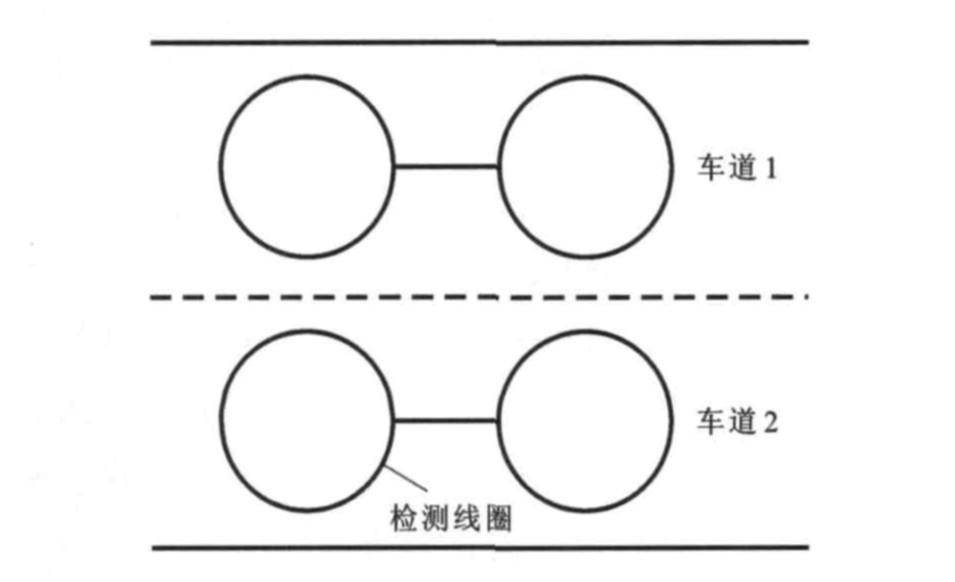
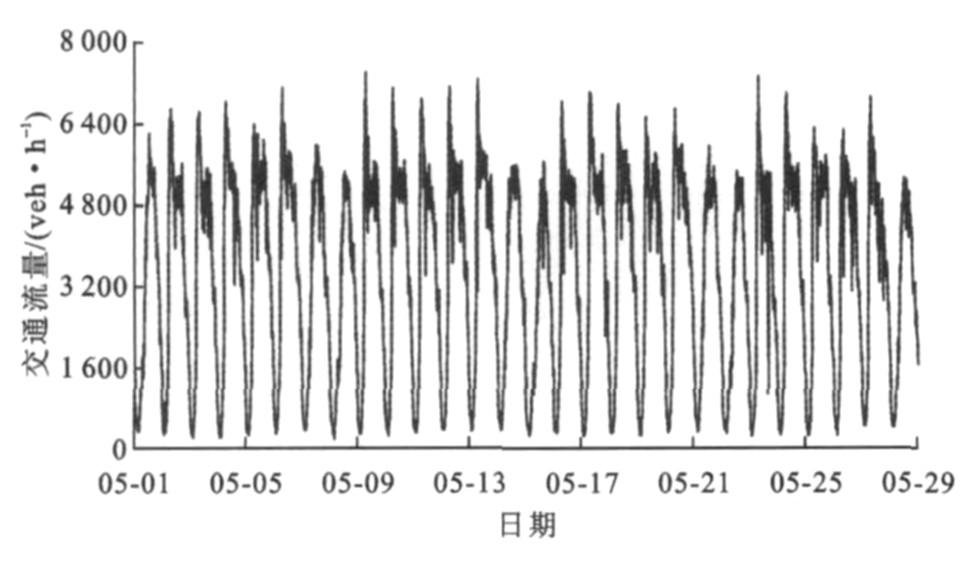
为了测试分类回归树模型在交通流预测问题上的应用效果, 本文采用了波特兰州立大学Portal平台发布的美国波特兰州高速路网交通数据来测试。该交通流量数据是通过在高速路的每个车道上安装检测线圈来获取的, 每20 s计算一次车流量与平均车速。本文采集了波特兰州高速公路I-84上编号为33的交通信息检测站所获取的车流量信息, 见图 2。计算每15 min内的车流量, 训练样本数据持续4周, 从2011-05-01的0:00至2011-05-29的0:00, 共计28天2 688个样本数据, 见图 3。测试样本数据持续一周, 从2011-05-29的0:00至2011-06-05的0:00, 共计7 d 672个样本数据。为了真实反映道路交通拥挤状况, 模型输入的所有流量数据均转换为每小时的平均车流量(veh·h^-1)。

图  2  交通流量检测线圈

Figure  2.  Detecting coils of traffic flow

下载: 全尺寸图片 幻灯片

图  3  训练样本数据

Figure  3.  Training sample data

下载: 全尺寸图片 幻灯片

在建立模型之前, 将时间序列数据变换成交通状态向量空间, 使得2 688个训练数据样本就转换为一个(p+2)×(2 688-p-1)的样本库矩阵。矩阵的每一行(v_t, v_t-1, …, v_t-p, v_t+1)由X_t与y_t组成, 即样本库矩阵的前p+1列是自变量X, 最后一列表示因变量y。而测试集则是(p+2)×(672-p-1)的矩阵, 在模型测试中, 只有前p+1列的矩阵被输入到训练好的模型中, 最后一列作为真实值来测试分类回归树预测模型的准确度。

CART模型建立的预设纯度阈值为2, 叶节点最小样本数量为20。即当节点的误差下降小于2或者该节点含有状态向量数目不大于20时, 将此节点标记为叶节点并停止分裂。在结束树模型剪枝之后, 对每个叶节点的自变量X与目标变量y进行线性拟合, 得到线性函数关系式

$y=f(X)(4)$

这样就形成了以线性模型为叶节点的模型树。在预测过程中, 首先将输入的新的测试数据使用树模型进行分类, 得到与之匹配的叶节点。然后将该叶节点对应的线性模型应用于输入数据X_t, 产生预测数值$\stackrel{\wedge }{{\displaystyle y}}{}_t$。

3.   试验结果分析

为了评估分类回归树模型在交通流短时预测上的效果, 本文同时采用了传统的时间序列预测方法: 差分自回归移动平均模型(Autoregressive Integrated Moving Average, ARIMA)和Kalman滤波预测模型对相同的测试序列进行预测。并采用均方根误差(RMSE)与平方绝对百分比误差(MAPE)2种误差评估方法。RMSE、MAPE计算如下

$\begin{array}{l}E{}_{\text{R}\text{Μ}\text{S}\text{E}}=\left[\frac{1}{{\rm T}}{\displaystyle \sum _{t=1}^{{\rm T}}(}y{}_t-\stackrel{\wedge }{{\displaystyle y}}{}_t)\right]{}^{1/2}(5)\\ E{}_{\text{Μ}\text{A}\text{Ρ}\text{E}}=\frac{1}{{\rm T}}{\displaystyle \sum _{t=1}^{{\rm T}}\frac{y{}_t-\stackrel{\wedge }{{\displaystyle y}}{}_t}{y{}_t}}(6)\end{array}$

式中: T为测试样本数量, 即需要预测的交通流的数目; y_t为交通流量的真实值。

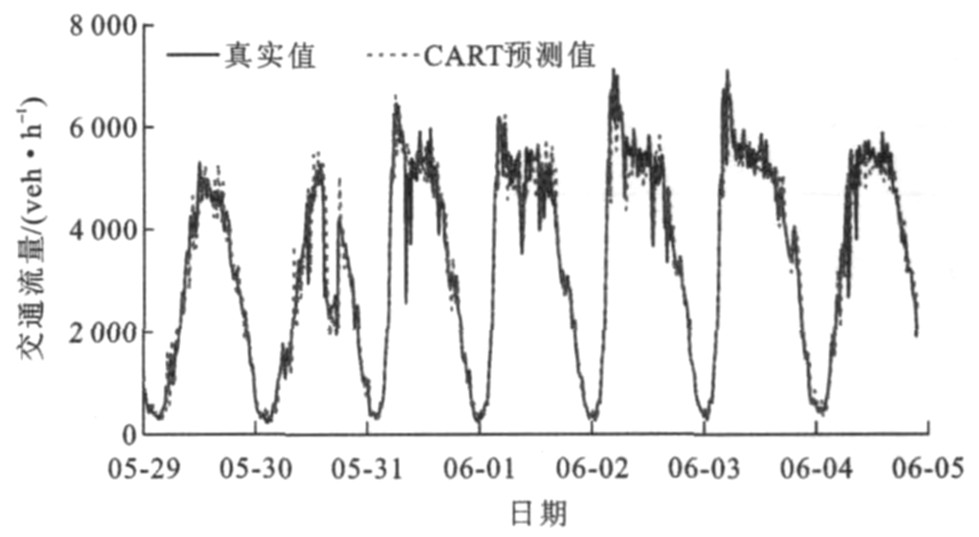
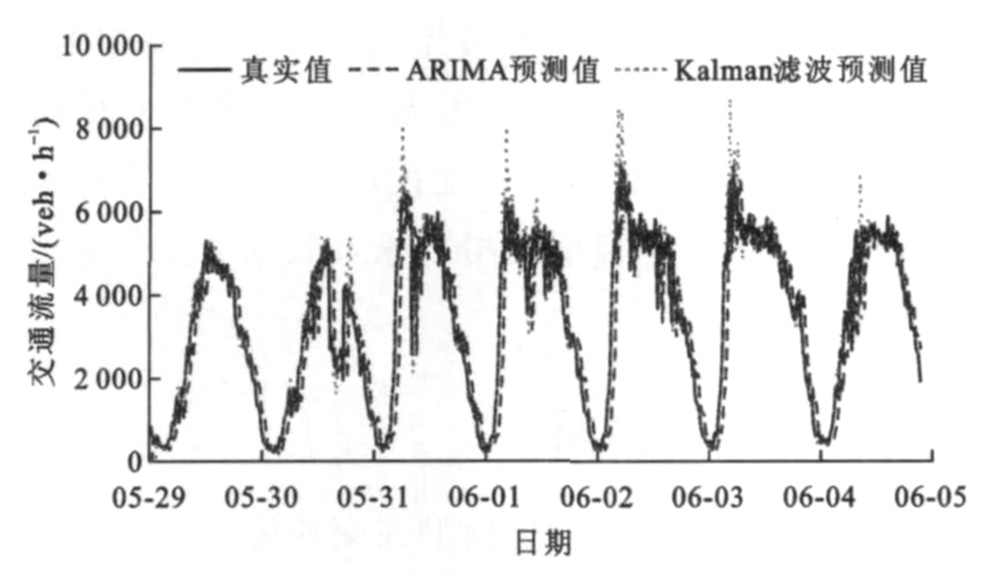
使用CART模型对一周的交通流量进行预测, 结果见图 4。根据文献[12]中非参数方法的试验结果, 在取当前交通状态的20个历史状态邻域, 可以得到满意的试验结果。同样, 将树模型的每个叶节点中含有状态向量的个数限制在至少20个, 以便进行线性回归。同时, 在预剪枝中, 限制每个节点当前误差与在分裂之后的最小误差的差小于100时停止剪枝, 将该节点标记为叶节点。图 5为使用另外2个经典的时间序列模型来对同样的交通流量数据进行预测的结果, 可以看出, 基于CART模型的预测方法能够很好匹配真实值, 虽然在某些极端情况下不能很好的做出正确预测。

图  4  CART模型预测结果

Figure  4.  Prediction result of CART model

下载: 全尺寸图片 幻灯片

图  5  两种模型的预测结果比较

Figure  5.  Prediction results of 2 models

下载: 全尺寸图片 幻灯片

为了对比模型对交通流复杂变化的预测性能, 将6月1日(周三)的预测结果单独提取出来, 见图 6。可以看出, 由于是固定参数模型, ARIMA模型鲁棒性不好, 预测结果滞后严重, 特别是在4:00~6:00这一段流量上升期。Kalman滤波模型在大部分时段表现良好, 但是在一些流量较大时段, 如6:00~6:30期间, 预测结果不稳定, 超出真实值约30%。相比较而言, CART模型的预测结果较为稳定, 不论是在早高峰的上升期还是在晚高峰的下降期, 都能很好地估计真实值的变化。

图  6  6月1日预测结果比较

Figure  6.  Prediction results comparison of June 1

下载: 全尺寸图片 幻灯片

表 1为分别对3种模型预测值与真实值进行误差计算的结果, 可以精确的说明CART模型预测的效果。从对比结果中可以看出基于CART模型的预测方法在测试的一周数据中有4天的RMSE和MAPE均低于ARIMA与Kalman滤波模型。通过一周平均RMSE的比较来看, CART预测模型的精度较ARIMA模型提高了42.1%, 较Kalman滤波模型提高了13.1%。由此看出基于CART的预测模型是一种有效的交通流预测方法。

表  1  三种模型的预测误差对比

Table  1.  Prediction error comparison of 3 models

日期	RMSE			MAPE
	CART模型	ARIMA模型	Kalman滤波模型	CART模型	ARIMA模型	Kalman滤波模型
5月29日	169.76	235.11	133.54	0.118	0.176	0.094
5月30日	273.16	381.20	266.98	0.167	0.307	0.151
5月31日	253.50	474.94	347.96	0.110	0.266	0.145
6月1日	229.86	458.04	278.51	0.111	0.271	0.131
6月2日	255.58	469.94	309.38	0.105	0.234	0.125
6月3日	195.67	427.81	262.34	0.083	0.215	0.103
6月4日	244.47	312.53	267.73	0.124	0.203	0.107
平均值	231.71	394.22	266.63	0.117	0.234	0.123

下载: 导出CSV 

| 显示表格

4.   结语

本文提出了基于分类回归树模型的道路交通流量预测方法, 使用大量的训练样本数据建立了分类回归树模型。在初始模型建立之后, 为了防止模型的过拟合, 采用了树模型剪枝的方法进行修正。在树模型建立之后, 在每个叶节点上利用训练样本数据中的自变量与因变量, 拟合得到线性模型, 从而达到在输入新的自变量后可以对其进行预测的目的。为了验证本文模型的有效性, 采用美国波特兰州某高速路的交通流量数据进行验证, 预测15 min后的交通流量, 并与经典的时间序列方法, ARIMA与Kalman滤波预测模型进行了比较。最终结果表明, 基于CART的预测模型可以有效地对交通流量进行短时预测, 尽管基于CART的模型在高速路网交通流量预测上取得了不错的效果, 但本文在叶节点上采用的是最简单的线性模型, 下一步将探索其他非线性模型, 使其更好地预测更为复杂的交通状态, 如城市路网的交通流量。