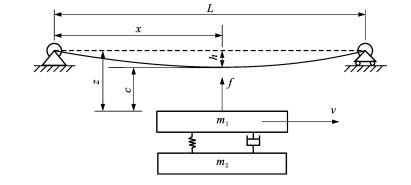
Judgment method of maglev vehicle dynamic stability on flexible track
-
摘要: 分析了EMS型磁浮车辆的动力稳定性, 建立了简化的车轨耦合振动系统动力学模型, 推导了轨道各模态单独作用下系统的时变线性化动力学方程。通过对方程的化简, 得到系统状态矩阵和特征方程的相关系数, 根据系统渐进稳定条件下系数之间的关系, 推导了系统动力稳定应满足的基本条件, 并给出了快速判断动力稳定性的判据。当判据值大于1时, 系统稳定; 当判据值小于1时, 系统不稳定。研究结果表明: 当6种工况的速度分别为100、180、260、340、420、500km·h-1, 抗弯刚度分别为4.83×1010、3.86×1010、3.38×1010、3.38×1010、3.86×1010、4.83×1010 N·m2, 轨道梁长度分别为24.8、22.4、20.4、20.4、22.4、24.8m时, 求得对应的稳定性判据值分别为1.639、0.624、2.339、0.870、3.252、0.571, 对应的Lyapunov特性指数分别为-3.580×10-2、2.443×10-1、-3.910×10-2、1.515×10-1、-5.471×10-2、1.939×10-1, 工况1、3、5的稳定性判据值大于1, 对应的Lyapunov特性指数小于0, 系统是稳定的, 工况2、4、6的稳定性判据值小于1, 对应的Lyapunov特性指数大于0, 系统是不稳定的, 2种判断结果一致, 因此, 提出的判据是有效的。而且稳定性判据解释了随着车辆速度增加而出现共振的原因, 揭示了车辆速度、车轨系统主要参数与磁浮车辆动力稳定性之间的关系, 避免了高维动力学微分方程求解的复杂性, 工程应用简便。Abstract: The dynamic stability of EMS maglev vehicle was analyzed, a simplified dynamics model of vehicle-track coupling vibration system was set up, and the time-varying linear kinetics equations of the system were deduced based on each track mode separately.The state matrix and the correlation coefficients of characteristic equations for the system were produced by simplifying the equations.The basic conditions of the system on dynamic stability were derived from the proper relationship among the coefficients under the condition of asymptotically stable system, and the quick dynamic stability criterion was given.When the criterion value was greater than 1, the system was stable.When the criterion value was less than 1, the system was unstable.Research result indicates that when the speeds of 6kinds of working conditions are 100, 180, 260, 340, 420, 500km·h-1 respectively, the track bending stiffnesses are 4.83×1010, 3.86×1010, 3.38×1010, 3.38×1010, 3.86×1010, 4.83×1010 N·m2 respectively, and the track beam lengths are 24.8, 22.4, 20.4, 20.4, 22.4, 24.8mrespectively, the stability criterion values are1.639, 0.624, 2.339, 0.870, 3.252, 0.571 respectively, and the related Lyapunov characteristic exponents are-3.580×10-2, 2.443×10-1, -3.910×10-2, 1.515×10-1, -5.471×10-2, 1.939×10-1 respectively.Under conditions 1, 3, 5, the stability criterion values are greater than1, the related exponents are less than 0, so the system is stable.Under conditions 2, 4, 6, the stability criterion values are less than 1, the related exponents are greater than 0, so the system is unstable.The two judgment results are coincident, so the criterion is reliable.the stability criterion explains the reason of resonance caused by vehicle speed increase, reveals the relationship among maglev vehicle dynamic stability, vehicle speed and vehicle-track system main parameters, avoids the complexity to solve high-dimension dynamics differential equation, and is simpler and more convenient in engineering application.
-
Key words:
- maglev vehicle /
- dynamics model /
- single-magnet suspension /
- coupling vibration /
- dynamic stability
-
表 1 仿真工况
Table 1. Simulation conditions

表 2 稳定性判据
Table 2. Stability criterions

-
[1] 翟婉明, 赵春发. 磁浮车辆/轨道系统动力学(Ⅰ)――磁/轨相互作用及稳定性[J]. 机械工程学报, 2005, 41(7): 1-10. doi: 10.3321/j.issn:0577-6686.2005.07.001ZHAI Wan-ming, ZHAO Chun-fa. Dynamics of maglev vehicle/guideway systems(Ⅰ)―magnet/rail interaction and system stability[J]. Chinese Journal of Mechanical Engineering, 2005, 41(7): 1-10. (in Chinese) doi: 10.3321/j.issn:0577-6686.2005.07.001 [2] 赵春发, 翟婉明. 磁浮车辆/轨道系统动力学(Ⅱ)――建模与仿真[J]. 机械工程学报, 2005, 41(8): 163-175. doi: 10.3321/j.issn:0577-6686.2005.08.029ZHAO Chun-fa, ZHAI Wan-ming. Dynamics of maglev vehicle/guideway systems(Ⅱ)―modeling and simulation[J]. Chinese Journal of Mechanical Engineering, 2005, 41(8): 163-175. (in Chinese) doi: 10.3321/j.issn:0577-6686.2005.08.029 [3] 李莉, 孟光. 电磁型磁悬浮列车动力学研究综述[J]. 铁道学报, 2003, 25(4): 110-114. doi: 10.3321/j.issn:1001-8360.2003.04.022LI Li, MENG Guang. Summary of the dynamic research on EMS-maglev trains[J]. Journal of the China Railway Society, 2003, 25(4): 110-114. (in Chinese) doi: 10.3321/j.issn:1001-8360.2003.04.022 [4] WANG Kai-yun, HUANG Chao, ZHAI Wan-ming, et al. Progress on wheel-rail dynamic performance of railway curve negotiation[J]. Journal of Traffic and Transportation Engineering: English Edition, 2014, 1(3): 209-220. doi: 10.1016/S2095-7564(15)30104-5 [5] 时瑾, 姚忠达, 王英杰. 轨道梁在磁浮列车以共振速度通过时动力响应分析[J]. 工程力学, 2012, 29(12): 196-203. doi: 10.6052/j.issn.1000-4750.2011.05.0262SHI Jin, YAU J D, WANG Ying-jie. Dynamic response of guideway girders due to high-speed maglev trains moving at resonant speeds[J]. Engineering Mechanics, 2012, 29(12): 196-203. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.05.0262 [6] 曾佑文, 王少华, 张昆仑. EMS磁浮列车-轨道垂向耦合动力学研究[J]. 铁道学报, 1999, 21(2): 21-25. doi: 10.3321/j.issn:1001-8360.1999.02.005ZENG You-wen, WANG Shao-hua, ZHANG Kun-lun. A study of vertical coupling dynamics of EMS maglev train and guideway systems[J]. Journal of the China Railway Society, 1999, 21(2): 21-25. (in Chinese) doi: 10.3321/j.issn:1001-8360.1999.02.005 [7] 梁鑫, 罗世辉, 马卫华, 等. 磁浮列车单铁悬浮车桥耦合振动分析[J]. 交通运输工程学报, 2012, 12(2): 32-37. doi: 10.3969/j.issn.1671-1637.2012.02.006LIANG Xin, LUO Shi-hui, MA Wei-hua, et al. Coupling vibration analysis of single-magnet suspension vehicle-bridge for maglev train[J]. Journal of Traffic and Transportation Engineering, 2012, 12(2): 32-37. (in Chinese) doi: 10.3969/j.issn.1671-1637.2012.02.006 [8] 王辉, 沈钢. 磁悬浮车轨耦合振动的小比例相似模型[J]. 交通运输工程学报, 2014, 14(1): 49-56. doi: 10.3969/j.issn.1671-1637.2014.01.009WANG Hui, SHEN Gang. Small-scale similarity model of maglev-guideway coupling vibration[J]. Journal of Traffic and Transportation Engineering, 2014, 14(1): 49-56. (in Chinese) doi: 10.3969/j.issn.1671-1637.2014.01.009 [9] LI Jin-hui, LI Jie, ZHOU Dan-feng, et al. Self-excited vibration problems of maglev vehicle-bridge interaction system[J]. Journal of Central South University, 2014, 21(11): 4184-4192. doi: 10.1007/s11771-014-2414-5 [10] 何灼馀, 罗世辉, 梁海清. 低速磁浮列车二系悬挂动力学分析[J]. 交通运输工程学报, 2009, 9(1): 12-16. doi: 10.3321/j.issn:1671-1637.2009.01.003HE Zhuo-yu, LUO Shi-hui, LIANG Hai-qing. Dynamic analysis of secondary suspension for low-speed maglev train[J]. Journal of Traffic and Transportation Engineering, 2009, 9(1): 12-16. (in Chinese) doi: 10.3321/j.issn:1671-1637.2009.01.003 [11] ZHOU D F, HANSEN C H, LI J. Suppression of maglev vehicle-girder self-excited vibration using a virtual tuned mass damper[J]. Journal of Sound and Vibration, 2011, 330(5): 883-901. doi: 10.1016/j.jsv.2010.09.018 [12] 邹东升, 佘龙华, 张志强, 等. 磁浮系统车轨耦合振动分析[J]. 电子学报, 2010, 38(9): 2071-2075. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201009019.htmZOU Dong-sheng, SHE Long-hua, ZHANG Zhi-qiang, et al. Maglev vehicle and guideway coupling vibration analysis[J]. Acta Electronica Sinica, 2010, 38(9): 2071-2075. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXU201009019.htm [13] 王洪坡, 李杰. 一类非自治位置时滞反馈控制系统的亚谐共振响应[J]. 物理学报, 2007, 56(5): 2504-2516. doi: 10.3321/j.issn:1000-3290.2007.05.007WANG Hong-po, LI Jie. Sub-harmonic resonances of the non-autonomous system with delayed position feedback control[J]. Acta Physica Sinica, 2007, 56(5): 2504-2516. (in Chinese) doi: 10.3321/j.issn:1000-3290.2007.05.007 [14] ZHANG Ling-ling, HUANG Li-hong, ZHANG Zhi-zhou. Hopf bifurcation of the maglev time-delay feedback system via pseudo-oscillator analysis[J]. Mathematical and Computer Modelling, 2010, 52(5/6): 667-673. [15] POPP K. Mathematical modeling and control system design of maglev vehicles[D]. Hannover: Leibniz Universit?t Hannover, 1982. [16] 周又和, 武建军, 郑晓静, 等. 磁浮列车的动力稳定性分析与Lyapunov指数[J]. 力学学报, 2000, 32(1): 42-51. doi: 10.3321/j.issn:0459-1879.2000.01.005ZHOU You-he, WU Jian-jun, ZHENG Xiao-jing, et al. Analysis of dynamic stability for magnetic levitation vehicles by Lyapunov characteristic number[J]. Acta Mechanica Sinica, 2000, 32(1): 42-51. (in Chinese) doi: 10.3321/j.issn:0459-1879.2000.01.005 [17] 武建军, 郑晓静, 周又和. 弹性轨道上二自由度磁悬浮列车的动力特性分析[J]. 振动工程学报, 1999, 12(4): 439-446. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC199904000.htmWU Jian-jun, ZHENG Xiao-jing, ZHOU You-he. Dynamic characteristic analysis of maglev vehicle with two degrees of freedom on flexible guideways[J]. Journal of Vibration Engineering, 1999, 12(4): 439-446. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC199904000.htm [18] ZHENG Xiao-jing, WU Jian-jun, ZHOU You-he. Numerical analyses on dynamic control of five-degree-of-freedom maglev vehicle moving on flexible guideways[J]. Journal of Sound and Vibration, 2000, 235(1): 43-61. doi: 10.1006/jsvi.1999.2911 [19] 李云钢, 常文森. 磁浮列车悬浮系统的串级控制[J]. 自动化学报, 1999, 25(2): 247-251. https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO902.016.htmLI Yun-gang, CHANG Wen-sen. Cascade control of an EMS maglev vehicle's levitation control system[J]. Acta Automatica Sinica, 1999, 25(2): 247-251. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MOTO902.016.htm [20] 张东升, 梅雪松, 郝晓红, 等. 磁悬浮系统的电流控制方法[J]. 西安交通大学学报, 2007, 41(9): 1096-1100. doi: 10.3321/j.issn:0253-987x.2007.09.021ZHANG Dong-sheng, MEI Xue-song, HAO Xiao-hong, et al. Current control method for magnetic suspension system[J]. Journal of Xi'an Jiaotong University, 2007, 41(9): 1096-1100. (in Chinese) doi: 10.3321/j.issn:0253-987x.2007.09.021 -





 下载:
下载: