Importance measure of aircraft anti-icing cavity stucture parameters
-
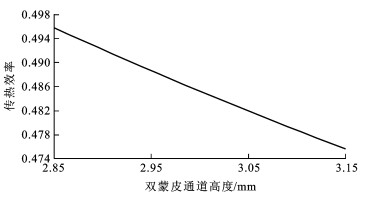
摘要: 分析了常见的3种飞机防冰腔结构, 应用Gambit软件建立了双蒙皮防冰腔结构网格模型。采用Spalart-Allmaras湍流模型模拟热气在防冰腔内的流动状况, 采用Fluent软件进行传热效率分析, 建立了防冰腔结构参数对传热效率的重要性测度模型。通过随机响应面法建立防冰腔结构参数与传热效率的函数关系, 采用低分散性抽样法求解防冰腔结构参数的重要性测度, 建立了防冰腔结构参数的重要性测度分析流程。分析结果表明: 当笛形管中心到外蒙皮的距离从35.15mm增加到38.85mm时, 传热系数由0.505减小到0.463;当双蒙皮通道高度从2.85mm增加到3.15mm时, 传热系数由0.495减小到0.476;当射流孔孔径从1.90mm增加到2.10mm时, 传热系数从0.505减小到0.494;当射流孔角度从14.25°增加到15.75°时, 传热系数从0.476增加到0.494。防冰腔结构参数的重要性排序依次为射流孔角度、笛形管中心到外蒙皮距离、射流孔孔径、双蒙皮通道高度, 在防冰腔结构加工与装配过程中, 需要重点考虑射流孔角度与笛形管中心到外蒙皮距离这2个参数。Abstract: The three common aircraft anti-icing cavity structures were analyzed, the grid model of anti-icing cavity structure with double skins was set up by using Gambit software. The flowing condition of heat in anti-icing cavity structure was simulated by using Spalart-Allmaras turbulence model, the heat transfer efficiency was analyzed with Fluent software, and the importance measure model of anti-icing cavity structure on heat transfer efficiency was built. The function relationship between structure parameters and heat transfer coefficient for anti-icing cavity was established by using the stochastic response surface method, the low dispersion sampling method was used to solve the importance measure, and the analysis process of importance measure for anti-icing cavity structure parameters was set up. Analysis result shows that when the distance between piccolo tube center and outer skin increases from 35.15 mm to 38.85 mm, the heat transfer coefficient reduces from 0. 505 to 0. 463. When the channel height of double skins increases from 2.85 mm to 3. 15 mm, the heat transfer coefficient reduces from 0. 495 to 0. 476. When the jet hole diameter increases from 1.90 mm to 2.10 mm, the heat transfer coefficient reduces from 0. 505 to 0. 494. When the jet hole angle increases from 14. 25~ to 15.75~, the heat transfer coefficient increases from 0. 476 to 0. 494. The importance order of anti-icing cavity parameters is the jet hole angle, the distance between piccolo tube center and outer skin, the jet hole diameter, the channel height of double skins. In the machining and assembly process of anti- icing cavity structure, the jet hole angle and the distance between piccolo tube center and outer skin are mainly considered.
-
0. 引言
民用飞机与运输机以亚音速穿越3000~8000m的云层,易发生结冰现象[1]。机翼积冰会增加飞机负重,改变飞机的气动外形,造成飞机的阻力增大,升力减小,导致稳定性和操纵性恶化,轻者引发飞行故障,重者会产生机毁人亡的惨剧[2-3],因此,为了保证民用飞机与运输机在结冰气象条件下的飞行安全,需要对飞机机翼等关键部位进行防除冰设计[4-5]。
现代化的飞机一般采用热防冰系统来防除冰,分为电热和热气2类。电热防冰是将电能转为热能而对部件表面加热来达到防除冰的目的[3],加热片嵌在飞机蒙皮内部,电加热片的热量通过导热对蒙皮外表面进行加热。热气防冰由发动机压气机引出的热空气经过引气系统到达机翼前缘,把热量传给蒙皮,使蒙皮表面达到一定的温度,保证表面不结冰或者融冰。相比于电热防冰,热气防冰系统的防除冰面积大,适合于机翼等大面积部位[6]。
防冰腔是机翼热气防冰系统的核心组成部件,性能好坏影响到飞机防除冰效率[7-8]。目前,结冰对飞机气动特性的影响与防冰系统性能预测等方面的研究比较多,防冰腔内部结构对飞机性能影响的研究相对较少[9-11]。管宁采用数值模拟方法对三维机翼表面的防冰热载荷进行分析,研究了完全蒸发防冰和不完全蒸发防冰中飞行条件和气象条件对防冰热载荷的影响[12];桑为民等分析了钝头型、尖头型和双角型3种不同冰型对翼型绕流及其气动特性的影响[13];周志宏等发展了1种结冰面沿法向网格线方向曲线增长的移动边界技术,对民机着陆构型的霜状冰进行了数值模拟[14];张强等基于6自由度方程对飞机的结冰飞行动力学问题进行了仿真研究,建立了结冰过程中飞机结冰严重程度与气动参数的计算方法[15];周玉洁采用数值模拟方法来优化防冰腔结构,基于参数对防护表面温度分布、防冰效率的影响来提高热气利用率[1];彭珑等采用计算流体力学方法对防冰腔内部热气流动与换热进行了模拟,得到了防冰腔热效率与热气喷射蒙皮内表面的对流传热系数的分布规律[16];卜雪琴等利用热流体系统仿真分析平台Flowmaster软件和计算流体力学Fluent软件进行联合仿真,通过研究笛形管热气喷口孔径、孔数与孔间距等参数对防冰系统进行设计和性能分析[17]。需要指出的是,上述研究大多基于确定性分析,忽略了由于制造、装配等环节不确定因素导致防冰腔结构尺寸的参数具有随机不确定性。结构参数的分散性导致传热效率也存在分散性,传热效率的波动影响到机翼的防除冰效果[18-20]。
本文以飞机直喷式双蒙皮防冰腔结构为研究对象,通过Fluent软件对防冰腔进行仿真分析,得到传热效率,建立针对传热效率的结构参数重要性测度模型,采用随机响应面法得到显式的函数表达式,基于低分散性抽样进行参数的重要性测度分析。
1. 防冰腔结构参数重要性测度建模
1.1 直喷式双蒙皮防冰腔结构
热气防冰腔有直喷式防冰腔、直喷式双蒙皮防冰腔和微引射式防冰腔3种常见的结构形式。直喷式防冰腔结构设计简单,加工方便,但后腔蒙皮温度换热较差。相比于直喷式防冰腔,直喷式双蒙皮防冰腔在防冰腔后腔多加了1层蒙皮,改善了后腔防冰区域的换热情况。微引射式防冰腔也在后腔采用了双蒙皮设计,但需要较大的入口动压通过双蒙皮通道,这会导致热气损失较大,且微引射器的加工与安装比较困难,目前的热气防冰系统多采用直喷式双蒙皮结构[6]。本文以某型直喷式双蒙皮防冰腔结构为例开展研究,防冰腔、双蒙皮和笛形管结构分别见图 1~3,蒙皮厚度为1.5 mm,笛形管直径为40mm,射流孔间距为25mm。
在机翼前缘的防除冰过程中,发动机引气系统引来热气经管路到达机翼前缘缝翼内的笛形管中,从笛形管上的射流孔喷射在前腔内表面上,加热蒙皮,热气经过双蒙皮通道流向后腔,最后从后腔的排气口排出。
1.2 防冰腔结构传热效率分析
借助Gambit软件对防冰腔结构进行网格划分,结果见图 4。为增加计算精度,在射流孔出口附近对网格进行加密处理,见图 5。
由于防冰腔内为射流孔高速喷出的热气,热气在防冰腔内流动,受腔内结构与热气速度的影响,流动形式为湍流。为准确模拟热气在防冰腔内的流动,采用Spalart-Allmaras(S-A)湍流模型进行仿真计算。
在S-A湍流模型中,边界条件设置为:将射流孔处设置为压力入口,射流孔处压力为0.2MPa,热气温度为473.15K;出口处设置为与环境压力相同的压力出口,外部环境温度设置为263.15K;两侧挡板设为对称边界;防冰腔蒙皮外壁面设为对流壁面,对流换热系数反映外流场来流速度。详细边界条件类型见表 1。
表 1 边界条件类型Table 1. Types of boundary conditions
应用Fluent软件进行腔内流动与换热模拟,根据能量方程仿真计算采用S-A湍流模型,离散格式采用二阶迎风格式,仿真迭代达到约5000步后收敛,通过Fluent软件计算得到机翼外蒙皮表面温度分布见图 6,从中可看出在前缘驻点附近外蒙皮温度达到最高值,外蒙皮温度沿弦向递减,在防冰腔下表面末端达到最低值。
根据文献[6],定义防冰腔结构传热效率η为加热机翼表面的热气能量占系统所提供热气能量的比例为

式中:T1、T2、T3分别为防冰腔入口热气温度、出口热气温度与防冰区域外蒙皮平均温度。
通过Fluent软件模拟分析计算,得到防冰腔结构传热效率为48.527%。过低的传热效率会增大发动机用于防除冰的引气量,不仅造成燃油浪费,而且增加了发动机的负载,影响其性能,因此,传热效率是评价防冰腔性能优劣的一个重要指标。
1.3 结构参数重要性测度模型
由于制造、装配等因素带来的影响,导致防冰腔结构参数具有分散性,可以处理为随机变量,这些变量相互独立。根据目前的加工工艺和工程经验,得到结构参数的分布类型和相关参数见表 2。如果变量之间存在相关性时,可通过Nataf变换将相关变量转化为相互独立的变量[21]。
表 2 参数的分布类型Table 2. Distribution types of parameters
假定变量xk(k=1~4)的概率密度函数为f(xk),结构参数的联合概率密度为

(1) 评估防冰腔结构设计的好坏,能否达到预定的功能,重点在于考核结构的传热效率η。xk均为随机变量导致η也是随机变量,而且是xk的隐函数。
重要性测度分析是结构设计的一项重要工作,能甄别影响结构性能的关键参数,从而指导结构改进设计。根据文献[18-19],可定义防冰腔结构参数xk对η的重要性测度Sk为

(2) 式中:V(η)为η的方差;E(η|xk)为在xk作用下η的均值。
通过式(1)抽取参数xk的N个样本,则V(η)的估计值V(η)可表示为

(3) 式中:xk,j为通过式(1)抽取的N个样本中的第j个样本;η(xk,j)为xk,j对应的传热效率。
通过式(1)抽取参数xk的N1个样本,对于第p(p≤N1)个样本xk,p,以剩余的3个概率密度函数组成的条件概率从N1中抽取M个样本,则E(η|xk,p)的估计值E(η|xk,p)可写为

(4) 式中:xk,p,j′为通过式(1)抽取的M个样本中的第j ′个样本;η(xk,p,j′)为xk,p,j′对应的传热效率。
V[E(η|xk)]的估计值V[E(η|xk)]可表示为

(5) 将式(3)、(5)代入式(2)即可求解得到Sk的估计值Sk。结构参数xk的重要性测度指标Sk表征了在参数xk单独作用下的不确定性对结构传热效率η的变异性的影响程度,这种基于方差的重要性测度能从方差的角度反映结构参数对传热效率变异性的影响,从而为调整设计值的分布参数以控制结构传热效率变异性提供依据和指导。
2. 防冰腔结构参数重要性测度求解
在进行防冰腔结构参数的重要性测度分析过程中,通过随机响应面和低分散性抽样相结合的方法,来解决结构参数重要性测度计算量大、收敛慢的问题。
由于结构传热效率η是参数xk的隐函数,需要借助Fluent软件分析才能得到相应的响应值。由式(2)可以看出,进行重要性测度分析需多次调用Fluent软件进行传热效率η的分析计算,计算量很大,因此,在进行结构参数的重要性测度分析时,首先需要借助高精度的拟合方法对传热效率η进行拟合,将隐函数显式化。响应面法通过一系列确定性的“试验”拟合一个响应面来模拟真实极限状态曲面,在航空航天结构、岩土边坡等领域的可靠性分析上应用广泛[22]。相比于传统响应面法,随机响应面法拥有特殊的样本点选取方式,并采用Hermite多项式来拟合功能函数的表达式,不需要迭代计算,可以较大程度减少计算量[23-24]。本文采用随机响应面方法解决防冰腔结构传热效率η的隐函数显式化问题,最终得到η的拟合值

2.1 传热效率基于随机响应面的拟合
进行随机响应面法分析的第1步是将结构参数xk进行标准正态化处理。设标准正态变量为ξk,其转换式为

(6) 式中:μk、σk分别为结构参数xk的均值和标准差。
采用Hermite随机多项式展开η,得到


(7) 式中:ξk1 ~ξk4均为三阶Hermite多项式的根;a0、ak1、ak2,k2、ak3,k4均为待定系数。
将式(7)中的待定系数组成矩阵A,可以通过最小二乘法求解A。
ξk1~ξk4均为三阶Hermite多项式的根,取均值可能为0


(8) 式中:B为由30个试验样本构成的30×15矩阵;V为30个试验样本对应的真实响应值构成的30×1列阵。
求出待定系数矩阵A,即可获得二阶显式的随机响应面函数

2.2 基于低分散性抽样的结构参数重要测度分析
低分散性抽样是采用数论方法排除随机性,能具体、确切地给出高度均匀分布的样本点。常见的低分散性抽样可以基于好格子点集、好点集、最佳一致点集等3种点集。在这3种点集中,好格子点集和最佳一致点集是一个有限集,对抽样数进行了强行规定,不能在已有抽样信息的基础上追加样本,这会浪费已有的抽样信息[26]。当采用数字模拟方法进行参数的重要性测度分析时,所需的抽样数并不能预先得知,这制约了好格子点集和最佳一致点集在防冰腔结构参数重要性测度中的应用。好点集没有该方面的缺点,因此,本文的低分散性样本基于好点集的基本思路进行。
以前文的xp,k为例,先产生1对好点(rk,p,1,rk,p,2),构造式为

(9) 
(10) 
(11) 式中:int(·)为取整运算符号;s为质数,且s≥19。
3. 重要性测度分析
在结构参数均值点附近,分析笛形管中心到外蒙皮距离、双蒙皮通道高度、射流孔孔径与射流孔角度对传热效率(系数)的影响,其变化规律分别见图 7~10。
图 7~10反映了笛形管中心到外蒙皮距离、双蒙皮通道高度、射流孔孔径与射流孔角度等参数在均值点附近的波动对结构传热系统存在一定的影响,但这种分析是局部的,未能从全局的角度反映结构参数波动对传热系统的影响。根据前文的分析,可以得到防冰腔结构参数重要性测度分析的流程,见图 11,防冰腔结构参数的重要性测度分析结果见图 12。在防冰腔结构的4个参数中,笛形管中心到外蒙皮距离和射流孔角度这2个参数的重要性测度值较大,说明这2个参数对防除冰传热效率有较大影响。
4. 结语
针对防冰腔结构参数的重要性测度模型,本文给出了基于随机响应面和低分散性抽样相结合的求解方法,解决防冰腔结构参数重要性测度分析计算量大、收敛慢的问题。通过重要性测度分析,发现笛形管中心到外蒙皮的距离和射流孔角度2个参数的波动对防冰腔传热效率有较大影响,因此,在防冰腔结构优化设计、加工与装配等过程中需要重点关注这2个参数。本文虽然针对飞机防冰腔结构参数进行重要性测度分析,但需要指出的是,本文的分析仅针对于结构传热效率这一评价指标,有待继续深入研究针对多个指标综合评估的重要性测度。
-
表 1 边界条件类型
Table 1. Types of boundary conditions

表 2 参数的分布类型
Table 2. Distribution types of parameters

-
[1] 周玉洁. 热气腔结构的优化设计与数值模拟[D]. 南京: 南京航空航天大学, 2010.ZHOU Yu-jie. Optimal design and numerical simulation of the hot air cavity structure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010. (in Chinese) [2] THOMAS S K, CASSONI R P. Aircraft anti-icing and de-icing techniques and modeling[J]. Journal of Aircraft, 1996, 33(5): 841-854. doi: 10.2514/3.47027 [3] 李航航, 周敏. 飞机结冰探测技术及防除冰系统工程应用[J]. 航空工程进展, 2010, 1(2): 112-115. doi: 10.3969/j.issn.1674-8190.2010.02.004LI Hang-hang, ZHOU Min. Engineering application of icing detection technique and anti-icing and deicing system on aircraft[J]. Advances in Aeronautical Science and Engineering, 2010, 1(2): 112-115. (in Chinese) doi: 10.3969/j.issn.1674-8190.2010.02.004 [4] 卜雪琴, 郁嘉, 林贵平, 等. 机翼气热防冰系统设计[J]. 北京航空航天大学学报, 2010, 36(8): 927-930.BU Xue-qin, YU Jia, LIN Gui-ping, et al. Investigation of the design of wing hot-air anti-icing system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8): 927-930. (in Chinese) [5] 常士楠, 袁美名, 霍西桓, 等. 某型飞机机翼防冰系统计算分析[J]. 航空动力学报, 2008, 23(6): 1141-1145. https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200806031.htmCHANG Shi-nan, YUAN Mei-ming, HUO Xi-heng, et al. Investigations of the bleed air anti-icing system for an aircraft wing[J]. Journal of Aerospace Power, 2008, 23(6): 1141-1145. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200806031.htm [6] 姚会举. 机翼热气防冰腔功能可靠性分析及优化设计[D]. 西安: 西北工业大学, 2014.YAO Hui-ju. Function reliability analysis and optimal design of the wing hot-air anti-icing cavity[D]. Xi'an: Northwestern Polytechnical University, 2014. (in Chinese) [7] SILVA G A L, SILVARES O M, ZERBINI E J G J. Numerical simulation of airfoil thermal anti-ice operation, part 1: mathematical modeling[J]. Journal of Aircraft, 2007, 44(2): 627 -634. doi: 10.2514/1.544 [8] LIU H H T, HUA Jun. Three-dimensional integrated thermodynamic simulation for wing anti-icing system[J]. Journal of Aircraft, 2004, 41(6): 1291-1297. doi: 10.2514/1.5594 [9] MORENCY F, TEZOK F, PARASCHIVOIU I. Heat and mass transfer in the case of anti-icing system simulation[J]. Journal of Aircraft, 2000, 37(2): 245-252. doi: 10.2514/2.2613 [10] BROWN J M, RAGHUNATHAN S, WATTERSON J K. Heat transfer correlation for anti-icing system[J]. Journal of Aircraft, 2003, 40(1): 65-70. [11] 杜雁霞, 桂业伟, 肖春华, 等. 飞机结冰过程的传热研究[J]. 工程热物理学报, 2009, 30(11): 1923-1925. doi: 10.3321/j.issn:0253-231X.2009.11.034DU Yan-xia, GUI Ye-wei, XIAO Chun-hua, et al. Investigation of heat transfer in aircraft icing[J]. Journal of Engineering Thermophysics, 2009, 30(11): 1923-1925. (in Chinese) doi: 10.3321/j.issn:0253-231X.2009.11.034 [12] 管宁. 三维机翼防冰热载荷的数值模拟[D]. 南京: 南京航空航天大学, 2007.GUAN Ning. Numerical simulation of anti-icing thermal loads on a 3d airfoil[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. (in Chinese) [13] 桑为民, 蒋胜矩, 李凤蔚. 翼型冰增长和结冰影响的数值模拟研究[J]. 应用力学学报, 2008, 25(3): 371-375. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200803006.htmSANG Wei-min, JIANG Sheng-ju, LI Feng-wei. Numerical simulation for ice accretion and icing effects on airfoils[J]. Chinese Journal of Applied Mechanics, 2008, 25(3): 371-375. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX200803006.htm [14] 周志宏, 易贤, 桂业伟, 等. 复杂3维外形霜状冰数值模拟[J]. 四川大学学报: 工程科学版, 2012, 44(增2): 158-162. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH2012S2039.htmZHOU Zhi-hong, YI Xian, GUI Ye-wei, et al. Prediction of rime ice accretion on complex configurations[J]. Journal of Sichuan University: Engineering Science Edition, 2012, 44(S2): 158-162. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH2012S2039.htm [15] 张强, 高正红. 基于六自由度方程的飞机结冰问题仿真[J]. 飞行力学, 2013, 31(1): 1-4. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201301000.htmZHANG Qiang, GAO Zheng-hong. Simulation of ice accretion based on six degree-of-freedom equation[J]. Flight Dynamics, 2013, 31(1): 1-4. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX201301000.htm [16] 彭珑, 卜雪琴, 林贵平, 等. 热气防冰腔结构参数对其热性能影响研究[J]. 空气动力学学报, 2014, 32(6): 848-853. https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201406019.htmPENG Long, BU Xue-qin, LIN Gui-ping, et al. Influence of the structural parameters on thermal performance of the hot air anti-icing system[J]. Acta Aerodynamica Sinica, 2014, 32(6): 848-853. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201406019.htm [17] 卜雪琴, 林贵平, 郁嘉. 三维内外热耦合计算热气防冰系统表面温度[J]. 航空动力学报, 2009, 24(11): 2495-2500. https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200911015.htmBU Xue-qin, LIN Gui-ping, YU Jia. Three-dimensional conjugate heat transfer simulation for the surface temperature of wing hot-air anti-icing system[J]. Journal of Aerospace Power, 2009, 24(11): 2495-2500. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKDI200911015.htm [18] SALTELLI A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579-590. doi: 10.1111/0272-4332.00040 [19] BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering and System Safety, 2007, 92(6): 771-784. doi: 10.1016/j.ress.2006.04.015 [20] WANG Pan, LU Zhen-zhou, TANG Zhang-chun. Importance measure analysis with epistemic uncertainty and its moving least square solution[J]. Computers and Mathematics with Applications, 2013, 66(4): 460-471. doi: 10.1016/j.camwa.2013.06.001 [21] LI Hong-shuang, LU Zhen-zhou, YUAN Xiu-kai. Nataf transformation based point estimate method[J]. Chinese Science Bulletin, 2008, 53(17): 2586-2592. [22] 李炜. 边坡稳定性联合评价方法[J]. 交通运输工程学报, 2010, 10(5): 8-11. doi: 10.3969/j.issn.1671-1637.2010.05.002LI Wei. Combined evaluation method of slope stability[J]. Journal of Traffic and Transportation Engineering, 2010, 10(5): 8-11. (in Chinese) doi: 10.3969/j.issn.1671-1637.2010.05.002 [23] LIU Ying. Application of stochastic response surface method in the structural reliability[J]. Procedia Engineering, 2012, 28: 661-664. doi: 10.1016/j.proeng.2012.01.787 [24] KAYMAZ I, MCMAHON C A. A response surface method based on weighted regression for structural reliability analysis[J]. Probabilistic Engineering Mechanic, 2005, 20(1): 11-17. doi: 10.1016/j.probengmech.2004.05.005 [25] 汪新槐. 多维数值积分的数论方法及其在结构可靠度分析中的应用[D]. 南京: 河海大学, 2005.WANG Xin-huai. Number theoretical method for numerical multiple integrals and the application in structural reliability analysis[D]. Nanjing: Hohai University, 2005. (in Chinese) [26] DAI Hong-zhe, WANG Wei. Application of low-discrepancy sampling method in structural reliability analysis[J]. Structural Safety, 2009, 31(1): 55-64. doi: 10.1016/j.strusafe.2008.03.001 [27] 戴鸿哲, 王伟. 结构可靠性灵敏度分析的低偏差抽样方法[J]. 工程力学, 2010, 27(1): 104-108. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201001021.htmDAI Hong-zhe, WANG Wei. Low discrepancy sampling method for structural reliability sensitivity analysis[J]. Engineering Mechanics, 2010, 27(1): 104-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201001021.htm -






 下载:
下载:












 下载:
下载: