Commute activity identification based on spatial and temporal information of transit chaining breaks
-
摘要: 分析了公交智能卡数据挖掘中转乘行为、通勤出行、非通勤出行识别的改进方法, 将关注点从公交换乘过程信息转移到换乘链间隔期的持续时长和空间位移信息, 以换乘链断裂时长和位移2个维度计算公交换乘链断裂点概率, 制作工作日和非工作日断裂点时空变量联合概率分布矩阵, 对比了这2种分布的差异;检验了断裂时长序列和断裂位移序列的稳定性, 标识了2条曲线的突变点和拐点, 用于推断转乘引起的转移距离和转乘时长的阈值参数;对工作日和非工作日差值时长序列曲线进行移动平均滤波处理, 使得曲线的突变与极值之间的关联能够解释转乘、通勤出行和非通勤出行3种行为与通勤和非通勤出行之间的关联;采用北京市整个一周的地面公交和地铁系统样本数据对方法进行验证, 并根据时间序列和位移序列曲线确定样本数据中常见公交换乘行为的阈值参数。分析结果表明:断裂点时空信息对样本数据中的换乘行为能提供更合理的识别分类参数;持卡人在站点间转移的容忍距离约为1.6km;断裂点转乘时长与非通勤出行的断裂时长临界点为22~48min;非通勤出行和通勤出行的时长临界点约为478min, 非通勤出行断裂点最大概率时长为140min;通勤出行的断裂时长接近期望值为601且标准差为44的正态分布;基于新方法得出的参数改善了公交出行活动的识别率, 转乘行为、通勤出行与非通勤出行的识别率分别提高了16.1%、4.2%、6.2%。可见, 换乘链断裂点的时间信息和空间信息不但可作为公交换乘行为识别的依据, 还可能带来更好的识别效果。Abstract: An approach to improve the recognition of transfers, working commutes, and nonworking commutes in smartcard data mining was introduced.The study focus was shifted from the information of transit processes to the durations and displacements between the transit chaining breaks.The probabilities of transit chaining breaks were calculated by two dimensions of the break durations and displacements, and a joint probability distribution matrix of spatial andtemporal variables for workdays and non-working days was made.The differences between the two types of distribution were compared.The stabilities of the break duration sequences and break displacement sequences were examined.The mutation points and turning points of the two curves were marked to infer the important threshold parameters for the transferring durations and displacements generated by the transfers.A moving average filter was utilized to smooth both workdays and non-working days curves of margin duration values.The relationship between the mutation and extremes of the curve was explained for the three types of commute activities relating to the transfers, working commutes, and non-working commutes.The approach was verified by a weeklong sample dataset of the Beijing bus and subway system.The threshold parameters of the common commute activities in the dataset were determined according to the time series and the displacement sequence curve.Analysis result shows that the spatial and temporal information at the breaks can provide more reasonable identification parameters for the commute activities.A tolerance distance of approximately 1.6 km between the transit connections is found among the cardholders.The threshold of transit break duration between the transferring and non-working commutes is 22-48 min.The threshold of working and non-working commutes is approximately 478 min, and the maximum probability of non-working duration is 140 min.The transit chaining break durations of working commutes fall into a normal distribution with an expected value of 601 and a standard deviation of 44.The parameters generated by the new approach lead to an improvement in commute activity recognition, the recognition rates of the transfers, working commutes and non-working commutes increse by 16.1%, 4.2%and 6.2%, respectively.So the spatial and temporal information of transit chaining breaks can not only provide the basis for the commute activity identification, but also achieve better recognition results.
-
0. 引言
智能卡在城市公共交通的应用日益普及, 带有时间印戳和地理标签的海量刷卡数据为换乘行为模式研究提供了条件[1,2,3,4,5,6]。识别转乘行为对推导出行起讫地、优化公交系统、降低转乘延误具有重要意义[2,3,6], 而识别通勤换乘行为对预测城市区域间运力需求, 缓解高峰时段拥堵, 提升公共交通服务水平非常重要[1,2,4]。人的空间行为与交通系统相互影响[7,8,9], 基于出行行为与交通系统紧密的关联, 交通工程师和地理学者开展了大量公共交通换乘行为识别的相关研究[10,11,12]。
Bagchi等进行了换乘链研究, 并使用30min之内紧接的换乘作为转乘行为判据[13];吴祥国对有转乘和无转乘行为进行分类, 推导站点间OD矩阵[14];Alsger等在研究转乘行为时不仅考虑了转乘行为时长, 还结合徒步容忍距离分析转乘行为[15];Ali等使用30min时长极限判断单次换乘的结束点是否为出行目的地[16]。这些转乘相关研究使用的参数与所在城市实际调研较为一致, 但参数确认方法适普性有限, 缺少对特定公交系统的个性化统计分析。公共交通服务时长等参数受多种因素影响, 比如在公交站点布局不合理或共享单车大量使用的交通情况下, 站点间转移容忍距离和转移速度会有所提升, 换乘行为识别参数选择方法需要对新交通环境具有适应性[17,18,19]。
通勤换乘研究方面:Agard等采用工作日上车行为发生时间补全出行表, 用聚类法对通勤人群进行了分类[20];Pelletier等认为换乘行为建模是公交数据研究的首要问题[5];龙瀛等通过识别通勤行为开展了职住分离研究[21];Tao等认为刷卡数据是反映出行人的时空信息, 并注意到成年人 (工作人群) 与其他群体的出行时空差异[22];Cho等基于对居住和商用区之间换乘进行建模预测交通需求[23]。这些聚焦通勤出行的研究促进了人们对城市交通供需空间不均衡的认识, 但多数研究将早晚高峰出行时间作为识别通勤换乘的主要依据, 参数选择过程缺少对个体与群体换乘行为时间数据和空间数据的统计分析。现有通勤换乘研究大多未考虑地面公交和地铁 (城市轨道) 接驳之间的出行行为[4,5], 组合使用公交和地铁上下班的通勤难免被统计成2个个体的通勤, 且在2种交通方式接驳的转乘点会被错误统计成出行目的地[24,25,26]。
总体而言, 现有研究过多关注公交换乘本身, 对换乘中断的空白期重视不足。本文视角从公交换乘过程切换到换乘间断的空白期, 将研究重心从公交服务的单次换乘旅行时长和单次换乘旅行距离转向换乘断裂点持续时间 (断裂时长) 和空间错位 (断裂位移) , 提出基于断裂点时空信息的公交换乘行为识别分类方法 (断裂点分析法) ;将地面公交和地铁换乘平等对待, 同时纳入换乘链, 充分利用断裂点时空信息, 识别转乘、通勤换乘和非通勤换乘3种行为的时长和位移参数边界。
1. 换乘链断裂点时空信息
1.1 换乘链断裂时长与断裂位移
与出行链研究不同, 本文仅讨论地铁和地面公交2种集约出行方式, 不关注其他机动化出行方式。文中的换乘 (Transit) 和转乘 (Transfer) 没有包含关系, 前者是单次公交和地铁出行, 后者从地面公交或地铁线路转移到另外一个公共交通线路。公共交通出行链在本文中简称为换乘链。公交刷卡数据通常以单次换乘结构化存储, 反映持卡人进入公交系统 (包括地面公交和轨道交通, 但不含地铁内部的转乘) 至刷卡离开的过程, 而本文换乘链数据库是对单次换乘按单人日志的数据重构。这个重构过程对于地面公交刷卡和地铁刷卡是平等对待的。
换乘链断裂点 (Transit Chaining Break, TCB) 指某次换乘与紧接的下一次换乘之间的空白期, 其时空属性与2个关键变量相关, 其中断裂时长T (TCB Duration) 为某次刷卡记录结束到紧接的下一次刷卡记录开始之间的时间;断裂位移S (TCB Displacement) 为某次出站站点与紧接的下一次进站站点间的直线距离。
如一个持卡人单日共4次换乘, 其时间排序则为换乘链:07:30 (公交A站) →07:55 (公交B站) ;08:05 (地铁C站) →08:46 (地铁D站) ;17:37 (公交E站) →17:59 (公交F站) ;18:12 (公交F站) →19:01 (公交G站) 。
若B站与C站距离为300m, D站和E站距离为400m, 那么第1个断裂点在B站和C站之间, T=10min, S=300m, 第2个断裂点在D站和E站之间, T=531 min, S=400 m, 第3个均在F站, T=13min, S=0m。该换乘链刻画了一个人2次转乘的通勤往返行为。
1.2 断裂点时空信息的T-S矩阵
T-S矩阵是用于确认断裂点T和S关系。由于换乘行为在总量中的占比可能具有稳定性, 使用P (T) 和P (S) 代表2个维度中断裂点的概率, P (T, S) 代表二维矩阵中的概率。S以距离s为尺度划分切片区间[0, s]、 (s, 2s]、 (2s, 3s]、…、 ((m-1) s, ms], T以时间t为尺度划分切片区间 (0, t]、 (t, 2t]、 (2t, 3t]、…、 ((n-1) t, nt], 其中m和n分别为空间和时间维度切片的次序。m切片和n切片对应断裂点的概率构成的T-S矩阵A为

式中:amn为符合S∈ ((m-1) s, ms]且T∈ ((n-1) t, nt]条件的断裂点占比。
矩阵中坐标反映了断裂点T和S的关系, 在一个断裂时长里, 持卡人行为包括但不限于:在原地等待、就近移动到其他地点进入公交系统、离开原站点但完成出行目的后又返回到该地点重新进入公交系统。断裂点T和S这2个变量是一个有逻辑的组合。工作日和非工作日的T-S矩阵分布可能会因上下班通勤表现出差异, 而转乘行为更多地受公交网络组织运营影响, 在工作日和非工作日的T-S矩阵中不会表现太大差异。
1.3 T序列和S序列
T序列是每个T切片向量 (P (T1) , P (T2) , P (T3) , …, P (Tn) ) , 其中P (T1) ~P (Tn) 为第1~n个T切片对应断裂点概率。在n×m的T-S矩阵中也可用m维的行向量 (1, 1, 1, …, 1) 乘矩阵A计算。同样可以得到S序列 (P (S1) , P (S2) , P (S3) , …, P (Sm) ) , 其中P (S1) ~P (Sm) 为第1~m个S切片的概率, 也可通过n×m的T-S矩阵中用n维行向量 (1, 1, 1, …, 1) 乘AT得到。2个序列用于单一时间维度或空间维度的分析。T序列的稳定性评价采用T序列评价指标Hx, y表示为

式中: (P (T1) , P (T2) , P (T3) , …, P (Tn) ) x为编号为x的P (T1) ~P (Tn) 共n个切片概率所组成的向量; (P (T1) , P (T2) , P (T3) , …, P (Tn) ) y为编号为y的P (T1) ~P (Tn) 共n个切片概率所组成的向量。
S序列的稳定性评价采用S序列评价指标Kx, y表示为

式中: (P (S1) , P (S2) , P (S3) , …, P (Sm) ) x为编号为x的P (S1) ~P (Sm) 共m个切片概率所组成的向量; (P (S1) , P (S2) , P (S3) , …, P (Sm) ) y为编号为y的P (S1) ~P (Sm) 共m个切片概率所组成的向量。
由于序列为概率值, Hx, y和Kx, y若为0则代表2个序列重叠, 1代表完全不同, 2个评价指标均在[0, 1]区间, 值的大小代表序列的稳定性, 越接近1, 稳定性越强, 认为其特征值越适用于行为识别。
公交系统中, 持卡人离开公交系统及再次进入公交系统的时长T与换乘行为直接关联, 转乘T可能较短, 就业对应的T可能会与8h工作制相一致, 而购物之类的换乘出行可能表现为比就业通勤较短的T。持卡人离开公交系统, 再次进入站点的空间错位S也与出行行为相关, 转乘行为持卡人一般寻求最短的机会再次进入, 而通勤持卡人一般会原地或就近选择返家的站点。对公交系统依赖低的群体, 站点间采用出租车等机动化交通工具, 产生的S则会较大。所以, T序列和S序列的曲线突变点、极值、拐点与换乘行为是有关联的。
序列中干扰整体分析的噪声信号, 使用移动平均滤波器 (Moving Average Filter, MAF) 平滑处理, 处理后的平滑序列向量中第n个T变量Tn为

式中:P (Ti-l) ~P (Ti+l) 分别为移动平均滤波时使用的共2l+1个切片对应的概率, i为处理点对应的序号, l为跨越序号i的步长。
若l取10min, 即对±10min的曲线范围进行平滑处理, 而10min在公共交通出行的时间分析中不会影响曲线的整体趋势。
2. 断裂点分析方法的步骤
2.1 断裂点时空信息的作用与处理方法
为了方便研究, 针对不同的换乘行为对T和S产生的影响, 处理过程使用了不同分辨率的断裂点时间和空间数据。低精度T-S矩阵用于了解不同换乘行为在工作日和非工作日的分布, 粗略确认转乘行为、通勤出行行为和非通勤出行行为的时空范围;高精度T-S矩阵用于检验非机动化转乘行为;T序列和S序列用于较精确地分析转乘行为时长阈值和持卡人在站点间非机动化转移的容忍距离;工作日和非工作日差值序列用于确认通勤出行与非通勤出行的时长阈值。通过分析和处理换乘链断裂点时空信息, 得到换乘行为分析的识别参数或分类结果, 表1为换乘链断裂点时空信息的数据类型、在换乘行为识别中的作用以及对应的处理方法。
表 1 换乘链断裂点时空信息分类Table 1. Classification of TCB spatial and temporal information
2.2 断裂点时空信息阈值确认原则
根据上文所述, 本文主要使用T序列和S序列分析获得转乘时长阈值、非机动化转移容忍距离、通勤出行时长和非通勤出行的时长边界、通勤出行与非通勤出行时长众数。阈值确认时, 断裂点时空信息聚类与换乘行为分类相关, 概率曲线的极值与行为概率最大值相关, 概率曲线的突变点与行为的界限相关。
确认规则为:转乘时长阈值由通过检验的T序列曲线在合理转乘时长附近的突变点确认, 一般选择 (0, 1) h作为突变点, 观察范围不会出现太大偏差, 毕竟换乘平均超过60min的城市是很少的;非机动化转移容忍距离由S序列反映的同站点转乘和邻近站点转移距离确定, 大型城市市区的公交站点布局紧密, 持卡人一般不会选择多于1站地的站点再次上车;通勤出行时长和非通勤出行的时长边界是工作日与非工作日的差值T序列为0时的坐标, 在这个时长点 (通常小于8h) , 工作日的统计量不超过非工作日, 通勤出行失去主导地位;通勤出行时长众数是工作日与非工作日的差值T序列最大值坐标, 这个时长是工作日多出的通勤产生的波峰 (一般大于8h) ;非通勤出行时长众数是工作日与非工作日的差值T序列最小值坐标, 在这个时长点 (一般为1~8h) , 非工作日的统计量占主导。
2.3 阈值参数与换乘行为分类
转乘行为T小于转乘时长阈值且S小于非机动化转移容忍距离的断裂点;通勤出行是S小于非机动化转移容忍距离且T时长大于通勤出行时长和非通勤出行的时长边界的断裂点;非通勤出行是S小于非机动化转移容忍距离且T在转乘时长阈值与通勤出行时长边界的断裂点;S大于非机动化转移容忍距离的断裂点持卡人借助了其他机动化交通方式, 表现出对公交系统的低依赖度;持卡人借助了公共交通之外其他快速工具或数据错误在S/T大于极限速度的断裂点, 极限速度可能包括步行或低速骑行。
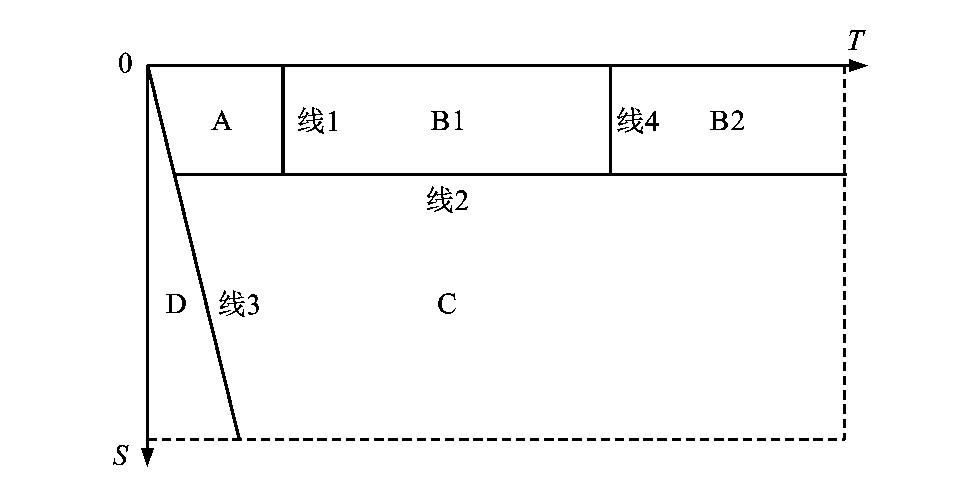
换乘行为分类与识别出的断裂点时空阈值相关, 见图1, 可见:线1表示合理转乘时间阈值, 线2代表非机动化转移容忍距离, 线3的斜率绝对值为非机动化转移速度的极限, 线4代表就业通勤与非通勤出行的时长阈值, 则A类断裂点可对应转乘行为, B1类断裂点为通勤出行, 可对应为通勤出行行为, B2类对应非通勤出行行为, C类对应对公共交通网络依赖度较低的换乘行为, D类代表非合理转乘或数据异常。
3. 试验结果分析
3.1 数据描述
试验样本主要选择北京市交通信息中心2016年8月7~13日连续一周的一卡通刷卡数据。样本包含地面公交和地铁2种公共交通方式中所有卡号换乘记录 (约1.4×108条) , 每条记录包含了换乘起始点空间信息 (上下车站点) 和时间信息 (上下车时间) 。以星期三为例, 共有换乘链4 872 420条, 断裂点9 960 127个, 而在星期日共有换乘链3 543 078条, 断裂点6 883 165个。
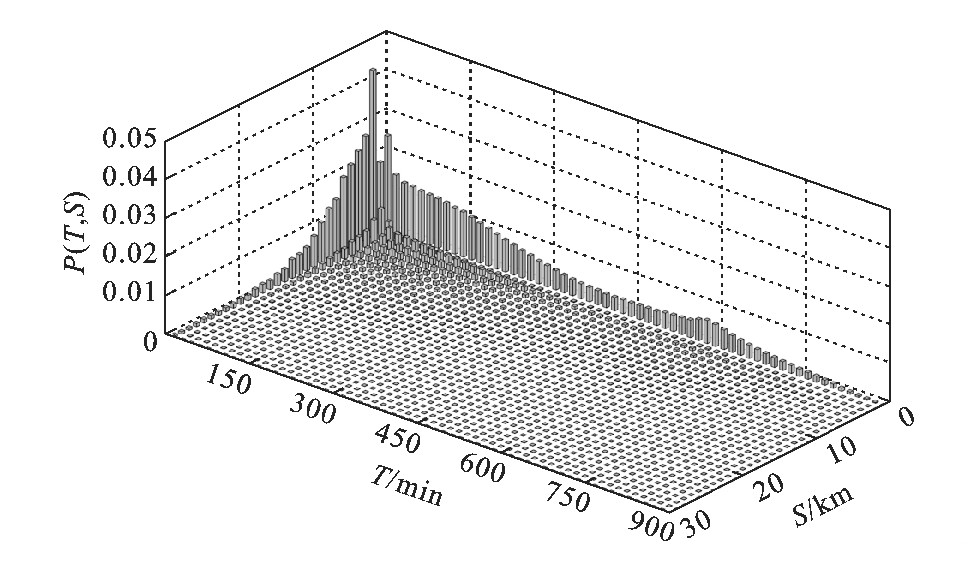
使用t=15min, s=0.5km作为切片参数, 制作T∈ (0, 900]min, S∈[0, 3]km工作日和非工作日T-S矩阵, 分别见图2、3, 得出如下结论:2个矩阵有共同特征, 在T<30min且S<2km处呈现大量断裂点, 在T>30min和S>2km时断裂点较少;2个矩阵也存在差异, S<2km范围内, T∈ (30, 500) min时工作日断裂点少于非工作日, T>500min时工作日断裂点多于非工作日。
3.2 T和S稳定可用性检验
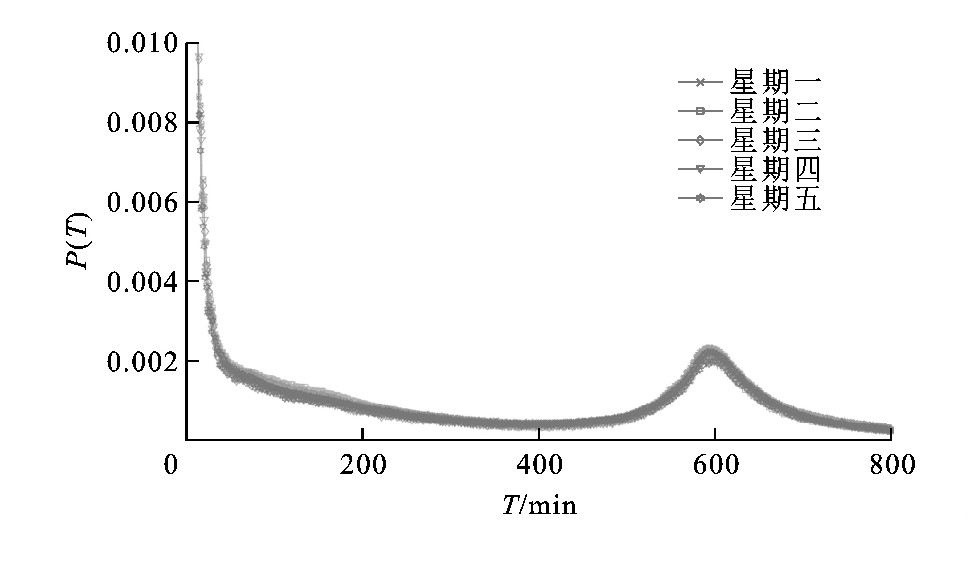
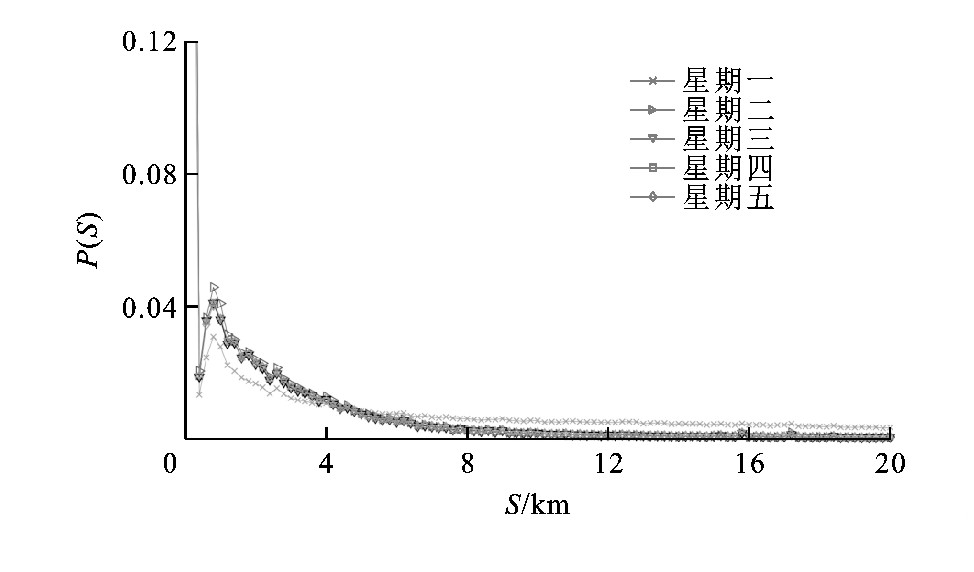
图4、5分别为使用t=1min, s=0.2km作为切片参数, 制作T∈ (0, 1 440]min, S∈[0, 20]km的工作日T序列和S序列, 为突出重点, T∈ (800, 1 440]min的部分未展示。由图4可见:工作日5个T序列间基本重叠, 经计算Hx, y≤0.065, 在[0, 1]区间的左端, 客观反映了T变量的稳定性。由图5可见:S序列也基本重叠, 经计算Kx, y≤0.085, 也在[0, 1]区间的左端, 客观反映了S变量的稳定性。
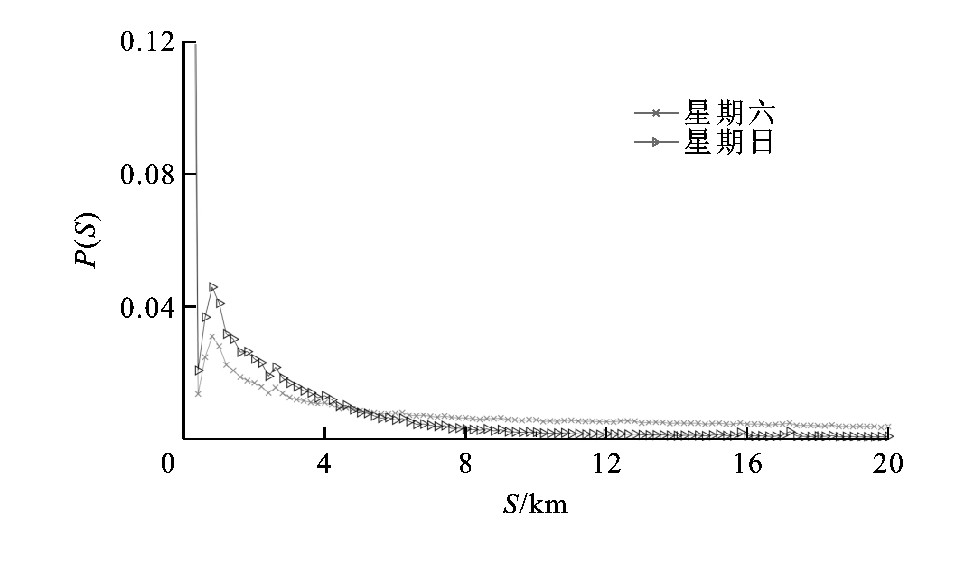
图6、7分别为非工作日的T序列和S序列。由图6可见:星期六和星期日的T序列也基本重叠, 经计算Hx, y=0.130, T序列在工作日和非工作日都稳定。由图7可见:星期日S序列与一周中的其他天有差异, 经计算Kx, y=0.487, 但曲线整体变化趋势也基本一致。
基于序列稳定性, 认为T和S序列是公交系统的一种规律, 可选择某单日序列代表整体情况用于分析。
3.3 换乘行为相关参数确认
3.3.1 转乘时长阈值
图4、6中, T序列在t=21min有一个突变点, 由陡峭变为平缓 (序列拟合函数f (t) 的导函数df (t) /dt<10-4) , 21min处突变只能用转乘来合理解释, 大量乘客因不能一站抵达目的地, 被迫离开公交系统一段时间, 这个时长与有目的滞留在统计中表现出很大差异, 形成一个突变点, 该突变与Bagchi等完成的3个研究中所使用的30min转乘判据非常一致[13,15,16], 因为21~30min之间的积分值非常低, 这个区间的转乘数量几乎可以忽略。
3.3.2 站点间非机动化转移容忍距离
图5、7中, S序列曲线在[0, 0.4]km是迅速衰减的, 代表了公交转乘站台距离的统计特征, 但在S=0.8km出现一个峰, 这个现象的合理解释是, 持卡人选择线路时克服距离, 到邻近站点乘车的行为。假定邻近站点转移行为在S=0.8km两侧是正态分布的, 左侧μ-3σ (μ为期望值, σ为标准差) , 在S=0.8km则右侧μ+3σ界限是T=1.6km。当然, 邻近站点转移距离的概率分布不一定符合这种猜测, 但没有更好的方法推测这个分布。王宁对上海居民步行距离进行研究, 结论是步行出行阈值是1.5km[27]。本文样本数据为2016年8月, 共享单车普及程度不高, 持卡人站点间移动以步行为主, 选择将S=1.6km设定为北京市非机动化转移容忍距离 (直线距离) , 与上海步行出行阈值较一致。实际上曲线[0, 1.6]km区间积分值为0.607, 即60.7%的持卡人会在1.6km内再次进入公交系统, 近40%的持卡人在这个情况下可能使用了公共交通之外的交通工具。
3.3.3 通勤出行与非通勤出行的时长分界
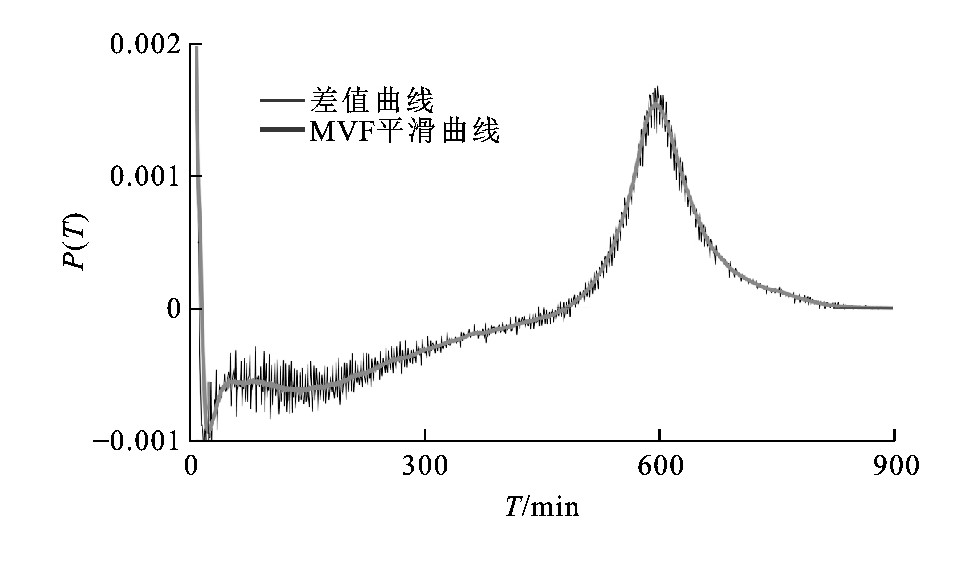
选择一个工作日与非工作日T序列做差值, 在[500, 700]min区间工作日断裂点多于非工作日, 众数出行在T=600min左右, 这个区间的分布符合图2中就业通勤特征。图8为差值序列做移动平均滤波处理结果 (步长为10min) , 在T=478min时P (T) 为0, 为突出特征, T∈[900, 1 440]min区间的差值序列没有展示。由图8可见:T=478min是工作日和非工作日发生不一致的断裂时长点。推定T=478min为非通勤出行和通勤出行时长分界。
差值序列P (T) 和概率拟合分布积累函数CDF (T) 见图9, 可见:差值序列接近μ=601, σ=44的正态分布 (R2=0.93) , 该样本数据中通勤持卡人在就业地滞留时长为 (557, 645) min, 这个区间理论概率为0.997。
3.3.4 转乘时长阈值
差值T序列平滑曲线在T=22min出现1个极小值, 与T序列的突变点21min基本一致, 印证了前文通过突变点对转乘时长阈值21min的推测。本文以22min作为样本数据的转乘时长阈值。
3.3.5 非通勤出行的时长阈值
差值T序列平滑曲线在T为48、140min出现2个拐点。T=48min的合理解释是非通勤出行的左侧边界, T=140min为非通勤出行众数, 即非通勤出行在站点间的最大概率时长是140min, 见图8。T∈[22, 47]min之间的断裂时长是转乘和短时出行目的地的可能性都有, 研究中可以根据实际情况和容差程度处理该范围的断裂点。
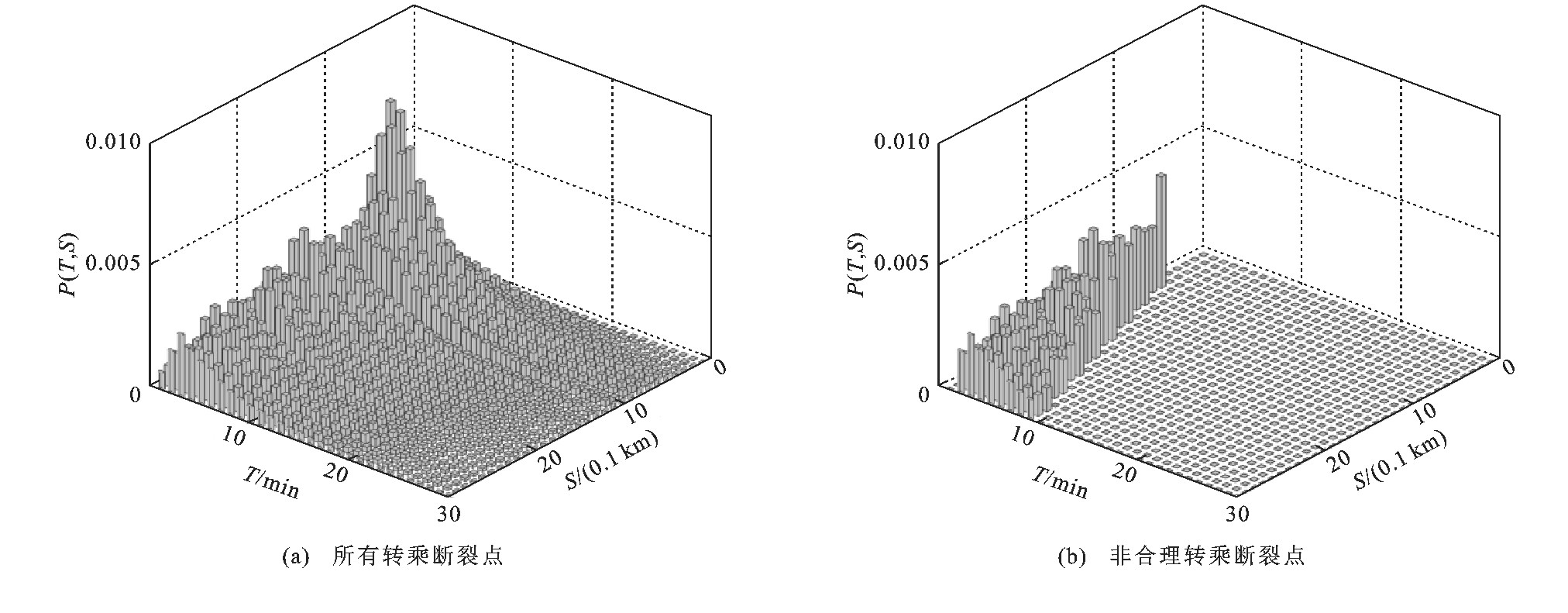
3.4 合理转乘断裂点的校验
使用参数t=1min, s=0.1km, T∈ (0, 30]min, S∈[0, 3]km制作精确T-S矩阵, 见图10 (a) 。若将0.2km·min-1 (高于成年人舒适徒步速度[28], 接近慢速骑行) 作为非机动车转移速度检验标准, 可筛选出不符合非机动化转移校验的断裂点, 见图10 (b) 。这些断裂点可能包含一些错误噪音数据和错漏刷卡情况。持卡人借助公交系统之外机动化交通工具导致校验不符合步行或骑行在站点间转移T和S组合, 在分析转乘行为时需要特别注意。这种现象本身也反映持卡人对公共交通较低依赖的属性。
T-S矩阵可方便地校验站点间合理转乘, 在北京市一天的公交刷卡数据中, 若以S/T>0.2km·min-1为标准, 可识别1 091 858个不符合校验规则的非合理转乘断裂点, 这些断裂点即使在S<1.6km范围, 也不是转乘, 因为T与S两者关系不符合逻辑。这些断裂点在S>1.6km范围则可能借助了其他快速交通工具。
3.5 断裂点分析法的识别及分类效果检验
选择2016年8月17日的刷卡数据进行检验, 检验数据中共6 462 882个断裂点, 若以单一时长法小于22min为条件, 筛选出转乘行为为1 953 336个。若以S>1.6km为传统的单一时长参数筛选, 得出81 011个非合理转乘断裂点。以478min为界限, 采用时长与同站2个判据判断通勤的方法筛选出1 023 849次通勤出行, 若结合本文方法中S<1.6km的参数筛选, 识别出通勤行为增至1 295 164个。识别量的增加主要体现在断裂点分析法对持卡人抵达某地从邻近站点离开行为的有效捕捉, 而传统方法多以同站为主要依据, 未考虑持卡人在站点间的转移。本文方法还可筛选出1 042 255个地面公交和地铁之间的断裂点行为与对公交依赖度低的1 324 242个出行断裂点行为 (以S>1.6km为判据) 。这些检验结果输出对应的识别率见表2, 可见:较现有方法, 断裂点分析法对地面公交与地铁接驳及公交依赖低的情况能够较好识别, 同时对通勤与非通勤换乘分类识别也有所改善。
表 2 识别率Table 2. Recognition rate
4. 结语
(1) 公共交通换乘链断裂点被忽略的断裂时长和断裂位移具有较稳定的统计分布。断裂点特征分类法可基于统计定量地给出转乘行为的时长阈值和位移阈值。断裂点分析法不仅能识别转乘与通勤行为, 还可探讨非通勤出行的时长特征。平行处理地面公交与地铁数据对换乘行为识别分类是有必要的。基于北京市公共交通数据样本发现:北京转乘公交行为过程的时长为0~21min, 60.7%的断裂点中持卡人在1.6km内再次进入公交系统;通勤出行的持卡人滞留在就业地的时长为557~645min, 最大概率出现在601min附近;非通勤出行滞留在目的地时长为48~478min, 最大概率出现在140min附近;20.5%的断裂点持卡人借助了非公共交通方式。
(2) 与现有方法相比, 断裂点分析法考虑了T和S两者关联, 对转乘行为能够更合理更高效地识别。断裂点分析法可根据不同城市公共交通运行实际状况, 计算符合城市实际情况的公交换乘行为分类参数, 例如对共享单车替代步行的情况, 断裂点分析方法可通过调整站点转移容忍速度参数, 应对交通环境的变化。方法不仅可用于交通需求与优化, 对断裂点地理坐标、断裂时长、断裂频次与行为分类的组合, 还可拓展持卡人属性。基于对持卡人属性的聚类, 可更好地解析城市空间功能, 为交通运输规划决策提供支持。
(3) 刷卡数据虽然整体反映了公交系统运行状况, 但非刷卡乘车、刷卡时间与实际下车时间不符、漏刷卡等现象也存在, 数据的质量对识别分类会产生影响;一些城市缺少下车刷卡记录[4], 有的城市发放临时卡或多运营商之间数据的不统一[4,5,29,30]等客观情况干扰了换乘链的制作;2016年年底至2017年共享单车迅速普及, 断裂点分析法参数确认是基于实际统计的结果, 能应对骑行对换乘行为分类参数的干扰, 但骑行通勤的增加会降低公交通勤的识别率。此外, 研究中未开展实地调查, 若用于实际的交通运输规划, 还需补充有效性检验, 以进一步完善研究方法。
-
表 1 换乘链断裂点时空信息分类
Table 1. Classification of TCB spatial and temporal information

表 2 识别率
Table 2. Recognition rate

-
[1] KUSAKABE T, IRYO T, ASAKURA Y. Estimation method for railway passengers'train choice behavior with smart card transaction data[J]. Transportation, 2010, 37 (5): 731-749. doi: 10.1007/s11116-010-9290-0 [2] BAGCHI M, WHITE P R. What role for smart-card data from bus systems?[J]. Municipal Engineer, 2004, 157 (1): 39-46. doi: 10.1680/muen.2004.157.1.39 [3] DEVILLAINE F, MUNIZAGA M, TRÉPANIER M. Detection of activities of public transport users by analyzing smart card data[J]. Transportation Research Record, 2012 (2276): 48-55. [4] 龙瀛, 孙立君, 陶遂. 基于公共交通智能卡数据的城市研究综述[J]. 城市规划学刊, 2015 (3): 70-77. https://www.cnki.com.cn/Article/CJFDTOTAL-CXGH201503010.htmLONG Ying, SUN Li-jun, TAO Sui. A review of urban studies based on transit smart card data[J]. Urban Planning Forum, 2015 (3): 70-77. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CXGH201503010.htm [5] PELLETIER M P, TRÉPANIER M, MORENCY C. Smart card data use in public transit: a literature review[J]. Transportation Research Part C: Emerging Technologies, 2011, 19 (4): 557-568. doi: 10.1016/j.trc.2010.12.003 [6] WANG Wei, ATTANUCCI J P, WILSON N H M. Bus passenger origin-destination estimation and related analyses using automated data collection systems[J]. Journal of Public Transportation, 2011, 14 (4): 131-150. doi: 10.5038/2375-0901.14.4.7 [7] 金凤君. 基础设施与人类生存环境之关系研究[J]. 地理科学进展, 2001, 20 (3): 276-285. doi: 10.3969/j.issn.1007-6301.2001.03.011JIN Feng-jun. Infrastructure and the living environment of human being[J]. Progress in Geography, 2001, 20 (3): 276-285. (in Chinese). doi: 10.3969/j.issn.1007-6301.2001.03.011 [8] MA Xiao-lei, WU Yao-jan, WANG Yin-hai, et al. Mining smart card data for transit riders'travel patterns[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 1-12. doi: 10.1016/j.trc.2013.07.010 [9] TRÉPANIER M, TRANCHANT N, CHAPLEAU R. Individual trip destination estimation in a transit smart card automated fare collection system[J]. Journal of Intelligent Transportation Systems, 2007, 11 (1): 1-14. doi: 10.1080/15472450601122256 [10] BESSER L M, DANNENBERG A L. Walking to public transit: steps to help meet physical activity recommendations[J]. American Journal of Preventive Medicine, 2005, 29 (4): 273-280. doi: 10.1016/j.amepre.2005.06.010 [11] FU Xue-mei, JUAN Zhi-cai. Understanding public transit use behavior: integration of the theory of planned behavior and the customer satisfaction theory[J]. Transportation, 2017, 44 (5): 1021-1042. doi: 10.1007/s11116-016-9692-8 [12] NASSIR N, HICKMAN M, MA Zhen-liang. Activity detection and transfer identification for public transit fare card data[J]. Transportation, 2015, 42 (4): 683-705. doi: 10.1007/s11116-015-9601-6 [13] BAGCHI M, WHITE P R. The potential of public transport smart card data[J]. Transport Policy, 2005, 12 (5): 464-474. doi: 10.1016/j.tranpol.2005.06.008 [14] 吴祥国. 基于公交IC卡和GPS数据的居民公交出行OD矩阵推导与应用[D]. 济南: 山东大学, 2011.WU Xiang-guo. Urban public transportation trip OD matrix inference and application based on bus IC card data and GPS data[D]. Jinan: Shandong University, 2011. (in Chinese). [15] ALSGER A A, MESBAH M, FERREIRA L, et al. Use of smart card fare data to estimate public transport origindestination matrix[J]. Transportation Research Record, 2015 (2535): 88-96. [16] ALI A, KIM J, LEE S, Travel behavior analysis using smart card data[J]. KSCE Journal of Civil Engineering, 2016, 20 (4): 1532-1539. [17] FARBER S, FU Li-wei. Dynamic public transit accessibility using travel time cubes: comparing the effectsof infrastructure (dis) investments over time[J]. Computers, Environment and Urban Systems, 2017, 62: 30-40. doi: 10.1016/j.compenvurbsys.2016.10.005 [18] BACHAND-MARLEAU J, LEE B H Y, EL-GENEIDY A M. Better understanding of factors influencing likelihood of using shared bicycle systems and frequency of use[J]. Transportation Research Record, 2012 (2314): 66-71. [19] MOHANTY S, BANSAL S, BAIRWA K. Effect of integration of bicyclists and pedestrians with transit in New Delhi[J]. Transport Policy, 2017, 57: 31-40. doi: 10.1016/j.tranpol.2017.03.019 [20] AGARD B, MORENCY C, TRÉPANIER M. Mining public transport user behaviour from smart card data[J]. IFAC Proceedings Volumes, 2006, 39 (3): 399-404. [21] 龙瀛, 张宇, 崔承印. 利用公交刷卡数据分析北京职住关系和通勤出行[J]. 地理学报, 2012, 67 (10): 1339-1352. doi: 10.11821/xb201210005LONG Ying, ZHANG Yu, CUI Cheng-yin. Identifying commuting pattern of beijing using bus smart card data[J]. Acta Geographica Sinica, 2012, 67 (10): 1339-1352. (in Chinese). doi: 10.11821/xb201210005 [22] TAO Sui, ROHDE D, CORCORAN J. Examining the spatialtemporal dynamics of bus passenger travel behavior using smart card data and the flow-comap[J]. Journal of Transport Geography, 2014, 41: 21-36. doi: 10.1016/j.jtrangeo.2014.08.006 [23] CHO S, LEE W D, HWANG J H, et al. Validation of activity-based travel demand model using smart-card data in Seoul, South Korea[J]. Procedia Computer Science, 2015, 52: 707-712. doi: 10.1016/j.procs.2015.05.080 [24] GUERRA E. Mexico City's suburban land use and transit connection: the effects of the Line B Metro expansion[J]. Transport Policy, 2014, 32: 105-114. doi: 10.1016/j.tranpol.2013.12.011 [25] WANG Zi-jia, LIU Yan, CHEN Feng. Evaluation and improvement of the interchange from bus to metro using smart card data and GIS[J]. Journal of Urban Planning and Development, 2018, 144 (2): 1-8. [26] MISHRA S, WELCH T F, TORRENS P M, et al. A tool for measuring and visualizing connectivity of transit stop, route and transfer center in a multimodal transportation network[J]. Public Transport, 2015, 7 (1): 77-99. doi: 10.1007/s12469-014-0091-2 [27] 王宁, 杜豫川. 社区居民适宜步行距离阈值研究[J]. 交通运输研究, 2015, 1 (2): 20-24, 30. https://www.cnki.com.cn/Article/CJFDTOTAL-JTBH201502004.htmWANG Ning, DU Yu-chuan. Resident walking distance threshold of community[J]. Transport Research, 2015, 1 (2): 20-24, 30. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JTBH201502004.htm [28] BOHANNON R W. Comfortable and maximum walking speed of adults aged 20-79 years: reference values and determinants[J]. Age and Ageing, 1997, 26 (1): 15-19. doi: 10.1093/ageing/26.1.15 [29] ASAKURA Y, IRYO T, NAKAJIMA Y, et al. Estimation of behavioural change of railway passengers using smart card data[J]. Public Transport, 2012, 4 (1): 1-16. doi: 10.1007/s12469-011-0050-0 [30] ALSGER A, ASSEMI B, MESBAH M, et al. Validating and improving public transport origin-destination estimation algorithm using smart card fare data[J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 490-506. doi: 10.1016/j.trc.2016.05.004 -





 下载:
下载:










 下载:
下载: