0.   引言

地铁具有运量大、速度快、准点、环保、节能等优点, 世界许多大城市建设了地铁。然而地铁客流巨大, 其一旦发生恐怖袭击、火灾等事故将造成重大的生命和财产损失。1995年7月25日, 法国巴黎地铁列车发生爆炸事件, 8人死亡, 117人受伤; 2011年9月27日, 上海10号线发生列车追尾, 造成284人受伤。地铁一旦发生重大事故, 如何在最短时间内开展紧急救援, 减少生命财产损失, 是各级政府和部门关心的首要问题。

对地铁应急救援的研究源自于现实需求, 最早的研究始于1998年东京地铁沙林毒气案, Okumura等从应急管理、医疗机构响应角度总结了地铁救援的教训与经验^{[1, 2]}。此后, 针对2003年韩国大邱地铁纵火案为背景的地铁救援医疗^[3]、疏散仿真也应运而生^[4], 后续的研究更多地集中在地铁隧道火灾烟气控制^{[5, 6, 7, 8]}、地铁乘客疏散时间^{[9, 10, 11, 12, 13]}, 未涉及如何利用专业设备开展地铁减灾救援问题。实际上, “赤手空拳”地开展地铁减灾救援几乎是不可能的, 只能利用现代化的专用救援设备开展此类救援。然而, 地铁隧道空间狭窄, 医疗、消防等设备体积与质量较大, 难以甚至无法依靠人力背负进入隧道施救, 这导致地铁救援困难重重, 救援成功率往往较低^{[14, 15]}。

对此, 适宜地铁隧道开展救援的专用车辆应运而生。地铁专用救援车目前有3类: 第1类是路轨两用救援车, 该类车同时安装了适宜路面和轨道行驶的橡胶轮和轨道轮, 可在道路快速行驶, 也可以由地面驶上轨道, 并以轨道轮驶入地铁隧道开展救援, 这类车辆载重能力强、行驶速度快, 但价格相当昂贵(每辆约750万元), 目前仅北京、上海、南京、武汉等极少数城市购置; 第2类是地铁专用救援车, 本质上是由电池驱动的轨道便捷式平板车, 仅能沿轨道移动到事故现场, 该类车辆移动速度慢, 装载空间及载重量均较小, 但是可以由邻近地铁站置放于轨道上, 再驶向灾害事故地点, 布置较为灵活, 2005年伦敦地铁爆炸案便使用了该类救援车抢救了伤员; 第3类为履带式轨道专用消防车, 该车目前仅有陆虎公司生产, 其一般停放于地铁消防局或车辆段, 事故发生时由消防员遥控驾驶到事故区段, 消防员可在数百米外遥控其灭火, 灭火性能强, 售价亦很昂贵(每辆180万元), 目前北京、上海等城市购置了履带式救援车。可以预期, 随着中国地铁通车总里程快速增加, 地铁救援的重要性日益凸显, 针对地铁专用救援车辆的选购、配置及调度将成为地铁减灾的重要议题。然而, 通过查阅各类文献发现相关研究极为匮乏, 地铁救援车辆的规划与调度缺乏必要的决策依据与方法。

尽管缺乏地铁救援车辆规划与调度研究, 但是有关医疗急救、消防救援车辆规划的研究却较为丰富。早期的研究主要包括救援车辆的覆盖度问题和中值问题, 前者试图优化救援车布设位置, 确保每个呼叫救援点至少有1辆救援车能提供救援; 后者主要试图将救援车到达事故发生地之间的平均行程时间最小化。救援系统的关键指标是响应时间, 即接到救援电话后救援车到达事故现场的时间, 因此, 更多的研究也就集中在减少响应时间的中值模型上。Hakimi最早提出了多设施中值选址问题, 即选定一个或多个设施的位置使得设施点与事发地点间的最大距离最小化^[16]; Calvo等在此基础上研究了救援车选址优化^{[17, 18, 19]}。由于早期的选址模型都是确定性的, 而事故的发生总是呈现相当的随机性, 此时即使在平均意义上救援车辆能满足救援需求, 在实际中仍然会出现救援车辆短期供给不足的情形^[20], 因此, 通过在救援需求、行程时间等方面考虑拥挤(即辖区内的救援车辆繁忙而暂时无法响应救援需求的情形) 概率的随机性模型应运而生。由于拥挤会显著影响救援绩效, 在规划救援车辆时应重点加以考虑^[21]。救援车辆堵塞的规划模型包括平均覆盖度最大化问题^[21]与备用车辆覆盖度最大问题^[22]两大类, 其中前者包括救援车辆的行程速度变化^[23]、行程时间变化^[24], 后者包括以排队论估计救援车辆繁忙比例、考虑救援需求的排队个数限制等。基于中国铁路组织机构的特点和应急救援现状, 吴艳华等以最小救援基地总成本和最短救援响应时间为双目标函数, 以最大服务距离为约束条件, 建立了铁路救援基地多目标层级规划选址模型^[25]。值得注意的是, 上述研究均假定各小区的救援车辆仅负责本区域的救援, 而不能处理跨小区的救援情形^[26]。实际中, 由于负责某些小区的车辆处于繁忙状态, 小区内如果发生救援请求, 只能指派最近的其他小区的空闲车辆出警, 此类情形在消防、治安、医疗救护等方面普遍出现, 因此, 紧急救援系统必须能考虑救援车辆跨区域救援的情形^[27]。

如果地铁网络配置专用救援车辆, 一方面受制于高昂的售价而难以大量采购; 另一方面, 地铁灾害属小概率事件, 没有必要大量采购此类消防车, 因此, 地铁网络只能少量配置专用救援车, 此时跨区域救援几乎成为必然。如何根据地铁事故频率, 合理配置地铁专用救援车辆需要科学的决策依据与方法。而地铁事故的救援涉及到救援车辆规划和调度两方面, 为了能明晰地建立地铁救援车辆运作过程的模型, 本文开展如下研究: 分析地铁事故救援车辆的配置问题与调度过程, 从而将地铁救援过程转化为生灭过程; 根据随机过程理论, 建立应急救援车辆联合排队模型, 设计算法求解救援车辆工作状态概率; 将所建模型作为分析工具, 计算地铁救援系统的各类绩效指标, 展现其在地铁救援车辆规划中的应用。

1.   地铁救援车辆联合排队模型

1.1   地铁救援车辆运作过程分析

为了不失一般性, 本文以路轨两用救援车为例, 说明地铁救援车辆的运作过程。为了提高救援效率, 一般将地铁线网划分为J个救援小区, 每个小区配若干辆救援车辆, 共有N辆救援车辆。假设地铁线网第i个小区的事故发生速率为λ_i; 小区i到小区j的平均行程时间为t_ij, 其中i, j=1, 2, …, J。当小区地铁发生事故, 系统将指派最近的救援车辆, 一般为部署在该小区的救援车辆进行救援, 如果该小区的救援车辆都处于忙碌状态, 将从离事发地点最近的其他小区指派空闲的救援车辆进行救援。当救援车辆处理完该事故时, 救援车辆的状态又变为空闲, 本质上, 地铁救援系统的运行过程属于复杂的地铁救援车辆联合排队问题。

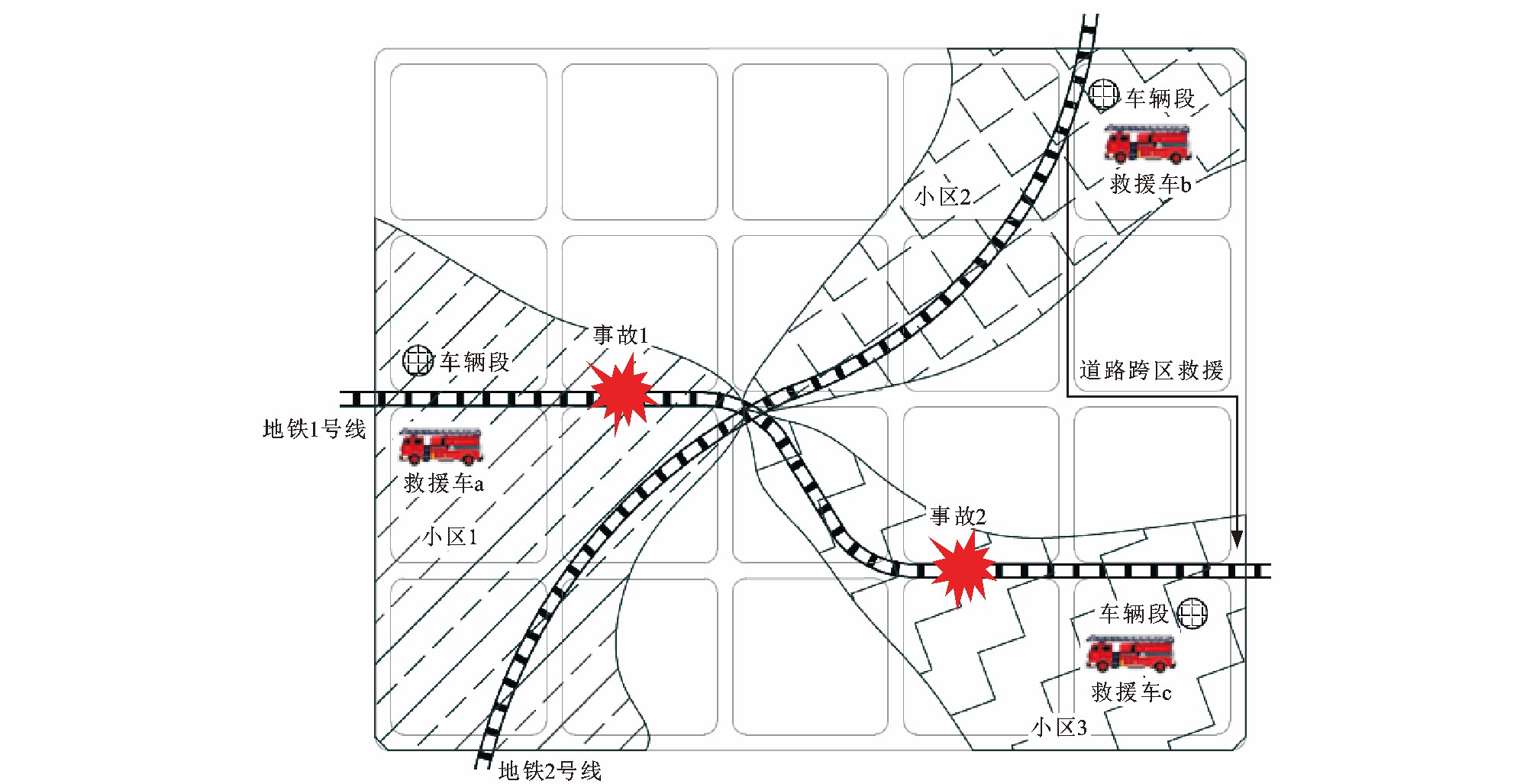
为了更清晰地说明地铁救援的运作过程, 以图 1举例说明: 将地铁1号线和2号线划分成3个小区, 对应小区1、2和3的图案阴影, 3辆路轨两用救援车a~c分别布置在3处地铁车辆段位置; 根据上述救援车辆指派原则, 当事故1发生时, 路轨两用救援车a可以从车辆段直接进入地铁到达事故现场进行救援; 当发生事故2时, 应由路轨两用救援车c前往救援, 但如果此时路轨两用救援车c正处于救援前一事故的繁忙状态(即车辆正在施救或正在前往事故地点途中), 该车辆段无车可派时, 则可以指派路轨两用救援车b从道路行驶, 跨区到事故2的地点进行救援。当地铁在不同的小区短时内发生多起事故时, 负责本区段的车辆有可能出现无车可派的情形, 此时, 只能派遣其他小区且空闲的车辆跨区救援。由上述的救援车辆运作过程可知: 救援车辆布设位置、配车数量与地铁救援区段划分将会影响到各救援车辆的工作强度和救援系统平均响应时间, 决定着地铁救援的效果。

1.2   应急救援排队过程的定义

根据1.1节的分析可知, 救援车辆有2种状态: 繁忙或空闲。为此, 定义b_n为第n辆救援车的状态, 用b_n=0表示该救援车辆为空闲状态, 用b_n=1表示该救援车辆为忙碌状态。对于系统中所有N辆救援车, 可以用N位二进制数来表示这N辆救援车的救援状态, 即B={b_N, b_N-1, …, b₁}, 故共有2^N个状态, 而每个B_υ状态对应着唯一的十进制值υ, 即υ=2^N-1b_N+2^N-2b_N-1+…+b₁。

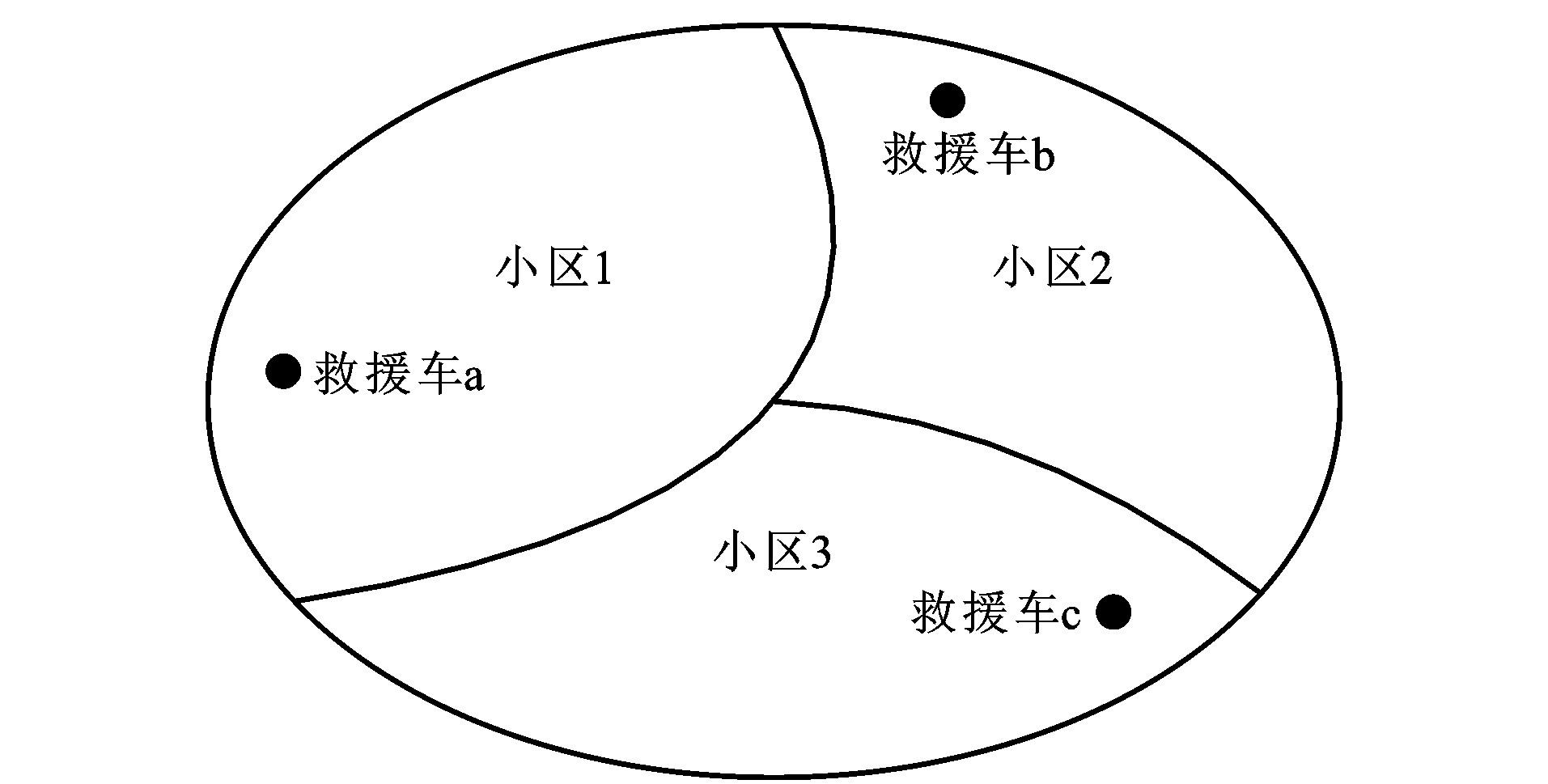
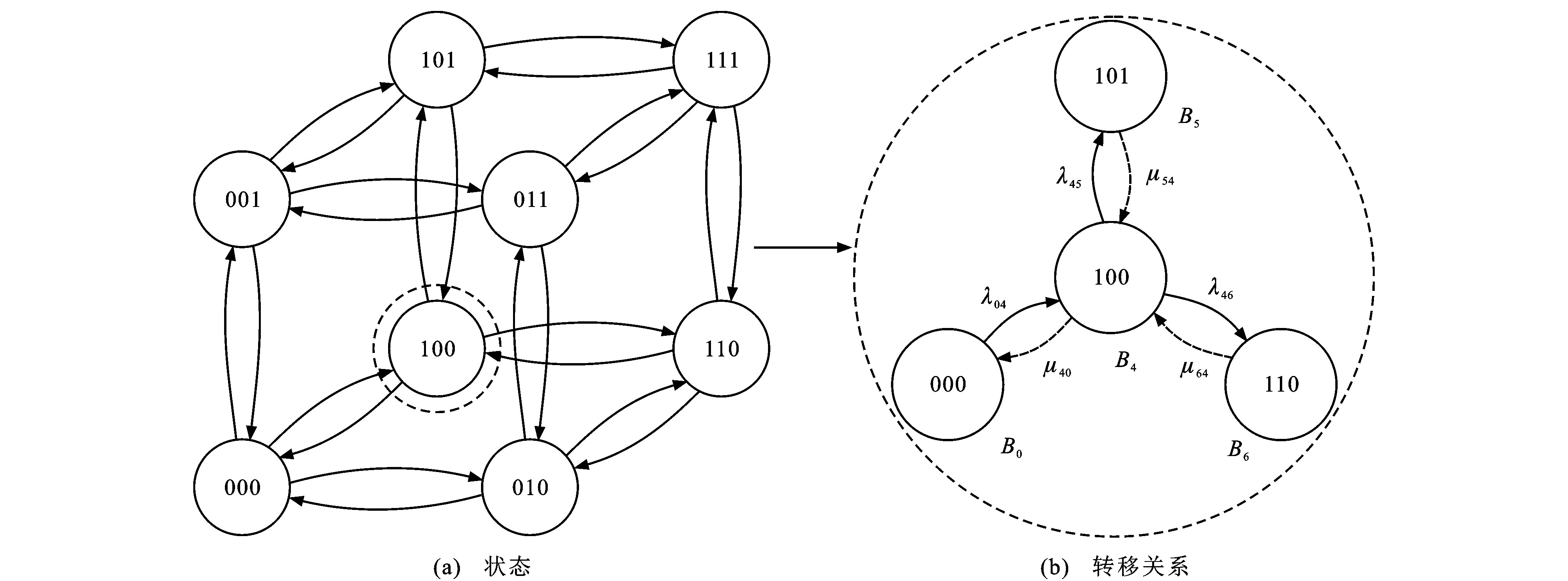
为了遍历救援车辆所有可能出现的状态空间, 时间间隔足够小, 确保1个时间间隔内仅能有1辆救援车响应1次紧急呼叫, 或者结束1次救援, 那么救援车辆的状态便从1变为0, 或者从0变为1。对于有N辆救援车辆的系统而言, 每个状态就可以向固有的N个状态发生变化。以图 2所示的由3辆救援车辆构成的救援系统为例, 将区域分成3个小区, 每个小区由1辆救援车辆负责救援, 则所有救援车辆的状态数一共有2³=8个。图 3(a)给出了救援车状态空间及其转移关系, 而图 3(b)为状态B₄与其他3个状态之间的状态转移关系, 其中μ₅₄为状态B₅到状态B₄的转移速率; λ₄₅为状态B₄到状态B₅的转移速率; μ₄₀为状态B₄到状态B₀的转移速率; λ₀₄为状态B₀到状态B₄的转移速率; μ₆₄为状态B₆到状态B₄的转移速率; λ₄₆为状态B₄到状态B₆的转移速率。根据图 3, 每个状态可以向相邻的3个状态转换。如果2辆救援车辆状态发生改变, 则必须依次进行两步转换。从数学角度来看, 应急救援车辆的运作过程本质上从1个状态转变为另1个状态。

图  1  路轨两用救援车分布

Figure  1.  Deployment of road-rail rescue vehicles

下载: 全尺寸图片 幻灯片

图  2  应急救援车辆空间分布

Figure  2.  Deployment of emergency rescue vehicles

下载: 全尺寸图片 幻灯片

图  3  三辆救援车辆的救援状态转移

Figure  3.  Transitions between rescue states of 3 rescue vehicles

下载: 全尺寸图片 幻灯片

1.3   随机过程的状态分析

为了更好地描述模型中的两类状态转换, 令B_r和B_s分别为十进制状态r、s (r≠s) 所对应的二进制状态。令w (B_r) =∑b_n表示状态B_r中处于繁忙状态的救援车数量, d_rs为状态B_r和状态B_s之间的海明距离, 且d_rs=d_rs⁺+d_rs^-, 其中, d_rs⁺=w (B_r^′∩B_s) 为向上的海明距离, d_rs^-=w (B_r∩B′_s) 为向下的海明距离。对于状态B_r, 只要d_rs⁺=1, 则向上的转移可以发生在所有相邻的B_r上, 向下转移亦同理。令λ_rs为状态B_r向上转移到状态B_s的平均速率, μ_rs为状态B_r向下转移到状态B_s的平均速率, 假设救援车辆的救援速率相等且均为μ, 系统的状态完全由B_r指定, 该模型是一个有限状态连续时间的马尔科夫过程, 那么系统状态的流入速率(该系统由其他状态变化到当前状态的转移速率之和) 应等于流出速率(当前状态转移到其他状态的速率之和), 救援系统状态方程为

$\begin{array}{l}{\rm P}(B{}_r)\left[{\displaystyle \sum _{B{}_s\in \{C{}_{{\rm N}}d{}_{rs}^{+}=1\}}\lambda }{}_{rs}+\mu w(B{}_r)\right]={\displaystyle \sum _{B{}_r\in \{C{}_{{\rm N}}d{}_{rs}^{-}=1\}}\mu }{\rm P}(B{}_s)+\\ {\displaystyle \sum _{B{}_t\in \{C{}_{{\rm N}}d{}_{tr}^{+}=1\}}\lambda }{}_{tr}{\rm P}(B{}_t)(1)\end{array}$

式中: P (B_r)、P (B_s)、P (B_t) 分别为系统处于状态B_r、B_s、B_t时的概率; $B_{r} \in\left\{C_{N} \mid d_{r s}^{-}=1\right\}$为满足与状态B_s之间存在向下海明距离为1的所有状态B_r; $B_{t} \in\left\{C_{N} \mid d_{s}^{+}=1\right\}$为满足与状态B_s之间存在向上海明距离为1的所有状态B_t; $B_{t} ; B_{s} \in\left\{C_{N} \mid d_{n}^{+}=1\right\}$为满足与状态r之间存在向上海明距离为1的所有状态s。

假定κ_rj是在状态B_r和小区j下最优响应车辆的数量。那么对于与状态B_r和小区j相关的d_rs⁺=1的状态, 转移速率会增加λ_j/κ_rj, 即

$\lambda {}_{rs}=\lambda {}_{rs}+\lambda {}_j/\kappa {}_{rj}(2)$

另外, 所有状态的概率和必须为1, 即

${\displaystyle \sum _{r=0}^{2{}^{{\rm N}}-1}{\rm P}}(B{}_r)=1(3)$

为更好地理解上述方程, 根据图 3中的放大部分可知, 与状态B₄可以直接发生转换的状态包括B₅、B₆和B₀。而状态B₄的进出速率应保持平衡, 即状态B₄的流出速率与流入速率应相等, 则状态B₄的救援系统状态平衡方程为

$\begin{array}{l}{\rm P}(B{}_4)(\lambda {}_{45}+\lambda {}_{46}+\mu {}_{40})=\lambda {}_{04}{\rm P}(B{}_0)+\\ \mu {}_{54}{\rm P}(B{}_5)+\mu {}_{64}{\rm P}(B{}_6)\end{array}$

式中: B₄为100;B₅为101;B₆为110;B₀为000。

类似地, 对8个状态均可列出状态平衡方程。

2.   模型求解算法

2.1   基于矩阵压缩的状态概率求解算法

状态平衡式(1) 构成了方程个数及未知数均为2^N的线性方程组。鉴于救援车辆状态空间转换具有特殊的结构, 本文给出救援车辆状态概率值初始解计算方法, 根据状态平衡线性方程组的特征, 提出一种迭代矩阵压缩的迭代求解算法。

对式(1) 构造关于P (B_s) 的迭代。假设P_η (B_r) 为P (B_r) 第η次迭代的估计值(η=0, 1, 2, …), 则式(1) 的Jacobi迭代可表示为

$\begin{array}{l}{\rm P}{}_{\eta }(B{}_r)=[{\displaystyle \sum _{B{}_r\in \{C{}_{{\rm N}}d{}_{rs}^{-}=1\}}\mu }{\rm P}{}_{\eta -1}(B{}_s)+{\displaystyle \sum _{B{}_t\in \{C{}_{{\rm N}}d{}_{tr}^{+}=1\}}\lambda }{}_{tr}{\rm P}{}_{\eta -1}(B{}_t)]\cdot \\ \left[{\displaystyle \sum _{B{}_s\in \{C{}_{{\rm N}}d{}_{rs}^{+}=1\}}\lambda }{}_{rs}+\mu w(B{}_r)\right]{}^{-1}(4)\end{array}$

根据图 3和式(4) 可知: P (B_r) 是由其相邻的(繁忙车辆数相差1) 状态P (B_s) 与P (B_t) 计算得到的, 故式(4) 的迭代求解实际上是通过震荡的方式进行的, 即: 根据前一次迭代的奇/偶数辆繁忙救援车辆状态概率值, 依据式(4) 得到当前偶/奇数辆繁忙救援车辆状态概率值, 这样不断反复迭代, 当满足收敛准则时迭代终止。

对式(4) 进行奇偶交替迭代必须给出救援车辆状态概率初始解P₀ (B_r)。鉴于地铁救援车辆系统本质上为先到先服务的M/M/N排队系统, 则救援系统中k辆救援车同时处于繁忙的概率为

${\rm P}(k)=\frac{(\lambda /\mu ){}^k/k!}{{\displaystyle \sum _{m=0}^{{\rm N}}(\lambda /\mu )}{}^m/m!}k=0,1,\cdots ,{\rm N}(5)$

式中: m为处于繁忙状态的车辆数。

由于P (B₀) 和P (B_2^N-1) 分别等于P (0) 和P (N), 通过归纳法可以证明对于第η次迭代

${\displaystyle \sum _{B{}_n\in {\rm H}{}_k}{\rm P}}{}_{\eta }(B{}_s)={\rm P}(k)k=0,1,\cdots ,{\rm N}(6)$

式中: H_k为有k辆车处于繁忙的车辆状态集合, 即满足∑b_n=k的车辆状态空间集合。

假设对于给定的超平面的所有状态概率是相等的。在总数N辆车中, 由式(6) 可得救援车辆状态概率值初始解为

$\begin{array}{l}{\rm P}{}_0(B{}_n)=\{(\lambda /\mu ){}^{w(n)}/[(w(B{}_n)!)\cdot \\ {\displaystyle \sum _{i=0}^{{\rm N}}\frac{(\lambda /\mu ){}^m}{m!}}]\}[C{}_{{\rm N}}^{w(B{}_n)}]{}^{-1}(7)\end{array}$

式中: w (B_n) 为状态为B_n时繁忙的救援车辆数; C ${}_{{\rm N}}^{w(B{}_n)}$为总数N辆车中有w (B_n) 辆车处于繁忙的所有的组合数, 为

$C{}_{{\rm N}}^{w(B{}_n)}={\rm N}!/\{w(B{}_n)![{\rm N}-w(B{}_n)]!\}(8)$

由于迭代过程中状态转移速率λ_rs所构成的矩阵A的元素数量规模达到2^2N, 所以即使是救援车辆数很小的N也会产生很大的运算量和存储空间, 故本文对矩阵A进行改良。通过观察发现, 由于每次状态转移只改变1辆救援车辆的状态, 所以每个状态只能向固定的N个状态发生转移, 即矩阵每一行有N个元素不为0, 其他元素为0, 当N很大时, 矩阵绝大部分元素为0, 故矩阵A是一个典型的稀疏矩阵, 其有效的数据量为N×2^N。所以设置一个N×2^N的矩阵存储状态转移速率, 来表示相邻的N个顶点之间的有效转换。数值为正表示向上转移, 为负表示向下转移。这样就将矩阵A压缩成N×2^N的矩阵V, 极大地减少了循环遍历的时间。

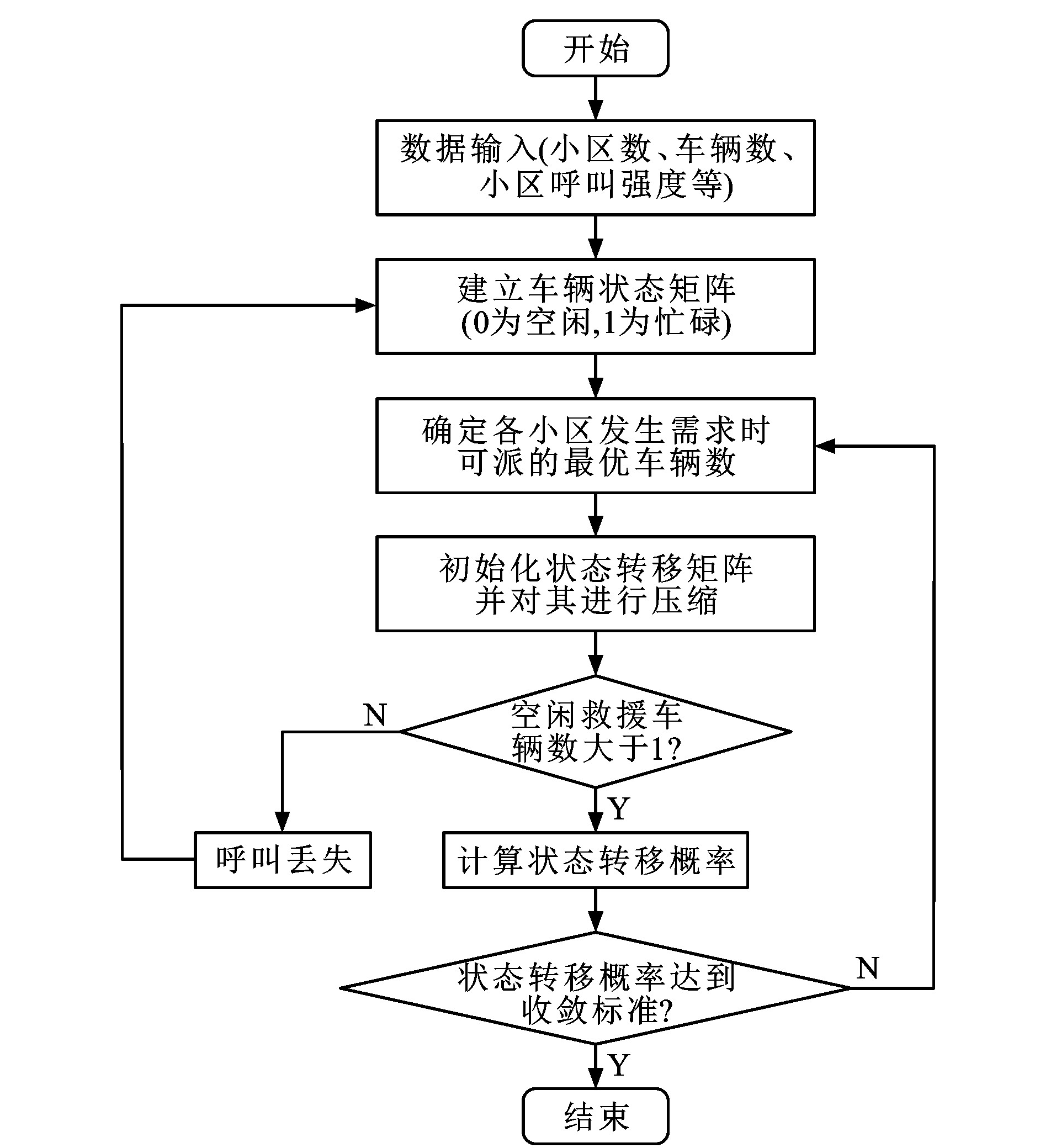
把联合排队模型的数学模型转换成计算机语言的关键在于生成全部救援车辆的状态空间、计算状态间的转移速率及概率。下面是该模型简略的算法步骤和对应的算法流程见图 4。

图  4  算法流程

Figure  4.  Algorithm flow

下载: 全尺寸图片 幻灯片

Step 1: 输入基础数据: 地铁区段的数量及配置救援车辆数量、区段间距离、灾害发生频率。

Step 2: 用二进制数表示车辆的所有状态组合, 遍历所有的车辆状态B={b_N, b_N-1, …, b₁}。

Step 3: 根据小区间的距离t_ij和车辆到各小区的概率, 对车辆到各小区的距离进行排序。

Step 4: 确定状态B_r下小区j产生服务需求时可派去的最优(最快) 救援车的数量κ_rj。

Step 5: 根据车辆状态矩阵初始化状态转移矩阵A, 将其转换成N×2^N的矩阵V。

Step 6: 根据式(2), 对状态转移速率λ_rs赋值。

Step 7: 构造状态概率矩阵P并根据式(6) 对矩阵赋初始值P₀ (B_n)。

Step 8: 根据迭代式(4) 对P_η (B_s) 进行迭代。

Step 9: 计算收敛精度$\epsilon ={\displaystyle \sum _{m=0}^{2{}^{{\rm N}}-1}\parallel }{\rm P}{}_{\eta }(B{}_m)-{\rm P}{}_{\eta -1}(B{}_m)\parallel$ ‖P_η-1 (B_m) ‖, 若ε < 10^-6, 算法结束; 否则返回Step 4。

2.2   地铁救援系统性能指标计算方法

现实中, 地铁救援系统应确保救援车辆到达事发地点时间小于规定阈值, 此外还要求各救援车辆工作强度和区段地铁获得救援的时间均应尽量相当。如果救援车辆工作强度差异较大, 或各分区地铁事故获得救援的时间差异较大, 说明各小区车辆配置不科学, 需要调整地铁救援系统的规划方案。为此本文给出了部分地铁救援性能指标的计算方法。

系统的平均救援响应时间为各救援车辆到达各事发地点的平均行程时间与对应的概率乘积之和, 即

${\rm T}={\displaystyle \sum _{n=1}^{{\rm N}}{\displaystyle \sum _{j=1}^J\rho }}{}_{nj}t{}_{nj}(9)$

式中: t_nj为地铁救援车辆n到达事发小区j的平均行程时间; ρ_nj为派遣车辆n到小区j的概率; T为系统的平均救援响应时间。

救援车辆n的工作强度可衡量分配到各个救援车辆的工作量是否均衡, 即救援车辆n处于救援状态的时间比例。如果出现工作强度特别大的车辆, 则可以考虑在该小区增配车辆。令{n: b_r=1}为所有第n辆车为繁忙的状态集合, 则救援车辆n的工作强度ρ_n可以表示为

$\rho {}_n={\displaystyle \sum _{\{n:b{}_r=1\}}{\rm P}}(B{}_r)(10)$

救援车辆n跨小区调度的概率E_n为

$E{}_n={\displaystyle \sum _{j\ne n}\rho }{}_{nj}/{\displaystyle \sum _{j=1}^J\rho }{}_{nj}(11)$

当一个小区无车可派时, 必须要从别的小区调度车辆, 救援时间大大增加。地区总的跨区比例F表示小区i的救援车辆n响应小区j的概率和, 其数值越大, 表示地区车辆配置越不均衡。地区总的跨区比例F则可以表示为

$F={\displaystyle \sum _{n=1}^{{\rm N}}{\displaystyle \sum _{j\ne n}\rho }}{}_{nj}(12)$

基于地铁救援系统的状态概率计算结果, 还能获得每辆救援车辆的工作量及平均响应时间、每个区的平均出行时间、每个救援小区获得救援的跨区比例等多个救援系统指标。

3.   实例分析

为了体现本文模型的有效性, 以北京地铁1、5号线构成的地铁线网为例, 评价上述3种地铁救援车辆在该线网上的紧急救援绩效指标, 并对具体的救援车辆配置做出评价与分析。

3.1   地铁线网结构

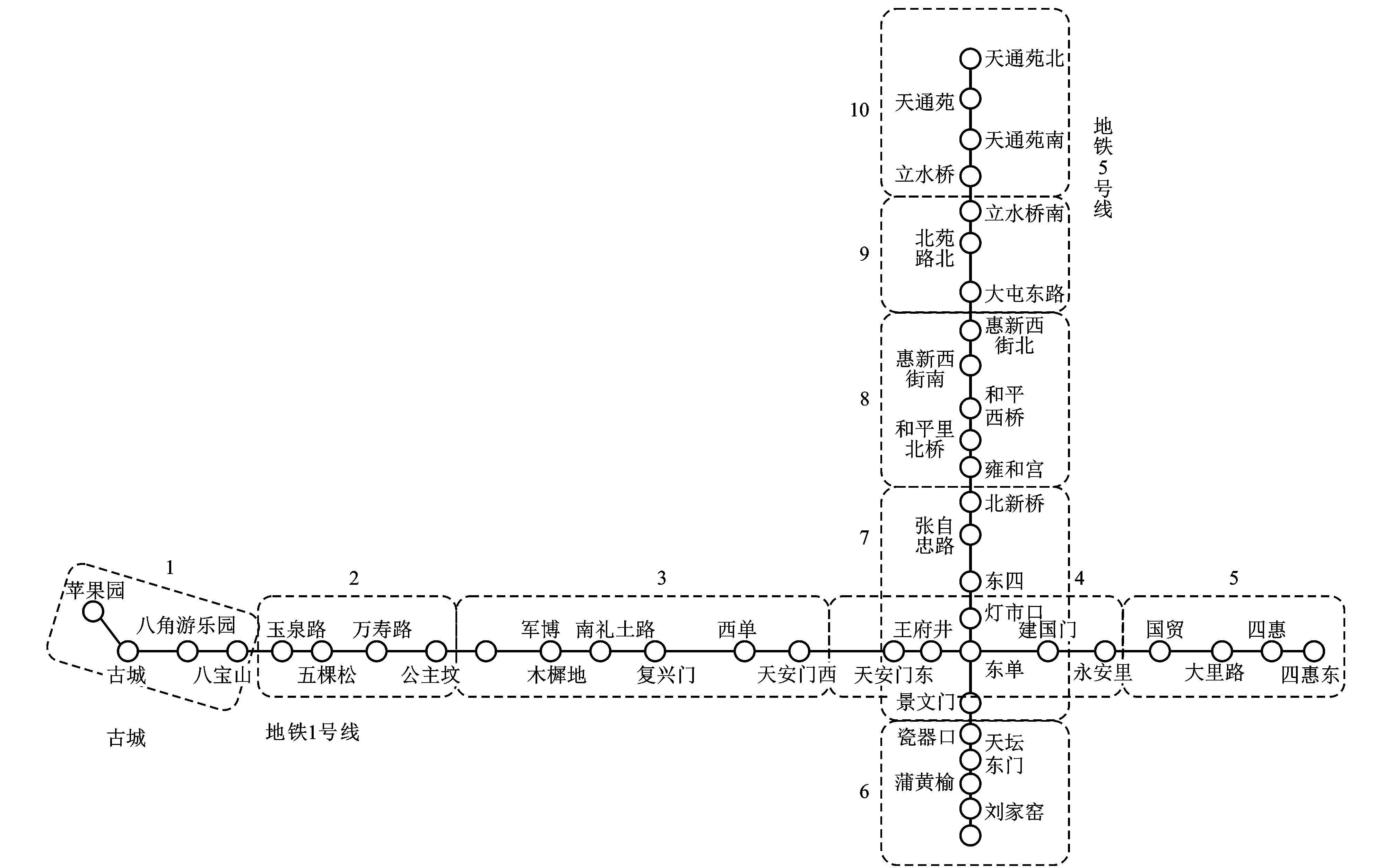
本文以图 5所示的北京地铁1、5号线构成的网络为研究对象, 其中1号线全长31.04 km, 设23个车站和2个车辆段; 5号线全长27.60 km, 设23个车站、1个车辆段和1个停车场。为了应用本文建立的模型, 需要明确地铁线网分区及车辆配置、地铁事故发生频率与各救援小区间行程时间等参数。

采购预算与地铁线网区段划分决定着地铁救援车配置数量与分布。3种地铁救援车型价格、行驶速度相差较大, 其中路轨两用救援车在路面行驶速度最大可达90 km·h^-1, 在轨道行驶速度为40 km·h^-1; 履带式救援车在轨道行驶速度为40 km·h^-1; 便携式轨道救援车在轨道行驶速度为16 km·h^-1。鉴于路轨两用和履带式救援车价格远超便携式地铁救援车, 本文假定路轨两用救援车配置2辆, 履带式救援车配置8辆, 便携式救援车配置20辆, 另外将1号线与5号线各分为图 5的5个的救援区段, 各区段的救援车配置见表 1。

图  5  地铁线网与救援小区

Figure  5.  Railway network and rescue zones

下载: 全尺寸图片 幻灯片

地铁事故发生频率参考表 2所示的2007~2014年北京地铁救援派车与平均现场处理救援的时间。根据表 2的统计, 地铁事故发生频率为6.3×10^-4次·h^-1, 平均救援时间(即在现场处置救援时间) 为24.3 min。

救援车辆可能存在跨小区的调度救援, 因此, 有必要给出各地铁区段间的救援车行程时间。路轨两用救援车和履带式救援车仅能从地铁车辆段进入事发地点, 而便携式救援车可直接在地铁站点施放于轨道上, 因此, 这3类车辆到达事故发生点的路径是不同的。表 3中给出了小区间路轨两用救援车和履带式救援车的行程时间, 表 4中给出了小区间便携式救援车的行程时间, 其余均为路轨两用救援车和履带式救援车的行程时间。

3.2   运行结果分析

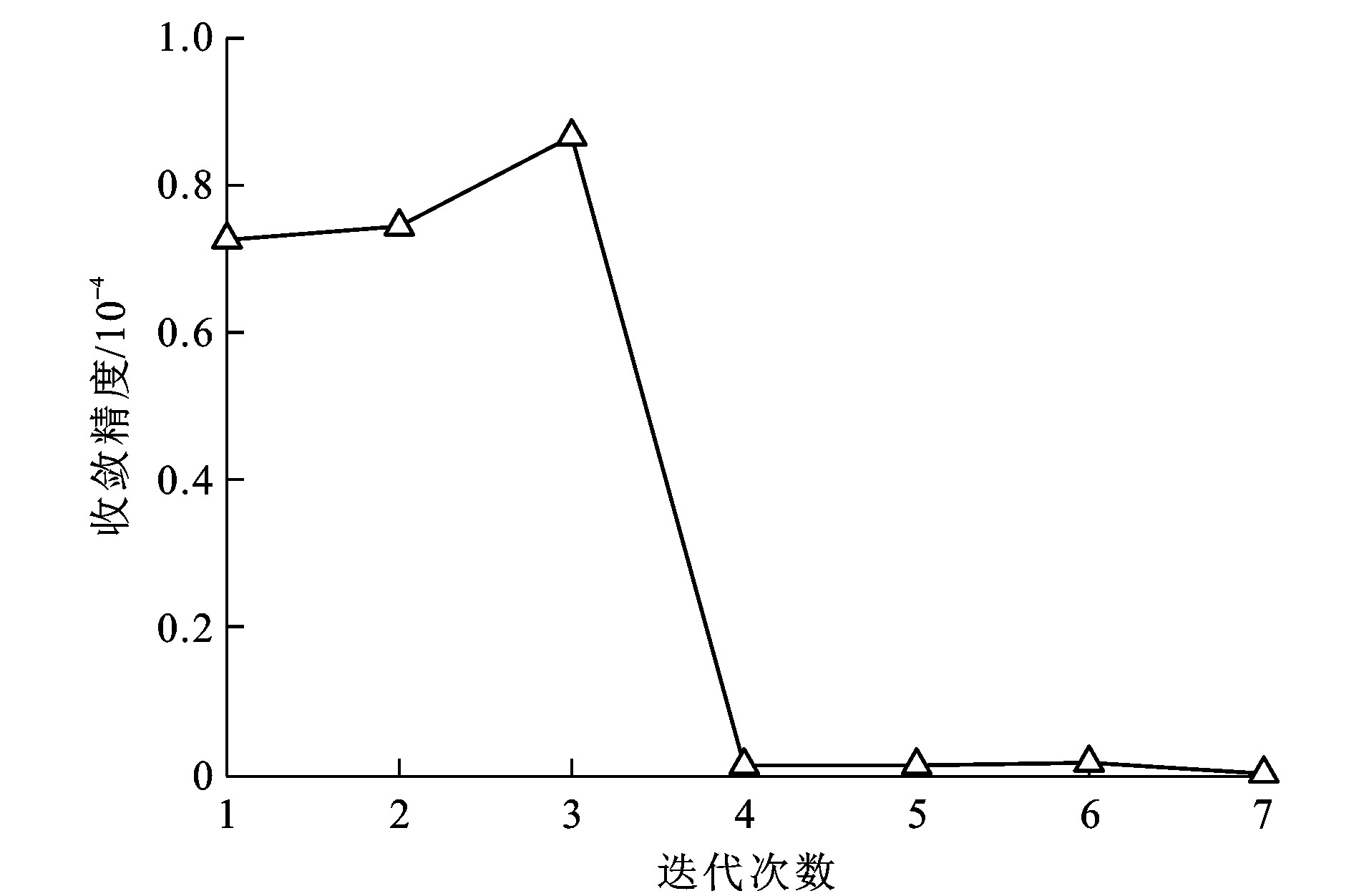
图 6为路轨两用救援车的状态概率的迭代收敛精度, 可知: 提出的矩阵压缩算法迭代7次以后, 收敛精度达到了2.589×10^-8, 且趋向于0。这说明迭代结果已趋向稳定, 故算法具有较高的求解效率。

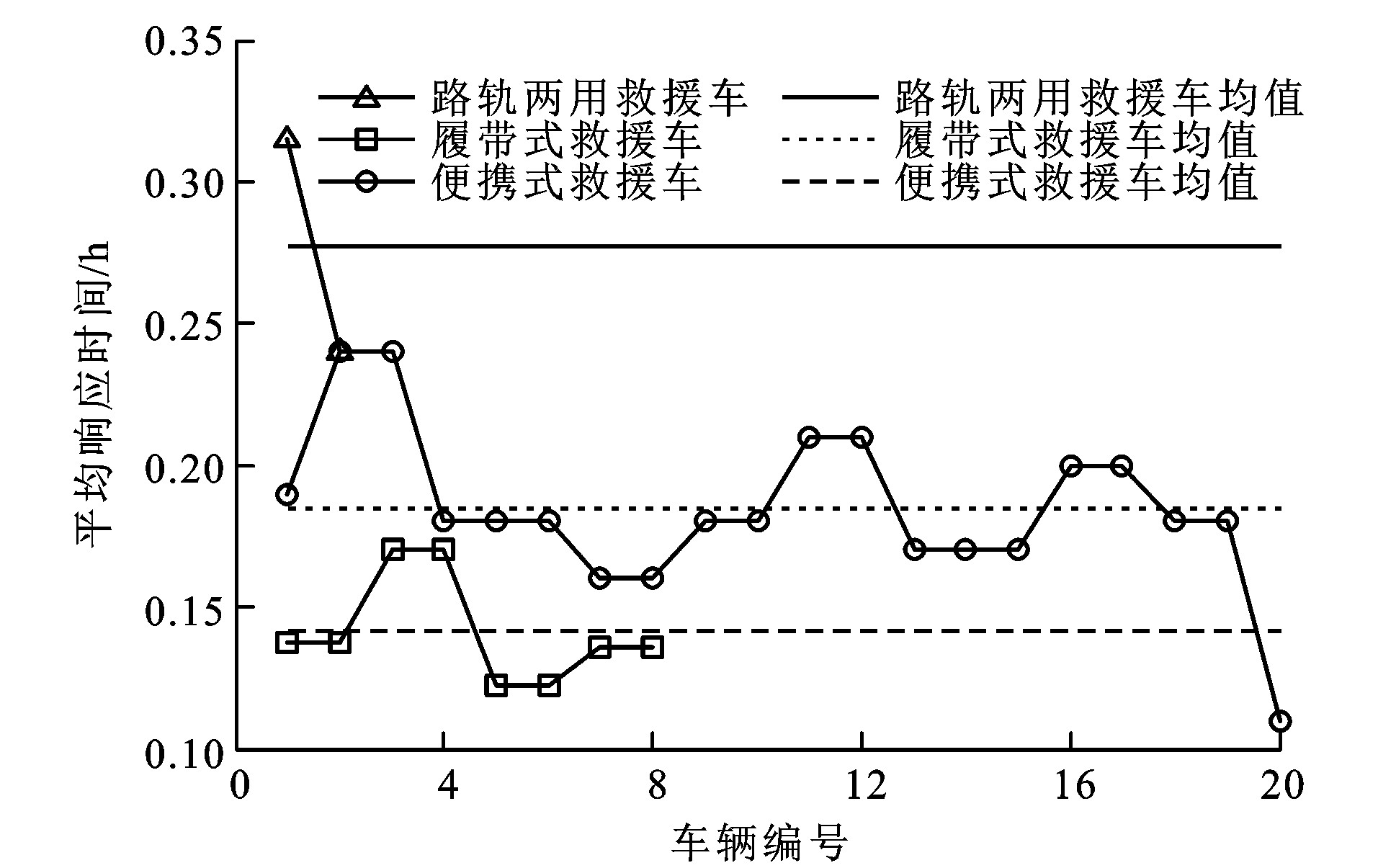
表  1  救援车辆配置

Table  1.  Deployment of rescue vehicles veh

线路	小区	车型数量
		路轨两用救援车	履带式救援车	便携式救援车
1号线	1	0	2	1
	2	0	0	2
	3	0	0	3
	4	0	0	2
	5	1	2	2
5号线	6	0	2	2
	7	0	0	2
	8	0	0	3
	9	0	0	2
	10	1	2	1

下载: 导出CSV 

| 显示表格

表  2  2007~2014年北京市地铁救援次数与时间

Table  2.  Railway rescue times and time of Beijing during 2007-2014

年份	每年救援次数		平均救援时间/min
	1号线	5号线
2007	2	2	23.0
2008	2	1	24.7
2009	2	1	47.5
2010	2	1	30.0
2011	3	0	16.3
2012	2	0	18.8
2013	0	2	20.0
2014	5	2	13.8

下载: 导出CSV 

| 显示表格

表  3  路轨两用救援车和履带式救援车在小区间的行程时间

Table  3.  Travel times of road-rail rescue vehicles and crawler rescue vehicles between zones h

小区	1	2	3	4	5	6	7	8	9	10
1	0.08	0.18	0.34	0.48	0.61	0.99	1.14	1.29	1.14	1.02
2	0.18	0.10	0.17	0.30	0.44	0.99	1.14	1.46	1.31	1.20
3	0.34	0.17	0.07	0.14	0.27	0.82	0.97	1.27	1.24	1.13
4	0.48	0.30	0.14	0.06	0.13	0.69	0.84	1.13	1.11	1.00
5	0.61	0.44	0.27	0.13	0.07	0.55	0.70	1.00	0.98	0.86
6	0.99	0.99	0.82	0.69	0.55	0.08	0.15	0.23	0.45	0.56
7	1.14	1.14	0.97	0.84	0.70	0.15	0.07	0.15	0.30	0.41
8	1.29	1.46	1.27	1.13	1.00	0.23	0.15	0.08	0.15	0.19
9	1.14	1.31	1.24	1.11	0.98	0.45	0.30	0.15	0.07	0.11
10	1.02	1.20	1.13	1.00	0.86	0.56	0.41	0.19	0.11	0.04

下载: 导出CSV 

| 显示表格

表  4  便携式救援车在小区间的行程时间

Table  4.  Travel times of portable rescue vehicles between zones h

小区	1	2	3	4	5	6	7	8	9	10
1	0.19	0.44	0.86	1.19	1.53	0.99	1.14	1.29	1.14	1.02
2	0.44	0.24	0.42	0.76	1.09	0.99	1.14	1.46	1.31	1.20
3	0.86	0.42	0.18	0.34	0.67	0.82	0.97	1.27	1.24	1.13
4	1.19	0.76	0.34	0.16	0.33	0.69	0.84	1.13	1.11	1.00
5	1.53	1.09	0.67	0.33	0.18	0.55	0.70	1.00	0.98	0.86
6	0.99	0.99	0.82	0.69	0.55	0.21	0.38	0.58	1.12	1.40
7	1.14	1.14	0.97	0.84	0.70	0.38	0.17	0.37	0.74	1.03
8	1.29	1.46	1.27	1.13	1.00	0.58	0.37	0.20	0.38	0.48
9	1.14	1.31	1.24	1.11	0.98	1.12	0.74	0.38	0.18	0.28
10	1.02	1.20	1.13	1.00	0.86	1.40	1.03	0.48	0.28	0.11

下载: 导出CSV 

| 显示表格

图  6  状态概率精度迭代收敛曲线

Figure  6.  Iterative convergence curve of state probability precision

下载: 全尺寸图片 幻灯片

图  7  救援车辆平均响应时间

Figure  7.  Mean response times of rescue vehicles

下载: 全尺寸图片 幻灯片

地铁救援的关键在于救援车辆的响应时间, 即车辆接到救援指令后达到事发地点的时间。一般各类救援系统均有响应时间要求。例如, 公安部2006年颁布的《110报警服务工作规范化标准》明确要求“凡危及公民人身、财产安全的重大、紧急报警、求助, 在市区, 必须5 min内到达现场; 在郊区, 必须10 min内到达现场。”对此, 地铁消防救援也需要类似的强制性响应时间标准。此外, 在地铁线网不同位置的乘客获得救援的响应时间还应尽量相当, 各救援车辆工作强度也应尽量平衡; 否则, 小区车辆配置将不匹配于地铁火灾发生分布, 由此既产生救援车辆的闲置, 又导致分布在地铁线网上的乘客获救机会不等。图 7为3类救援车辆的响应时间。布置在小区5的路轨两用救援车负责救援的区段较布置在小区10的路轨两用救援车要远, 模型计算结果显示前者的平均响应时间较后者的要长; 另外, 对同一救援区段配置的履带式和便携式救援车, 其响应时间是相等的。这些结果表明, 本文的模型能反映救援车辆的空间分布对救援响应时间的影响。根据图 7可知: 便携式救援车平均响应时间约为14 min, 路轨两用救援车平均响应时间约为20 min, 而履带式救援车平均响应时间约为10 min。履带式救援车具有最快的响应时间, 原因在于其兼具数量和速度优势。

图  8  救援车辆工作强度

Figure  8.  Workloads of rescue vehicles

下载: 全尺寸图片 幻灯片

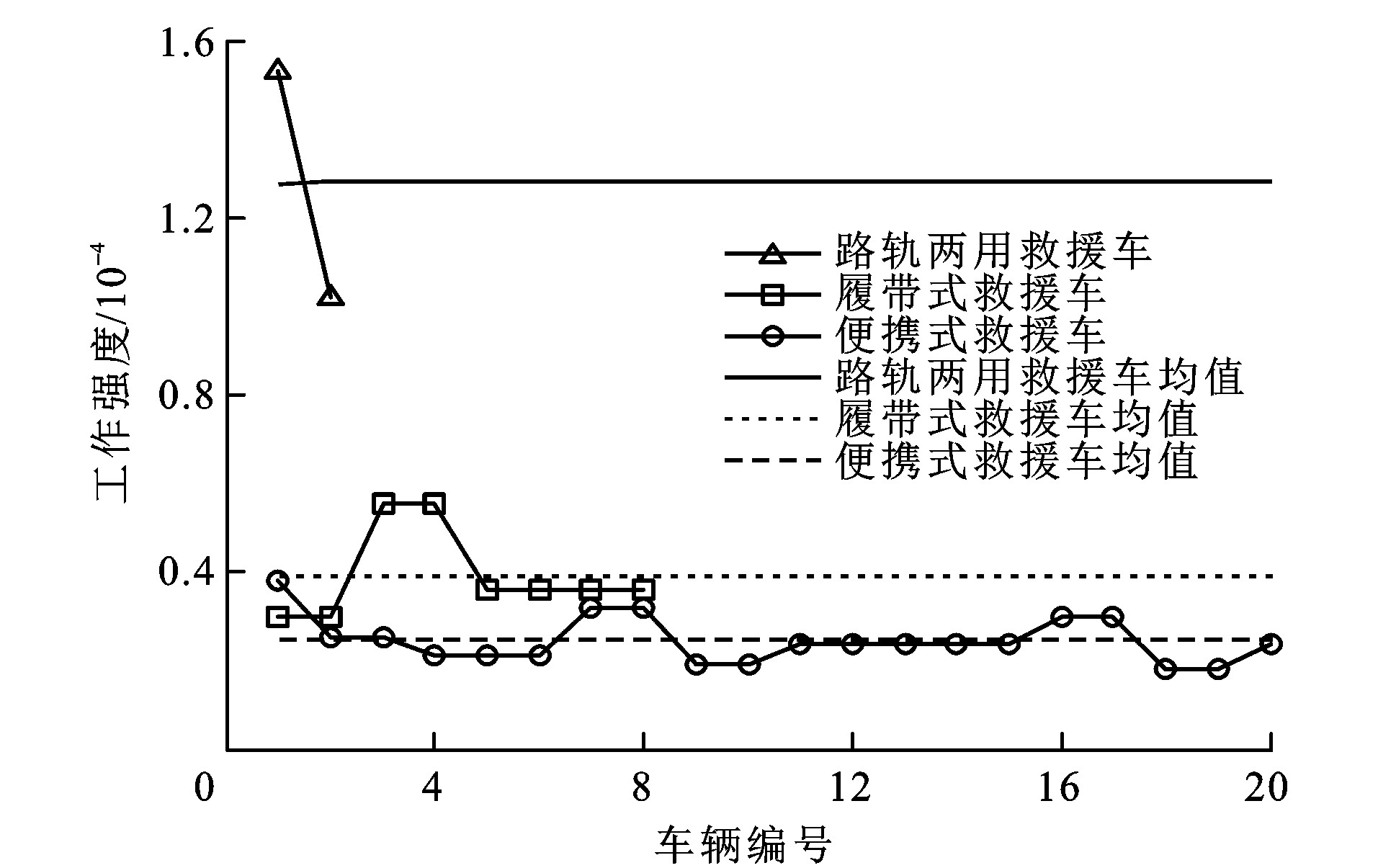
地铁救援系统规划应尽量避免救援车辆工作强度(即救援车辆处于救援时间的概率) 不均衡。图 8给出的是3类救援车辆的工作强度情况。根据图 8, 3类救援车辆在工作强度及救援强度的均衡性方面, 路轨两用救援车、履带式救援车、便携式救援车依次减小。这表明, 随着配车数量的增加, 各型救援车的救援工作强度降低, 工作强度也逐步均衡。此外, 根据图 8, 路轨两用救援车工作强度差异较大, 应该考虑增配路轨两用救援车以分担路轨1号车辆的救援强度。通过工作强度的分析可知, 采购数量较多的便携式救援车辆, 在空间上较为均匀地配置地铁救援车辆, 将在很大程度上分摊每辆救援车的工作强度。这在一定程度上印证了“不应将鸡蛋放在一个篮子里面”, 即在地铁救援时应尽可能分散救援工作强度。

图  9  路轨两用救援车与履带式救援车跨小区救援概率

Figure  9.  Cross-district rescue probabilities of road-rail rescue vehicles and crawler rescue vehicles

下载: 全尺寸图片 幻灯片

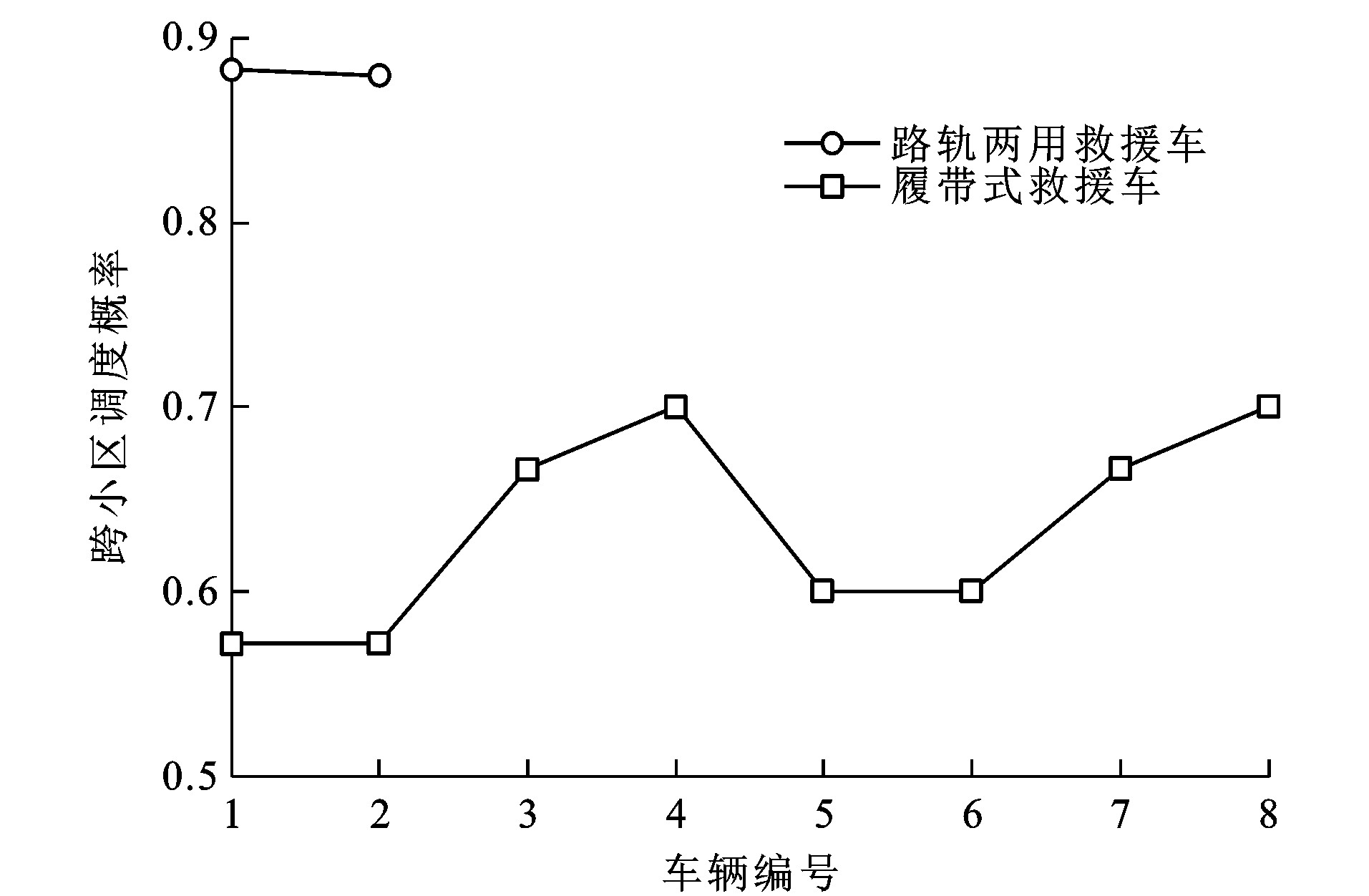
地铁救援车辆跨小区救援将增加地铁救援的响应时间, 迫使救援车配置数量增加, 因此, 应要求地铁救援系统规划尽量减少跨小区调度, 这就要求对地铁救援系统的跨小区调度进行评估计算。图 9为路轨两用救援车与履带式救援车跨小区救援概率, 图 10为便携式救援车跨小区救援概率。根据图 9可得: 2辆路轨两用救援车平均跨小区救援概率均在0.85以上; 履带式救援车的跨小区救援概率约为0.65, 其原因在于当救援车数量较少时, 无法确保每个小区有足够的救援车响应本小区救援需求, 此时只能从别的小区指派车辆进行救援。而在图 10中, 相较于履带式救援车, 由于便携式救援车其各区车辆配备充足, 跨区救援概率整体较小, 2~10号便携式救援车的跨区救援概率相对较高, 但是整体上其指派概率数量级为10^-5, 可以近似视为0, 因此, 救援车辆的数量对跨小区救援的指派影响巨大。可以发现: 在科学布置救援车的前提下, 救援车辆数量越多, 其跨小区救援概率越小, 这对于缩短救援响应时间具有重要作用。

图  10  便携式救援车跨小区救援概率

Figure  10.  Cross-district rescue probabilities of portable rescue vehicles

下载: 全尺寸图片 幻灯片

图  11  各小区利用路轨两用救援车与履带式救援车获得救援的概率

Figure  11.  Rescue probabilities of each zone obtained by using road-rail rescue vehicles and crawler rescue vehicles

下载: 全尺寸图片 幻灯片

图  12  各小区利用便携式救援车获得救援的概率

Figure  12.  Rescue probability of each zone obtained by using portable rescue vehicles

下载: 全尺寸图片 幻灯片

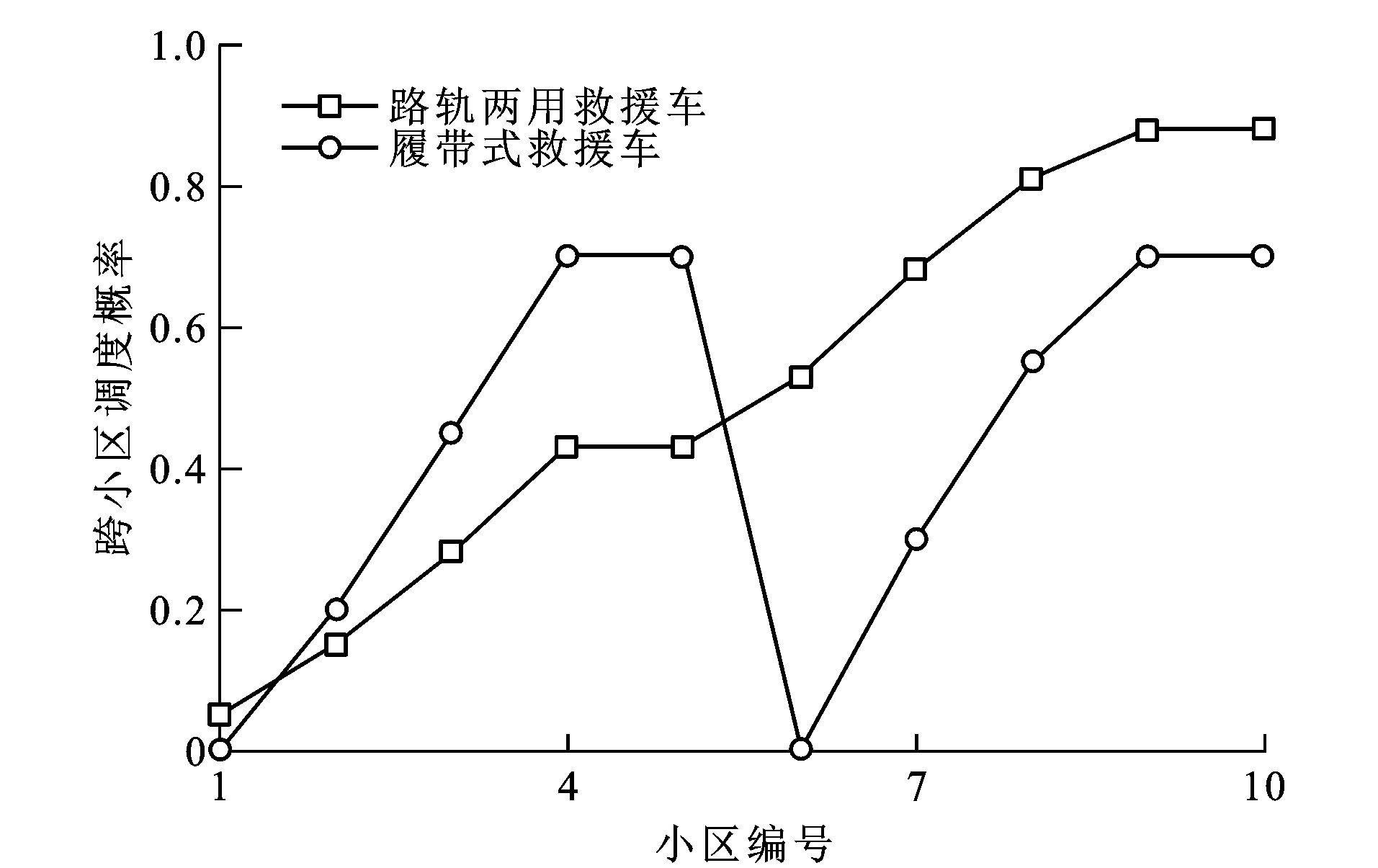
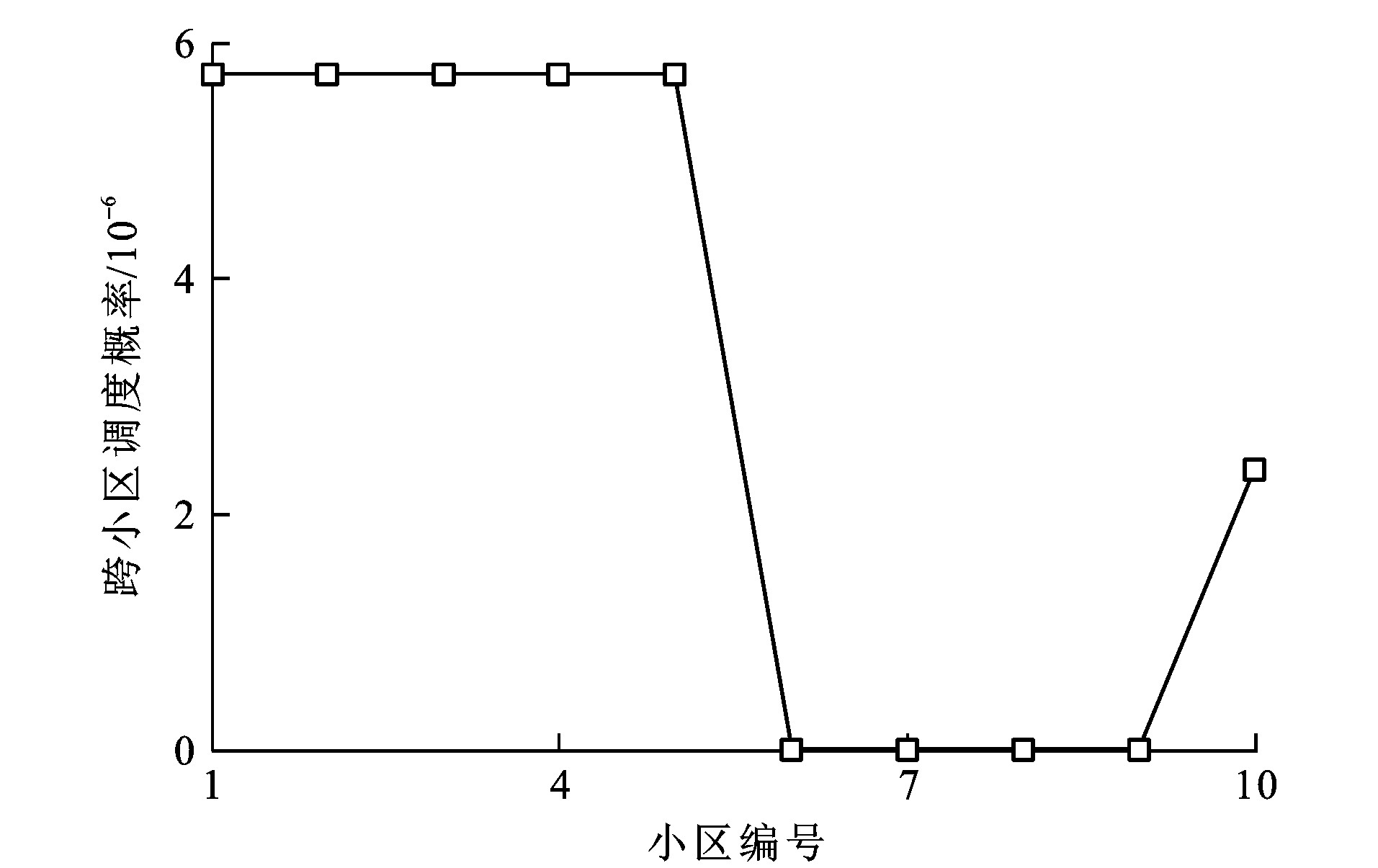
各个救援小区如果发生救援请求, 响应的救援车辆也需要来自其他小区的跨小区救援。与图 9、10不同的是, 图 11、12分别给出了各个救援小区利用路轨两用救援车与履带式救援车、便携式救援车从别的小区获得救援的概率。由图 11可知: 路轨两用救援车和履带式救援车在多个小区的跨区救援概率都很高, 达到了0.7, 而图 12中的便携式救援车的跨区救援概率数量级为10^-6, 可以近似视为0。可以看到: 在使用便携式救援车的情况下, 相较于其他2种车型, 其在各小区的车辆配备充足, 基本不需要进行跨区救援。

通过以上结果的分析可知, 在购置成本有限的条件下, 如果不考虑救援能力的差异, 无论是救援车辆工作强度、跨区救援概率, 还是小区的跨区救援概率方面, 便携式救援车的综合表现好于其他2种车; 虽然便携式救援车平均出行时间稍大于履带式救援车, 但差距很小。在购置成本一定的情况下, 其不仅可以满足各小区的配备需求, 救援速度方面也表现良好, 是三者中最佳的选择。

4.   结语

(1) 通过分析地铁灾害事故发生时各救援车辆响应救援的指派过程, 基于生灭过程建立了救援车辆状态平衡的线性方程组, 通过求解该线性方程组即可得到地铁救援车辆状态概率。由于方程组的未知数与救援车辆数量呈指数关系, 求解过程中需要巨大的动态存储空间及运算量, 为此提出了基于稀疏矩阵压缩的求解算法以减少运算量。

(2) 以实际的地铁线网为例, 经过7次迭代即可达到10^-8的求解精度, 因此, 本文提出的模型具有较高的求解效率, 所求解得到的救援车辆状态空间概率可以进一步计算救援车辆响应时间、救援服务强度、跨区救援概率等多个评价指标。

(3) 本文讨论了地铁救援车辆的配置方案与评价, 未来可以针对地铁救援系统的救援小区划分, 以救援车辆分区分布数量作为决策变量, 寻求地铁救援系统规划的最优方案。另外, 本研究假定1次地铁灾害事故仅派出1辆救援车辆, 并未考虑指派多辆救援车辆的情形。实际中, 地铁一旦发生严重的灾害事故, 往往会同时指派多辆救援车辆进行救援, 该情形值得下一步深入研究。