双向双车道超车行为的智能车队间隙控制优化

陈俊杰; 蔡伯根; 上官伟; 王剑; 柴琳果

doi:10.19818/j.cnki.1671-1637.2019.02.016

双向双车道超车行为的智能车队间隙控制优化

doi: 10.19818/j.cnki.1671-1637.2019.02.016

陈俊杰^{1, 2,},
蔡伯根^{1, 2, 3,},
上官伟^{1, 2, 3,},
王剑^{1, 2, 3},
柴琳果^{1, 2}

1.
北京交通大学电子信息工程学院, 北京 100044
2.
北京交通大学北京市轨道交通电磁兼容与卫星导航工程技术研究中心, 北京 100044
3.
北京交通大学轨道交通控制与安全国家重点实验室, 北京 100044

基金项目:

国家重点研发计划项目 2018YFB1600600

中央高校基本科研业务费专项资金项目 2018YJS019

国家自然科学基金项目 61773049

国家自然科学基金项目 61490705

详细信息

作者简介:
陈俊杰(1989-), 男, 河北沧州人, 北京交通大学工学博士研究生, 从事车路协同自主车辆群体智能控制与优化技术研究

蔡伯根(1966-), 男, 江苏南通人, 北京交通大学教授, 工学博士

通讯作者:
上官伟(1979-), 男, 陕西乾县人, 北京交通大学教授, 工学博士

中图分类号: U491.51
计量
- 文章访问数: 1257
- HTML全文浏览量: 225
- PDF下载量: 538
- 被引次数: 12
出版历程
- 收稿日期: 2018-11-03
- 刊出日期: 2019-04-25

Slot control optimization of intelligent platoon for dual-lane two-way overtaking behavior

CHEN Jun-jie^{1, 2
,},
CAI Bo-gen^{1, 2, 3
,},
SHANGGUAN Wei^{1, 2, 3
,},
WANG Jian^{1, 2, 3},
CHAI Lin-guo^{1, 2}

1.
School of Electronics and Information Engineering, Beijing Jiaotong University, Beijing 100044, China
2.
Beijing Engineering Research Center of EMC and GNSS Technology for Rail Transportation, Beijing Jiaotong University, Beijing 100044, China
3.
State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China

More Information

Author Bio:
CHEN Jun-jie (1989-), male, doctoral student, junjiechen@bjtu.edu.cn

CAI Bai-gen (1966-), male, professor, PhD, bgcai@bjtu.edu.cn

SHANGGUAN Wei (1979-), male, professor, PhD, wshg@bjtu.edu.cn

Article Text (Baidu Translation)

摘要

摘要: 建立了双向双车道环境下单车超越车队模型, 分析了影响双向双车道超车危险区域范围的主要因素; 设计了分步式单车超越车队算法, 研究了安全间隙前后车速度、超车车辆入队速度与车队安全间隙范围四者之间的关系, 提出了车辆入队所需最小安全间隙的速度匹配方案; 建立了单车超越车队算法的目标函数, 设定最大允许超车时间内超车车辆与车队行驶距离最大, 超车车辆超越车队车辆数最多, 前、后车形成安全间隙过程中加速度、减速度最小; 提出了基于改进粒子群的分级约束多目标优化方法, 为单车超越车队算法中的三级车速引导提供了优化的速度引导方案。研究结果表明: 双向双车道环境下超车危险区域范围与车队车辆数及对向车辆行驶速度成正相关关系; 改进的粒子群优化算法相比传统算法具有更强的鲁棒性和更快的收敛速度, 平均收敛时间缩短39.2%;在分步式单车超越车队过程中, 车队车辆平均速度提升9.04%, 即在车队间隙生成过程中, 虽然部分车辆速度减小, 但车队整体平均速度得到提升; 超车车辆平均速度提升16.8%, 即在超车过程中, 不仅超车车辆的安全性得到保证, 其运行效率也得到提升。
- 交通信息工程 /
- 双向双车道 /
- 智能车队 /
- 单车超越车队算法 /
- 安全间隙 /
- 间隙优化 /
- 分步式超车
Abstract: A model of single vehicle overtaking a platoon on the dual-lane two-way road was established, and the key factors affecting the range of dangerous overtaking zone were analyzed. The step-by-step algorithm was designed when single vehicle overtakes the platoon. The relationship among the speeds of the vehicles before and after the safety slot, the speed of the overtaking vehicle entering the platoon and the safety slot range of the platoon was studied. The speed matching scheme with the minimum safety slot required for the vehicle to overtake the platoon was proposed. The objective function of the algorithm was established, and the following assumptions were made in the maximum allowable overtaking time: the overtaking vehicle and platoon travelled the longest distance, the overtaking vehicle overtaked the platoon by the most vehicles, and the acceleration and deceleration of front and rear vehicles were the minimum in the forming process of safety slot. The hierarchical constrained multi-objective optimization method based on the improved particle swarm was proposed to provide the algorithm with the optimized three-level speed guidance strategy. Analysis result shows that the overtaking dangerous zone on dual-lane two-way road is positively correlated with the number of vehicles in the platoon and the velocities of the opposite vehicles. The improved particle swarm optimization algorithm has stronger robustness and faster convergence than the traditional algorithm, and the average convergence time reduces by 39.2%. In the step-by-step process that the single vehicle overtakes the platoon, the average speed of the vehicles in the platoon increase by 9.04%, which means that in the forming process of safety slot, although the speeds of some vehicles decrease, the overall average speed of the platoon increases. The average speed of overtaking vehicle increases by 16.8%, which means that in the overtaking process, not only is the safety of overtaking vehicle guaranteed, but also its operating efficiency is improved.
- traffic information engineering /
- dual-lane two-way road /
- intelligent platoon /
- algorithm of single vehicle overtaking platoon /
- safety slot /
- slot optimization /
- step-by-step overtaking

HTML全文

0. 引言

双向双车道是中国公路网中最普通的公路形式之一, 西部地区双向双车道公路占公路总里程的95%以上, 在公路网中发挥着重要的作用。智能车队组队运行是提升双向双车道典型道路交通效率的重要手段, 面临着车辆与车队间的超车-放弃两难问题, 迫切需要深入开展其组队行为分析与编组优化方法研究。

车辆超车行为涉及到的因素包括超车车辆、被超车辆、道路, 双向双车道环境下还包括对向车辆, 因此, 需要建立超车车辆从超车开始到超车完成所需超车视距的模型^{[1, 2, 3]}, 超车车辆包括道路上行驶的所有机动车辆。许伦辉等依据车辆运行特性对超车车辆进行分类, 考虑不同道路等级的设计时速, 建立了计算超车车辆从超车行为发生到超车过程结束所需的超车时间和距离的数学模型^[4]。超车行为发生的道路包括双车道公路和多车道公路, Cheng等运用所采集的数据分析了多车道车辆换道行为, 提出车辆换道方式和频率与道路交通状况等因素有关^[5]。双车道公路上, 车辆超车必须占用对向车道, 且只能在对向车道有足够的超车视距时才有变换车道进行超车的可能, 否则必须保持跟驰行驶状态^{[6, 7]}。超车需求随着交通量的增加而增加, 而进入对向车道伺机超车的能力却在降低, 荣建等对中国标准二级双车道的双向通行能力进行仿真试验^[8]。

超车过程是与换道行为紧密联系的, 超车是驾驶人换道行为的主要动机, 为研究驾驶人换道特性, 党睿娜等在分析驾驶人接近前车行为决策的基础上, 研究了换道阶段的车辆、车间状态变化和换道操作习惯^[9]; 王畅等对换道决策阶段驾驶人对后方车辆的速度感知特征进行了研究, 采用显著性分析方法, 分析了相对速度、后方车辆速度与相对距离对驾驶人速度估计行为的影响特性^[10]。车辆超车换道包括超车时的加速换道和超车车辆的归位换道, 徐磊等对超车换道可行域进行了动态构建, 对换道边界轨迹进行规划, 依据期望跟车距离和安全碰撞条件确定可行域的上、下边界, 并依据两车的运动关系确定超车换道条件^[11]。车辆换道归位时, 超车车速与原车道车速, 车间距以及道路限速有关, 柏伟等对不同限速条件下的超车模型进行了研究, 为车辆的超车条件提供了判断指标^[12]; 熊晓夏等提出了基于贝叶斯因子阈值法的隐马尔可夫模型和基于运动时间窗特征提取法的支持向量机模型, 预测危险换道驾驶行为^[13]。

超车换道在一定程度上能够提高道路利用率, 针对未来车路协同环境所提供的车辆交互基础信息, 李珣等提出了一种考虑局部区域车辆状态优化的协同换道模型^[14]; Milanés等开发了一种基于模糊逻辑的控制器, 通过输入由来自视觉系统、全球定位系统和惯性测量单元组成的基于定位的系统信息, 输出方向盘, 油门和制动踏板等车辆执行器上的动作来模拟超车过程^[15]。

目前, 对于车辆超车行为的研究, 主要集中在车辆超越车辆以及车辆超越由无车车通信的多车辆组合而成的车队方面^{[16, 17, 18]}, 而对于车辆超越具有车车通信^[19]的群体智能车队却少有研究, 部分学者对理想状态下单车超越车队的必要消息应答方式做了研究^{[20, 21, 22, 23]}, 但并没有对超车时车队内部车辆间距的控制以及超车车辆返回原车道时的限制条件进行研究。实际上, 在双向双车道中进行车辆对车队的超车行为时, 一旦驾驶人对对向来车的距离以及车队长度产生误判, 车辆很容易陷入一种既不能完成超车又不能返回原车道的危险区域^{[24, 25, 26]}, 致使超车车辆与对向车辆被迫紧急停车或相撞, 或超车车辆强行并入原车道车队, 从而与车队车辆相撞。同时, 像青藏公路等担负主要物资运输任务的双向双车道, 大车结队行驶具有队列长, 队列多, 行驶速度快的特点^{[27, 28, 29]}, 上述车辆对运输车队的超车缺陷会更加明显。

本文通过建立单车超越车队运动学模型, 从理论上分析、论证了双向双车道路段, 车辆对车队超车时“超车-放弃”两难的危险区域是确实存在的, 并通过模型确定了与危险区域影响因素; 研究了超车车辆在完成超车动作或放弃超车后返回原车道时车速和车队安全间隙的关系; 最后提出了基于动态安全间隙的双向双车道分步式单车超越车队(Single Vehicle Overtaking Platoon, SVOP) 算法, 并通过设计基于改进粒子群的分级约束多目标优化方法, 为分步式超车算法中超车车辆与安全间隙前、后车的三级车速引导提供了行驶里程、超越多车数量、舒适性多目标优化方案。

1. 双向双车道SVOP模型

1.1 SVOP模型建立

在双向双车道路段, 在超车车辆占用对向车道超车的过程中, 若被超越车队中相邻车辆车头间距不足以满足超车车辆的超车要求时, 对向车道出现车辆使得视距小于安全超车视距要求, 超车车辆往往陷入超车的危险区域, 即超车车辆此时既不能超车, 又不能返回原车道。

在此定义超车车辆临界位置与临界时间, 假设当超车车辆进入超车道行驶至临界位置之前始终有机会放弃超车, 安全返回原车道, 而当超车车辆在超车道越过临界位置点后则进入超车危险区域; 超车车辆由超车开始行驶至临界位置的时间为临界时间。

安全完成超车动作, 应满足的条件为: 超车车辆与对向车辆避免碰撞; 超车车辆与被超越车队头车之间保持必要的安全距离, 单晓峰等对安全超车条件作了详细说明^[30], 为方便阐述SVOP算法的实现, 在此仅做简单说明, 如下

$\begin{array}{l} o \geq (v_{0} + v_{1}) (t_{0} + t_{1}) + J_{1} (1) \\ J_{1} = (v_{0} + v_{1}) h_{1} (2) \\ J_{2} = v_{2} h_{2} (3) \\ J_{2} + l_{1} = v_{0} (t_{0} + t_{1}) + J_{3} - \\ v_{2} (t_{0} + t_{1}) - (Ν - 1) v_{2} h_{3} (4) \end{array}$

安全超车的视距条件为

$\begin{array}{l} o_{1} \geq \frac{(v_{0} + v_{1}) {v_{2} [h_{2} + (Ν - 1) h_{3}] + l_{1} - J_{3}}}{v_{0} - v_{2}} + \\ (v_{0} - v_{1}) h_{1} (5) \end{array}$

式中: o为安全行驶视距下限; v₀为超车车辆加速后的速度; v₁为超车车辆对向车辆速度; v₂为车队速度; t₀为临界时间; t₁为临界时刻后的剩余超车过程时间; J₁为超车结束时, 超车车辆与对向车辆之间的最小安全距离; J₂为完成超车时, 超车车辆尾部与被超越车队头车的车头之间的距离; J₃为超车车辆加速后与被超越车队尾车的车头距离; h₁为J₁的安全时距; h₂为J₂的安全时距; h₃为被超越车队中车头时距; l₁为超车车长; N为车队车辆数; o₁为安全超车视距。

超车车辆在超车的过程中放弃超车, 能够安全返回原车道应满足条件为: 超车车辆返回原车道时应与对向车辆以及下游车辆之间保持一定的安全距离, 同时, 超车车辆减速返回原车道时速度不应太小, 以避免阻碍后方车辆的正常行驶。条件为

$\begin{array}{l} J_{4} = h_{4} (v_{0} - d t_{2}) = \\ v_{2} (t_{0} + t_{2}) - l_{2} - J_{3} - v_{0} t_{0} - v_{0} t_{2} + \frac{d t_{2}^{2}}{2} (6) \\ o_{2} \geq v_{0} t_{0} + v_{0} t_{2} - \frac{d t_{2}^{2}}{2} + v_{1} (t_{0} + t_{2}) + J_{5} (7) \\ J_{5} = (v_{0} - d t_{2} + v_{1}) h_{1} (8) \end{array}$

允许放弃超车的视距条件为

$\begin{array}{l} o_{2} \geq (v_{2} + v_{1} + h_{4} d) t_{2} + (v_{2} + v_{1}) t_{0} - l_{2} - \\ J_{3} - h_{4} v_{0} + (v_{0} - d t_{2} + v_{1}) h_{1} (9) \end{array}$

取o₁和o₂中较小的值作为视距条件, 即

$o = \min {o_{1}, o_{2}} (10)$

式中: J₄为超车车辆返回原车道时车头与车队尾车尾部之间的距离; h₄为J₄的安全时距; d为超车车辆减速度; t₂为放弃超车开始减速至返回原车道过程时间; l₂为车队车长; J₅为返回原车道时与对向车辆之间的最小安全距离; o₂为允许放弃超车视距。

当视距条件小于安全超车和允许放弃超车视距时, 车辆陷入超车和放弃超车的危险情况。

1.2 SVOP危险区域影响因素

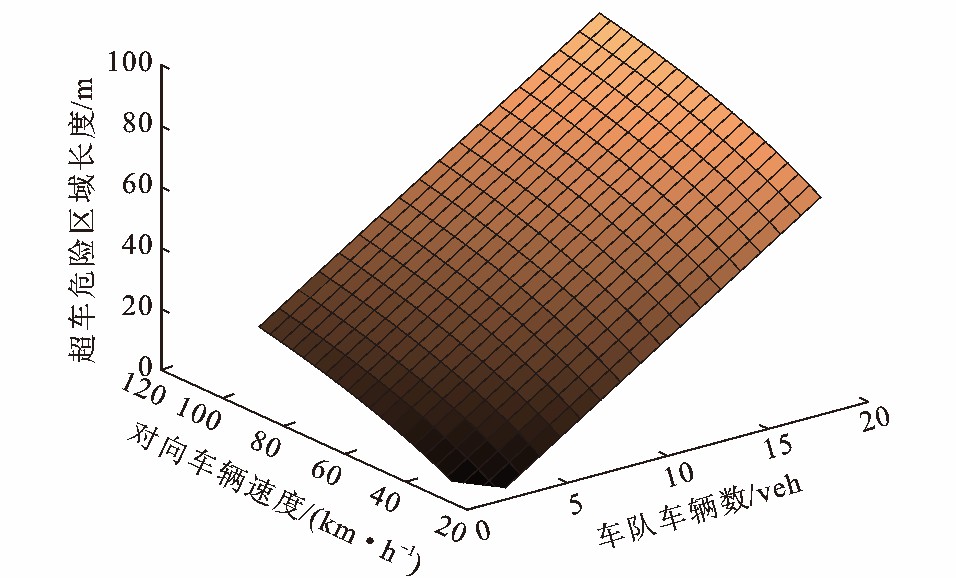
超车危险区域范围即由车队头车车头位置至超车车辆临界位置。为便于分析影响超车危险区域范围的因素, 这里假设: 完成超车时, 超车车辆尾部与被超越车队头车的车头时距为2 s; 被超越车队中车辆间车头时距为3 s; 所有车辆车长为5 m; 超车车辆返回原车道时车头与下游车辆尾部之间的安全时距为2 s; 超车车辆超车时对向车辆速度为60 km·h^-1; 超车车辆超车时加速后的车速为80 km·h^-1; 车队速度为60 km·h^-1; 超车车辆加速后与下游第1辆车的车头间距为20 m; 超车结束时, 超车车辆与对向车辆之间的最小安全时距为3 s。将由式(10) 所得临界时间t₀代入式(7)、(9) 可得超车危险区域与被超越车队车辆数和对向车辆速度的关系见图 1。

图 1 超车危险区域曲面

Figure 1. Surface plot of dangerous overtaking area

下载: 全尺寸图片幻灯片

图 2 分步式超车

Figure 2. Step-by-step overtaking

下载: 全尺寸图片幻灯片

由图 1可以看出: 超车危险区域的产生不仅与开始超车时的视距判断有关, 还与车队车辆数和对向车辆行驶速度相关, 超车危险区域随着车队车辆数的增加以及对向车辆行驶速度的增加而增大。

2. 分步式SVOP算法

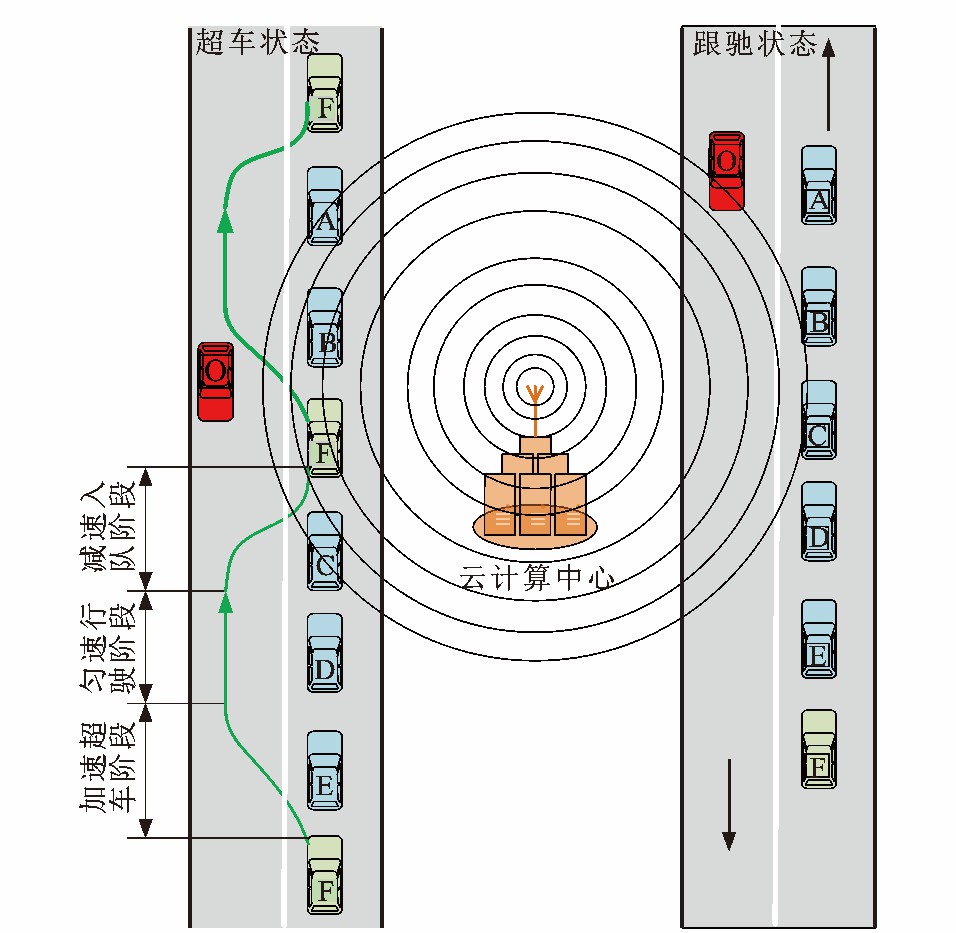
针对双向双车道中, 车辆对车队进行超车时所面临的超车-放弃两难问题, 本文提出“分步式”SVOP算法, 见图 2, A~E为车队车辆; F为超车车辆; O为对向车道行驶车辆。云计算中心负责收集路段车辆信息, 并计算最优超车方案。

超车车辆跟驰车队时, 在进行换道超车行为之前, 超车车辆需加入车队自组织网络, 车队车辆形成云计算中心以便对超车车辆的超车换道进行规划协调。

在双向双车道中, 超车车辆F超越由车辆A~E组成的车队时(车队组成车辆数并无限制), 车辆O由对向车道驶来, 为避免超车车辆进入超车危险区域, 云计算中心为超车车辆及车队车辆进行车速引导, 车辆F按照云计算中心提供的车速引导信息行驶进行超车行为, 车辆B及其前车队、车辆C及其后车队按照云计算中心提供的速度引导信息行驶并形成安全间隙以供车辆F入队(车辆B、C为云计算中心通过计算选取车辆), 车辆F首先超越车队中车辆C~E并入队, 待对向车辆O驶过之后, 车辆F按照云计算中心发布的车速引导信息行驶并超越车辆B和A, 此即分步式超车算法所要达到的车辆对车队的超车目标。

综上所述, 分步式超车算法流程如下。

Step 1:车辆提出超车申请, 云计算中心获取超车车辆、车队车辆的位置、速度、加速度、最大加速度、最大制动减速度、车辆长度等基本信息。

Step 2:等待车辆提出超车申请后, 云计算中心获取对向车辆的基本信息。

Step 3:云计算中心在回复车辆的超车申请前, 计算此时车辆进行超车行为是否存在进入超车危险区域的可能, 若不存在, 则给出车辆对整个车队进行安全超车的速度引导信息。

Step 4:若通过计算, 预测车辆将进入超车危险区域, 云计算中心选取车队中的理想位置生成安全间隙, 以供车辆完成第1步超车动作后返回原车道并入队。

Step 5:云计算中心在输出车队安全间隙前、后车以及超车车辆的“最佳车速引导信息组”后, 匹配三级车辆的最大加速度、最大制动减速度信息, 在“最佳车速引导信息组”中选取可行车速引导方案。

Step 6:车队安全间隙前、后车以及超车车辆按照云计算中心提供的车速引导信息行驶, 车辆在完成超车动作后, 向云计算中心发送单步超车完成信息。

Step 7:云计算中心在接收到超车车辆的单步超车完成信息后, 更新车队车辆, 对向车道车辆基本信息, 按照Steps 3~5为超车车辆的下一步超车进行速度引导。

可以看出, 分步式超车是由不同“单步”超车叠加的过程, 在此将分步超车的单步过程进行重点研究, 即车辆在有限的时间内借用对向车道完成对车队内的局部车辆进行超车并入队。

在执行分步式超车算法时面临2个关键技术问题: 在单步超车过程中, 如何选取车队内安全间隙的形成位置; 在单步超车结束后超车车辆入队时, 如何匹配超车车辆速度与车队内安全间隙范围。

实际上, 在选择车队内车辆入队安全间隙形成位置前, 必须解决车辆入队时, 超车车辆速度与安全间隙匹配问题。安全间隙与入队车速成正相关关系, 二者相匹配时既要满足超车过程的快速性, 即超车车辆速度不能过小, 又不能使安全间隙过大, 影响车队行驶效率。

2.1 超车车辆速度与安全间隙匹配

为了匹配入队车速与安全间隙, 本节对超车车辆与安全间隙前、后车三者之间的不同速度关系以及安全间隙之间的联系展开研究。

车辆入队时需保证超车车辆与安全间隙前、后车均处于安全跟驰状态, 为此首先研究车车跟驰时不同车速关系下的安全间距条件。

假设相距为l的2辆车, 在同一车道上沿同一方向行驶, 跟驰车辆和前向车辆行驶速度分别为v₃、v₄, 驶过的距离分别为L₀和L₁, 最大的制动减速度分别为a₀和a₁, 驾驶人反应时间为t₃, 减速度的增长时间为t₄, 车辆停止后跟驰车辆与前向车辆之间的安全距离为H。跟驰车辆与前向车辆有如下3种速度关系。

(1) 跟驰车辆速度大于前向车辆速度

跟驰车辆在前向车辆制动后, 驾驶人经过反应时间t₃才开始减速, 跟驰车辆行驶的距离为

$L_{0} = v_{3} t_{3} + \frac{v_{3}^{2}}{2 a_{0}} + v_{3} t_{4} - \frac{1}{2} a_{0} t_{4} (11)$

前向车辆在有准备的情况下做匀减速运动, 驾驶人不需要反应时间, 则前向车制动距离为

$L_{1} = \frac{v_{4}^{2}}{2 a_{1}} + v_{4} t_{4} - \frac{1}{2} a_{1} t_{4} (12)$

跟驰车辆和前向车辆之间的安全跟驰距离为

$\begin{array}{l} Η_{1} = v_{3} t_{3} + \frac{v_{3}^{2}}{2 a_{0}} - \frac{v_{1}^{2}}{2 a_{1}} + (v_{3} - v_{4}) t_{4} + \\ \frac{(a_{1} - a_{0}) t_{4}}{2} + l (13) \end{array}$

(2) 跟驰车辆速度等于前向车辆速度

当跟驰车速等于前向车速时, 即v₀=v₁=v, 跟驰车辆与前向车辆的安全跟驰距离为

$Η_{2} = v t_{3} + v^{2} (\frac{1}{2 a_{0}} - \frac{1}{2 a_{1}}) + \frac{(a_{1} - a_{0}) t_{4}}{2} + l (14)$

(3) 跟驰车辆速度小于前向车辆速度

当跟驰车辆速度小于前向车辆速度时, 跟驰相对安全。当前向车辆减速至跟驰车辆速度时, 跟驰车辆必须进行减速操作才能保证安全行驶。前向车辆减速至跟驰车辆车速所需的时间t₅为

$t_{5} = t_{4} + \frac{v_{4} - v_{3} - a_{1} t_{4} / 2}{a_{1}} (15)$

在t₅时间段内, 跟驰车辆行驶距离s₁为

$s_{1} = v_{3} t_{4} + \frac{v_{3} (v_{4} - v_{3} - a_{1} t_{4} / 2)}{a_{1}} (16)$

当前向车辆减速至跟驰车辆速度时, 跟驰车辆必须采取减速操作, 此过程中跟驰车辆行驶距离s₂为

$s_{2} = v_{3} t_{3} + \frac{v_{3}^{2}}{2 a_{0}} + v_{3} t_{4} - \frac{a_{0} t_{4}}{2} (17)$

跟驰车辆总的行驶距离为

$L_{0} = s_{1} + s_{2} (18)$

由于前向车辆进行有准备的减速行驶, 不需要反应时间, 所以前向车辆行驶距离同式(11) 中的L₁, 两车的安全跟驰距离H为

$\begin{array}{l} Η = v_{3} (t_{3} + t_{4}) + \frac{2 v_{3} v_{4} - 2 v_{3}^{2} - v_{3} a_{1} t_{4} - v_{4}^{2}}{2 a_{1}} + \\ \frac{v_{3}^{2}}{2 a_{0}} + (v_{3} - v_{4} + \frac{a_{1} - a_{0}}{2}) t_{4} + l (19) \end{array}$

由式(13) ~ (19) 可以得出: 当跟驰车速等于前向车速时, 实际为跟驰车速小于前向车速的极限情况, 即式(14) 为式(13) 在 $\lim_{v_{3} \to v_{4}} (v_{3} - v_{4}) = 0$ 的特定情况。综上, 在车辆跟驰行为中, 跟驰车辆与前向车辆的速度关系可分为2种, 即跟驰车速小于等于前向车速或跟驰车速大于前向车速。当超车车辆完成换道超车动作后返回原车道时, 超车车辆速度v₅、前车速度v₆与后车速度v₇三者之间的速度关系满足表 1。

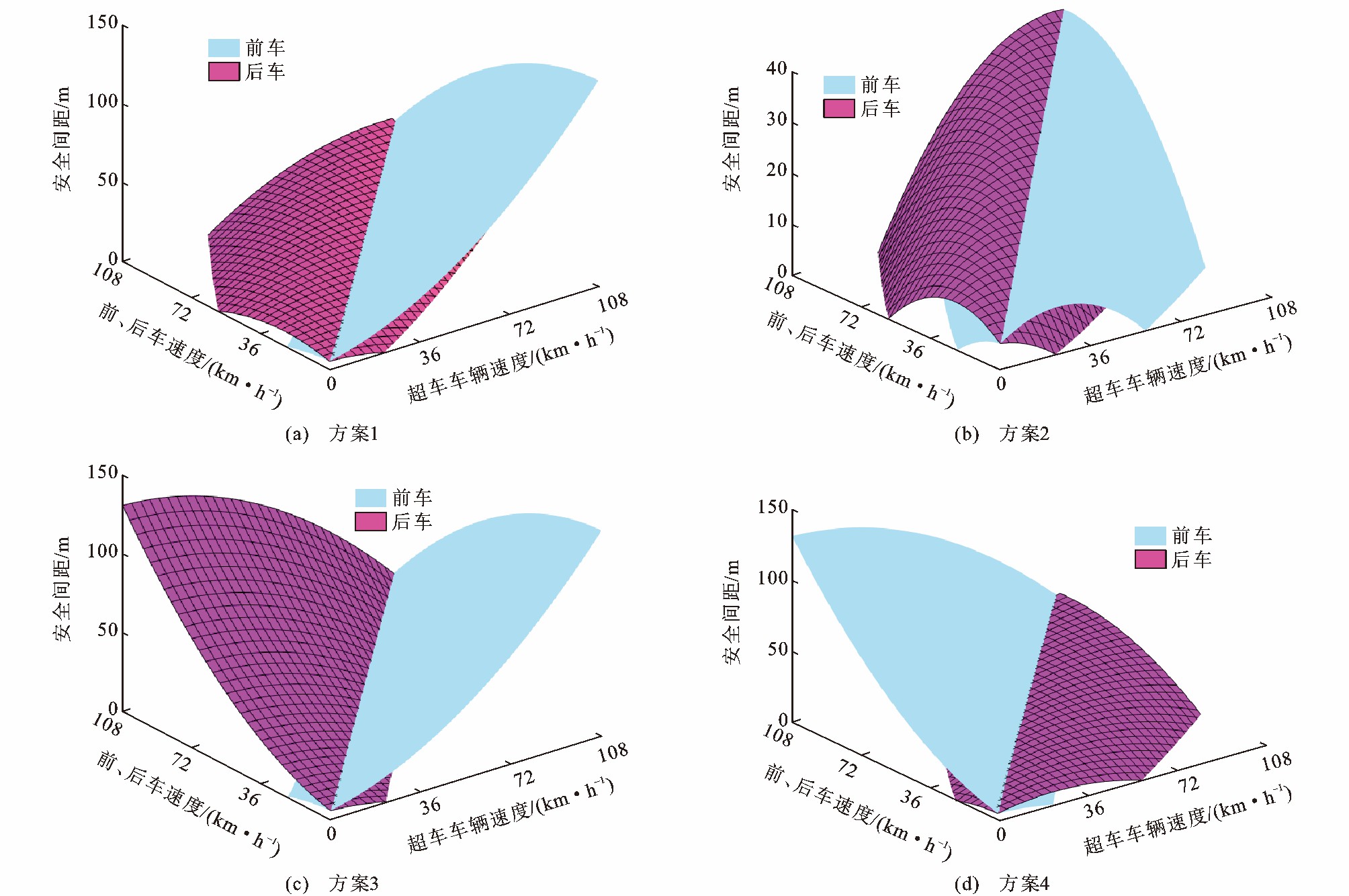
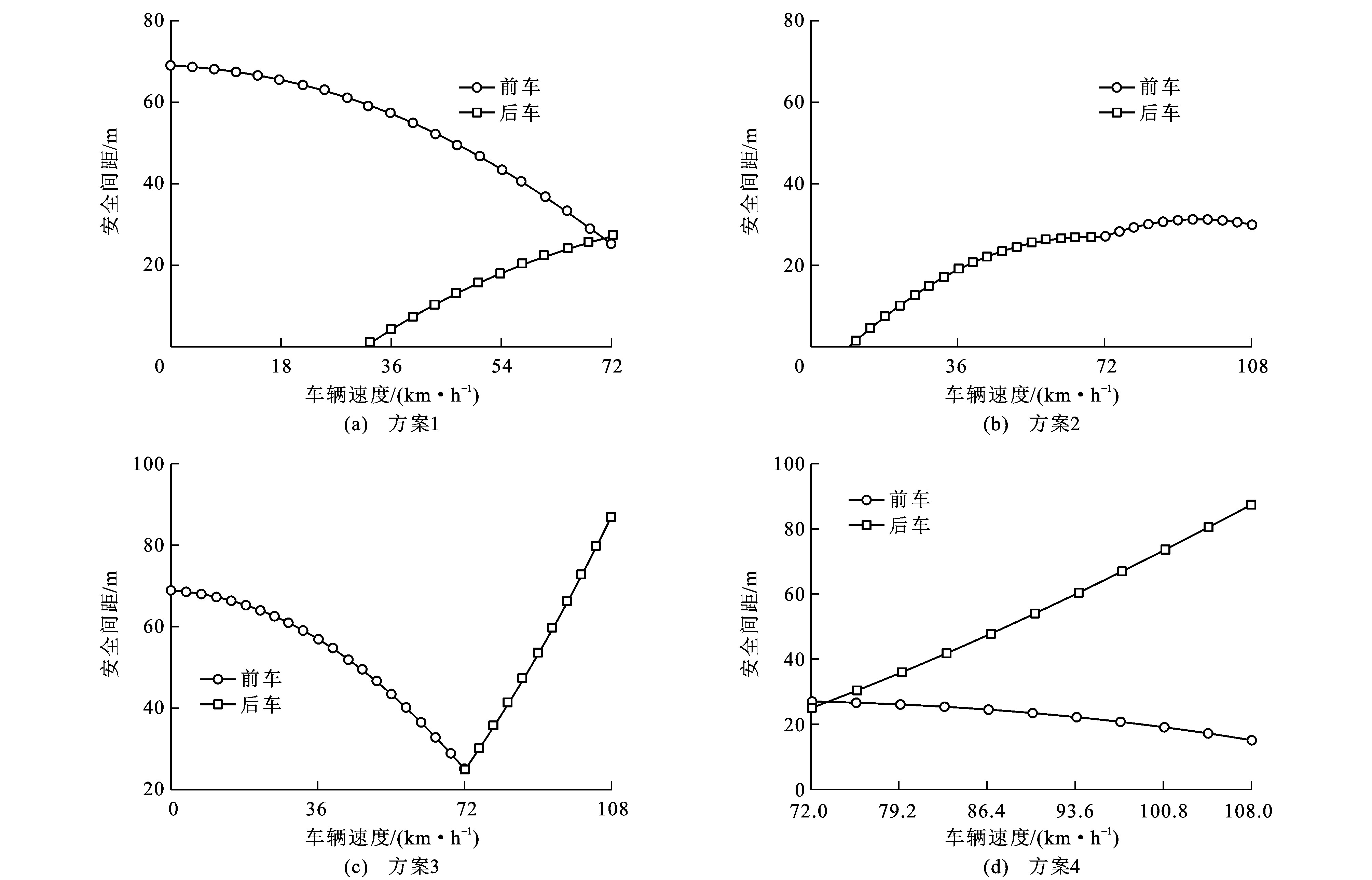
表 1 v₅~v₇关系

Table 1. Relationship among v₅, v₆and v₇

方案	v₅与v₆关系	v₅与v₇关系	图示
1	v₅ > v₆	v₅ > v₇	3 (a)
2	v₅≤v₆	v₅ > v₇	3 (b)
3	v₅ > v₆	v₅≤ v₇	3 (c)
4	v₅≤v₆	v₅≤v₇	3 (d)

下载: 导出CSV

| 显示表格

图 3 不同车速关系条件下安全间距分布

Figure 3. Safety distance distributions under different velocity relationships

下载: 全尺寸图片幻灯片

针对车辆超越车队中部分车辆后返回原车道场景, 本文对超车车辆、前车与后车三者的不同速度关系组合与安全间距之间的联系展开研究。

图 3(a)~(c)中右侧曲面为超车车辆与安全间隙前车之间不同的速度匹配与安全间距的关系, 左侧曲面为超车车辆与安全间隙后车之间不同的速度匹配与安全间距的关系, 图 3(d)中左侧曲面为超车车辆与安全间隙前车之间不同的速度匹配与安全间距的关系, 右侧曲面为超车车辆与安全间隙后车之间不同的速度匹配与安全间距的关系。

超车车辆入队时, 车队内安全间隙需大于2段安全跟驰间距(超车车辆与安全间隙前车安全跟驰间距、超车车辆与安全间隙后车安全跟驰间距) 与车长之和; 安全间隙前车速度与安全间隙后车速度的设定需考虑形成最小安全间隙的需求。

2.2 车队安全间隙位置选取

在分步式超车过程中, 安全间隙位置的择优选取是另一个关键问题, 在选择形成安全间隙的相邻车辆时, 要充分考虑安全间隙与超车车辆入队速度的匹配。

设定双向双车道路段限速为v₈; 超车车辆最大加速度为a₂; 超车加速时间为t₆; 车辆超车时, 被选择的安全间隙前车加速时间为t₇; 被选择的安全间隙后车减速时间为t₈; 超车车辆入队时减速时间为t₉; 超车过程时间为t₁₀; 车队车辆速度为v′_k (k=1, 2, 3, …, N); 最大加速度为a₃; 最大减速度为a₄; 车队中相邻车辆车头时距为t₁₁; 车辆超车时与对向车辆间距为s₃; 超车车辆在第1步超车过程中超过车队车辆数为n; 超车车辆入队时减速度为a₅。默认对向车辆车速恒定。

超车过程时间上限为

$\begin{array}{l} t_{10} \leq \frac{s_{3} + a_{2} t_{6}^{2} / 2}{v_{0} + a_{2} t_{6} + v_{1}} (20) \\ {\begin{matrix} t_{10} < \frac{s_{3}}{v_{1} + v_{0}} \\ t_{10} \geq \frac{\sqrt{(v_{1} + v_{0})^{2} + 2 a_{2} s_{3}} - v_{1} - v_{0}}{a_{2}} \end{matrix} (21) \end{array}$

在t₁₀时间内, 超车车辆的行驶距离S₁为

$\begin{array}{l} S_{1} = v_{0} t_{6} + \frac{a_{2} t_{6}^{2}}{2} + (v_{0} + a_{2} t_{6}) (t_{10} - t_{6} - t_{9}) + \\ (v_{0} + a_{2} t_{6}) t_{4} - \frac{a_{5} t_{9}^{2}}{2} (22) \end{array}$

安全间隙前车在t₁₀内行驶的距离S₂为

$S_{2} = v^{'}_{n + 1} t_{7} + \frac{a_{3} t_{7}^{2}}{2} + (v^{'}_{n + 1} + a_{3} t_{7}) (t_{10} - t_{7}) (23)$

安全间隙后车在t₁₀内行驶的距离S₃为

$S_{3} = v^{'}_{n} t_{8} - \frac{a_{4} t_{8}^{2}}{2} + (v^{'}_{n} - a_{4} t_{8}) (t_{10} - t_{8}) (24)$

在最大允许超车时间内以超车车辆及车队车辆行驶里程最大, 超车车辆超越车队内车辆数最多, 安全间隙前、后车形成安全间隙过程中加、减速度最小为目标, 并充分考虑在超车过程中道路限速条件与车辆入队时的安全间距条件, 给出满足超越条件的车辆入队位置与三级车速引导信息。在分步式超车过程中, 单步最优目标函数分别为

约束条件为

${\begin{matrix} v_{8} \geq v^{'}_{k} \\ v_{0} + a_{2} t_{6} \leq v_{8} \\ v^{'}_{k + 1} + a_{3} t_{7} \leq v_{8} \\ S_{1} - S_{3} - v^{'}_{k} n t_{6} \geq Η \\ S_{2} - S_{1} + v^{'}_{k} (n + 1) t_{11} - l_{1} \geq L_{1} \\ t_{6}, t_{7}, t_{8} \leq \frac{s_{3}}{v_{1} + v_{0}} \end{matrix} (26)$

本文在多目标优化过程中采用约束法, 同时由于粒子群算法对被优化函数的连续性要求低, 需要调整的参数少, 收敛速度快, 在Pareto解集形成过程中采用改进的粒子群寻优算法。

设搜索空间为B维, 种群粒子数为M, 每个粒子表示为一个B维向量, 其中第i个粒子表示为x_i= (x_i1, x_i2, …, x_ib, …, x_iB), 每个粒子的位置就是一个潜在的解, 将x_i代入一个目标函数就可以算出其适应值, 根据适应值的大小衡量解的优劣。粒子在t时刻的飞行速度为v_i (t) = (v_i1 (t), v_i2 (t), …, v_ib (t), …, v_iB (t)), 粒子截止到t时刻搜索到的最优位置为p_iB (t) = (p_i1 (t), p_i2 (t), …, p_ib (t), …, p_iB (t)), 粒子群截止到t时刻搜索到的最优位置为p_B (t) = (p₁ (t), p₂ (t), …, p_b (t), …, p_B (t))。迭代过程为

$\begin{array}{l} v_{i b} (t + 1) = v_{i b} (t) + c_{1} r_{1} [p_{i b} (t) - x_{i b} (t)] + \\ c_{2} r_{2} [p_{b} (t) - x_{i b} (t)] (27) \\ x_{i b} (t + 1) = x_{i b} (t) + v_{i b} (t + 1) (28) \end{array}$

式中: c₁、c₂分别为调节粒子飞向自身和全局最好位置方向的步长; r₁、r₂为相互独立的伪随机数, 服从[0, 1]上的均匀分布。i∈[1, M], b∈[1, B]; 学习因子c₁和c₂为非负常数; v_ib (t) ∈[-v_max, v_max], v_max为最大速度, 是一个常数, 可根据具体需求设定。

设置较大的c₁值, 会使微粒过多地在局部范围内徘徊, 而较大的c₂值, 则又会促使微粒过早收敛到局部最小值。为了有效地控制微粒的飞行速度, 使算法达到全局探测与局部开采两者间的有效平衡, 本文构造了引入外收缩因子与内收缩因子的粒子群优化(Particle Swarm Optimization, PSO) 算法, 这种调整方法通过选取合适的参数, 可确保PSO算法的收敛性, 并可取消对速度的边界限制。速度为

$\begin{array}{l} v_{i b} (t + 1) = φ {v_{i b} (t) + α [c_{1} r_{1} (p_{i b} (t) - x_{i b} (t)) + \\ c_{2} r_{2} (p_{b} (t) - x_{i b} (t))]} (29) \\ φ = \frac{2}{2 - c - \sqrt{c^{2} - 4 c}} (30) \\ c = c_{1} + c_{2} > 4 \\ α = \frac{w - y}{w - y} (31) \\ w = \frac{\sum_{i = 1}^{Μ} \sqrt{\sum_{b = 1}^{B} [p_{i b} (t) - \bar{p}_{b} (t)]^{2}}}{\ln [Μ π z^{2} / 4]} (32) \end{array}$

式中: φ为外收缩因子; α为内收缩因子; y为种群多样性下限; w为种群多样性系数; $\bar{p}_{b}$ 为粒子第b个分量的平均值; z为粒子向量中取值范围最大的分量的全距。

分级约束多目标优化方法是根据每个目标在具体事件中的影响力不同, 将多个目标进行分级, 选择优先级最高的参考目标, 如f₀ (x)、…、f_η (x)、…、f_ε (x), 按优先级由高到低进行排列, η代表第η优先级, η越小优先级越高, ε为重点优化目标个数, m为总的优化目标个数, 而要求其他m-ε个目标函数满足一定的约束要求。

这里求得的最优解是原多目标优化问题的Pareto弱有效解x。约束法重点保证前ε个目标的效益, 同时又适当照顾其他目标。

超车的目的是提高行驶效率, 在同等的时间里尽最大可能行驶最远的路程, 在此, 以车辆行驶最大里程为首选优化目标, 即

$\begin{array}{l} \max Ο_{1} = v_{0} t_{6} + \frac{a_{2} t_{6}^{2} - a_{5} t_{9}^{2}}{2} + \\ (v_{0} + a_{2} t_{6}) (t_{10} - t_{6}) (33) \end{array}$

在分步式超车过程中, 只有车辆超越车队中尽可能多的车辆, 才可能在下一步的超车过程中完成对整个车队的超越, 在此, 以车辆在超车过程中超越车队内尽可能多的车辆数为次优化目标, 即

min O₂=max0, S₁-max (v₀nt₁₁+S₃) (34)

云计算中心确定安全间隙形成位置后, 需要对车队车辆行驶状态进行优化, 使安全间隙范围既满足超车车辆入队条件又不至浪费间隙资源, 增加车队车辆行驶压力, 同时避免车队车辆行驶顿化, 在此, 以车队安全间隙前、后车的加速度变化量最小为优化目标。

多目标优化方法步骤如下。

Step 1:初始化一个规模为1 000的种群, 设定初始位置、速度、学习因子与种群多样性下限。

(1) 对群体中的任意粒子i, 在搜索空间内服从均匀分配产生x_i。

(2) 设定v_max=1, 对任意粒子i, 在[-v_max, v_max]内服从均匀分布, 并产生v_i。

(3) 学习因子c₁和c₂初始设定为经验值1.496 18。

(4) 种群多样性下限为0.001。

Step 2:计算每个粒子的适应值。

Step 3:将每个粒子的适应值和其经历过的最好位置的适应值进行比较, 若较好, 则将其作为当前的最好位置。

Step 4:将每个粒子的适应值和全局经历过的最好位置的适应值进行比较, 若较好, 则将其作为当前的全局最好位置。

Step 5:根据式(28)、(29), 分别对粒子的位置和速度进行更新。

Step 6:如果满足终止条件, 则输出结果; 否则回到Step 2。

Step 7:将输出结果按目标优先级由高到低进行排列, 得到Pareto解集。

3. 仿真结果分析

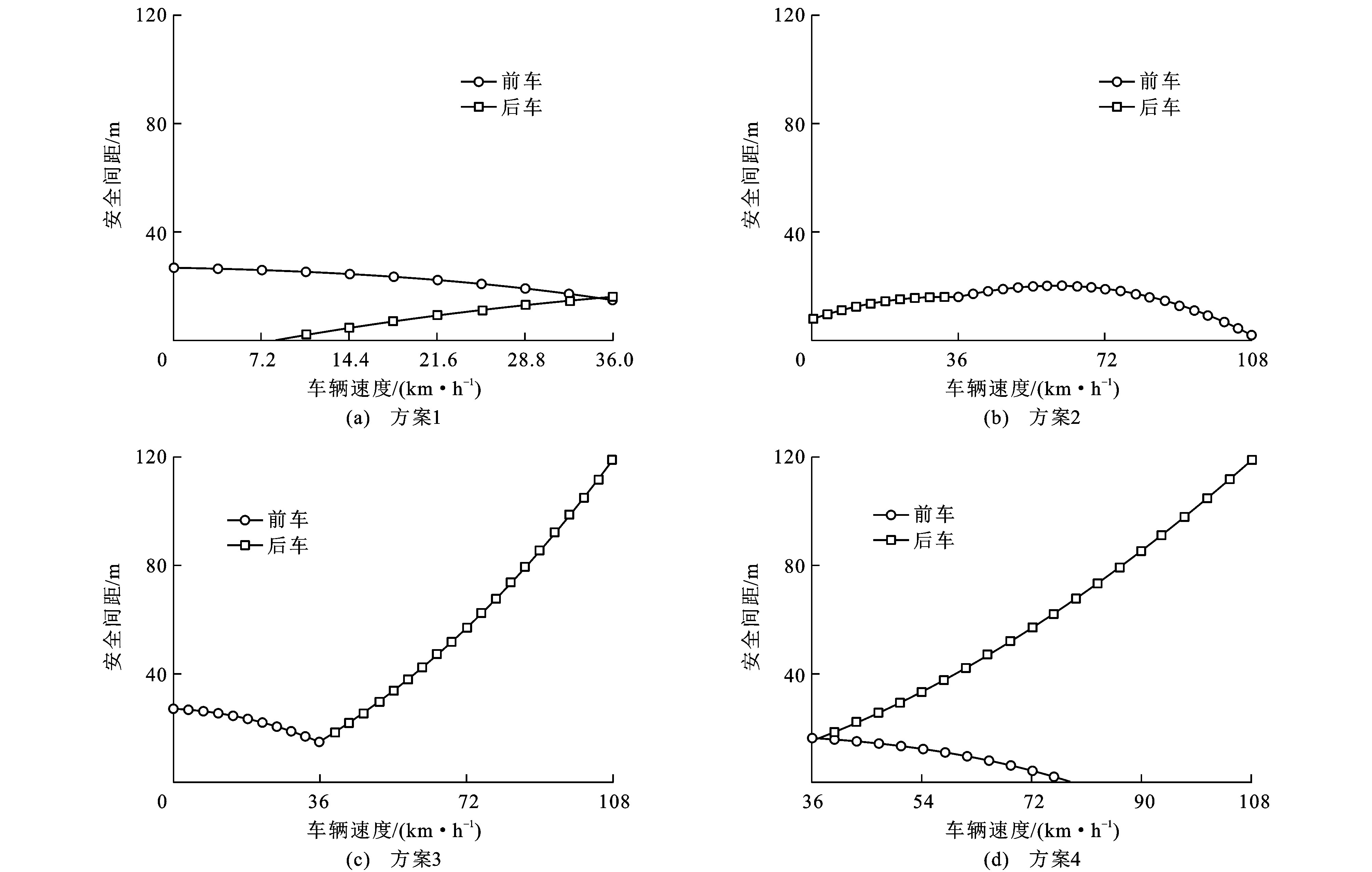
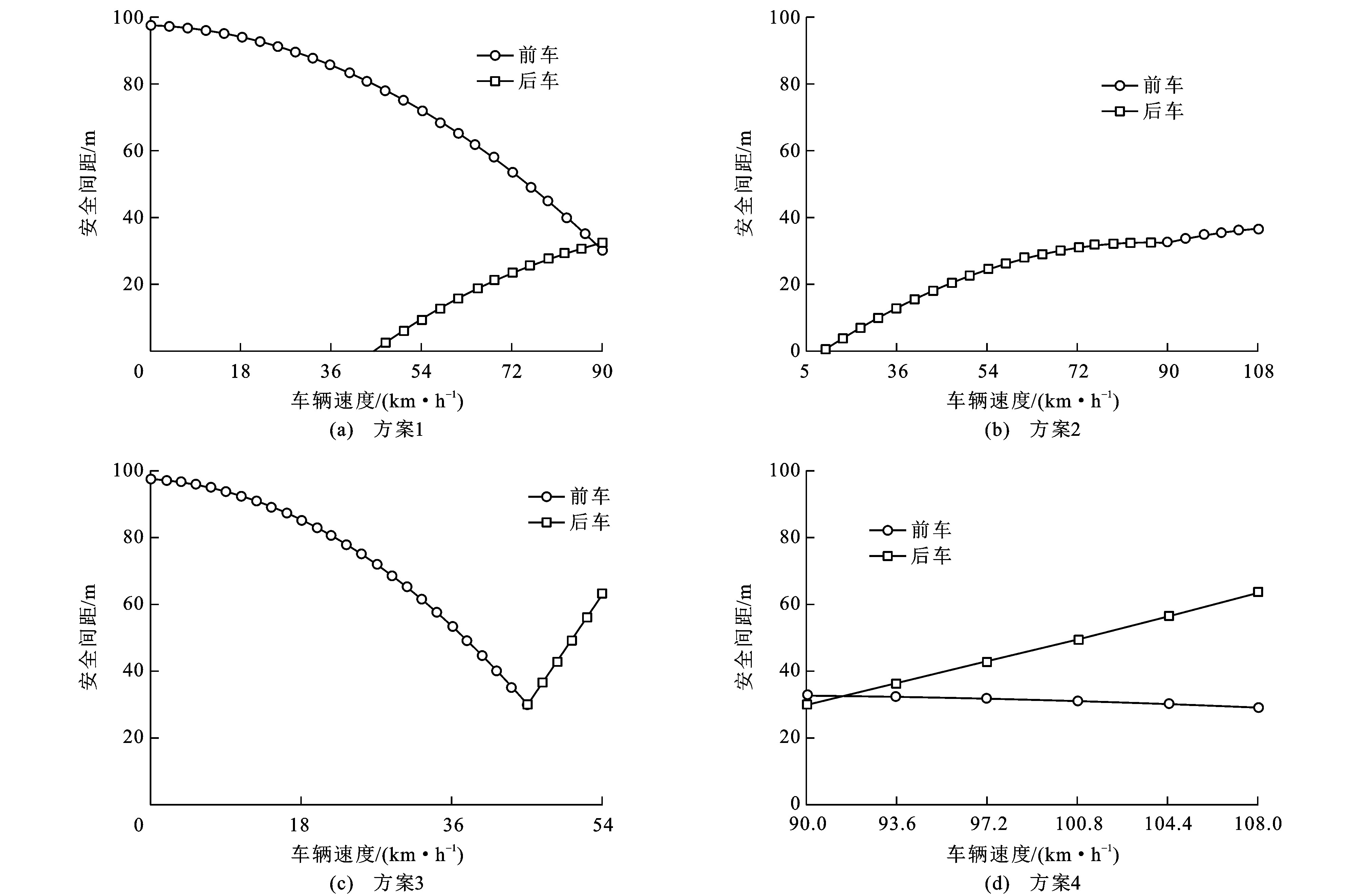
设定参数见表 2。在相同的车辆入队车速条件下, 为了选取表 1所列4种车速关系中安全间隙最小的组合, 设定车辆入队速度分别为36、72、90 km·h^-1, 对4种情况下超车车辆与安全间隙前、后车三者的不同速度组合与安全间隙关系进行剖析。

表 2 分步式超车仿真参数

Table 2. Simulation parameters of step-by-step overtaking

参数	数值
s₃/m	600
H/m	0.5
l₁、l₂/m	5
N/veh	30
a₂/ (m·s^-2)	4
a₃/ (m·s^-2)	4
a₄/ (m·s^-2)	7
v₀/ (m·s^-1)	12
v′k/ (m·s^-1)	10
v₁/ (m·s^-1)	10
t₃/s	1
t₄/s	0.2
t₁₁/s	3

下载: 导出CSV

| 显示表格

图 4~6分别对应超车车辆在不同入队车速条件下, 表 1所列4种关系下的安全入队间距与其前、后车辆速度之间的关系, 其中: 方案1中超车车辆跟驰安全间隙前车时所需的安全间距、方案3中超车车辆跟驰安全间隙前车和超车车辆与安全间隙后车的安全间距、方案4中超车车辆与安全间隙后车的安全间距都存在特定速度区间内所需安全间距过大的情况, 唯有方案2中车辆入队所需安全间距平稳且较小。

综上, 超车车辆入队时, 最佳速度关系为超车车辆速度大于安全间隙后车速度, 同时小于安全间隙前车速度。

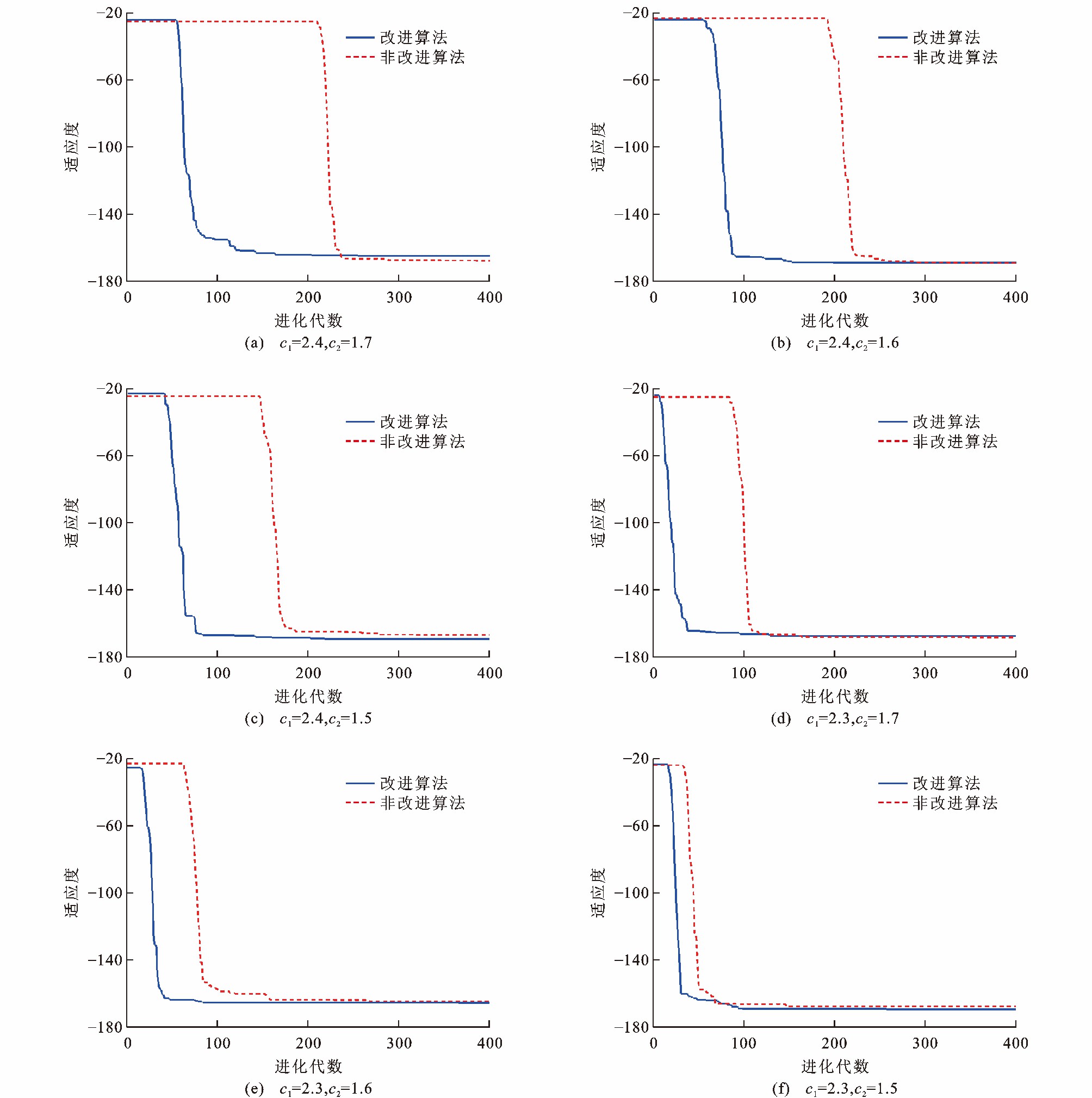
调整学习因子c₁和c₂为不同组合, 对非改进粒子群算法和改进粒子群算法的仿真结果进行对比, 通过图 7可以看出: 改进后的粒子群优化算法在不同学习因子参数下均优于传统粒子群优化算法, 鲁棒性更强; 学习因子设定为c₁=2.3, c₂=1.5时(图 7 (f)), 种群平均收敛代数最少, 即收敛速度最快。此时相比于非改进粒子群优化算法, 收敛时间缩短39.2%。

图 4 超车车速为36 km·h^-1时前、后车速与安全间距关系曲线

Figure 4. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 36 km·h^-1

下载: 全尺寸图片幻灯片

图 5 超车车速为72 km·h^-1时前、后车速与安全间距关系曲线

Figure 5. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 72 km·h^-1

下载: 全尺寸图片幻灯片

图 6 超车车速为90 km·h^-1时前、后车速与安全间距关系曲线

Figure 6. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 90 km·h^-1

下载: 全尺寸图片幻灯片

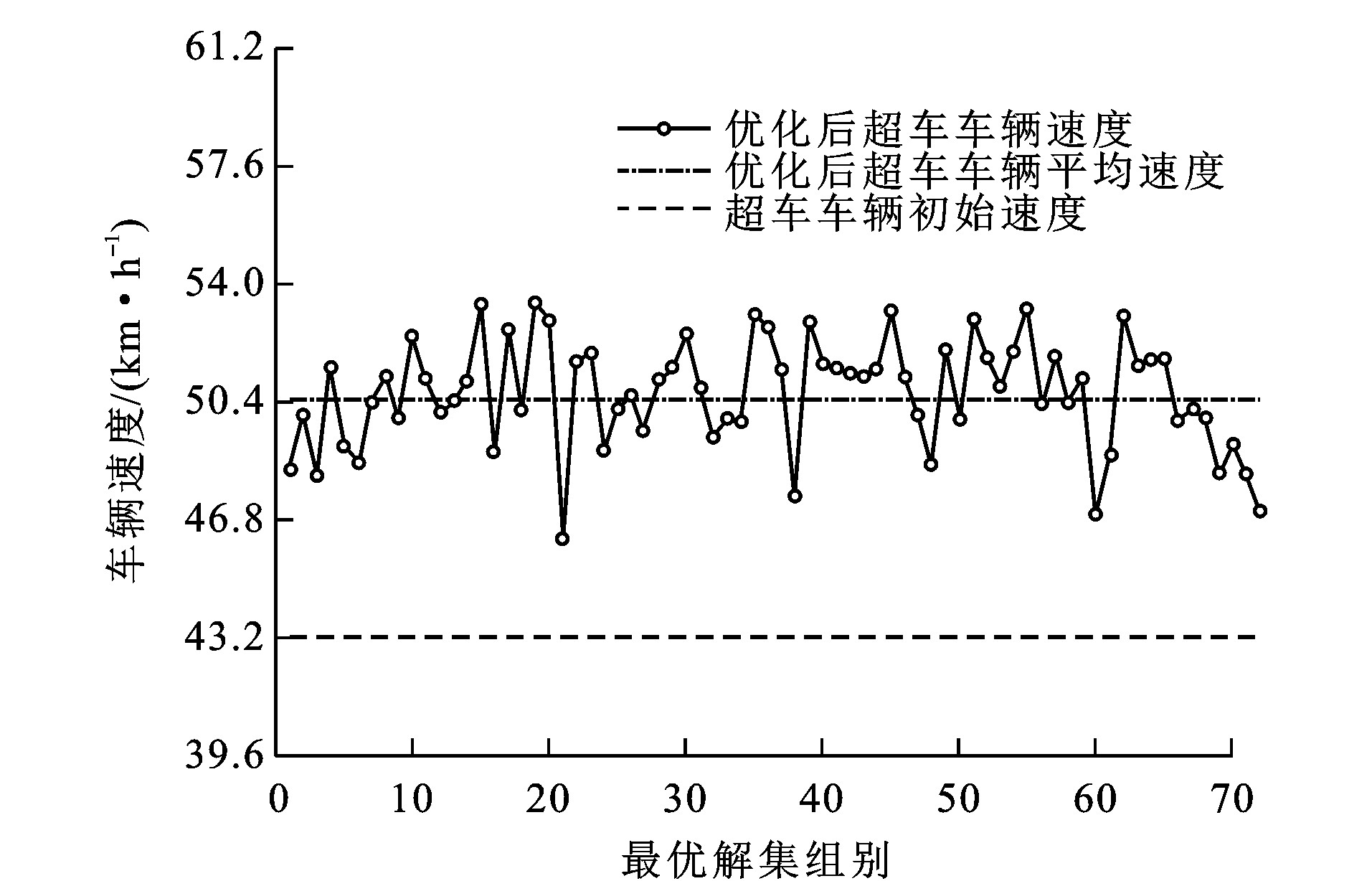
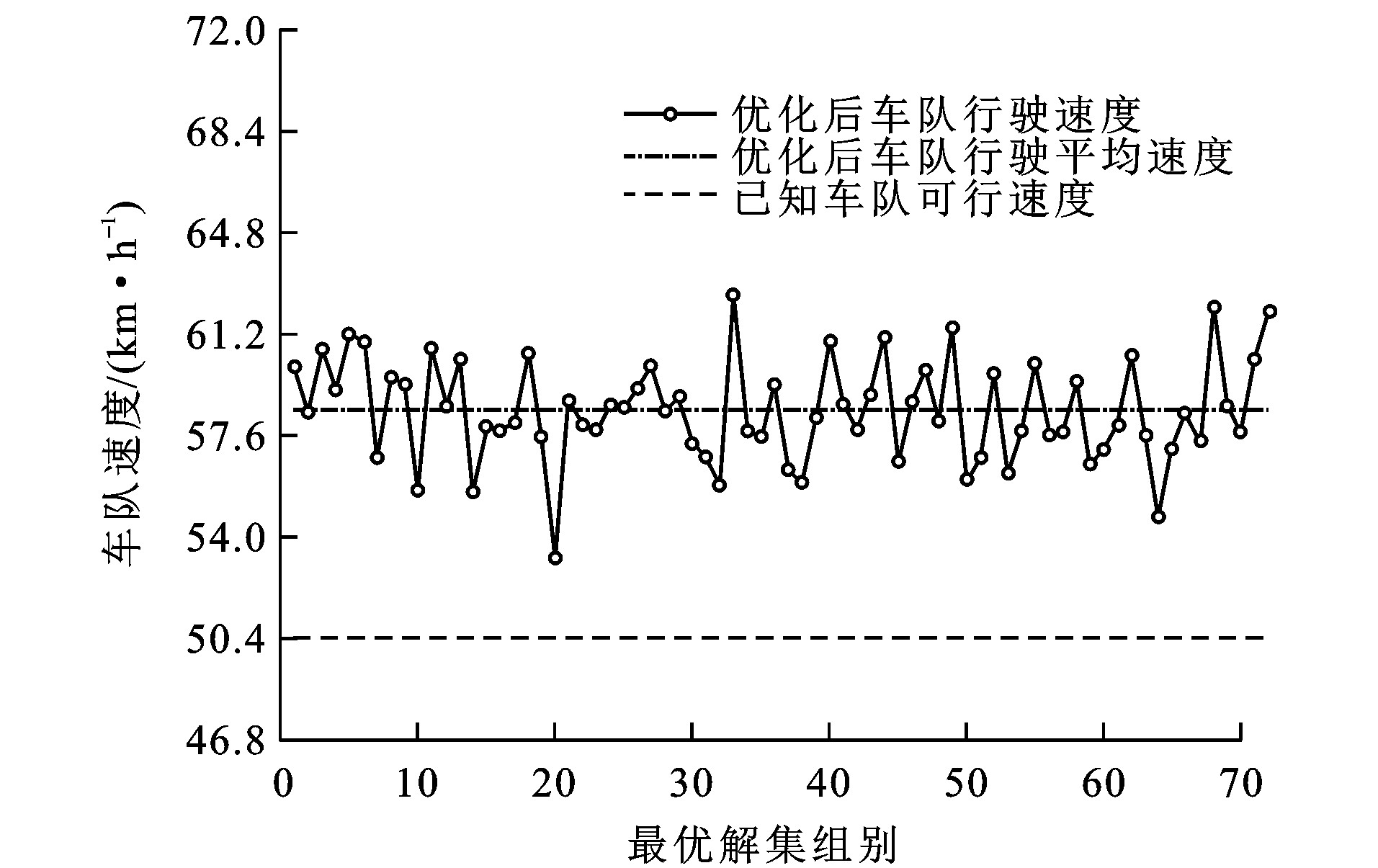
结合所设定的双向双车道路段车辆运行状态, 同时考虑车辆行驶里程、超越车辆数与单步超车过程的柔性化, 对分步式超车过程优化后可得表 3所示的最优控制策略。将获取的7 200个最优解分成72组, 计算每百组最优解中超车车辆的平均速度 $\bar{v}$ 为

$\bar{v} = \frac{\sum_{g = 1}^{72} \sum_{u = 100 g - 99}^{100 g} S_{1} / 100 t_{5}}{72} (35)$

式中: g为最优解的组号; u为各组中的变量序列。

如图 8所示: 经计算, 分步式超车过程中超车车辆平均速度 $\bar{v}$ 为14.02 m·s^-1, 相比初始跟驰状态车速提升16.8%, 超车车辆的最大平均速度 $\bar{v}_{\max}$ 为14.94 m·s^-1。

超车车辆在跟驰车队行驶时, 存在整体加速行驶阶段, 车队整体加速后的速度 $\bar{v}_{q} \leq \bar{v}_{\max}$ , 即车辆跟驰速度小于占用对向车道进行超车时的速度, 在此设定车队加速行驶速度为 $\bar{v}_{q} = \bar{v}_{\max} = 14.92 m \cdot s^{- 1}$ 。 $\bar{v}_{q}$ 为

表 3 分步式超车最优控制策略

Table 3. Optimal control strategy of step-by-step overtaking

车辆行驶距离/m	超越车队车辆数/veh	安全间隙后车减速度/ (m·s^-2)	安全间隙前车加速度/ (m·s^-2)	超车车辆入队减速度/ (m·s^-2)	超车车辆减速时间/s
169.69	4	4.27	2.11	4.28	2.19
169.58	3	4.77	3.07	3.52	1.70
169.48	3	4.51	2.98	4.58	1.54
169.19	4	4.32	2.54	4.63	1.16
169.18	3	4.41	2.64	3.71	2.21
︙	︙	︙	︙	︙	︙
168.22	3	4.42	2.69	4.47	2.08
167.59	3	4.79	3.01	4.07	1.65
167.58	3	4.87	2.76	4.39	1.23
167.19	3	4.65	3.58	3.92	2.15
167.11	4	5.23	2.92	4.25	2.13
︙	︙	︙	︙	︙	︙
166.88	3	4.63	3.05	3.96	1.70
166.76	3	5.09	3.00	3.82	1.52
166.69	3	5.03	3.78	3.39	1.27
166.63	4	5.47	3.04	3.84	2.00
166.42	3	4.22	2.45	4.73	0.94

下载: 导出CSV

| 显示表格

图 7 适应度曲线

Figure 7. Fitness degree curves

下载: 全尺寸图片幻灯片

图 8 分步式超车策略中超车车辆速度

Figure 8. Velocity of overtaking vehicle in step-by-step overtaking strategy

下载: 全尺寸图片幻灯片

图 9 分步式超车策略中车队速度

Figure 9. Velocity of platoon in step-by-step overtaking strategy

下载: 全尺寸图片幻灯片

$\begin{array}{l} \bar{v}_{q} = \sum_{g = 1}^{72} \frac{\sum_{u = 100 g - 99}^{100 g} v^{'}_{k} / 100}{72} (36) \\ v^{'}_{k} = \frac{(Ν - n) a_{3} t_{2} - n a_{4} t_{3}}{Ν} + v^{'}_{1} (37) \end{array}$

对分步式SVOP过程中车队车辆平均速度进行统计, 结果见图 9, 车队车辆平均速度 $\bar{v}_{q}$ 为16.27 m·s^-1, 相比自由加速行驶状态, 提升9.04%。

4. 结语

(1) 分析了车辆组队行驶状态下车队外车辆在存在对向行驶车辆的情况时面临的超车困难问题, 建立了SVOP模型, 说明了双向双车道中车辆超越车队时存在既不能完成超车又不能安全返回原车道的超车危险区域, 并且超车危险区域范围与车队车辆数及对向车辆行驶速度成正相关关系。

(2) 研究了车辆跟驰所需安全距离与前后车速度之间的关系, 为车辆入队所需安全间距提供了优化的速度匹配方案。

(3) 设计了分步式SVOP算法, 同时针对分步式SVOP过程中的三级车速引导问题提出了基于改进粒子群的分级约束多目标优化方法。

(4) 分别对车辆入队过程三级速度匹配的不同方案、改进PSO算法与传统PSO算法进行仿真结果对比, 结果表明: 改进的PSO算法相比传统PSO算法鲁棒性更强, 收敛速度更快, 所得最优控制策略使得SVOP过程中不仅安全性得到保障, 而且超车车辆和车队行驶效率同样得到提升, 进一步验证了算法的可行性。

(5) 分步式SVOP算法为超车车辆提供了驾驶行为引导信息, 但是由于驾驶人驾驶风格各异, 多目标优化后的最优控制策略不一定适应于每一位驾驶人, 根据驾驶人行为特征制定超车行为引导策略是下一步需要研究的重点。

图 1 超车危险区域曲面

Figure 1. Surface plot of dangerous overtaking area

下载: 全尺寸图片幻灯片

图 2 分步式超车

Figure 2. Step-by-step overtaking

下载: 全尺寸图片幻灯片

图 3 不同车速关系条件下安全间距分布

Figure 3. Safety distance distributions under different velocity relationships

下载: 全尺寸图片幻灯片

图 4 超车车速为36 km·h^-1时前、后车速与安全间距关系曲线

Figure 4. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 36 km·h^-1

下载: 全尺寸图片幻灯片

图 5 超车车速为72 km·h^-1时前、后车速与安全间距关系曲线

Figure 5. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 72 km·h^-1

下载: 全尺寸图片幻灯片

图 6 超车车速为90 km·h^-1时前、后车速与安全间距关系曲线

Figure 6. Relationship curves between speeds of front and rear vehicles and safety distance when overtaking velocity is 90 km·h^-1

下载: 全尺寸图片幻灯片

图 7 适应度曲线

Figure 7. Fitness degree curves

下载: 全尺寸图片幻灯片

图 8 分步式超车策略中超车车辆速度

Figure 8. Velocity of overtaking vehicle in step-by-step overtaking strategy

下载: 全尺寸图片幻灯片

图 9 分步式超车策略中车队速度

Figure 9. Velocity of platoon in step-by-step overtaking strategy

下载: 全尺寸图片幻灯片

表 1 v₅~v₇关系

Table 1. Relationship among v₅, v₆and v₇

方案	v₅与v₆关系	v₅与v₇关系	图示
1	v₅ > v₆	v₅ > v₇	3 (a)
2	v₅≤v₆	v₅ > v₇	3 (b)
3	v₅ > v₆	v₅≤ v₇	3 (c)
4	v₅≤v₆	v₅≤v₇	3 (d)

下载: 导出CSV

表 2 分步式超车仿真参数

Table 2. Simulation parameters of step-by-step overtaking

参数	数值
s₃/m	600
H/m	0.5
l₁、l₂/m	5
N/veh	30
a₂/ (m·s^-2)	4
a₃/ (m·s^-2)	4
a₄/ (m·s^-2)	7
v₀/ (m·s^-1)	12
v′k/ (m·s^-1)	10
v₁/ (m·s^-1)	10
t₃/s	1
t₄/s	0.2
t₁₁/s	3

下载: 导出CSV

表 3 分步式超车最优控制策略

Table 3. Optimal control strategy of step-by-step overtaking

车辆行驶距离/m	超越车队车辆数/veh	安全间隙后车减速度/ (m·s^-2)	安全间隙前车加速度/ (m·s^-2)	超车车辆入队减速度/ (m·s^-2)	超车车辆减速时间/s
169.69	4	4.27	2.11	4.28	2.19
169.58	3	4.77	3.07	3.52	1.70
169.48	3	4.51	2.98	4.58	1.54
169.19	4	4.32	2.54	4.63	1.16
169.18	3	4.41	2.64	3.71	2.21
︙	︙	︙	︙	︙	︙
168.22	3	4.42	2.69	4.47	2.08
167.59	3	4.79	3.01	4.07	1.65
167.58	3	4.87	2.76	4.39	1.23
167.19	3	4.65	3.58	3.92	2.15
167.11	4	5.23	2.92	4.25	2.13
︙	︙	︙	︙	︙	︙
166.88	3	4.63	3.05	3.96	1.70
166.76	3	5.09	3.00	3.82	1.52
166.69	3	5.03	3.78	3.39	1.27
166.63	4	5.47	3.04	3.84	2.00
166.42	3	4.22	2.45	4.73	0.94

下载: 导出CSV

参考文献(30)

[1]	ZHANG Wen-hui, DAI Jing, PEI Yu-long, et al. Drivers' visual search patterns during overtaking maneuvers on freeway[J]. International Journal of Environmental Research and Public Health, 2016, 13: 1-15.
[2]	RAWAT K, KATIYAR V K, GUPTA P. Two-lane traffic flow simulation model via cellular automaton[J]. International Journal of Vehicular Technology, 2012, 2012: 1-6.
[3]	王润琪, 周永军, 肖传恩. 双车道公路超车视距计算方法[J]. 交通运输工程学报, 2011, 11 (3): 68-73. doi: 10.3969/j.issn.1671-1637.2011.03.012 WANG Run-qi, ZHOU Yong-jun, XIAO Chuan-en. Calculation method of overtaking sight distance for dual-lane highway[J]. Journal of Traffic and Transportation Engineering, 2011, 11 (3): 68-73. (in Chinese). doi: 10.3969/j.issn.1671-1637.2011.03.012
[4]	许伦辉, 胡三根, 伍帅, 等. 考虑车辆运行特性的双车道超车模型[J]. 华南理工大学学报(自然科学版), 2015, 43 (4): 7-13, 27. doi: 10.3969/j.issn.1000-565X.2015.04.002 XU Lun-hui, HU San-gen, WU Shuai, et al. Overtaking model for two-lane highway considering vehicle running characteristics[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43 (4): 7-13, 27. (in Chinese). doi: 10.3969/j.issn.1000-565X.2015.04.002
[5]	CHENG Sen-lin, WANG Chuan-hai, ZHANG Shuang-teng, et al. Study on control strategy for personalised lane-change on highway[J]. The Journal of Engineering, 2018, 2018 (16): 1724-1730. doi: 10.1049/joe.2018.8269
[6]	LLORCA C, MORENO A T, GARCIA A. Modelling vehicles acceleration during overtaking manoeuvres[J]. IET Intelligent Transport Systems, 2016, 10 (3): 206-215. doi: 10.1049/iet-its.2015.0035
[7]	ATOMBO C, WU Chao-zhong, ZHONG Ming, et al. Investigating the motivational factors influencing drivers intentions to unsafe driving behaviours: speeding and overtaking violations[J]. Transportation Research Part F: Traffic Psychology and Behavior, 2016, 43: 104-121. doi: 10.1016/j.trf.2016.09.029
[8]	荣建, 刘世杰, 邵长桥, 等. 超车模型在双车道公路仿真系统中的应用研究[J]. 公路交通科技, 2007, 24 (11): 136-139. doi: 10.3969/j.issn.1002-0268.2007.11.030 RONG Jian, LIU Shi-jie, SHAO Chang-qiao, et al. Application of overtaking model in two-lane highway simulation system[J]. Journal of Highway and Transportation Research and Development, 2007, 24 (11): 136-139. (in Chinese). doi: 10.3969/j.issn.1002-0268.2007.11.030
[9]	党睿娜, 王建强, 李克强, 等. 高速公路行驶条件下的驾驶员换道特性[J]. 清华大学学报(自然科学报), 2013, 53 (10): 1481-1485. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201310022.htm DANG Rui-na, WANG Jian-qiang, LI Ke-qiang, et al, Driver lane change characteristics for various highway driving conditions[J]. Journal of Tsinghua University (Science and Technology), 2013, 53 (10): 1481-1485. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB201310022.htm
[10]	王畅, 付锐, 张琼, 等. 换道预警系统中参数TTC特性研究[J]. 中国公路学报, 2015, 28 (8): 91-100, 108. doi: 10.3969/j.issn.1001-7372.2015.08.012 WANG Chang, FU Rui, ZHANG Qiong, et al. Research on parameter TTC characteristics of lane change warning system[J]. China Journal of Highway and Transport, 2015, 28 (8): 91-100, 108. (in Chinese). doi: 10.3969/j.issn.1001-7372.2015.08.012
[11]	徐磊, 彭金栓. 基于Carsim和Simulink的超车换道仿真分析[J]. 科学技术与工程, 2014, 14 (29): 300-303. doi: 10.3969/j.issn.1671-1815.2014.29.058 XU Lei, PENG Jin-shuan. Simulation and analysis on overtaking lane change based on Simulink and Carsim[J]. Science Technology and Engineering, 2014, 14 (29): 300-303. (in Chinese). doi: 10.3969/j.issn.1671-1815.2014.29.058
[12]	柏伟, 李存军. 基于不同限速条件下的超车模型研究[J]. 交通运输系统工程与信息, 2013, 13 (2): 63-68, 95. doi: 10.3969/j.issn.1009-6744.2013.02.010 BAI Wei, LI Cun-jun. Overtaking model based on different limiting speed[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13 (2): 63-68, 95. (in Chinese). doi: 10.3969/j.issn.1009-6744.2013.02.010
[13]	熊晓夏, 陈龙, 梁军, 等. 危险换道驾驶行为预测方法研究[J]. 汽车工程, 2017, 39 (9): 1040-1046, 1067. https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201709010.htm XIONG Xiao-xia, CHEN Long, LIANG Jun, et al. A study on the driving behavior prediction of dangerous lane change[J]. Automotive Engineering, 2017, 39 (9): 1040-1046, 1067. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QCGC201709010.htm
[14]	李珣, 曲仕茹, 夏余. 车路协同环境下多车道车辆的协同换道规则[J]. 中国公路学报, 2014, 27 (8): 97-104. doi: 10.3969/j.issn.1001-7372.2014.08.013 LI Xun, QU Shi-ru, XIA Yu. Cooperative lane-changing rules on multilane under condition of cooperative vehicle and infrastructure system[J]. China Journal of Highway and Transport, 2014, 27 (8): 97-104. (in Chinese). doi: 10.3969/j.issn.1001-7372.2014.08.013
[15]	MILANÉS V, LLORCA D F, VILLAGRÁ J, et al. Intelligent automatic overtaking system using vision for vehicle detection[J]. Expert Systems with Applications, 2012, 39 (3): 3362-3373. doi: 10.1016/j.eswa.2011.09.024
[16]	CHEN Jun-jie, CAI Bai-gen, SHANGGUAN Wei, et al. Influence of Vehicle Cluster Driving Behavior on Traffic Flow Efficiency[C]//IEEE. 2017 Chinese Automation Congress. New York: IEEE, 2017: 6349-6354.
[17]	CHAPMAN J R, NOYCE D A. Influence of roadway geometric elements on driver behavior when overtaking bicycles on rural roads[J]. Journal of Traffic and Transportation Engineering (English Edition), 2014, 1 (1): 28-38. doi: 10.1016/S2095-7564(15)30086-6
[18]	ASAITHAMBI G, SHRAVANI F. Overtaking behavior of vehicles on undivided roads in non-lane based mixed traffic conditions[J]. Journal of Traffic and Transportation Engineering (English Edition), 2017, 4 (3): 252-261. doi: 10.1016/j.jtte.2017.05.004
[19]	杨晓光, 黄罗毅, 王吟松, 等. 基于车车通信的换道超车辅助系统设计与实现[J]. 公路交通科技, 2012, 29 (11): 120-124. doi: 10.3969/j.issn.1002-0268.2012.11.022 YANG Xiao-guang, HUANG Luo-yi, WANG Yin-song, et al. A novel lane change and overtaking assist system design and implementation based on vehicle-to-vehicle communication[J]. Journal of Highway and Transportation Research and Development, 2012, 29 (11): 120-124. (in Chinese). doi: 10.3969/j.issn.1002-0268.2012.11.022
[20]	KINNEAR N, HELMAN S, WALLBANK C, et al. An experimental study of factors associated with driver frustration and overtaking intentions[J]. Accident Analysis and Prevention, 2015, 79: 221-230. doi: 10.1016/j.aap.2015.03.032
[21]	VLAHOGIANNI E I, GOLIAS J C. Bayesian modeling of the microscopic traffic characteristics of overtaking in two-lane highways[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2012, 15 (3): 348-357. doi: 10.1016/j.trf.2012.02.002
[22]	HAJEK W, GAPONOVA I, FlEISCHER K H, et al. Workload-adaptive cruise control—a new generation of advanced driver assistance systems[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2013, 20: 108-120. doi: 10.1016/j.trf.2013.06.001
[23]	KOSUN C, OZDEMIR S. An entropy-based analysis of lane changing behavior: an interactive approach[J]. Traffic Injury Prevention, 2017, 18 (4): 441-447. doi: 10.1080/15389588.2016.1204446
[24]	YU Yue, EL KAMEL A, GONG Guang-hong, Modeling and simulation of overtaking behavior involving environment[J]. Advances in Engineering Software, 2014, 67: 10-21.
[25]	DIXIT S, FALLAH S, MONTANARO U, et al. Trajectory planning and tracking for autonomous overtaking: State-of-the-art and future prospects[J]. Annual Reviews in Control, 2018, 45: 76-86. doi: 10.1016/j.arcontrol.2018.02.001
[26]	XU Guo-qing, LIU Li, OU Yong-sheng, et al. Dynamic modeling of driver control strategy of lane-change behavior and trajectory planning for collision prediction[J]. IEEE Transportations on Intelligent Transportation Systems, 2012, 13 (3): 1138-1155.
[27]	YANG Da, ZHENG Shi-yu, WEN Cheng, et al. A dynamic lane-changing trajectory planning model for automated vehicles[J]. Transportation Research Part C: Emerging Technologies, 2018, 95: 228-247.
[28]	SUH J, CHAE H, YI K. Stochastic model-predictive control for lane change decision of automated driving vehicles[J]. IEEE Transactions on Vehicular Technology, 2018, 67 (6): 4771-4782.
[29]	ZHU Wen-xing, ZHANG Li-dong. A new car-following model for autonomous vehicles flow with mean expected velocity field[J]. Physica A: Statistical Mechanics and its Applications, 2018, 492: 2154-2165.
[30]	单晓峰, 夏东, 王昊. 双车道公路超车两难区域研究[J]. 公路交通科技, 2007, 24 (3): 111-114. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200703025.htm SHAN Xiao-feng, XIA Dong, WANG Hao. Dilemma zone in two-lane highways[J]. Journal of Highway and Transportation Research and Development, 2007, 24 (3): 111-114. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK200703025.htm

施引文献

期刊类型引用(6)

1.	戢晓峰，俸才梅，李武，韩春阳，覃文文. 双车道公路超车行为安全研究进展. 安全与环境学报. 2025(01): 21-40 . 百度学术
2.	钱立军，陈晨，陈健. 无信控交叉口环境下考虑驾驶员误差的集中式轨迹规划. 汽车工程. 2023(05): 768-776+785 . 百度学术
3.	Yang Liu，Congling Shi. Mandatory lane-changing decision making and planning in emergency situations. Transportation Safety and Environment. 2023(01): 44-52 . 必应学术
4.	秦严严，唐鸿辉，杨金滢，李淑庆. 混有网联车队的道路通行能力分析. 北京交通大学学报. 2022(01): 79-87 . 百度学术
5.	上官伟，李鑫，柴琳果，曹越，陈晶晶，庞豪杰，芮涛. 车路协同环境下混合交通群体智能仿真与测试研究综述. 交通运输工程学报. 2022(03): 19-40 . 本站查看
6.	李晓虎，麦乐，任杰，刘浩学，朱彤. 高速公路施工区自动车辆行驶轨迹优化方法. 交通信息与安全. 2020(03): 40-47 . 百度学术

其他类型引用(6)

资源附件(0)

访问统计

点击查看大图

图(9) / 表(3)

计量

文章访问数: 1257
HTML全文浏览量: 225
PDF下载量: 538
被引次数: 12

0. 引言
1. 双向双车道SVOP模型
1.1 SVOP模型建立
1.2 SVOP危险区域影响因素
2. 分步式SVOP算法
2.1 超车车辆速度与安全间隙匹配
2.2 车队安全间隙位置选取
3. 仿真结果分析
4. 结语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

双向双车道超车行为的智能车队间隙控制优化

doi: 10.19818/j.cnki.1671-1637.2019.02.016

作者简介:
陈俊杰(1989-), 男, 河北沧州人, 北京交通大学工学博士研究生, 从事车路协同自主车辆群体智能控制与优化技术研究

蔡伯根(1966-), 男, 江苏南通人, 北京交通大学教授, 工学博士

通讯作者:
上官伟(1979-), 男, 陕西乾县人, 北京交通大学教授, 工学博士

计量

Slot control optimization of intelligent platoon for dual-lane two-way overtaking behavior

Author Bio:
CHEN Jun-jie (1989-), male, doctoral student, junjiechen@bjtu.edu.cn

CAI Bai-gen (1966-), male, professor, PhD, bgcai@bjtu.edu.cn

SHANGGUAN Wei (1979-), male, professor, PhD, wshg@bjtu.edu.cn

0. 引言

1. 双向双车道SVOP模型

1.1 SVOP模型建立

1.2 SVOP危险区域影响因素

2. 分步式SVOP算法

2.1 超车车辆速度与安全间隙匹配

2.2 车队安全间隙位置选取

3. 仿真结果分析

4. 结语

期刊类型引用(6)

其他类型引用(6)

计量

目录

0. 引言

1. 双向双车道SVOP模型

1.1 SVOP模型建立

1.2 SVOP危险区域影响因素

2. 分步式SVOP算法

2.1 超车车辆速度与安全间隙匹配

2.2 车队安全间隙位置选取

3. 仿真结果分析

4. 结语

留言板

双向双车道超车行为的智能车队间隙控制优化

doi: 10.19818/j.cnki.1671-1637.2019.02.016

作者简介: 陈俊杰(1989-), 男, 河北沧州人, 北京交通大学工学博士研究生, 从事车路协同自主车辆群体智能控制与优化技术研究 蔡伯根(1966-), 男, 江苏南通人, 北京交通大学教授, 工学博士

通讯作者: 上官伟(1979-), 男, 陕西乾县人, 北京交通大学教授, 工学博士

计量

出版历程

Slot control optimization of intelligent platoon for dual-lane two-way overtaking behavior

Author Bio: CHEN Jun-jie (1989-), male, doctoral student, junjiechen@bjtu.edu.cn CAI Bai-gen (1966-), male, professor, PhD, bgcai@bjtu.edu.cn SHANGGUAN Wei (1979-), male, professor, PhD, wshg@bjtu.edu.cn

0. 引言

1. 双向双车道SVOP模型

1.1 SVOP模型建立

1.2 SVOP危险区域影响因素

2. 分步式SVOP算法

2.1 超车车辆速度与安全间隙匹配

2.2 车队安全间隙位置选取

3. 仿真结果分析

4. 结语

期刊类型引用(6)

其他类型引用(6)

计量

出版历程

目录

0. 引言

1. 双向双车道SVOP模型

1.1 SVOP模型建立

1.2 SVOP危险区域影响因素

2. 分步式SVOP算法

2.1 超车车辆速度与安全间隙匹配

2.2 车队安全间隙位置选取

3. 仿真结果分析

4. 结语

作者简介:
陈俊杰(1989-), 男, 河北沧州人, 北京交通大学工学博士研究生, 从事车路协同自主车辆群体智能控制与优化技术研究

蔡伯根(1966-), 男, 江苏南通人, 北京交通大学教授, 工学博士

通讯作者:
上官伟(1979-), 男, 陕西乾县人, 北京交通大学教授, 工学博士

Author Bio:
CHEN Jun-jie (1989-), male, doctoral student, junjiechen@bjtu.edu.cn

CAI Bai-gen (1966-), male, professor, PhD, bgcai@bjtu.edu.cn

SHANGGUAN Wei (1979-), male, professor, PhD, wshg@bjtu.edu.cn