基于变分模态分解和奇异值分解的结构模态参数识别方法

沈健; 赵文涛; 丁建明

doi:10.19818/j.cnki.1671-1637.2019.06.008

基于变分模态分解和奇异值分解的结构模态参数识别方法

doi: 10.19818/j.cnki.1671-1637.2019.06.008

1.
中铁二院工程集团有限责任公司科学技术研究院, 四川成都 610031
2.
西南交通大学牵引动力国家重点实验室, 四川成都 610031

基金项目:

国家自然科学基金项目 51875481

四川省重点研发项目 2017GZ0088

详细信息

作者简介:
沈健(1981-), 男, 四川西昌人, 中铁二院工程集团有限责任公司副研究员, 从事车线测试技术研究

中图分类号: U270.1
计量
- 文章访问数: 792
- HTML全文浏览量: 231
- PDF下载量: 436
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-30
- 刊出日期: 2019-12-25

Structural modal parameter identification method based on variational mode decomposition and singular value decomposition

1.
Research Institute of Science and Technology, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, Sichuan, China
2.
State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, Sichuan, China

More Information

Author Bio:
SHEN Jian (1981-), male, associate professor, 5435918@qq.com

Article Text (Baidu Translation)

摘要

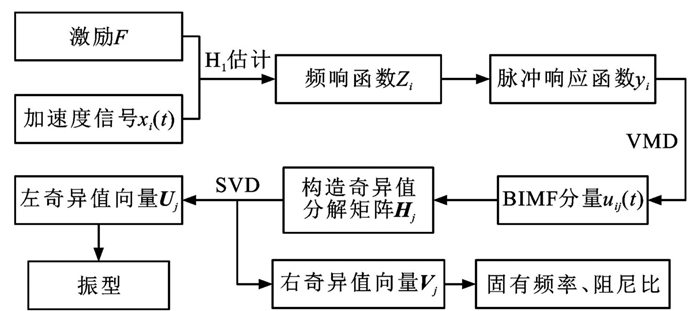
摘要: 为了准确获得结构的固有频率、阻尼比与振型, 将变分模态分解与奇异值分解相结合, 提出一种新的结构模态参数识别方法; 基于已有时频参数识别方法, 根据测量的脉冲激励与加速度响应估计系统的频响函数, 对系统的频响函数进行反傅里叶变换得到脉冲响应函数; 对各测点的脉冲响应函数进行变分模态分解, 得到与结构固有频率对应的本征模态分量; 提取本征模态分量的固有频率, 利用与固有频率相近的本征模态分量作为行向量构造奇异值分解矩阵, 对所构矩阵做奇异值分解, 利用最大奇异值重构左、右奇异值向量, 识别结构的振型、固有频率和阻尼比; 通过四自由度质量-弹簧-阻尼模态仿真试验和车体横梁锤击模态试验, 验证了所提出的模态参数识别方法的有效性。研究结果表明: 在四自由度理论模型参数识别中, 系统固有频率和阻尼比的识别结果与理论计算结果的最大相对误差分别不超过0.025%和1.490%, 理论计算与识别的1~4阶振型的模态置信度分别为0.999、1.000、0.999和0.999;在车体横梁锤击模态试验中, 提出方法识别的固有频率和阻尼比与理论计算结果的最大相对误差分别不超过1.57%和1.47%, 且车体横梁的理论振型与识别振型趋势相同。可见, 提出的方法能有效识别结构的模态参数。
- 车辆工程 /
- 结构 /
- 模态参数 /
- 脉冲响应函数 /
- 变分模态分解 /
- 奇异值分解 /
- 参数识别
Abstract: To obtain the structural natural frequency, damping ratio and vibration mode, a new modal parameter identification method was proposed by combining the variational mode decomposition with the singular value decomposition. Based on the existing time-frequency parameter identification method, the system frequency response function was estimated according to the measured impulse excitations and accelerations. The inverse Fourier transform was applied to the system frequency response function to obtain the impulse response function. The intrinsic mode components corresponding to the structural natural frequencies were obtained by executing the variational mode decomposition on the impulse response function for each measuring point. The natural frequencies of intrinsic mode components were extracted, and the intrinsic mode components close to the natural frequency were used as the row vectors to construct the singular value decomposition matrix, and the singular value decomposition was performed on the constructed matrix. The left and right singular value vectors reconstructed by the maximum singular values were used to identify the vibration mode, natural frequency and damping ratio of the structure. The effectiveness of the proposed modal parameter identification method was verified through a four-degree-of-freedom mass-spring-damping theoretical model and a hammering modal test on the vehicle body crossbeam. Research result indicates that in the parameter identification of four-degree-of-freedom theoretical model, the maximum relative errors of system natural frequencies and damping ratios between the identified and theoretical values are no more than 0.025% and 1.490%, respectively. The modal assurance criterions of 1 to 4-order vibration modes between the theoretical and identified values are 0.999, 1.000, 0.999 and 0.999, respectively. In the hammering modal test on the vehicle body crossbeam, the maximum relative errors of natural frequency and damping ratio between the results identified by the proposed method and the theoretical results are not more than 1.57% and 1.47%, respectively, and the theoretical and identified vibration modes have the same trend. Therefore, the proposed method can effectively identify the structural modal parameters.
- vehicle engineering /
- structure /
- modal parameter /
- impulse response function /
- variational mode decomposition /
- singular value decomposition /
- parameter identification

HTML全文

图 1 基于变分模态分解和奇异值分解的结构模态参数识别模型

Figure 1. Structure modal parameter identification model based on variational mode decomposition and singular value decomposition

下载: 全尺寸图片幻灯片

图 2 四自由度质量-弹簧-阻尼系统

Figure 2. Four-degree-of-freedom mass-spring-damping system

下载: 全尺寸图片幻灯片

图 3 m₁的加速度响应曲线

Figure 3. Acceleration response curves of m₁

下载: 全尺寸图片幻灯片

图 4 m₁的加速度响应频谱

Figure 4. Acceleration response frequency spectrums of m₁

下载: 全尺寸图片幻灯片

图 5 x₁₄经变分模态分解得到的分解信号

Figure 5. Decomposed signals of x₁₄ obtained by VMD

下载: 全尺寸图片幻灯片

图 6 经变分模态分解得到的分解信号频谱

Figure 6. Frequency spectrums of decomposed signals obtained by VMD

下载: 全尺寸图片幻灯片

图 7 x₁₄由经验模态分解得到的分解信号

Figure 7. Decomposed signals of x₁₄ obtained by EMD

下载: 全尺寸图片幻灯片

图 8 由经验模态分解得到的分解信号频谱

Figure 8. Frequency spectrums of decomposed signals obtained by EMD

下载: 全尺寸图片幻灯片

图 9 参数识别过程

Figure 9. Process of parameter identification

下载: 全尺寸图片幻灯片

图 10 理论振型与识别振型比较

Figure 10. Comparison of identified and theoretical vibration modes

下载: 全尺寸图片幻灯片

图 11 MAC矩阵

Figure 11. MAC matrix

下载: 全尺寸图片幻灯片

图 12 动车组车体横梁结构及测点布置

Figure 12. Structure and measuring points arrangement of vehicle body crossbeam of EMU

下载: 全尺寸图片幻灯片

图 13 车体横梁锤击模态试验

Figure 13. Hammering modal test on vehicle body crossbeam

下载: 全尺寸图片幻灯片

图 14 锤击模态试验数据和H₁估计

Figure 14. Hammering modal test data and H₁ estimation

下载: 全尺寸图片幻灯片

图 15 本文方法识别1阶模态参数

Figure 15. First-order modal parameters obtained by method in this paper

下载: 全尺寸图片幻灯片

图 16 本文方法识别2阶模态参数

Figure 16. Second-order modal parameter obtained by method in this paper

下载: 全尺寸图片幻灯片

图 17 本文方法识别3阶模态参数

Figure 17. Third-order modal parameter obtained by method in this paper

下载: 全尺寸图片幻灯片

图 18 本文方法识别部分测点的模态振型

Figure 18. Modal vibration modes of some measuring points identified by method in this paper

下载: 全尺寸图片幻灯片

图 19 车体横梁前4阶模态振型

Figure 19. First four orders vibration modes of vehicle body crossbeam

下载: 全尺寸图片幻灯片

表 1 仿真信号模态参数识别结果

Table 1. Modal parameter identification results of simulation signals

模态阶数		1	2	3	4
固有频率/Hz	本文方法	61.163	227.955	460.121	848.794
	传统方法	60.987~61.203	227.873~227.964	460.032~460.155	≤848.724
	HHT方法	60.559~67.399	214.119~234.096	423.554~460.169
	理论值	61.148	227.951	460.183	848.771
固有频率的相对误差/%	本文方法	0.025	0.002	0.013	0.003
	传统方法	0.089~0.263	0.006~0.034	0.006~0.033	≤0.006
	HHT方法	0.963~10.223	2.696~6.068	0.003~7.959
阻尼比/%	本文方法	0.126	0.529	0.244	0.045
	传统方法	0.136~0.280	0.530	0.240~0.250	≤0.049
	HHT方法	≤0.189	0.499~0.522	0.212~0.268
	理论值	0.126	0.537	0.245	0.045
阻尼比的相对误差/%	本文方法	0	1.490	0.408	0
	传统方法	7.937~122.222	1.304	2.041	8.889
	HHT方法	≤50	2.793~7.076	9.388~13.469

下载: 导出CSV

表 2 模态参数识别结果对比

Table 2. Comparison of modal parameter identification results

模态阶数		1	2	3	4
固有频率/Hz	本文方法	66.113	212.886	444.962	754.787
	传统方法	63.783~69.194	210.443~220.124	438.926~458.232	754.789~764.964
	仿真结果	65.072	214.086	447.108	762.899
固有频率的相对误差/%	本文方法	1.57	0.56	0.48	1.08
固有频率的相对误差/%	传统方法	1.981~6.335	1.702~2.820	1.830~2.488	0.271~1.063
阻尼比/%	本文方法	1.47	0.55	0.25	0.14
阻尼比/%	传统方法	1.41~2.51	0.53~0.72	0.23~0.31	0.14~0.17

下载: 导出CSV

参考文献(30)

[1]	卢兆刚, 郝志勇, 杨陈, 等. 基于模态分析及优化设计技术的低噪声齿轮室罩的设计[J]. 振动与冲击, 2010, 29(10): 239-243. doi: 10.3969/j.issn.1000-3835.2010.10.051 LU Zhao-gang, HAO Zhi-yong, YANG Chen, et al. Design on low noise gear-cover based on modal analysis and optimization design technology[J]. Journal of Vibration and Shock, 2010, 29(10): 239-243. (in Chinese). doi: 10.3969/j.issn.1000-3835.2010.10.051
[2]	ZANG C, SCHWINGSHACKL C, EWIBS D J. Model validation for structural dynamic analysis: an approach to the Sandia structural dynamics challenge[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(29-32): 2645-2659. doi: 10.1016/j.cma.2007.07.034
[3]	韩伟, 贾启芬, 邱家俊. 异步电机定子的振动与模态分析[J]. 振动与冲击, 2012, 31(17): 91-94. doi: 10.3969/j.issn.1000-3835.2012.17.015 HAN Wei, JIA Qi-fen, QIU Jia-jun. Vibration and modal analysis for stator of an induction motor[J]. Journal of Vibration and Shock, 2012, 31(17): 91-94. (in Chinese). doi: 10.3969/j.issn.1000-3835.2012.17.015
[4]	KOUREHLI S S, BAGHERI A, AMIRI G G, et al. Structural damage detection using incomplete modal data and incomplete static response[J]. KSCE Journal of Civil Engineering, 2013, 17(1): 216-223. doi: 10.1007/s12205-012-1864-2
[5]	AU F T K, CHENG Y S, THAM L G, et al. Structural damage detection based on a micro-genetic algorithm using incomplete and noisy modal test data[J]. Journal of Sound and Vibration, 2003, 259(5): 1081-1094. doi: 10.1006/jsvi.2002.5116
[6]	BAYRAKTAR A, ALTUNISIK A C, TÜRKER T. Structural condition assessment of Birecik Highway Bridge using operational modal analysis[J]. International Journal of Civil Engineering, 2016, 14(1): 35-46. doi: 10.1007/s40999-016-0010-9
[7]	DOEBLING S W, FARRAR C R, PRIME M B, et al. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: a literature review[R]. Los Alamos: Los Alamos National Laboratory, 1996.
[8]	董冠华, 殷勤, 刘蕴, 等. 基于模态分析理论的结合部动刚度辨识[J]. 振动与冲击, 2017, 36(20): 125-131. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201720020.htm DONG Guan-hua, YIN Qin, LIU Yun, et al. A study on the identification of joints dynamic stiffness based on modal analysis[J]. Journal of Vibration and Shock, 2017, 36(20): 125-131. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201720020.htm
[9]	REYNDERS E. System identification methods for (operational) modal analysis: review and comparison[J]. Archives of Computational Methods in Engineering, 2012, 19(1): 51-124. doi: 10.1007/s11831-012-9069-x
[10]	段虎明, 秦树人, 李宁. 频率响应函数估计方法综述[J]. 振动与冲击, 2008, 27(5): 48-52. doi: 10.3969/j.issn.1000-3835.2008.05.013 DUAN Hu-ming, QIN Shu-ren, LI Ning. Measurement methods review for frequency response function[J]. Journal of Vibration and Shock, 2008, 27(5): 48-52. (in Chinese). doi: 10.3969/j.issn.1000-3835.2008.05.013
[11]	罗钧, 刘纲, 黄宗明. 基于随机减量法的非平稳激励下模态参数识别[J]. 振动与冲击, 2015, 34(21): 19-24, 64. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201521005.htm LUO Jun, LIU Gang, HUANG Zong-ming. Modal parametric identification under non-stationary excitation based on random decrement method[J]. Journal of Vibration and Shock, 2015, 34(21): 19-24, 64. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201521005.htm
[12]	杨佑发, 李帅, 李海龙. 环境激励下结构模态参数识别的改进ITD法[J]. 振动与冲击, 2014, 33(1): 194-199. doi: 10.3969/j.issn.1000-3835.2014.01.033 YANG You-fa, LI Shuai, LI Hai-long. Improved ITD method for structural modal parameter identification under ambient excitation[J]. Journal of Vibration and Shock, 2014, 33(1): 194-199. (in Chinese). doi: 10.3969/j.issn.1000-3835.2014.01.033
[13]	蒲黔辉, 洪彧, 王高新, 等. 快速特征系统实现算法用于环境激励下的结构模态参数识别[J]. 振动与冲击, 2018, 37(6): 55-60. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201806009.htm PU Qian-hui, HONG Yu, WANG Gao-xin, et al. Fast eigensystem realization algorithm based structural modal parameters identification for ambient tests[J]. Journal of Vibration and Shock, 2018, 37(6): 55-60. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201806009.htm
[14]	马维金, 熊诗波. 基于LSCE算法和FDD算法的振动筛动态特性研究[J]. 振动、测试与诊断, 2003, 23(3): 195-198. doi: 10.3969/j.issn.1004-6801.2003.03.011 MA Wei-jin, XIONG Shi-bo. Modal parameters identification of vibrant screen based on LSCE and FDD techniques[J]. Journal of Vibration, Measurement and Diagnosis, 2003, 23(3): 195-198. (in Chinese). doi: 10.3969/j.issn.1004-6801.2003.03.011
[15]	杨和振, 李华军, 黄维平. 海洋平台结构环境激励的实验模态分析[J]. 振动与冲击, 2005, 24(2): 129-133. doi: 10.3969/j.issn.1000-3835.2005.02.033 YANG He-zhen, LI Hua-jun, HUANG Wei-ping. Experimental modal analysis of offshore platform under operational conditions[J]. Journal of Vibration and Shock, 2005, 24(2): 129-133. (in Chinese). doi: 10.3969/j.issn.1000-3835.2005.02.033
[16]	应怀樵, 刘进明, 沈松. 半功率带宽法与INV阻尼计法求阻尼比的研究[J]. 噪声与振动控制, 2006(2): 4-6. doi: 10.3969/j.issn.1006-1355.2006.02.002 YING Huai-qiao, LIU Jin-ming, SHEN Song. Half-power bandwidth method and INV damping ration solver study[J]. Noise and Vibration Control, 2006(2): 4-6. (in Chinese). doi: 10.3969/j.issn.1006-1355.2006.02.002
[17]	BRINCKER R, ZHANG Ling-mi, ANDERSEN P. Modal identification of output-only systems using frequency domain decomposition[J]. Smart Materials and Structures, 2001, 10(3): 441-445. doi: 10.1088/0964-1726/10/3/303
[18]	裴强, 王丽. 结构参数识别方法研究[J]. 大连大学学报, 2013, 34(3): 36-44. doi: 10.3969/j.issn.1008-2395.2013.03.009 PEI Qiang, WANG Li. Review of parameter identification methods for vibrating system[J]. Journal of Dalian University, 2013, 34(3): 36-44. (in Chinese). doi: 10.3969/j.issn.1008-2395.2013.03.009
[19]	NIELD S A, WILLIAMS M S, MCFADDEN P D. Nonlinear vibration characteristics of damaged concrete beams[J]. Journal of Structural Engineering, 2003, 129(2): 260-280. doi: 10.1061/(ASCE)0733-9445(2003)129:2(260)
[20]	续秀忠, 张志谊, 华宏星, 等. 应用时频分析方法辨识时变系统的模态参数[J]. 振动工程学报, 2003, 16(3): 358-362. doi: 10.3969/j.issn.1004-4523.2003.03.020 XU Xiu-zhong, ZHANG Zhi-yi, HUA Hong-xing, et al. Identification of time-varying modal parameters by a linear time-frequency method[J]. Journal of Vibration Engineering, 2003, 16(3): 358-362. (in Chinese). doi: 10.3969/j.issn.1004-4523.2003.03.020
[21]	DING Jian-ming, DING Cheng-cheng. Automatic detection of a wheelset bearing fault using a multi-level empirical wavelet transform[J]. Measurement, 2019, 134: 179-192.
[22]	罗光坤, 张令弥. 基于Morlet小波变换的模态参数识别研究[J]. 振动与冲击, 2007, 26(7): 135-138. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200707033.htm LUO Guang-kun, ZHANG Ling-mi. Study on identification of modal parameters based on Morlet wavelet transformation[J]. Journal of Vibration and Shock, 2007, 26(7): 135-138. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ200707033.htm
[23]	HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A—Mathematical Physical and Engineering Sciences, 1998, 454(1): 903-995.
[24]	边涛, 谢寿生, 刘云龙. 基于HHT的拉杆转子结构模态参数识别[J]. 噪声与振动控制, 2017, 37(5): 23-28. https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK201705007.htm BIAN Tao, XIE Shou-sheng, LIU Yun-long. Modal parameters identification of rod fastening rotors based on HHT[J]. Noise and Vibration Control, 2017, 37(5): 23-28. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZSZK201705007.htm
[25]	闵志华, 孙利民, 孙智, 等. 基于小波变换和奇异值分解的模态参数识别方法[J]. 同济大学学报(自然科学版), 2009, 37(4): 460-465. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200904010.htm MIN Zhi-hua, SUN Li-min, SUN Zhi, et al. Modal parameters identification method based on wavelet transform and singular value decomposition[J]. Journal of Tongji University (Natural Science), 2009, 37(4): 460-465. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200904010.htm
[26]	DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[27]	丁建明, 王晗, 林建辉, 等. 基于EMD-Hankel-SVD的高速列车万向轴动不平衡检测[J]. 振动与冲击, 2015, 34(9): 164-170. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201509032.htm DING Jian-ming, WANG Han, LIN Jian-hui, et al. Detection of dynamic imbalance due to cardan shaft in high-speed train based on EMD-Hankel-SVD method[J]. Journal of Vibration and Shock, 2015, 34(9): 164-170. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201509032.htm
[28]	NI Ping-he, LI Jun, HAO Hong, et al. Time-varying system identification using variational mode decomposition[J]. Structural Control and Health Monitoring, 2018, 25(6): e2175-1-20.
[29]	BAGHERI A, OZBULUT O E, HARRIS D K. Structural system identification based on variational mode decomposition[J]. Journal of Sound and Vibration, 2018, 417: 182-197.
[30]	荣双龙, 李传日, 徐飞, 等. 试验模态分析最佳测试点选取方法的优化[J]. 北京航空航天大学学报, 2014, 40(4): 536-543. https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK201404019.htm RONG Shuang-long, LI Chuan-ri, XU Fei, et al. Method optimization of optimum measurement point selection in experiential modal analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(4): 536-543. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BJHK201404019.htm