Improved algorithm of cable force for one-time cable tensioning on steel tube arch ribs with segmental hoisting
-
摘要: 为改善大跨钢管拱肋分段吊装扣索索力常用算法迭代效率低、计算时耗长, 且忽略了温变影响等不足, 建立了可考虑温变影响和提高计算效率的改进算法; 基于材料力学和几何学相关知识, 推导了吊装过程中拱肋位移变化与温变的理论关系, 并在计入温变引起索长和拱肋位移改变的情况下, 推导出扣索索力变化与温变的理论关系; 基于扣索一次张拉法和ANSYS零阶优化法, 开发了考虑温变影响且在迭代子步中对程序自动搜索实施宏观调控的扣索索力计算程序; 运用改进算法对某主跨300 m钢管混凝土拱桥开展了分段吊装施工控制分析。分析结果表明: 推导的理论公式和有限元分析结果的变化规律一致, 拱肋位移变化的最大相对误差为11%, 索力变化的最大相对误差为18%, 均能满足工程精度要求; 与原算法相比, 采用改进算法的迭代次数由26次缩减到17次, 迭代效率提高了35%, 计算索力与实测索力的最大偏差由276 kN减小到100 kN; 拱肋松索成拱位移理论值与实测值的最大偏差为7 mm, 成拱线形正常; 建立的改进算法可实现扣索一次张拉, 提高迭代效率和计算精度, 运用改进算法控制大跨钢管拱肋吊装施工可使拱肋松索成拱线形满足设计要求。Abstract: To improve the defects of low iteration efficiency, long calculation time and neglecting the influence of temperature change of common calculation methods for cable force of long-span steel tube arch ribs during the segmental hoisting, an improved algorithm considering the influence of temperature change and improving the calculation efficiency was established. Based on the knowledge of material mechanics and geometry, the theoretical relationship between the changes of arch rib displacement and temperature during the hoisting was deduced, and the theoretical relationship between the changes of cable force and temperature was deduced considering the changes of cable length and arch rib displacement caused by the temperature change. Based on the one-time cable tensioning method and the zero order optimization method in ANSYS, a calculation program of cable force was developed considering the influence of temperature change and implementing the macro-control on the automatic search in the iteration sub step. The construction control analysis of segmental hoisting for a concrete filled steel tube arch bridge with a main span of 300 m was carried out with the improved algorithm. Analysis result shows that the results of derived theoretical formula are consistent with the change rules of finite element analysis results. The maximum relative error of displacement change of arch rib is 11%, and the maximum relative error of cable force change is 18%, both can meet the engineering accuracy requirements. Comparing with the original algorithm, the iteration number reduces from 26 to 17, the iteration efficiency increases by 35%, and the maximum deviation of cable force between the calculated and measured values reduces from 276 kN to 100 kN. The maximum deviation of arch rib displacement between the theoretical and the measured values is 7 mm after loosening cables and arched, and the arched alignment is normal. The established improved algorithm can realize the one-time cable tensioning and improve the iteration efficiency and calculation accuracy. The arch rib alignment after loosening cables and arched can meet the design requirements when using the improved algorithm to control the hoisting construction of long span steel tube arch rib.
-
表 1 拱肋各节段扣索体系几何参数
Table 1. Geometric parameters of cable system for each segment of arch rib
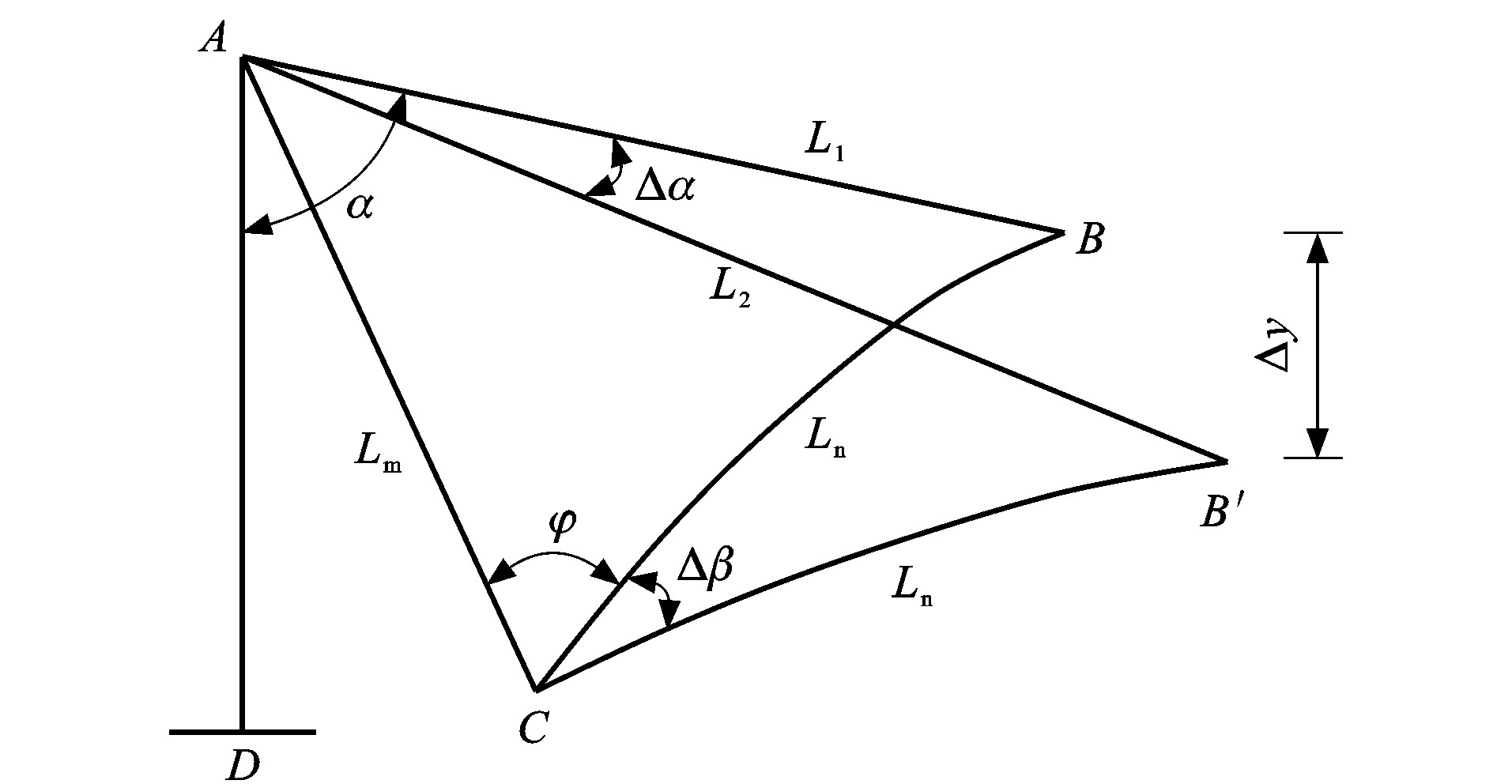
索号 1# 2# 3# 4# 5# 6# 7# 8# 9# 10# 11# 12# Lm/m 49.09 49.85 50.61 51.37 52.13 52.89 53.65 54.41 55.18 56.85 57.14 57.52 L1/m 44.88 51.07 57.90 67.03 75.96 85.31 94.92 104.69 119.47 134.67 149.58 159.54 Ln/m 17.23 40.69 52.01 64.46 75.31 85.98 96.49 106.60 122.22 137.39 152.45 164.25 α/(°) 35.94 60.86 69.40 76.34 80.58 83.59 85.72 87.20 88.74 89.14 89.60 89.62 φ/(°) 65.87 67.84 68.72 69.70 70.55 71.36 72.16 73.18 74.07 75.31 76.32 75.22 A/cm2 6.95 9.73 9.73 8.34 8.34 9.73 9.73 8.34 11.12 18.07 20.85 27.80 表 2 节段吊装预抬量
Table 2. Pre-cambers of segmental hoisting
mm 扣索编号 2# 3# 4# 5# 6# 7# 8# 9# 10# 11# 12# 13# 贵阳岸上游 2.56 -0.68 -0.25 -3.76 -2.13 -7.47 -2.75 -14.26 -0.07 -6.07 13.65 2.89 贵阳岸下游 2.59 -0.82 0.05 -4.16 -1.17 -8.20 -2.56 -14.93 -11.44 -7.12 17.52 2.91 遵义岸下游 1.94 -0.50 0.82 -2.77 -1.14 -5.09 -0.89 -8.84 1.87 -11.60 13.58 12.74 遵义岸上游 1.92 -0.62 0.71 -2.87 -0.60 -5.34 -1.02 -9.34 -5.17 -9.01 11.86 19.86 -
[1] GRANATA M F, MARGIOTTA P, RECUPERO A, et al. Partial elastic scheme method in cantilever construction of concrete arch bridges[J]. Journal of Bridge Engineering, 2013, 18: 663-672. doi: 10.1061/(ASCE)BE.1943-5592.0000396 [2] BOOTHBY T E, DOMALIK D E, DALAL V A. Service load response of masonry arch bridges[J]. Journal of Structural Engineering, 1998, 124: 17-23. doi: 10.1061/(ASCE)0733-9445(1998)124:1(17) [3] FANNING P J, BOOTHBY T E. Three-dimensional modeling and full-scale testing of stone arch bridges[J]. Computers and Structures, 2001, 79(29/30): 2645-2662. [4] MOHAMMADZADEH S, MIRI A, NOURI M. Enhancing the structural performance of masonry arch bridges with ballast mats[J]. Journal of Performance of Constructed Facilities, 2017, 31(5): 04017089-1-10. doi: 10.1061/(ASCE)CF.1943-5509.0001080 [5] 姚国文, 晁阳, 吴海军, 等. 中承式钢管混凝土劲性骨架拱桥拱肋吊装施工控制[J]. 桥梁建设, 2017, 47(5): 107-111. doi: 10.3969/j.issn.1003-4722.2017.05.019YAO Guo-wen, CHAO Yang, WU Hai-jun, et al. Construction control of hoisting and installation of arch rib of a half-through CFST stiff skeleton arch bridge[J]. Bridge Construction, 2017, 47(5): 107-111. (in Chinese). doi: 10.3969/j.issn.1003-4722.2017.05.019 [6] 郑皆连, 王建军, 冯智, 等. 钢管混凝土拱段真空辅助灌注工艺试验[J]. 中国公路学报, 2014, 27(6): 44-50. doi: 10.3969/j.issn.1001-7372.2014.06.006ZHENG Jie-lian, WANG Jian-jun, FENG Zhi, et al. Vacuum aided concrete grouting process test of concrete filled steel tube arch segment[J]. China Journal of Highway and Trasport, 2014, 27(6): 44-50. (in Chinese). doi: 10.3969/j.issn.1001-7372.2014.06.006 [7] 郭金亮, 栗超, 曹忠良. 大跨度上承式钢管混凝土拱桥拱肋吊装施工控制[J]. 公路, 2017(9): 179-185. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL201709041.htmGUO Jin-liang, LI Chao, CAO Zhong-liang. Construction control of arch rib lifting of long span concrete filled steel tube arch bridge[J]. Highway, 2017(9): 179-185. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL201709041.htm [8] 薛俊青, 陈宝春, 林健辉. 空心板延伸桥面板桥温度胀缩变形研究[J]. 桥梁建设, 2018, 48(2): 37-42. doi: 10.3969/j.issn.1003-4722.2018.02.007XUE Jun-qing, CHEN Bao-chun, LIN Jian-hui. Study of temperature expansion and contraction deformation of bridges with their deck slabs extended by hollow slabs[J]. Bridge Construction, 2018, 48(2): 37-42. (in Chinese). doi: 10.3969/j.issn.1003-4722.2018.02.007 [9] 王友彪. 大跨度钢管混凝土拱桥温度场及温度效应分析[D]. 成都: 西南交通大学, 2013.WANG You-biao. Analysis of temperature field and temperature effects on long-span CFST arch bridge[D]. Chengdu: Southwest Jiaotong University, 2013. (in Chinese). [10] 徐岳, 展丙来, 李扬, 等. 钢管混凝土拱桥斜拉扣挂施工扣索索力的优化计算方法[J]. 公路交通科技, 2016, 33(6): 61-67. doi: 10.3969/j.issn.1002-0268.2016.06.010XU Yue, ZHAN Bing-lai, LI Yang, et al. An optimum calculation method of cable force of CFST arch bridge in inclined cable hoisting construction[J]. Journal of Highway and Transportation Research and Development, 2016, 33(6): 61-67. (in Chinese). doi: 10.3969/j.issn.1002-0268.2016.06.010 [11] GAO Xin, LIU Li-jing, YAO Shu-kui, et al. Commonly encountered damages in cable members of CFST arch bridge and detection methods[J]. Key Engineering Materials, 2014, 619: 71-80. doi: 10.4028/www.scientific.net/KEM.619.71 [12] GU Ying, LI Yao-dong, LIU Sai-zhi. Research on construction control of long-span CFST arch bridge[J]. Applied Mechanics and Materials, 2015, 777: 88-93. doi: 10.4028/www.scientific.net/AMM.777.88 [13] 郝聂冰, 顾安邦. 500 m级钢管混凝土拱桥施工控制[J]. 西南交通大学学报, 2015, 50(4): 635-640. doi: 10.3969/j.issn.0258-2724.2015.04.010HAO Nie-bing, GU An-bang. Construction control of 500 m scale concrete-filled steel tubular arch bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(4): 635-640. (in Chinese). doi: 10.3969/j.issn.0258-2724.2015.04.010 [14] 胡大琳, 陈定市, 赵小由, 等. 大跨径钢筋混凝土拱桥悬臂浇筑施工控制[J]. 交通运输工程学报, 2016, 16(1): 25-36. doi: 10.3969/j.issn.1671-1637.2016.01.004HU Da-lin, CHEN Ding-shi, ZHAO Xiao-you, et al. Construction control of cantilever casting of long span reinforced concrete arch bridge[J]. Journal of Traffic and Transportation Engineering, 2016, 16(1): 25-36. (in Chinese). doi: 10.3969/j.issn.1671-1637.2016.01.004 [15] 张治成, 叶贵如, 王云峰. 大跨度拱桥拱肋线形调整中的扣索索力优化[J]. 工程力学, 2004, 21(6): 187-192. doi: 10.3969/j.issn.1000-4750.2004.06.031ZHANG Zhi-cheng, YE Gui-ru, WANG Yun-feng. Optimization of stayed-buckle cable forces during adjustment of the line-shape on long span arch bridge[J]. Engineering Mechanics, 2004, 21(6): 187-192. (in Chinese). doi: 10.3969/j.issn.1000-4750.2004.06.031 [16] 刘邵平, 张敏, 段永胜. 基于零阶优化法的大宁河大桥扣索索力计算[J]. 市政技术, 2009, 27(4): 354-356, 364. doi: 10.3969/j.issn.1009-7767.2009.04.009LIU Shao-ping, ZHANG Min, DUAN Yong-sheng. Cable force calculation of Daninghe Bridge based on zero-order optimization method[J]. Municipal Engineering Technology, 2009, 27(4): 354-356, 364. (in Chinese). doi: 10.3969/j.issn.1009-7767.2009.04.009 [17] 徐岳, 申成岳, 朱谊彪, 等. 确定拱桥斜拉扣挂施工扣索张力的改进迭代算法[J]. 桥梁建设, 2016, 46(2): 65-69. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201602012.htmXU Yue, SHEN Cheng-yue, ZHU Yi-biao, et al. Improved iteration algorithm for determination of tension of fastening stays for cantilever construction of arch bridge[J]. Bridge Construction, 2016, 46(2): 65-69. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201602012.htm [18] 李哲, 赵东升, 颜东煌, 等. 大跨度钢管混凝土拱桥制造线形计算方法研究[J]. 中外公路, 2015, 35(4): 107-110. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201504029.htmLI Zhe, ZHAO Dong-sheng, YAN Dong-huang, et al. Study on manufacturing line shape calculation method for large span concrete filled steel tube arch bridge[J]. Journal of China and Foreign Highway, 2015, 35(4): 107-110. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201504029.htm [19] 周建庭, 刘建, 周文, 等. 温度变化对钢管混凝土拱桥斜拉扣挂预抬值与主拱圈线形的影响分析[J]. 中外公路, 2017, 37(4): 62-66. https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201704016.htmZHOU Jian-ting, LIU Jian, ZHOU Wen, et al. Analysis of temperature change on pre-lifting value of cable-stayed buckling and alignment of main arch ring of concrete filled steel tubular arch bridge[J]. Journal of China and Foreign Highway, 2017, 37(4): 62-66. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GWGL201704016.htm [20] DUDAREV A, BREMER J, MULDER T, et al. New bridge temperature sensor for superconducting magnets and other cryogenic applications[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 9000904. [21] WANG Yuan-feng, MA Yi-shuo, HAN Bing, et al. Temperature effect on creep behavior of CFST arch bridge[J]. Journal of Bridge Engineering, 2013, 18: 1397-1405. doi: 10.1061/(ASCE)BE.1943-5592.0000484 [22] FARRERAS-ALCOVER I, CHRYSSANTHOPOULOS M K, ANDERSEN J E. Data-based models for fatigue reliability of orthotropic steel bridge decks based on temperature, traffic and strain monitoring[J]. International Journal of Fatigue, 2017, 95: 104-119. doi: 10.1016/j.ijfatigue.2016.09.019 [23] KIM S H, PARK S J, WU J X, et al. Temperature variation in steel box girders of cable-stayed bridges during construction[J]. Journal of Constructional Steel Research, 2015, 112: 80-92. doi: 10.1016/j.jcsr.2015.04.016 [24] LEI Xiao, JIANG Han-wan, WANG Jie, et al. Temperature effects on horizontally curved concrete box-girder bridges with single-column piers[J]. Journal of Aerospace Engineering, 2019, 32(3): 04019008-1-14. doi: 10.1061/(ASCE)AS.1943-5525.0000992 [25] AU F T K, THAM L G, TONG M, et al. Temperature monitoring of steel bridges[J]. Health Monitoring and Management of Civil Infrastructure Systems, 2001, 4337: 282-291. doi: 10.1117/12.435603 [26] 郑志明, 周建庭, 梁雄, 等. 大跨钢管混凝土拱桥实测与理论温差变形分析[J]. 重庆交通大学学报(自然科学版), 2008, 27(增): 843-848. https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT2008S1000.htmZHENG Zhi-ming, ZHOU Jian-ting, LIANG Xiong, et al. Analysis on measured deformation and theoretic deformation of large span CFST arch bridge caused by temperature[J]. Journal of Chongqing Jiaotong University (Natural Science), 2008, 27(S): 843-848. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CQJT2008S1000.htm [27] 李秀梅, 赖炼, 谢肖礼. 钢管砼拱桥悬拼过程温度荷载对扣索偏角的影响[J]. 中南公路工程, 2004, 29(4): 29-30, 34. doi: 10.3969/j.issn.1674-0610.2004.04.007LI Xiu-mei, LAI Lian, XIE Xiao-li. Effect of temperature load on angular deflection in cantilever assembling construction of long span concrete filled steel arch bridge[J]. Central South Highway Engineering, 2004, 29(4): 29-30, 34. (in Chinese). doi: 10.3969/j.issn.1674-0610.2004.04.007 [28] 周倩, 周水兴, 李晓庆, 等. 混凝土拱桥悬臂浇筑施工力学性能研究[J]. 重庆交通大学学报(自然科学版), 2018, 37(7): 9-13, 68. doi: 10.3969/j.issn.1674-0696.2018.07.02ZHOU Qian, ZHOU Shui-xing, LI Xiao-qing, et al. Study on construction mechanical properties of cantilever-pouring concrete arch bridge[J]. Journal of Chongqing Jiaotong University (Natural Science), 2018, 37(7): 9-13, 68. (in Chinese). doi: 10.3969/j.issn.1674-0696.2018.07.02 [29] 韦建刚, 陈宝春. 钢管混凝土拱桥拱肋刚度设计取值分析[J]. 交通运输工程学报, 2008, 8(2): 38-43. http://transport.chd.edu.cn/article/id/201601004WEI Jian-gang, CHEN Bao-chun. Analysis on rib rigidity of concrete filled steel tubular arch bridge[J]. Journal of Traffic and Transportation Engineering, 2008, 8(2): 38-43. (in Chinese). http://transport.chd.edu.cn/article/id/201601004 [30] 吴庆雄, 陈宝春. 钢管混凝土拱桥桥面平整度评价[J]. 交通运输工程学报, 2010, 10(4): 23-28. doi: 10.3969/j.issn.1671-1637.2010.04.004WU Qing-xiong, CHEN Bao-chun. Deck roughness evaluation of concrete-filled steel tubular arch bridge[J]. Journal of Traffic and Transportation Engineering, 2010, 10(4): 23-28. (in Chinese). doi: 10.3969/j.issn.1671-1637.2010.04.004 [31] 杨绿峰, 解威威, 郑健, 等. 哑铃型钢管混凝土拱肋极限承载力的线弹性分析方法[J]. 交通运输工程学报, 2017, 17(3): 25-35. doi: 10.3969/j.issn.1671-1637.2017.03.003YANG Lyu-feng, XIE Wei-wei, ZHENG Jian, et al. Linear-elastic analysis method of ultimate bearing capacity of dumbbell-shaped CFST arch rib[J]. Journal of Traffic and Transportation Engineering, 2017, 17(3): 25-35. (in Chinese). doi: 10.3969/j.issn.1671-1637.2017.03.003 -





 下载:
下载: