简支梁桥上嵌入式轨道无缝线路可靠性分析

冯青松; 孙魁; 雷晓燕; 陈华鹏

doi:10.19818/j.cnki.1671-1637.2020.04.005

简支梁桥上嵌入式轨道无缝线路可靠性分析

doi: 10.19818/j.cnki.1671-1637.2020.04.005

华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013

基金项目:

国家自然科学基金项目 51878277

国家自然科学基金项目 51668020

江西省主要学科学术和技术带头人培养计划项目 20194BCJ22008

江西省重点研发计划项目 20192BBE50008

详细信息

作者简介:
冯青松(1978-), 男, 山西榆社人, 华东交通大学教授, 工学博士, 从事铁路环境振动与噪声和桥上无缝线路研究

通讯作者:
孙魁(1992-), 男, 安徽蚌埠人, 华东交通大学工学博士研究生

中图分类号: U213.2
计量
- 文章访问数: 1060
- HTML全文浏览量: 289
- PDF下载量: 681
- 被引次数: 0
出版历程
- 收稿日期: 2020-02-04
- 刊出日期: 2020-04-25

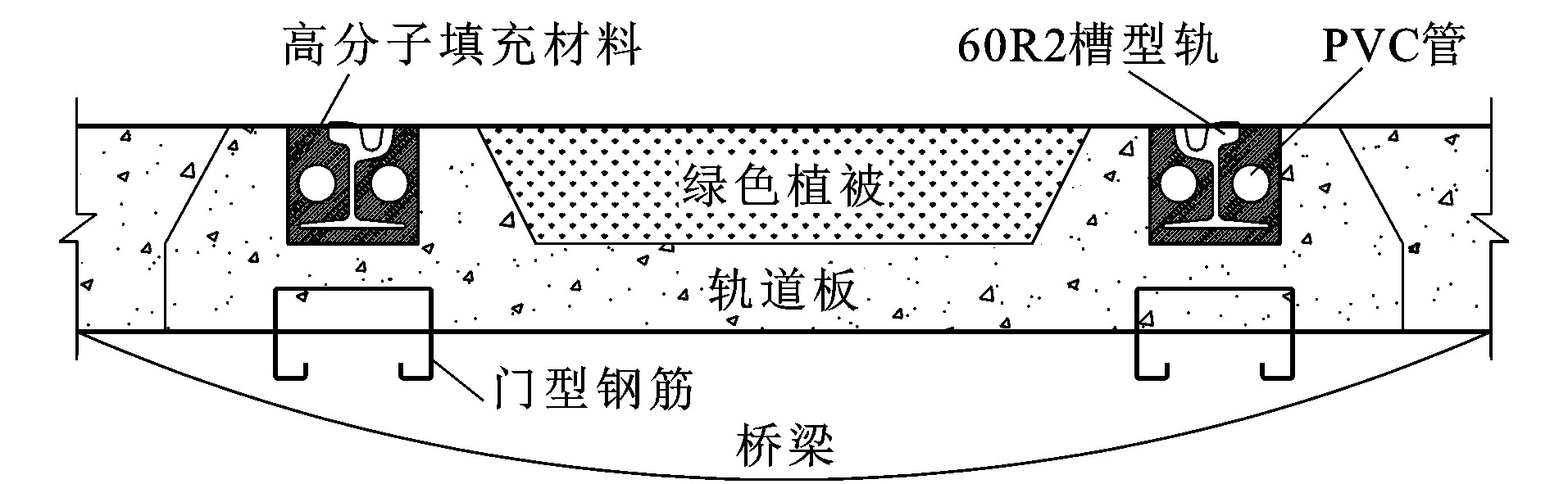
Reliability analysis of embedded track continuous welded rail on simply supported beam bridge

Engineering Research Center of Railway Environmental Vibration and Noise of Ministry of Education, East China Jiaotong University, Nanchang 330013, Jiangxi, China

Funds:

National Natural Science Foundation of China 51878277

National Natural Science Foundation of China 51668020

Training Plan for Academic and Technical Leaders of Major Disciplines of Jiangxi Province 20194BCJ22008

Key Research and Development Program of Jiangxi Province 20192BBE50008

More Information

Author Bio:
FENG Qing-song(1978-), male, professor, PhD, fqshdjtdx@aliyun.com

Corresponding author: SUN Kui(1992-), male, doctoral student, kui_sun@outlook.com

Article Text (Baidu Translation)

摘要

摘要: 为分析关键因素对桥上嵌入式轨道无缝线路力学特性的影响, 并基于可靠性理论对其进行评估, 采用有限元法建立了简支梁桥上嵌入式轨道无缝线路计算模型, 选择高分子材料纵向阻力和梁体温差为随机变量, 并根据实际工况确定了随机变量的分布类型和分布参数; 通过中心组合试验设计方法设计了响应面试验, 采用最小二乘法拟合了随机变量和响应之间的函数关系, 从而建立了轨板相对位移关于高分子材料纵向阻力和梁体温差的二次多项式响应面模型, 通过方差分析验证了所建立模型的正确性, 并采用灵敏度分析方法对随机变量进行了参数敏感性分析; 构建了桥上嵌入式轨道无缝线路长期服役性能的极限状态方程, 综合运用蒙特卡洛法和响应面模型评估了简支梁桥上嵌入式轨道无缝线路的可靠性。分析结果表明: 梁体温差和高分子材料纵向阻力对轨板相位移的灵敏度系数分别为0.99和-0.08, 梁体温差对轨板相对位移的影响远大于高分子材料纵向阻力; 在考虑参数的随机性以后, 温度作用下的轨板相对位移具有一定的离散性, 其主要分布在4.0~6.5 mm范围内, 且近似服从正态分布; 在不采取特殊处理措施的情况下, 不宜在年温差较大的地区建造桥上嵌入式轨道; 提出的桥上嵌入式轨道无缝线路可靠性评估方法可为嵌入式轨道结构的设计提供理论指导。
- 嵌入式轨道 /
- 无缝线路 /
- 响应面法 /
- 蒙特卡洛法 /
- 可靠性理论
Abstract: To analyze the influences of key factors on the mechanical characteristics of embedded track continuous welded rail on bridges, and evaluate it based on the reliability theory, the finite element method was used to establish the calculation model of embedded track continuous welded rail on the simply supported beam bridge. The longitudinal resistance of polymer material and the temperature difference of beam body were selected as the random variables, and the distribution types and distribution parameters of random variables were determined according to the actual working conditions. The response surface test was designed by the central composite test design method. The function relationship between the random variable and the response was fitted by the least square method. Thus, the quadratic polynomial response surface model of track-bridge relative displacement with respect to the longitudinal resistance of polymer material and the temperature difference of beam body was established. The correctness of the established model was verified by the variance analysis, and the parameter sensitivities of random variables were carried out through the sensitivity analysis method. The limit state equation of long-term service performance of embedded track continuous welded rail on bridges was constructed. The reliability of embedded track continuous welded rail on the simply supported beam bridge was comprehensively evaluated by using the Monte Carlo method and the response surface model. Analysis result shows that the sensitivity coefficients of temperature difference of beam body and longitudinal resistance of polymer material to the track-bridge relative displacement are 0.99 and-0.08, respectively. Therefore, the influence of temperature difference of beam body on the track-bridge relative displacement is much greater than that of the longitudinal resistance of polymer material. After considering the randomnesses of parameters, the track-bridge relative displacement under the action of temperature has a certain dispersion, mainly distributes in the range of 4.0-6.5 mm, and approximately follows the normal distribution. In the absence of special treatment measures, the embedded track on bridges should not be built in areas with large annual temperature difference. The proposed reliability evaluation method of embedded track continuous welded rail on bridges can provide a theoretical guidance for the design of embedded track structure.
- embedded track /
- continuous welded rail /
- response surface method /
- Monte Carlo method /
- reliability theory

HTML全文

图 1 嵌入式轨道示意

Figure 1. Schematic of embedded track

下载: 全尺寸图片幻灯片

图 2 计算模型示意

Figure 2. Schematic of calculation model

下载: 全尺寸图片幻灯片

图 3 A、B组填充材料

Figure 3. Filling materials of groups A and B

下载: 全尺寸图片幻灯片

图 4 极限状态示意

Figure 4. Schematic of limit state

下载: 全尺寸图片幻灯片

图 5 随机变量的概率密度分布

Figure 5. Probability density distributions of random variables

下载: 全尺寸图片幻灯片

图 6 轨板相对位移的概率密度分布

Figure 6. Probability density distribution of track-bridge relative displacement

下载: 全尺寸图片幻灯片

图 7 轨板相对位移的累积概率分布

Figure 7. Cumulative probability distribution of track-bridge relative displacement

下载: 全尺寸图片幻灯片

图 8 随机变量均值与桥上嵌入式轨道可靠度指标的关系

Figure 8. Relationships between mean values of random variables and reliability index

下载: 全尺寸图片幻灯片

图 9 随机变量变异系数与桥上嵌入式轨道可靠度指标的关系

Figure 9. Relationships between variation coefficients of random variables and reliability indexes of embedded track on bridges

下载: 全尺寸图片幻灯片

表 1 计算参数

Table 1. Calculation parameters

类别	参数	数值
60R2槽型轨	截面高度/cm	18
	弹性模量/GPa	210
	泊松比	0.3
	线膨胀系数/℃^-1	1.18×10^-5
	对水平轴的惯性矩/cm⁴	3 297
简支梁	弹性模量/GPa	35.5
	泊松比	0.2
	线膨胀系数/℃^-1	1.0×10^-5
	对水平轴的惯性矩/m⁴	0.99
	中性轴距上翼缘距离/m	0.71
	中性轴距下翼缘距离/m	0.99
桥墩	纵向刚度/(kN·cm^-1)	200
桥台	纵向刚度/(kN·cm^-1)	1 500

下载: 导出CSV

表 2 随机变量分布类型与分布参数

Table 2. Distribution types and distribution parameters of random variables

随机变量	分布类型与分布参数
高分子材料纵向阻力A	均值为17.5 kN·mm^-1, 标准差为2.5 kN·mm^-1, 变异系数为0.143的正态分布
梁体温差B	均值为32.5 ℃, 标准差为4.83 ℃, 变异系数为0.149的正态分布

下载: 导出CSV

表 3 因素水平

Table 3. Factor levels

因素	不同水平下的因素取值
因素	-2	-1	0	1	2
A/(kN·mm^-1)	10.0	12.2	17.5	22.8	25.0
B/℃	18.00	22.25	32.50	42.75	47.00

下载: 导出CSV

表 4 响应面试验

Table 4. Response surface test

试验点	1	2	3	4	5	6	7	8	9
A/(kN·mm^-1)	17.50	12.20	17.50	25.00	22.80	17.50	10.00	22.80	12.20
B/℃	32.50	42.75	18.00	32.50	22.25	47.00	32.50	42.75	22.25
轨板相对位移/mm	5.25	7.11	2.91	5.09	3.51	7.59	5.48	6.75	3.69

下载: 导出CSV

表 5 方差分析结果

Table 5. Variance analysis result

类别	平方和	自由度	均方值	F值	P值
响应面模型	23.060 0	5	4.440 0	54 533.600 0	< 0.000 1
A	0.150 0	1	0.150 0	1 829.380 0	< 0.000 1
B	22.040 0	1	22.040 0	270 700.000 0	< 0.000 1
AB	0.008 1	1	0.008 1	99.490 0	0.002 1
A²	0.000 8	1	0.000 8	10.180 0	0.049 7
B²	1.136 0×10^-6	1	1.136 0×10^-6	0.014 0	0.913 4
残差	0.000 2	3	8.141 0×10^-5
总模型	23.060 2	8

下载: 导出CSV

表 6 响应面模型误差分析结果

Table 6. Error analysis result of response surface model

响应	R²	R_a²
轨板相对位移	1.000 0	0.999 9

下载: 导出CSV

表 7 随机变量对轨板相位移的灵敏度

Table 7. Sensitivities of random variables to track-bridge relative displacement

随机变量		轨板相对位移
高分子材料纵向阻力	灵敏度	-0.08
高分子材料纵向阻力	灵敏度因子/%	7.15
梁体温差	灵敏度	0.99
梁体温差	灵敏度因子/%	92.85

下载: 导出CSV

表 8 桥上嵌入式轨道可靠度指标计算结果

Table 8. Calculation result of reliability index of embedded track on bridges

类别	失效概率	可靠度指标
轨板相对位移	2.92×10^-3	2.76

下载: 导出CSV

参考文献(32)

[1]	林红松, 颜华. 有轨电车埋入式无砟轨道及关键部件型式研究[J]. 铁道工程学报, 2016, 33(6): 60-65. doi: 10.3969/j.issn.1006-2106.2016.06.013 LIN Hong-song, YAN Hua. Type research on the embedded ballastless track structures and key components of modern tram way[J]. Journal of Railway Engineering Society, 2016, 33(6): 60-65. (in Chinese). doi: 10.3969/j.issn.1006-2106.2016.06.013
[2]	吴其刚. 现代有轨电车系统发展的重难点及对策研究[J]. 铁道工程学报, 2013, 30(12): 89-92, 98. doi: 10.3969/j.issn.1006-2106.2013.12.019 WU Qi-gang. Research on the emphasis and difficulties of modern tramcar system development and its countermeasures[J]. Journal of Railway Engineering Society, 2013, 30(12): 89-92, 98. (in Chinese). doi: 10.3969/j.issn.1006-2106.2013.12.019
[3]	LING Liang, HAN Jian, XIAO Xin-biao, et al. Dynamic behavior of an embedded rail track coupled with a tram vehicle[J]. Journal of Vibration and Control, 2016, 23(14): 2355-2372.
[4]	陈嵘, 马旭峰, 田春香, 等. 连续梁桥上单元板式无砟轨道纵向变形的控制[J]. 铁道工程学报, 2016, 33(1): 58-64. doi: 10.3969/j.issn.1006-2106.2016.01.012 CHEN Rong, MA Xu-feng, TIAN Chun-xiang, et al. Longitudinal deformation control of unit slab non-ballast track on continuous beam bridge[J]. Journal of Railway Engineering Society, 2016, 33(1): 58-64. (in Chinese). doi: 10.3969/j.issn.1006-2106.2016.01.012
[5]	RUGE P, BIRK C. Longitudinal forces in continuously welded rails on bridge decks due to nonlinear track-bridge interaction[J]. Computers and Structures, 2007, 85(7/8): 458-475.
[6]	TOTH J, RUGE P. Spectral assessment of mesh adaptations for the analysis of the dynamical longitudinal behaviour of railway bridges[J]. Archive of Applied Mechanics, 2001, 71(6/7): 453-462.
[7]	LIU Wen-shuo, DAI Gong-lian, HE Xu-hui. Sensitive factors research for track-bridge interaction of long-span X-style steel-box arch bridge on high-speed railway[J]. Journal of Central South University, 2013, 20(11): 3314-3323. doi: 10.1007/s11771-013-1855-6
[8]	冯青松, 孙魁, 徐金辉, 等. 桥梁温度分布情况对桥上无砟轨道的影响分析[J]. 铁道工程学报, 2018, 35(11): 20-26. doi: 10.3969/j.issn.1006-2106.2018.11.004 FENG Qing-song, SUN Kui, XU Jin-hui, et al. Study of influence of the bridge temperature distribution conditions on ballastless track on bridge[J]. Journal of Railway Engineering Society, 2018, 35(11): 20-26. (in Chinese). doi: 10.3969/j.issn.1006-2106.2018.11.004
[9]	王平, 刘浩, 魏贤奎, 等. 铁路斜拉桥上无缝线路纵向力规律分析[J]. 交通运输工程学报, 2013, 13(5): 27-32. doi: 10.3969/j.issn.1671-1637.2013.05.004 WANG Ping, LIU Hao, WEI Xian-kui, et al. Analysis of longitudinal force regulation for CWR on railway cable-stayed bridge[J]. Journal of Traffic and Transportation Engineering, 2013, 13(5): 27-32. (in Chinese). doi: 10.3969/j.issn.1671-1637.2013.05.004
[10]	王平, 谢铠泽. 连续刚构桥上无缝线路计算模型及方法的简化[J]. 中南大学学报(自然科学版), 2015, 46(7): 2735-2743. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201507048.htm WANG Ping, XIE Kai-ze. Simplification for calculation model and method of CWR on continuous rigid frame bridge[J]. Journal of Central South University (Science and Technology), 2015, 46(7): 2735-2743. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201507048.htm
[11]	MIN K H, YUN K M. An experimental study for longitudinal resistance of ballast track on bridge[J]. Journal of the Korea Academia-Industrial Cooperation Society, 2016, 17(5): 173-178. doi: 10.5762/KAIS.2016.17.5.173
[12]	戴公连, 朱俊樸, 闫斌. 30 t轴重重载铁路简支梁桥上无缝线路纵向力研究[J]. 土木工程学报, 2015, 48(8): 60-69. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201508010.htm DAI Gong-lian, ZHU Jun-pu, YAN Bin. Longitudinal force of continuous welded rail on simply-supported bridge under 30 t axle load heavy haul[J]. China Civil Engineering Journal, 2015, 48(8): 60-69. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201508010.htm
[13]	曲村, 高亮, 乔神路. 高速铁路长大桥梁CRTS Ⅰ型板式无砟轨道无缝线路力学特性分析[J]. 铁道标准设计, 2011(4): 12-16. doi: 10.3969/j.issn.1004-2954.2011.04.004 QU Cun, GAO Liang, QIAO Shen-lu. Analysis on dynamics property of CRTS Ⅰ ballastless track continuous line on long bridges of high speed railways[J]. Railway Standard Design, 2011(4): 12-16. (in Chinese). doi: 10.3969/j.issn.1004-2954.2011.04.004
[14]	曲村, 高亮, 乔神路, 等. 高速铁路长大桥梁CRTS Ⅰ型双块式无砟轨道无缝线路影响因素分析[J]. 铁道工程学报, 2011, 28(3): 46-51, 63. doi: 10.3969/j.issn.1006-2106.2011.03.009 QU Cun, GAO Liang, QIAO Shen-lu, et al. Analysis of influence factors on CRTS Ⅰ double-block ballastless track CWR on long-span bridge of high-speed railway[J]. Journal of Railway Engineering Society, 2011, 28(3): 46-51, 63. (in Chinese). doi: 10.3969/j.issn.1006-2106.2011.03.009
[15]	方利, 王志强, 李成辉. 简支梁桥上CRTS Ⅱ型板式无砟轨道制动力影响因素分析[J]. 铁道学报, 2012, 34(1): 72-76. doi: 10.3969/j.issn.1001-8360.2012.01.013 FANG Li, WANG Zhi-qiang, LI Cheng-hui. Analysis on influencing factors of braking force of CRTS Ⅱ ballastless track slab on simply-supported beam bridges[J]. Journal of the China Railway Society, 2012, 34(1): 72-76. (in Chinese). doi: 10.3969/j.issn.1001-8360.2012.01.013
[16]	张鹏飞, 桂昊, 雷晓燕, 等. 列车荷载下桥上CRTS Ⅲ型板式无砟轨道挠曲力与位移[J]. 交通运输工程学报, 2018, 18(6): 61-72. http://transport.chd.edu.cn/article/id/201806007 ZHANG Peng-fei, GUI Hao, LEI Xiao-yan, et al. Deflection force and displacement of CRTS Ⅲ slab track on bridge under train load[J]. Journal of Traffic and Transportation Engineering, 2018, 18(6): 61-72. (in Chinese). http://transport.chd.edu.cn/article/id/201806007
[17]	蔡小培, 高亮, 孙汉武, 等. 桥上纵连板式无砟轨道无缝线路力学性能分析[J]. 中国铁道科学, 2011, 32(6): 28-33. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201106006.htm CAI Xiao-pei, GAO Liang, SUN Han-wu, et al. Analysis on the mechanical properties of longitudinally connected ballastless track continuously welded rail on bridge[J]. China Railway Science, 2011, 32(6): 28-33. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201106006.htm
[18]	DAI Gong-lian, YAN Bin. Longitudinal forces of continuously welded track on high-speed railway cable-stayed bridge considering impact of adjacent bridges[J]. Journal of Central South University, 2012, 19(8): 2348-2353.
[19]	闫斌, 戴公连. 高速铁路斜拉桥上无缝线路纵向力研究[J]. 铁道学报, 2012, 34(3): 83-87. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201203019.htm YAN Bin, DAI Gong-lian. CWR longitudinal force of cable-stayed bridge of high-speed railway[J]. Journal of the China Railway Society, 2012, 34(3): 83-87. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201203019.htm
[20]	YAN Bin, DAI Gong-lian, ZHANG Hua-ping. Beam-track interaction of high-speed railway bridge with ballast track[J]. Journal of Central South University, 2012, 19(5): 1447-1453.
[21]	ZHANG Jiao-long, WU Deng-long, LI Qi. Loading-history-based track-bridge interaction analysis with experimental fastener resistance[J]. Engineering Structures, 2015, 83: 62-73.
[22]	李现博. 现代有轨电车嵌入式轨道结构桥上梁轨相互作用研究[D]. 成都: 西南交通大学, 2015. LI Xian-bo. Research on interaction between girder and track on modern trams bridge with the structure of embedded track[D]. Chengdu: Southwest Jiaotong University, 2015. (in Chinese).
[23]	胡燚斌. 地铁用嵌入式轨道桥上无缝线路研究[D]. 成都: 西南交通大学, 2017. HU Yi-bin. Studies of the continuously welded rail on bridge with embedded track for metro[D]. Chengdu: Southwest Jiaotong University, 2017. (in Chinese).
[24]	冯青松, 孙魁, 罗信伟, 等. 简支梁桥上嵌入式轨道无缝线路优化分析[J]. 华中科技大学学报(自然科学版), 2018, 46(5): 127-132. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201805023.htm FENG Qing-song, SUN Kui, LUO Xin-wei, et al. Optimization analysis on embedded track continuous welded rail on simple supported beam bridge[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(5): 127-132. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG201805023.htm
[25]	冯青松, 孙魁, 罗信伟, 等. 简支梁桥上有轨电车嵌入式轨道纵向力分析[J]. 铁道工程学报, 2017, 34(11): 27-32. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201711007.htm FENG Qing-song, SUN Kui, LUO Xin-wei, et al. Longitudinal force analysis of tram embedded track on simply supported bridge[J]. Journal of Railway Engineering Society, 2017, 34(11): 27-32. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201711007.htm
[26]	冯青松, 孙魁, 雷晓燕, 等. 连续梁桥上有轨电车嵌入式轨道伸缩力分析[J]. 铁道科学与工程学报, 2019, 16(1): 50-56. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201901007.htm FENG Qing-song, SUN Kui, LEI Xiao-yan, et al. Analysis of expansion-constriction force of tram embedded track on continuous beam bridge[J]. Journal of Railway Science and Engineering, 2019, 16(1): 50-56. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201901007.htm
[27]	谢铠泽, 赵维刚, 蔡小培, 等. 悬索桥初始内力与几何非线性对梁轨相互作用的影响[J]. 交通运输工程学报, 2020, 20(1): 82-91. doi: 10.19818/j.cnki.1671-1637.2020.01.006 XIE Kai-ze, ZHAO Wei-gang, CAI Xiao-pei, et al. Impacts of initial internal force and geometric nonlinearity of suspension bridge on bridge-rail interaction[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 82-91. (in Chinese). doi: 10.19818/j.cnki.1671-1637.2020.01.006
[28]	姜衡, 管贻生, 邱志成, 等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125-133. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201111019.htm JIANG Heng, GUAN Yi-sheng, QIU Zhi-cheng, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11): 125-133. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201111019.htm
[29]	梁淑娟. 长大桥上CRTS Ⅱ型板式无砟轨道断板影响与可靠性研究[D]. 北京: 北京交通大学, 2017. LIANG Shu-juan. Research on effects of broken plate damage and reliability of CRTSⅡ slab track on long-span bridge[D]. Beijing: Beijing Jiaotong University, 2017. (in Chinese).
[30]	YANG Dong-hui, LI Guo-ping, YI Ting-hua, et al. A performance-based service life design method for reinforced concrete structures under chloride environment[J]. Construction and Building Materials, 2016, 124: 453-461.
[31]	陈松坤, 王德禹. 基于神经网络的蒙特卡罗可靠性分析方法[J]. 上海交通大学学报, 2018, 52(6): 687-692. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201806011.htm CHEN Song-kun, WANG De-yu. An improved Monte Carlo reliability analysis method based on neural network[J]. Journal of Shanghai Jiaotong University, 2018, 52(6): 687-692. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201806011.htm
[32]	陈仁朋, 江朋, 叶肖伟, 等. 高铁单线路基循环累积变形分析方法及其可靠度分析[J]. 岩石力学与工程学报, 2016, 35(1): 141-149. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201601015.htm CHEN Ren-peng, JIANG Peng, YE Xiao-wei, et al. Analysis approach and reliability analysis of cumulative cyclic deformation of subgrade of single high-speed railway line[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1): 141-149. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201601015.htm