考虑时空修正的轨道交通封站短时客流预测方法

许心越; 吴宇航; 张英男; 王雪琴; 刘军

doi:10.19818/j.cnki.1671-1637.2021.05.021

考虑时空修正的轨道交通封站短时客流预测方法

doi: 10.19818/j.cnki.1671-1637.2021.05.021

1.
北京交通大学轨道交通控制与安全国家重点实验室，北京 100044
2.
武汉大学数学与统计学院，湖北武汉 430072
3.
东南大学数学学院，江苏南京 211189

基金项目:

国家自然科学基金项目 71871012

北京市自然科学基金项目 9212014

轨道交通控制与安全国家重点实验室自主研究课题 RCS2020ZT005

详细信息

作者简介:
许心越(1983-)，男，河南信阳人，北京交通大学副教授，工学博士，从事智能轨道交通系统研究

中图分类号: U293.13
计量
- 文章访问数: 998
- HTML全文浏览量: 384
- PDF下载量: 127
- 被引次数: 0
出版历程
- 收稿日期: 2021-05-21
- 网络出版日期: 2021-11-13
- 刊出日期: 2021-10-01

Short-term passenger flow forecasting method of rail transit under station closure considering spatio-temporal modification

1.
State Key Lab of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China
2.
School of Mathematics and Statistics, Wuhan University, Wuhan 430072, Hubei, China
3.
School of Mathematics, Southeast University, Nanjing 211189, Jiangsu, China

Funds:

National Natural Science Foundation of China 71871012

Beijing Natural Science Foundation 9212014

Independent Research Topic of State Key Lab of Rail Traffic Control and Safety RCS2020ZT005

More Information

Author Bio:
XU Xin-yue(1983-), male, associate professor, PhD, xxy@bjtu.edu.cn

Article Text (Baidu Translation)

摘要

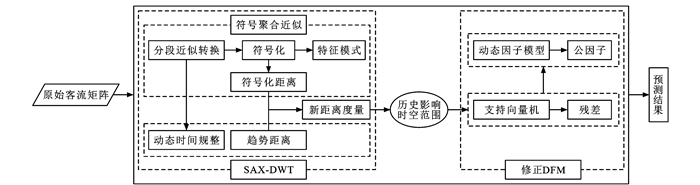
摘要: 为了实现封站情况下轨道交通短时客流的精准预测和探索客流的变化机理，提出了一种考虑时空修正的融合动态因子模型(DFM)和支持向量机(SVM)的短时客流预测方法(DFM-SVM); 利用符号聚合近似方法(SAX)与动态时间规整(DTW)相结合的算法(SAX-DTW)识别受封站影响的时空范围，利用DFM预测常态下的短时客流，利用SVM提取和处理受封站影响车站与时段客流量的非线性特征，对受影响车站与时段的客流量进行修正; 以北京地铁封站情景下车站的进站量预测为例，验证方法的有效性。研究结果表明: 与既有SAX相比，提出的SAX-DTW不仅能全面考虑到客流数量和客流趋势的变化，还能更准确地识别出多个车站的异常时段; 与传统DFM相比，DFM-SVM能显著降低各车站的预测残差，其中奥体中心车站的预测残差降低约60%;与基线模型霍尔特-温特(Holt-Winters)、SVM、门控循环单元(GRU)和长短期记忆(LSTM)相比，在整体客流量预测效果方面，提出的DFM-SVM在其均方根误差方面分别降低43.39%、70.00%、33.18%和70.83%，平均绝对误差分别降低43.72%、67.17%、28.98%和57.08%;在单个车站的客流量预测效果方面，提出的DFM-SVM在均方根误差和平均绝对误差方面有70%的车站均低于其他基准模型。可见，提出的DFM-SVM能够捕捉封站影响客流的非线性关系，极大提升了客流预测精度，能够为运营管理者提供可靠的客流预警信息与决策依据。
- 轨道交通 /
- 封站 /
- 短时客流预测 /
- 封站范围识别 /
- 动态因子模型 /
- 客流时空修正
Abstract: To realize the accurate prediction of the short-term passenger flow of rail transit and explore the changing mechanism of passenger flow under the station closure, a short-term spatio-temporal corrected passenger flow forecasting method considering dynamic factor model (DFM) and support vector machine (SVM) under the station closure was developed and denoted by DFM-SVM. A hybrid model combining symbolic aggregation approximation (SAX) and dynamic time warping (DTW) denoted by SAX-DTW was proposed to identify the spatio-temporal ranges of the affected stations. DFM was developed to forecast the short-term passenger flow under the normal scenario based on the historical data. SVM was developed to extract and process the nonlinear characteristics of the passenger flows at the affected stations and time periods and used to correct the correspondingly affected passenger flows. The validity of the method was verified by an example of the inbound volume prediction at the Beijing Subway Station under the station closure. Research results show that compared with the SAX, the proposed SAX-DFM not only comprehensively considers the changes in the number and trend of passenger flow, but also identifies the abnormal segments of several stations according to the case study more accurately. Compared with the traditional DFM, the proposed DFM-SVM can significantly reduce the forecasting residual errors of passenger flows at each station. Taking the Olympic Sports Center Station as an example, the residual error reduces by about 60%. In terms of overall passenger flow prediction of the whole stations, the proposed DFM-SVM reduces the root mean square errors by 43.39%, 70.00%, 33.18% and 70.83%, respectively, and the mean absolute errors by 43.72%, 67.17%, 28.98% and 57.08%, respectively, compared with the baseline models such as Holt-Winters, SVM, gate recurrent unit (GRU), and long short-term memory (LSTM). In terms of the passenger volume prediction at a single station, the proposed DFM-SVM can reduce the root mean square errors and mean absolute errors at about 70% stations compared with other benchmark models. Therefore, the proposed DFM-SVM can capture the nonlinear feature of passenger flow affected by the station closure, which greatly improves the prediction accuracy and provides reliable passenger flow's early warning information and decision-making basis for operation managers. 4 tabs, 9 figs, 30 refs.
- rail transit /
- station closure /
- short-term passenger flow forecasting /
- range identification under station closure /
- dynamic factor model /
- passenger flow spatio-temporal modification

HTML全文

图 1 模型框架

Figure 1. Model framework

下载: 全尺寸图片幻灯片

图 2 受封站影响的车站

Figure 2. Stations affected by station closure

下载: 全尺寸图片幻灯片

图 3 北沙滩站进站客流符号化对比

Figure 3. Comparison of inbound symbolic passenger flows at North Beach Station

下载: 全尺寸图片幻灯片

图 4 奥体中心站第7时段进站量

Figure 4. Inbound passenger flows at Olympic Sports Station in 7th period

下载: 全尺寸图片幻灯片

图 5 森林公园南门站第1、2时段进站量

Figure 5. Inbound passenger flows at Forest Park South Gate Station in 1st and 2nd periods

下载: 全尺寸图片幻灯片

图 6 公共因子变化趋势

Figure 6. Changing trends of common factors

下载: 全尺寸图片幻灯片

图 7 封站时段安立路站客流量预测结果

Figure 7. Prediction result of passenger flow at Anli Road Station during station closure

下载: 全尺寸图片幻灯片

图 8 奥体中心站客流量预测结果

Figure 8. Prediction result of passenger flow at Olympic Sports Center Station

下载: 全尺寸图片幻灯片

图 9 北沙滩站客流量预测结果

Figure 9. Prediction result of passenger flow at North Beach Station

下载: 全尺寸图片幻灯片

表 1 封站影响范围识别结果

Table 1. Identification result of influence range under station closure

模型	安立路站	奥体中心站	北沙滩站	北土城站	霍营站	林萃桥站	六道口站	森林公园南门站	永泰庄站	育新站
SAX	0.13	0.01	0.05	0.13	0.00	0.04	0.12	0.25	0.07	0.16
	0.31	0.10	0.10	0.00	0.01	0.08	0.17	0.24	0.03	0.05
	0.04	0.44	0.04	0.04	0.01	0.10	0.02	0.26	0.11	0.22
	0.05	0.08	0.11	0.02	0.01	0.07	0.01	0.05	0.00	0.03
	0.01	0.25	0.06	0.00	0.01	0.07	0.01	0.05	0.02	0.04
	0.13	0.26	0.05	0.32	0.04	0.13	0.26	0.39	0.03	0.14
	0.18	0.01	0.23	0.28	0.01	0.17	0.14	0.28	0.03	0.01
	0.04	1.16	0.02	0.13	0.01	0.04	0.11	0.78	0.01	0.08
SAX-DTW	0.52	0.15	0.37	0.25	0.04	0.96	0.27	0.57	0.26	0.25
	0.96	0.28	2.11	2.21	0.55	2.41	1.13	0.67	0.99	2.18
	0.35	5.33	0.44	0.15	0.04	0.30	0.15	2.14	0.21	0.39
	0.21	0.56	0.46	0.18	0.01	0.21	0.37	0.38	0.10	0.08
	0.29	1.19	0.28	0.30	0.02	0.42	0.22	0.83	0.10	0.10
	2.41	2.99	1.66	2.44	0.14	1.54	1.72	3.38	0.25	0.41
	0.75	13.30	1.37	2.17	0.01	4.15	1.18	4.30	0.25	0.16
	0.14	20.32	0.29	0.57	0.01	0.58	0.65	4.75	0.06	0.11

下载: 导出CSV

表 2 因子载荷矩阵

Table 2. Factor loading matrix

车站	临近车站因子	间隔车站因子	周围换乘车站因子
安立路站	0.26	-0.10	-0.14
奥体中心站	0.08	-0.12	-0.15
北沙滩站	0.22	-0.20	-0.16
北土城站	0.11	0.35	-0.16
霍营站	-0.14	0.10	-0.26
林萃桥站	0.25	0.14	0.17
六道口站	0.27	0.10	-0.04
森林公园南门站	0.14	0.00	0.18
永泰庄站	-0.07	0.31	-0.11
育新站	-0.14	0.08	-0.27

下载: 导出CSV

表 3 模型预测精度对比

Table 3. Comparison of models' prediction accuracies

车站	DFM			基于SAX的修正DFM			DFM-SVM
车站	E₁/ [人次·(5 min)^-1]	E₂	E₃/ [人次·(5 min)^-1]	E₁/ [人次·(5 min)^-1]	E₂	E₃/ [人次·(5 min)^-1]	E₁/ [人次·(5 min)^-1]	E₂	E₃/ [人次·(5 min)^-1]
安立路站	10.35	0.23	8.16	10.11	0.23	7.95	9.99	0.23	7.88
奥体中心站	10.43	0.62	7.88	9.63	0.60	7.42	9.45	0.59	7.27
北沙滩站	10.84	0.26	8.09	10.66	0.25	7.88	10.18	0.25	7.64
北土城站	10.33	0.33	7.99	10.37	0.33	8.03	10.18	0.33	7.90
霍营站	38.42	0.42	26.15	38.42	0.42	26.15	38.42	0.42	26.15
林萃桥站	11.18	0.40	8.76	10.97	0.38	8.39	10.95	0.38	8.40
六道口站	11.25	0.24	8.33	11.00	0.23	7.99	10.34	0.23	7.60
森林公园南门站	15.89	0.57	11.96	15.51	0.54	11.57	14.74	0.54	11.26
永泰庄站	12.93	0.22	9.61	12.67	0.22	9.34	12.59	0.22	9.28
育新站	16.88	0.31	11.68	16.39	0.30	11.14	15.81	0.30	10.53

下载: 导出CSV

表 4 模型预测精度对比

Table 4. Comparison of prediction accuracies among models

方法	指标	安立路站	奥体中心站	北沙滩站	北土城站	霍营站	林萃桥站	六道口站	森林公园南门站	永泰庄站	育新站	均值
DFM-SVM	E₁/[人次·(5 min)^-1]	9.99	9.45	10.18	10.18	38.42	10.95	10.34	14.74	12.59	15.81	14.26
	E₂	0.23	0.59	0.25	0.33	0.42	0.38	0.23	0.54	0.22	0.30	0.35
	E₃/[人次·(5 min)^-1]	7.88	7.27	7.64	7.90	26.15	8.40	7.60	11.26	9.28	10.53	10.39
Holt-Winters	E₁/[人次·(5 min)^-1]	16.65	25.34	15.48	21.39	73.95	16.74	19.43	15.88	19.91	27.12	25.19
	E₂	0.56	0.43	0.50	0.95	0.86	0.53	0.49	0.35	0.50	1.04	0.62
	E₃/[人次·(5 min)^-1]	12.57	15.62	11.51	15.87	53.15	12.07	15.87	11.02	15.34	21.56	18.46
SVM	E₁/[人次·(5 min)^-1]	25.67	20.63	23.34	26.15	205.44	21.31	29.86	15.98	51.56	55.47	47.54
	E₂	0.29	0.78	0.33	0.44	0.63	0.41	0.33	0.64	0.53	0.55	0.49
	E₃/[人次·(5 min)^-1]	16.59	15.69	14.85	17.13	141.14	13.75	19.11	10.11	31.86	36.34	31.65
GRU	E₁/[人次·(5 min)^-1]	16.78	15.88	15.86	20.29	44.10	20.48	19.85	13.40	22.12	24.63	21.34
	E₂	0.20	0.33	0.24	0.24	0.25	0.43	0.23	0.33	0.21	0.22	0.27
	E₃/[人次·(5 min)^-1]	12.25	12.08	11.42	14.02	25.76	14.43	14.74	9.22	15.28	17.05	14.63
LSTM	E₁/[人次·(5 min)^-1]	17.39	15.46	17.27	20.89	282.92	20.58	18.30	12.40	40.82	42.87	48.89
	E₂	0.27	0.54	0.33	0.33	0.42	0.44	0.24	0.37	0.26	0.31	0.35
	E₃/[人次·(5 min)^-1]	12.14	10.55	13.17	12.76	113.04	13.75	12.92	8.49	22.79	22.50	24.21

下载: 导出CSV

参考文献(30)

[1]	叶红霞. 突发事件下城市轨道交通网络客流重分布预测方法研究与应用[J]. 城市轨道交通研究, 2018, 21(8): 63-66. https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201808015.htm YE Hong-xia. On the prediction method of passenger flow redistribution under urban rail transit network emergency[J]. Urban Mass Transit, 2018, 21(8): 63-66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDJT201808015.htm
[2]	NOURSALEHI P, KOUTSOPOULOS H N, ZHAO Jin-hua. Real time transit demand prediction capturing station interactions and impact of special events[J]. Transportation Research Part C: Emerging Technologies, 2018, 97: 277-300. doi: 10.1016/j.trc.2018.10.023
[3]	LI Yang, WANG Xu-dong, SUN Shuo, et al. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks[J]. Transportation Research Part C: Emerging Technologies, 2017, 77: 306-328. doi: 10.1016/j.trc.2017.02.005
[4]	LAÑA I, LOBO J L, CAPECCI E, et al. Adaptive long-term traffic state estimation with evolving spiking neural networks[J]. Transportation Research Part C: Emerging Technologies, 2019, 101: 126-144. doi: 10.1016/j.trc.2019.02.011
[5]	张丽英, 孟斌, 尹芹. 基于符号集合近似的城市轨道交通站点分类研究[J]. 地球信息科学学报, 2016, 18(12): 1597-1607. https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX201612005.htm ZHANG Li-ying, MENG Bin, YIN Qin. Classification of urban rail transit stations based on SAX[J]. Journal of Geo-Information Science, 2016, 18(12): 1597-1607. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQXX201612005.htm
[6]	LKHAGVA B, SUZUKI Y, KAWAGOE K. New time series data representation ESAX for financial applications[C]//IEEE. Proceedings of the 22nd International Conference on Data Engineering Workshops. New York: IEEE, 2006: 17-22.
[7]	ZHANG Ke, LI Yuan, CHAI Yi, et al. Trend-based symbolic aggregate approximation for time series representation[C]// IEEE. The 30th Chinese Control and Decision Conference. New York: IEEE, 2018: 2234-2240.
[8]	YAHYAOUI H, AL-DAIHANI R. A novel trend based SAX reduction technique for time series[J]. Expert Systems with Applications, 2019, 130: 113-123. doi: 10.1016/j.eswa.2019.04.026
[9]	RUAN Hui, HU Xiao-guang, XIAO Jin, et al. TrSAX—an improved time series symbolic representation for classification[J]. ISA Transactions, 2020, 100: 387-395. doi: 10.1016/j.isatra.2019.11.018
[10]	HONG J Y, PARK S H, BAEK J G. SSDTW: shape segment dynamic time warping[J]. Expert Systems with Applications, 2020, 150(3): 113291.
[11]	ZHAO Jian-ping, ITTI L. ShapeDTW: shape dynamic time warping[J]. Pattern Recognition, 2018, 74: 171-184. doi: 10.1016/j.patcog.2017.09.020
[12]	PEREIRA F C, RODRIGUES F, BEN-AKIVA M. Using data from the web to predict public transport arrivals under special events scenarios[J]. Journal of Intelligent Transportation Systems, 2015, 19(3): 273-288. doi: 10.1080/15472450.2013.868284
[13]	SILVA R, KANG S M, AIROLDI E M. Predicting traffic volumes and estimating the effects of shocks in massive transportation systems[J]. PNAS, 2015, 112(18): 5643-5648. doi: 10.1073/pnas.1412908112
[14]	MA Tao, ZHOU Zhou, ANTONIOU C. Dynamic factor model for network traffic state forecast[J]. Transportation Research Part B: Methodological, 2018, 118: 281-317. doi: 10.1016/j.trb.2018.10.018
[15]	CHEN En-hui, YE Zhi-rui, WANG Chao, et al. Subway passenger flow prediction for special events using smart card data[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(3): 1109-1120. doi: 10.1109/TITS.2019.2902405
[16]	MA Tao, ANTONIOU C, TOLEDO T. Hybrid machine learning algorithm and statistical time series model for network-wide traffic forecast[J]. Transportation Research Part C: Emerging Technologies, 2020, 111: 352-372. doi: 10.1016/j.trc.2019.12.022
[17]	TAO Yu-xin, YAN Hai-rong, GAO Hang, et al. Application of SVR optimized by modified simulated annealing (MSA-SVR) air conditioning load prediction model[J]. Journal of Industrial Information Integration, 2019, 15: 247-251. doi: 10.1016/j.jii.2018.04.003
[18]	SUN Yi-xin, LENG Biao, GUAN Wei. A novel wavelet- SVM short-time passenger flow prediction in Beijing subway system[J]. Neurocomputing, 2015, 166: 109-121. doi: 10.1016/j.neucom.2015.03.085
[19]	姚智胜, 邵春福, 高永亮. 基于支持向量回归机的交通状态短时预测方法研究[J]. 北京交通大学学报, 2006, 30(3): 19-22. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT200603004.htm YAO Zhi-sheng, SHAO Chun-fu, GAO Yong-liang. Research methods of short-term traffic forecasting based on support vector regression[J]. Journal of Beijing Jiaotong University, 2006, 30(3): 19-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT200603004.htm
[20]	米根锁, 赵丽琴, 罗淼. GCPSO优化混合核SVM的地铁车站客流预测[J]. 计算机工程与应用, 2015, 51(14): 231-235, 270. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201514044.htm MI Gen-suo, ZHAO Li-qin, LUO Miao. Subway station passenger flow forecast based on mixed kernel support vector machine optimized by golden section chaotic particle swarm optimization[J]. Computer Engineering and Applications, 2015, 51(14): 231-235. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201514044.htm
[21]	杨军, 侯忠生. 基于小波分析的最小二乘支持向量机轨道交通客流预测方法[J]. 中国铁道科学, 2013, 34(3): 122-127. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201303021.htm YANG Jun, HOU Zhong-sheng. A wavelet analysis based LS-SVM rail transit passenger flow prediction method[J]. China Railway Science, 2013, 34(3): 122-127. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201303021.htm
[22]	TANG Li-yang, ZHAO Yang, CABRERA J, et al. Forecasting short-term passenger flow: an empirical study on Shenzhen Metro[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10): 2613-2622.
[23]	LIN J, KEOGH E, LONARDI S, et al. A symbolic representation of time series, with implications for streaming algorithms[C]//Association for Computing Machinery. Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery. New York: Association for Computing Machinery, 2003: 2-11.
[24]	SAKOE H. Two-level DP-matching—a dynamic programming- based pattern matching algorithm for connected word recognition[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1979, ASSP-27(6): 588-595.
[25]	奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(3): 123-124, 128. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201103038.htm FENG Guo-he. Parameter optimizing for support vector machines classification[J]. Computer Engineering and Applications, 2011, 47(3): 123-124, 128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG201103038.htm
[26]	DOZ C, GIANNONE D, REICHLIN L. A quasi-maximum likelihood approach for large approximate dynamic factor models[J]. The Review of Economics and Statistics, 2012, 94(4): 1014-1024.
[27]	BAI Ju-shan, LI Kun-peng. Maximum likelihood estimation and inference for approximate factor models of high dimension[J]. The Review of Economics and Statistics, 2016, 98(2): 298-309.
[28]	汪选胜. 改进的三次指数平滑模型在交通优化中的研究与应用[J]. 机械制造与自动化, 2012, 41(4): 18-20. https://www.cnki.com.cn/Article/CJFDTOTAL-ZZHD201204006.htm WANG Xuan-sheng. Research on improved cubic exponential smooth model in traffic optimization and its application[J]. Machine Building and Automation, 2012, 41(4): 18-20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZZHD201204006.htm
[29]	TOQUÉ F, CỘME E, EL MAHRSI M K, et al. Forecasting dynamic public transport origin-destination matrices with long-short term memory recurrent neural networks[C]//IEEE. IEEE 19th International Conference on Intelligent Transportation Systems. New York: IEEE, 2016: 1071-1076.
[30]	WU Yu-hang, HUANG Bao-jing, LI Xue, et al. A data-driven approach to detect passenger flow anomaly under station closure[J]. IEEE Access, 2020, 8: 149602-149615.