Sensitivity analysis of high-speed train wheel vibration influenced by vehicle-track coupling
-
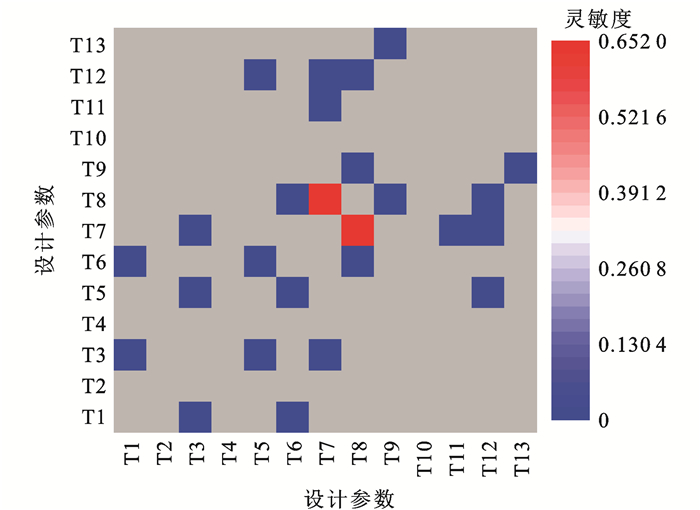
摘要: 考虑车辆一系、二系悬挂参数和轨道参数的随机性,在多体动力学软件UM当中建立了CRH2动车组拖车的随机性仿真模型;采用最优拉丁超立方试验设计方法抽取车辆参数和轨道参数的随机样本,利用多目标优化软件iSight调用随机样本,联合UM完成了随机样本仿真分析;在有限试验设计样本和仿真数据的限制下,以最佳近似精度为目标,结合最小角回归、低阶交互截断和留一法交叉验证等实现了多项式混沌展开,构建多项式混沌展开代理模型;采用Sobol法进行全局灵敏度分析,研究了直线、曲线2种工况下车辆参数和轨道参数随机耦合作用对于车轮振动特性的影响,找出了主要影响因子,并考虑了多参数之间的交互效应。研究结果表明:多项式混沌展开法能够基于已有的样本比较好地拟合出代理模型,计算出Sobol灵敏度系数,平均误差低于3%,从而可以高效、定量地分析各参数耦合作用对车轮振动的影响;转臂节点横向刚度、一系弹簧垂向刚度、一系弹簧横向刚度和二系横向减振器阻尼是对车轮振动响应方差具有较大贡献的车辆参数,轨道横向、垂向刚度是对车轮振动响应方差具有较大贡献的轨道参数,各参数之间存在明显交互效应。
-
关键词:
- 车轮振动 /
- 多项式混沌展开代理模型 /
- Sobol法 /
- 全局灵敏度分析 /
- 交互效应
Abstract: A random simulation model for one trailer of the CRH2 EMU was established based on the multi-body dynamics software UM under considering the randomness of the primary and secondary suspension parameters of the vehicle and track parameters. The optimal Latin hypercube experimental design method was used to extract the random samples of the parameters, the multi-objective optimization software iSight was used to select the random samples, and the UM was used to analyze the samples. Under the limitation of limited experimental design samples and simulation data, a polynomial chaos expansion surrogate model was built by combining the minimum angle regression, low-order interactive truncation and leave-one-out cross-validation to achieve the polynomial chaos expansion in order to reach the best approximate accuracy. The Sobol method was used to analyze the global sensitivity of polynomial chaos expansion surrogate model to study the influence of the random coupling action of vehicle and track parameters on the wheel vibration characteristics under the straight line and curve working conditions. The key factors were studied and the coupling action of multi-parameters was considered. The results show that the polynomial chaos expansion method can fit an accurate surrogate model based on the existing samples and calculate the Sobol sensitivity coefficient with an average error (less than 3%) so as to analyze the effect of the coupling of various parameterss on the wheel vibration efficiently and quantitatively. The vehicle parameters, such as the lateral stiffness of the boom node, the vertical stiffness of the primary spring, the lateral stiffness of the primary spring and the damping of the secondary transverse shock absorber, have an obvious contribution to the variance of the wheel vibration response. The track parameters, such as the lateral and vertical stiffnesses of the track, have a large contribution to the variance of the wheel vibration response. There are obvious interaction effects between the various parameters. 2 tabs, 16 figs, 31 refs. -
0. 引言
近年来, 随着人们对运输高效的追求, 中国高速铁路及高速列车技术发展迅速。2016年7月, 《中长期铁路网规划》发布, 提出构筑“八纵八横”高速铁路主通道, 拓展区域铁路连接线, 发展城际客运铁路。规划中的“八纵八横”高速铁路大部分处于季风区, 而季风区年降水量在400 mm以上。降雨改变了高速列车周围流场的物质构成, 列车运行不仅受到空气的作用, 还受到雨滴的撞击作用, 形成空气、雨滴与列车之间复杂的相互作用。国内外学者在高速列车空气动力学方面已经开展了大量的研究工作, 通过风洞试验和数值仿真方法分析了车速、风速、线路等因素对高速列车的流场特性、气动力特性及运行安全特性的影响[1-6], 发现高速列车的气动效应显著, 尤其当处于恶劣运行工况下, 如环境风、高架桥、高堤坝等, 列车的气动性能急剧恶化, 严重威胁列车的运行安全。降雨是非常常见的一种自然现象, 雨滴在降落过程中, 会对运行中的列车产生冲击作用, 使得高速列车的气动性能进一步恶化, 因此, 非常有必要研究降雨对高速列车气动性能的影响。
目前有关降雨对结构的影响研究主要集中在飞机和建筑领域[7-12]。20世纪80年代起, 人们开始关注强风雨对高速运动物体气动性能的影响。美国NASA自1985年开始启动一个持续性研究项目, 采用风洞试验方法研究了降雨对飞机气动性能的影响[7]。降雨对运动物体的影响本质上属于气-液两相流问题, 常用的数值模拟方法包括Euler-Lagrange方法和Euler-Euler方法。Euler-Lagrange方法将雨滴视为离散相颗粒, 采用时间平均的Navier-Stokes方程来求解连续相空气的控制方程, 并建立雨滴的Lagrange运动方程, 追踪雨滴运动轨迹; Euler-Euler方法将连续相空气和离散相雨滴均视为连续介质, 采用时间平均的Navier-Stokes方程求解空气和雨滴的流动控制方程。Wu等采用Euler-Lagrange方法数值模拟了强降雨环境下机翼的气动特性, 数值仿真结果与试验结果吻合较好[8]; Huang等基于Euler-Euler方法研究了建筑物的风驱雨强, 得到降雨对建筑物的冲击载荷[9]。
近年来, 降雨对高速列车空气动力学特性的影响已经引起了学者们的关注。司天文通过理论分析推导了风雨共同作用时的风驱雨强表达式, 计算了风驱雨强作用下雨滴对列车的冲击力, 并建立了列车临界倾覆时的受力平衡方程, 得到了不同雨强作用下列车的临界倾覆风速[13]; 李军产采用Euler-Lagrange方法研究了风雨联合作用下高速列车中间段车辆的周围流场分布及气动力特性[14]; 张淼利用Euler-Lagrange方法分析了雨滴与列车的主要碰撞位置及雨滴颗粒的主要聚集区域, 指出列车在降雨中运行的气动性能变化主要与车速、运行工况及降雨强度有关[15]; 敬俊娥等利用Euler-Lagrange方法研究了风雨作用下的列车空气动力学特性, 发现降雨的存在使得列车所受的气动载荷有所增大, 与无雨时相比, 当降雨强度为100 mm·h-1时, 车辆受到的横向力、升力和倾覆力矩分别增加约3.0%、4.4%和3.3%[16]; 倪守隆采用Euler-Lagrange方法对高速列车在风雨场中的运行进行了数值模拟, 研究了降雨天气下横风风场对列车气动特性的影响[17]; Shao等利用Euler双流体模型针对60 mm·h-1的降雨强度, 研究了降雨和环境风联合作用下列车的气动性能和运行稳定性, 发现降雨使列车的气动性能恶化, 极限运行车速降低10%~20%[18]; 岳煜斐等利用Euler-Euler方法对风雨作用下的列车气动特性进行研究, 发现受降雨影响, 列车所受的阻力、侧力及倾覆力矩均增大[19]; Nestor采用Euler-Euler方法研究了强风雨下高速列车的表面压力、横截面流速及气动力(矩), 发现与无降雨相比, 降雨使列车的气动力和气动力矩均增大, 增加了列车的脱轨风险[20]; 孙自豹等利用Euler-Lagrange方法分别模拟了均匀雨相和雨滴Gamma谱对高速列车气动性能的影响, 发现在Gamma谱降雨条件下, 列车气动特性受车速影响较大[21]。
通过以上分析, 目前降雨(包括风雨)对高速列车空气动力学特性的影响研究尚处于起步阶段, 以往的研究所采用的列车模型通常忽略转向架和风挡等局部结构, 而这些局部结构可能会对列车周围流场产生影响。此外, 以往的研究对数值计算模型准确性的探讨也较少, 且通常针对特定的降雨强度或列车速度, 没有系统获得气动力系数随降雨强度及列车速度的变化规律。为此, 本文建立包括转向架和风挡等局部结构的列车模型, 采用Euler-Lagrange方法建立降雨环境下高速列车空气动力学计算模型, 并通过与试验数据对比, 验证列车空气动力学计算的准确性及降雨环境模拟的可靠性; 在此基础上, 开展降雨环境下高速列车的空气动力学计算, 研究车速、降雨强度及雨滴粒径对高速列车空气动力学性能的影响。
1. 计算方法
1.1 连续相
通常情况下, 高速列车明线运行气动性能计算可以采用不可压缩定常流[22-23]。与高速列车相关的流动现象绝大多数是湍流流动, 工程湍流计算通常采用的方法是基于雷诺时均方程的湍流模型方法。由此, 高速列车绕流流场控制方程为定常不可压缩雷诺时均Navier-Stokes方程, 其表达式如下[8]
∂-uj∂xj=0 (1)ρ∂(-uj-ui)∂xj=-∂-p∂xi+∂-τij∂xj+ ∂∂xj(-ρ¯u′iu′j)-Μi (2)
式中: -uj为空气速度第j个分量的时间平均值, j=1, 2, 3, 分别对应纵向、横向、垂向3个方向; xj为直角坐标第j个分量; ρ为空气密度; -ui为空气速度第i个分量的时间平均值, i=1, 2, 3, 分别对应纵向、横向、垂向3个方向; -p为空气压力的时间平均值; xi为直角坐标第i个分量; -τij为黏性应力张量的时间平均值; -ρ¯u′iu′j为雷诺应力, u′i为空气速度第i个分量的脉动值, u′j为空气速度第j个分量的脉动值; Mi为相间动量交换第i个分量。
本文湍流模型采用SST κ-ω模型(κ为湍动能; ω为湍流频率)。SST κ-ω模型是建立在标准κ-ω模型和标准κ-ε(ε为湍动能耗散率)模型基础上, 在边界层内部采用标准κ-ω模型, 在边界层外部采用高雷诺数的κ-ε模型, 且在边界层内部和外部能够逐渐过渡, 因此, SST κ-ω模型在广泛的流动领域中有更高的精度和可信度[24], 其表达式如下
ρ∂(κ-ui)∂xi=∂∂xj(Γκ∂κ∂xj)+Gκ-Yκ (3) ρ∂(ω-ui)∂xi=∂∂xj(Γω∂ω∂xj)+Gω-Yω+Dω (4)
式中: Γκ为κ的扩散率; Γω为ω的扩散率; Gκ为κ的湍流生成项; Gω为ω的湍流生成项; Yκ为κ的湍流耗散项; Yω为ω的湍流耗散项; Dω为交叉扩散项。
高速列车空气动力学性能参数主要是气动阻力系数和气动升力系数, 定义为
CD=FD0.5ρAV2 (5)CL=FL0.5ρAV2 (6)
式中: CD为气动阻力系数; CL为气动升力系数; FD为气动阻力; FL为气动升力; A为参考面积, 通常取车体断面面积; V为列车速度。
列车气动阻力是列车表面压力和切应力沿列车阻力方向的合力, 气动升力是列车表面压力和切应力沿列车升力方向的合力, 其表达式分别为
FD=∮S(pD+τD)dS (7)FL=∮S(pL+τL)dS (8)
式中: S为列车外表面积; pD为列车表面压力在列车阻力方向上的分量; pL为列车表面压力在列车升力方向上的分量; τD为列车表面切应力在列车阻力方向上的分量; τL为列车表面切应力在列车升力方向上的分量。
1.2 离散相
采用Lagrange方法对离散相雨滴进行模拟。建模时, 假设雨滴是球形的, 只考虑空气阻力和重力的作用, 而不考虑雨滴之间的相互作用, 且假设雨滴不会发生变形。在Lagrange参考框架下, 雨滴运动方程[24]为
dupidt=18μρpd2pcRep24(ui-upi)+ gi(ρp-ρ)ρp (9)
式中: upi为雨滴速度第i个分量; t为时间; μ为动力黏度; ρp为雨滴密度; dp为雨滴粒径; c为雨滴曳力系数; Rep为相对雷诺数; ui为空气速度的第i个分量; gi为重力加速度第i个分量。
球形颗粒的曳力系数[25]计算公式为
c=a1+a2Rep+a3Re2p (10)
式中: a1、a2、a3为经验系数。
相对雷诺数定义为
Rep=ρdpupi-uiμ (11)
描述降雨环境特性的主要参数包括降雨强度、雨滴谱、雨滴降落末速度、体积分数等。通常情况下, 采用降雨强度来描述降雨的宏观特征量, 采用雨滴谱来描述降雨的微观特征量。Best根据现场观测数据建立雨滴谱(雨滴粒径的分布函数)计算公式[26]
{Η(dp)=1-exp[-(dpb1Ιb3)l]W=b2Ιb4 (12)
式中: H(dp)为总体积中直径不大于dp的雨滴所占百分数; I为降雨强度; W为单位体积空气中雨滴的总体积; b1、b2、b3、b4为经验系数, 取值分别为1.300、67.000、0.232、0.846;l为雨型常数, 取值为2.25。
在某一降雨强度下, 空气中的雨滴粒径分布是多种多样的, 但有一定的统计规律。根据Best的研究结果, 在某一固定降雨强度下, 选取雨滴数量最多的粒径值作为代表粒径, 其计算公式为[26]
dp=b1Ιb3(l-1l)1/l (13)
雨滴在降落时, 除了受自身重力外, 还受空气阻力作用。雨滴在下落的过程中, 雨滴降落速度不断增大, 空气阻力也随之增大, 直到与雨滴重力达到平衡。此后, 雨滴匀速下降, 此时雨滴的下落速度称为雨滴降落末速度。雨滴降落末速度与雨滴粒径有很大关系, 表示为[26-27]
v=9.58{1-exp[-(103dp1.77)1.147]} (14)
式中: v为雨滴降落末速度。
1.3 相间耦合
Euler-Lagrange方法一般有2种模拟途径: 一种是仅简单地考虑连续相对离散相颗粒的作用, 不考虑离散相颗粒对连续相的反作用, 即先求解流场, 然后将流动速度代入颗粒运动方程中计算颗粒的运动(非耦合方法), 该方法适用于离散相颗粒较为稀疏的情况; 另一种是考虑连续相和离散相颗粒之间的相互作用, 两者之间存在动量交换, 通过向流场动量方程中增加反映颗粒对流场影响的源项, 以此来计算颗粒和流场之间的动量传递(相间耦合方法), 该方法适用于相对较高的颗粒体积分数。Elghobashi根据离散相颗粒的体积分数指出, 当离散相体积分数低于10-6时, 颗粒运动对流场的影响很小, 可以采用非耦合方法; 当离散相体积分数为10-6~10-3时, 需要考虑离散相颗粒与流场的相互作用, 采用相间耦合方法[28]。本文中降雨强度模拟范围为100~500 mm·h-1, 对应的雨滴体积分数为3.3×10-6~1.3×10-5, 因此, 本文采用相间耦合方法进行降雨环境的模拟。连续相与离散相之间的动量交换主要是由相间阻力引起的, 根据雨滴的Lagrange运动方程, 相间动量交换可以表示为[8]
Μi=∑18μρpd2pcRep24(ui-upi)⋅mpΔt (15)
式中: ⋅mp为单位体积内的颗粒质量流率; Δt为作用时间。
2. 计算模型
借用某CRH型动车组的几何外形, 建立高速列车三维几何模型。由于转向架会对车底流场产生影响, 为更真实地反映降雨环境对高速列车空气动力学性能的影响, 本文的列车模型中考虑了转向架及风挡。考虑到多相流计算的复杂性及其对计算网格的极大需求, 本文中的高速列车采用1.5车编组, 此类模型在Railway Applications—Aerodynamics Part 6: Requirements and Test Procedures forCross Wind Assessment (BS EN 14067-6:2010)标准中被采用。计算区域如图 1所示, 其中车底与地面之间的距离为0.376 m, 计算区域左侧设置为速度入口边界条件, 右侧设置为压力出口边界条件, 两侧及顶端设置为对称边界条件, 底端设置为壁面边界条件。
本文模拟风洞吹风的方式来进行CFD计算, 即假设列车静止不动, 在列车前端计算区域入口设置来流风速, 来流风速大小等于车速, 来流风速方向与车速方向相反。对于降雨的模拟, 将计算区域顶端设置为入射面, 雨滴由计算区域顶端进入计算区域。在雨滴进入计算区域后, 受计算区域入口来流风速的影响, 雨滴在水平方向上产生速度, 且雨滴水平方向上的速度将达到计算区域入口来流风速[29], 因此, 由计算区域顶端入射的雨滴降落到地面上时, 将产生一定的水平运动距离。为保证雨滴能够完全降落到列车表面, 由计算区域最前端入射的雨滴在降落到地面上时, 应落到列车前方。从而在降雨环境下, 列车前方到计算区域入口的距离应足够长。本文计算的列车速度为200~400 km·h-1, 降雨强度为100~500 mm·h-1。考虑到列车速度400 km·h-1对应的区域前端来流风速最大, 此时雨滴具有最大的水平运动速度, 降雨强度100 mm·h-1对应的雨滴粒径最小, 此时雨滴具有最小的降落末速度, 在此2种组合情况下, 雨滴降落到地面时产生的水平运动距离最大, 经计算约为280 m, 从而列车前方到计算区域入口的距离至少应大于280 m。考虑到文中列车长度约38 m, 将列车后方到计算区域入口的距离设置为360 m(图 1), 可以保证由计算区域顶端入射的雨滴能够完全降落到列车表面。
网格划分时, 面网格采用三角形网格, 体网格采用四面体网格。车体表面网格尺寸设置为100 mm, 转向架和风挡表面网格尺寸设置为50 mm。列车表面设置边界层, 其首层厚度设置为1 mm, 增长比设置为1.2, 层数设置为6。图 2给出列车头部及转向架表面计算网格。
离散相雨滴的边界条件设置如下: 雨滴与车体表面的碰撞计算采用Stanton-Rutland模型; 计算区域入口及出口设置为逃逸边界, 即雨滴穿过计算区域而逃逸(雨滴的运动轨迹也在此处终止计算); 计算区域底端设为捕集边界, 即雨滴落在底端壁面后被捕集, 停止雨滴运动的模拟计算。
3. 计算模型验证
开展降雨环境下高速列车气动性能的试验验证是非常必要的, 通过与试验数据的对比, 有助于确定合理的数值计算参数, 保证数值计算的准确性和可靠性。然而强降雨下的高速列车气动性能试验开展难度大, 尚无相关工作发表。本文分别对高速列车空气动力学模型(无降雨)的准确性和雨滴模拟的可靠性进行验证。
3.1 空气动力学模型验证
为验证网格设置及空气动力学计算方法的准确性, 不考虑降雨, 开展高速列车空气动力学数值计算, 并将计算结果与既有风洞试验结果进行对比。数值计算时, 入口风速与风洞试验风速相同。图 3给出头车气动阻力系数CD的收敛曲线。通过取平均值可得, 头车气动阻力系数为0.152, 而风洞试验的头车阻力系数为0.145[30], 计算误差为4.83%, 可以满足工程计算精度要求。
3.2 多相流计算验证
雨滴在下落过程中受重力和空气阻力的作用, 最终是匀速下降的。选取粒径为0.5、1.0、1.5、2.0、2.5、3.0 mm的雨滴, 计算雨滴在重力和空气阻力作用下的运动轨迹, 获得不同粒径雨滴的降落末速度, 并通过与已有文献结果[25]的对比, 验证利用Euler-Lagrange方法进行降雨环境模拟的可靠性。
表 1给出不同粒径雨滴的降落末速度与文献[25]结果的比较。
表 1 雨滴降落末速度对比Table 1. Comparison of terminal velocities of raindrop雨滴粒径/mm 0.5 1.0 1.5 2.0 2.5 3.0 试验值/(m·s-1) 2.00 3.88 5.39 6.55 7.41 8.05 计算值/(m·s-1) 2.06 3.92 5.48 6.74 7.75 8.63 差值/(m·s-1) 0.06 0.04 0.09 0.19 0.34 0.58 由表 1可以看出: 随着雨滴粒径的增加, 计算值与试验值的差异有所增大, 当雨滴粒径为3.0 mm时, 计算值较试验值大0.58 m·s-1。这是因为数值计算时将雨滴假设为球形颗粒, 而实际观测表明, 当雨滴粒径较小时, 雨滴的形状近似为球形, 随着雨滴粒径的增大, 雨滴的形状逐渐变为纺锤形, 从而使计算误差增大。
综合而言, 利用Euler-Lagrange方法计算得到的不同粒径下的雨滴降落末速度与已有文献结果相差较小, 本文的多相流计算方法具有较好的准确性和可靠性。
4. 计算结果分析
数值计算时, 暂不考虑环境风的影响, 研究降雨强度及列车速度对高速列车气动性能的影响。降雨强度分别取0、100、200、300、400、500 mm·h-1, 列车速度分别取200、300、400 km·h-1。
图 4给出车速为300 km·h-1, 降雨环境下列车周围三维绕流流场中的雨滴颗粒分布。由图 4可知: 列车前方区域的雨滴已经降落到地面上, 整个列车车身都处于降雨区域内, 本文计算区域的选取是合适的; 雨滴颗粒在进入计算区域之后, 不仅受到自身的重力作用以一定的速度降落, 同时还受到计算区域入口风速的影响, 形成风驱雨现象, 雨滴会产生一定的水平速度, 雨滴水平速度略大于计算区域入口风速; 部分雨滴在与流线型头型碰撞后会破碎成小雨滴, 改变运行方向, 并随来流风速一起运动。
图 5给出车速为300 km·h-1时, 不同降雨强度下的流线型头型压力分布, 可以看出: 随着降雨强度的增加, 在雨滴的冲击作用下, 流线型头型前端区域的正压逐渐增大, 流线型头型后端区域的负压逐渐减小, 由此导致头车气动阻力增大。
图 6给出不同车速下的头车气动阻力系数和气动升力系数随降雨强度的变化规律, 可知: 降雨强度对气动阻力系数的影响较为明显, 而对气动升力系数的影响较小; 各个车速下气动阻力系数均随着降雨强度的增加而增大, 且与降雨强度近似呈线性关系; 无降雨时, 不同车速下的气动阻力系数和气动升力系数相差不大, 这是由于当雷诺数达到一定数值后, 气动力系数基本不再受车速影响; 在降雨环境下, 受雨滴冲击的影响, 不同降雨强度下的列车气动阻力增大, 进而导致列车气动阻力系数增大。
图 7给出气动阻力系数及气动阻力相对于无降雨工况的增加值随着车速及降雨强度的变化, 可知: 与无降雨时的气动阻力系数相比, 当降雨强度为100~500 mm·h-1时, 200 km·h-1车速下的气动阻力系数增加0.004 0~0.020 4, 气动阻力增加85~432 N, 增大率为2.64%~13.46%;300 km·h-1车速下的气动阻力系数增加0.002 7~0.013 7, 气动阻力增加129~652 N, 增大率为1.78%~9.05%;400 km·h-1车速下的气动阻力系数增加0.002 3~0.009 8, 气动阻力增加195~829 N, 增大率为1.52%~6.49%;在同一车速, 气动阻力系数和气动阻力的增大量随着降雨强度的增大而增大; 在同一降雨强度, 车速越高, 气动阻力相对于无降雨工况的增加值越大, 这是因为车速越高, 列车与雨滴的撞击作用越强; 对于气动阻力系数, 规律相反, 即车速越高, 气动阻力系数相对无降雨工况的增加值越小, 这主要是由于不同降雨强度下气动阻力的增加值近似与车速呈线性关系, 而气动阻力系数与车速平方成反比, 从而车速越高, 气动力阻力系数的增加值反而减小。
在实际的降雨过程中, 雨滴的粒径并不是单一的, 为此需要研究雨滴粒径的变化对高速列车气动阻力系数的影响。在列车速度300 km·h-1, 降雨强度100 mm·h-1条件下, 分析雨滴粒径对列车气动阻力系数的影响, 如图 8所示, 可知: 当车速为300 km·h-1, 降雨强度为100 mm·h-1, 雨滴粒径由2 mm增加为4 mm时, 气动阻力系数由0.152 0增大到0.154 9, 气动阻力增加138 N, 增大率为1.91%, 说明在相同的列车速度和降雨强度条件下, 高速列车气动阻力系数随着雨滴粒径的增加而增大, 且与雨滴粒径近似呈线性关系。
5. 结语
(1) 雨滴颗粒在进入计算区域之后, 不仅受到自身的重力作用以一定的速度降落, 同时还受到入口风速的影响, 形成风驱雨现象。
(2) 受雨滴的冲击作用, 流线型头型前端区域的正压逐渐增大, 流线型头型后端区域的负压逐渐减小, 由此将导致头车气动阻力增大。
(3) 在相同车速条件下, 降雨强度对气动阻力系数的影响较为显著, 而对气动升力系数的影响较小。气动阻力系数随着降雨强度的增加而增大, 且与降雨强度近似呈线性关系。
(4) 在同一降雨强度条件下, 车速越高, 气动阻力相对于无降雨工况的增加值越大, 而气动阻力系数相对于无降雨工况的增加值越小。
(5) 气动阻力系数随着雨滴粒径的增加而增大, 且与雨滴粒径近似呈线性关系。
(6) 本文针对降雨环境下的列车气动性能开展研究,没有考虑环境风的影响,实际中,降雨环境多伴有环境风。相对于单纯的降雨环境或强风环境,强风雨环境下的气流、雨滴与列车之间的相互作用更为复杂,高速列车的气动性能会进一步恶化。下一步将开展强风雨环境下高速列车空气动力学性能研究,分析降雨强度、车速、风速对高速列车气动性能的影响规律。此外,本文中的列车模型采用1.5车编组模型,无法考虑降雨环境对尾流的影响特征,下一步还需要建立更多编组情况下的列车模型,研究降雨环境对编组中不同车辆气动性能的影响规律。
-
表 1 参数
Table 1. Parameters
参数代号 参数含义 参数初始值 变化范围/% T1 轨道侧滚刚度/(N·m-1) 1.37×107 ±20 T2 转臂节点横向刚度/(N·m-1) 1.00×105 T3 轨道横向刚度/(N·m-1) 1.47×107 T4 一系弹簧横向刚度/(N·m-1) 9.80×105 T5 空气弹簧横向刚度/(N·m-1) 1.59×105 T6 转臂节点垂向刚度/(N·m-1) 6.60×105 T7 轨道垂向刚度/(N·m-1) 4.40×107 T8 一系弹簧垂向刚度/(N·m-1) 1.76×106 T9 轨道横向阻尼/[(N·s)·m-1] 6.50×106 T10 轨道垂向阻尼/[(N·s)·m-1] 4.00×104 T11 二系横向减振器阻尼/[(N·s)·m-1] 5.88×104 T12 一系垂向减振器阻尼/[(N·s)·m-1] 1.96×104 T13 二系垂向减振器阻尼/[(N·s)·m-1] 4.00×104 表 2 PCE模型拟合精度检验
Table 2. Fitting accuracy test of PCE model
检验序号 车轮垂向加速度/% 车轮垂向位移/% 车轮横向加速度/% 车轮横向位移/% 1 0.00 0.03 0.93 4.71 2 0.00 0.08 0.83 2.32 3 0.00 0.21 2.50 3.74 4 0.00 0.15 0.13 0.40 5 0.00 0.03 0.60 3.24 6 0.00 0.16 2.19 3.88 7 0.00 0.14 1.21 3.11 8 0.00 0.43 3.32 2.72 9 0.00 0.12 0.18 4.71 10 0.00 0.15 2.19 0.82 11 0.00 0.03 0.57 4.30 12 0.00 0.19 1.01 3.44 13 0.00 0.07 2.52 0.98 14 0.00 0.40 3.75 1.26 15 0.00 0.18 0.42 6.97 16 0.00 0.60 2.00 1.05 17 0.00 0.24 0.94 2.87 18 0.00 0.48 0.74 1.55 19 0.01 0.31 0.07 4.87 20 0.00 0.51 4.38 1.59 -
[1] 杨光, 任尊松, 孙守光. 考虑弹性的高速旋转轮对振动特性研究[J]. 振动工程学报, 2016, 29(4): 714-719. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201604019.htmYANG Guang, REN Zun-song, SUN Shou-guang. Research on the vibration characteristics of high-speed rotation elastic wheelset[J]. Journal of Vibration Engineering, 2016, 29(4): 714-719. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDGC201604019.htm [2] 李哲, 高军伟, 张柏娜. 基于RFID的列车轮对识别与振动监控系统设计[J]. 仪表技术与传感器, 2020(11): 64-67, 73. doi: 10.3969/j.issn.1002-1841.2020.11.014LI Zhe, GAO Jun-wei, ZHANG Bai-na. Design of train wheelset identification and vibration monitoring system based on RFID[J]. Instrument Technique and Sensor, 2020(11): 64-67, 73. (in Chinese) doi: 10.3969/j.issn.1002-1841.2020.11.014 [3] 庞学苗, 李建伟, 邢宗义, 等. 基于频率切片小波变换的轨道列车轮对振动信号分析[J]. 铁道机车车辆, 2015, 35(增刊1): 26-31. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJC2015S1008.htmPANG Xue-miao, LI Jian-wei, XING Zong-yi, et al. Analysis of wheel-rail vibration signal based on frequency sliced wavelet transform[J]. Railway Locomotive and Car, 2015, 35(Sup1): 26-31. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJC2015S1008.htm [4] 马卫华, 许自强, 罗世辉, 等. 轮轴弯曲刚度对轮轨垂向动态载荷影响分析[J]. 机械工程学报, 2012, 48(6): 96-101. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201206016.htmMA Wei-hua, XU Zi-qiang, LUO Shi-hui, et al. Influence of the wheel axle bending stiffness on the wheel/rail vertical dynamical load[J]. Chinese Journal of Mechanical Engineering, 2012, 48(6): 96-101. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201206016.htm [5] 张宝安. 柔性轮对结构振动对车辆动力学性能的影响[J]. 计算机辅助工程, 2013, 22(3): 19-23, 28. doi: 10.3969/j.issn.1006-0871.2013.03.004ZHANG Bao-an. Effect of structure vibration of flexible wheelset on vehicle dynamics performance[J]. Computer Aided Engineering, 2013, 22(3): 19-23, 28. (in Chinese) doi: 10.3969/j.issn.1006-0871.2013.03.004 [6] HAUG E J, WEHAGE R A, MANI N K. Design sensitivity analysis of large-scale constrained dynamic mechanical systems[J]. ASME Journal of Mechanisms, Transmissions, and Automation in Design, 1984, 106(2): 156-162. doi: 10.1115/1.3258573 [7] 余衍然, 李成, 姚林泉, 等. 基于傅里叶幅值检验扩展法的轨道车辆垂向模型全局灵敏度分析[J]. 振动与冲击, 2014, 33(6): 77-81. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201406014.htmYU Yan-ran, LI Cheng, YAO Lin-quan, et al. Global sensitivity analysis on vertical model of railway vehicle based on extended Fourier amplitude sensitivity test[J]. Journal of Vibration and Shock, 2014, 33(6): 77-81. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201406014.htm [8] 张旭明, 王德信. 结构灵敏度分析的解析方法[J]. 河海大学学报, 1998, 26(5): 47-52. https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX805.008.htmZHANG Xu-ming, WANG De-xin. Analytical method of structural sensitivity analysis[J]. Journal of Hohai University, 1998, 28(5): 47-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX805.008.htm [9] 聂祚兴, 于德介, 李蓉, 等. 基于Sobol'法的车身噪声传递函数全局灵敏度分析[J]. 中国机械工程, 2012, 23(14): 1753-1757. doi: 10.3969/j.issn.1004-132X.2012.14.027NIE Zuo-xing, YU De-jie, LI Rong, et al. Global sensitivity analysis of autobodies' noise transfer functions based on Sobol' method[J]. China Mechanical Engineering, 2012, 23(14): 1753-1757. (in Chinese) doi: 10.3969/j.issn.1004-132X.2012.14.027 [10] SOBOL I M, LEVITAN Y L. On the use of variance reducing multipliers in Monte Carlo computations of a global sensitivity index[J]. Computer Physics Communications, 1999, 117(1/2): 52-61. [11] SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271-280. [12] SOBOL I M. Theorems and examples on high dimensional model representation[J]. Reliability Engineering and System Safety, 2003, 79(2): 187-193. doi: 10.1016/S0951-8320(02)00229-6 [13] BIGONI D, TRUE H, ENGSIG-KARUP A P. Sensitivity analysis of the critical speed in railway vehicle dynamics[J]. Vehicle System Dynamics, 2014, 52(Sup1): 272-286. doi: 10.1080/00423114.2014.898776 [14] 邵永生, 李成, 成明. 基于Sobol'法的轨道车辆平稳性的全局灵敏度分析[J]. 铁道科学与工程学报, 2018, 15(3): 748-754. doi: 10.3969/j.issn.1672-7029.2018.03.027SHAO Yong-sheng, LI Cheng, CHENG Ming. Sensitivity analysis of rail vehicle front end energy absorption structure based on Sobol' method[J]. Journal of Railway Science and Engineering, 2018, 15(3): 748-754. (in Chinese) doi: 10.3969/j.issn.1672-7029.2018.03.027 [15] 陈秉智, 汪驹畅. 基于Sobol'法的轨道车辆前端吸能结构灵敏度分析[J]. 铁道学报, 2020, 42(3): 63-68. doi: 10.3969/j.issn.1001-8360.2020.03.008CHEN Bing-zhi, WANG Ju-chang. Global sensitivity analysis of energy-absorbing structure for rail vehicle based on Sobol' method[J]. Journal of the China Railway Society, 2020, 42(3): 63-68. (in Chinese) doi: 10.3969/j.issn.1001-8360.2020.03.008 [16] 张慧云. 基于径向基函数网络的高速列车参数设计与优化[D]. 成都: 西南交通大学, 2015.ZHANG Hui-yun. The high-speed train parameter design and optimazation based on radial basis function[D]. Chengdu: Southwest Jiaotong University, 2015. (in Chinese) [17] 周生通, 祁强, 周新建, 等. 轴弯曲与不平衡柔性转子共振稳态响应随机分析[J]. 计算力学学报, 2020, 37(1): 20-27. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202001004.htmZHOU Sheng-tong, QI Qiang, ZHOU Xin-jian, et al. Stochastic analysis of resonance steady-state response of rotor with shaft bending and unbalance faults[J]. Chinese Journal of Computational Mechanics, 2020, 37(1): 20-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG202001004.htm [18] 周生通, 张沛, 肖乾, 等. 单盘悬臂转子启动过程峰值响应全局灵敏度分析[J]. 振动与冲击, 2021, 40(11): 17-25. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202111004.htmZHOU Sheng-tong, ZHANG Pei, XIAO Qian, et al. Global sensitivity analysis for peak response of a cantilevered rotor with single disc during start-up[J]. Journal of Vibration and Shock, 2021, 40(11): 17-25. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202111004.htm [19] 周生通, 王迪, 肖乾, 等. 基于广义多项式混沌的跨座式单轨车辆随机平稳性分析[J]. 振动与冲击, 2021, 40(6): 190-200. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202106026.htmZHOU Sheng-tong, WANG Di, XIAO Qian, et al. Stochastic stationarity analysis of a straddle monorail vehicle using the generalized polynomial chaos method[J]. Journal of Vibration and Shock, 2021, 40(6): 190-200. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202106026.htm [20] FORMAGGIA L, GUADAGNINI A, IMPERIALI I, et al. Global sensitivity analysis through polynomial chaos expansion of a basin-scale geochemical compaction model[J]. Computational Geosciences, 2013, 17(1): 25-42. doi: 10.1007/s10596-012-9311-5 [21] SUDRET B. Global sensitivity analysis using polynomial chaos expansions[J]. Reliability Engineering and System Safety, 2008, 93(7): 964-979. doi: 10.1016/j.ress.2007.04.002 [22] GARCIA-CABREJO O, VALOCCHI A. Global sensitivity analysis for multivariate output using polynomial chaos expansion[J]. Reliability Engineering and System Safety, 2014, 126: 25-36. doi: 10.1016/j.ress.2014.01.005 [23] 黄悦琛, 宋长青, 郭荣化. 基于广义多项式混沌展开的无人机飞行性能不确定性分析[J]. 飞行力学, 2021, 39(4): 25-32, 51. https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX202104005.htmHUANG Yue-chen, SONG Chang-qing, GUO Rong-hua. Uncertainty analysis of unmanned aerial vehicle flight performance using general polynomial chaos expansion[J]. Flight Dynamics, 2021, 39(4): 25-32, 51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FHLX202104005.htm [24] 王晗, 严正, 徐潇源, 等. 基于稀疏多项式混沌展开的孤岛微电网全局灵敏度分析[J]. 电力系统自动化, 2019, 43(10): 44-52. doi: 10.7500/AEPS20180625006WANG Han, YAN Zheng, XU Xiao-yuan, et al. Global sensitivity analysisfor islanded microgrid based on sparse polynomial chaos expansion[J]. Automation of Electric Power Systems, 2019, 43(10): 44-52. (in Chinese) doi: 10.7500/AEPS20180625006 [25] 刘安民, 高峰, 张青斌, 等. 基于多项式混沌展开方法的翼伞飞行不确定性[J]. 兵工学报, 2021, 42(7): 1392-1399. doi: 10.3969/j.issn.1000-1093.2021.07.006LIU An-min, GAO Feng, ZHANG Qing-bin, et al. Application of PCE method in parafoil-flight uncertainty analysis[J]. Acta Armamentarii, 2021, 42(7): 1392-1399. (in Chinese) doi: 10.3969/j.issn.1000-1093.2021.07.006 [26] WIENER N, The homogeneous chaos[J]. American Journal of Mathematics, 1938, 60(4): 897. doi: 10.2307/2371268 [27] GHANEM R, GHOSH D. Efficient characterization of the random eigenvalue problem in a polynomial chaos decomposition[J]. International Journal For Numerical Methods in Engineering. 2007, 72(4): 486-504. doi: 10.1002/nme.2025 [28] 胡军, 张树道. 基于多项式混沌的全局敏感度分析[J]. 计算物理, 2016, 33(1): 1-14. doi: 10.3969/j.issn.1001-246X.2016.01.001HU Jun, ZHANG Shu-dao. Global sensitivity analysis based on polynomial chaos[J]. Chinese Journal of Computational Physics, 2016, 33(1): 1-14. (in Chinese) doi: 10.3969/j.issn.1001-246X.2016.01.001 [29] 赵威, 卜令泽, 王伟. 稀疏偏最小二乘回归-多项式混沌展开代理模型方法[J]. 工程力学, 2018, 35(9): 44-53. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201809007.htmZHAO Wei, BU Ling-ze, WANG Wei. Sparse partial least squares regression-polynomial chaos expansion metamodeling method[J]. Engineering Mechanics, 2018, 35(9): 44-53. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201809007.htm [30] 周如意, 丰文浩, 邓宗全, 等. 轮地力学模型参数灵敏度分析与主参数估计[J]. 航空学报, 2021, 42(1): 524076. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202101020.htmZHOU Ru-yi, FENG Wen-hao, DENG Zong-quan, et al. Sensitivity analysis and dominant parameter estimation of wheel-terrain interaction model[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(3): 524076. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202101020.htm [31] 付娜, 李成辉, 赵振航, 等. 车辆-轨道耦合作用下桥上减振双块式无砟轨道减振性能研究[J]. 铁道科学与工程学报, 2018, 15(5): 1095-1102. doi: 10.3969/j.issn.1672-7029.2018.05.001FU Na, LI Cheng-hui, ZHAO Zhen-hang, et al. Study on the vibration reduction performance of double-block ballastless damping track on bridge under vehicle-track coupling effect[J]. Journal of Railway Science and Engineering, 2018, 15(5): 1095-1102. (in Chinese) doi: 10.3969/j.issn.1672-7029.2018.05.001 期刊类型引用(8)
1. 许建民,杨炜,龚晓岩,武颂,李洛楠. 风雨耦合环境下驾驶队列的气动特性研究. 汽车安全与节能学报. 2024(04): 492-502 .  百度学术
百度学术2. 胡春雨,于梦阁,盛旭高,李美香. 风雨环境下汽车空气动力学性能分析. 青岛大学学报(工程技术版). 2023(01): 77-84 .  百度学术
百度学术3. 李中奇,唐博伟,杨辉,黄琳静. 高速动车组分布式全局快速终端滑模控制策略. 铁道学报. 2023(04): 41-50 .  百度学术
百度学术4. 盛旭高,于梦阁,刘加利. 基于M-P雨滴谱的强降雨环境下高速列车雨载荷及气动特性分析. 空气动力学学报. 2022(02): 122-128 .  百度学术
百度学术5. 唐兆,董少迪,罗仁,蒋涛,邓锐,张建军. 人工智能算法在铁道车辆动力学仿真中的应用进展. 交通运输工程学报. 2021(01): 250-266 .  本站查看
本站查看6. 朱海燕,曾庆涛,王宇豪,曾京,邬平波,朱志和,王超文,袁遥,肖乾. 高速列车动力学性能研究进展. 交通运输工程学报. 2021(03): 57-92 .  本站查看
本站查看7. 彭益华,何旭辉,敬海泉,谢能超. 风雨耦合作用下高速列车气动性能的风洞试验研究. 中南大学学报(自然科学版). 2021(09): 3353-3365 .  百度学术
百度学术8. 文恒,于梦阁,盛旭高,殷硕. 沙尘环境下高速列车气动特性分析. 青岛大学学报(工程技术版). 2020(04): 50-54+76 .  百度学术
百度学术其他类型引用(6)
-






 下载:
下载:








 下载:
下载:














 百度学术
百度学术








