Global bilevel polynomial optimization model for continuous traffic network design
-
摘要: 提出了一种面向典型连续交通网络设计问题的全局双层多项式优化模型,其函数均为多项式,且下层问题为凸问题;上层问题旨在优化网络性能,下层问题用来刻画确定性用户均衡(DUE)交通流模式;利用Fritz John条件和乘子代替下层规划,将提出的双层多项式优化模型转换为等价单层优化问题,并利用矩半定规划(MSDP)方法得到其全局最优解;利用矩矩阵的秩作为保证全局最优性的充分条件,并估计全局最优解的个数;给出了最优道路收费问题的数值算例,用提出的双层多项式优化模型描述了算例中的最优道路收费问题,并通过Wardrop用户均衡约束调整现有路段上的交通流量,使总通行费收益最大化。研究结果表明:该简单算例的最大收益为13.5元,同时可以得到该算例的矩矩阵的秩为1,从而证明了该结果的全局最优性,提出的方法克服了均衡约束数学规划(MPEC)法和值函数法等现有求解双层优化问题的经典算法由于连续交通网络设计固有的非凸性,只能找到局部最优的问题;提出的全局双层多项式优化模型与算法为典型连续交通网络设计提供了更好的探索工具。Abstract: A global bilevel polynomial optimization model for a typical continuous traffic network design problem was proposed. In this model, all the functions are polynomials, and the lower-level problem is a convex problem. The upper-level problem is to optimize the network performance, and the lower-level problem is to characterize the traffic flow pattern of the deterministic user equilibrium (DUE). The bilevel polynomial optimization model was transformed into an equivalent single-level optimization problem by replacing the lower-level programming with the Fritz John conditions and multipliers, and then the moment semi-definite programming (MSDP) method was employed to obtain its global optimal solutions. The ranks of moment matrices were taken as sufficient conditions to guarantee the global optimality and were used to estimate the number of global optimal solutions. Moreover, a numerical example for the optimal toll problem was given, and the optimal toll problem was depicted by the proposed bilevel polynomial optimization model. The total toll revenue was maximized by adjusting the traffic flow on the existing road sections under the Wardrop user equilibrium constraint. Research results reveal that the maximum revenue in this simple example is 13.5 yuan, and meanwhile, the rank of the moment matrix for the example is 1, which proves the global optimality of the results. The classical approaches to solving the bilevel optimization problem, such as the mathematical program with equilibrium constraints (MPEC) and value function methods, can only find local optimal solutions due to the inherent nonconvexity in the continuous traffic network design. However, the proposed approach overcomes the problem existing in classical algorithms, and the proposed global bilevel polynomial optimization model and algorithm provide a better exploration tool for a typical continuous traffic network design. 2 figs, 37 refs.
-
0. 引言
交通拥挤、交通安全、交通环境等交通问题已经成为城市居民日常关心的重大问题之一。交通网络设计是改善出行质量、缓解上述交通问题的基本手段之一。粗略地说,交通网络设计问题(Transportation Network Design Problem, TNDP)是指在有限的可用资源约束下设计目标网络,优化交通网络性能,使其以最佳状态服务于目标。TNDP[1]大致分为道路网络设计问题(Road Network Design Problem, RNDP)和公交网络设计问题(Public Transportation Network Design Problem, PTNDP)2类。RNDP又可分为连续网络设计问题(Continuous Network Design Problem, CNDP)、离散网络设计问题(Discrete Network Design Problem, DNDP)与混合网络设计问题(Mixed Network Design Problem, MNDP)3类。由于交通网络设计问题的内在复杂性,全局最优的一般交通网络设计问题没能得到很好解决,故其一直是开放的问题。交通网络设计具有基础重要性,因此,其在最近50年中一直是交通工程研究中的热点问题。
Farahani等[1-7]分别综述了交通网络设计问题的研究成果。由这些综述可知,交通网络设计中的一大类问题可表述为具有上下2层结构的Stackelberg博弈问题或领导者-跟随者问题。上层问题是领导者、设计者或规划、管理运输网络的决策者的问题,包括设定可衡量的目标(如减少总旅行时间、增加税收)、约束(如实际运行环境限制)和决策变量(如要修建的新道路和收费额度),其假设领导者可以预测跟随者的行为;下层问题是决定出行的跟随者问题,常用来描述出行方式和路线。双层结构使决策者可以考虑出行者的反应,并改善网络以影响出行者的选择,但不能直接控制他们的选择。出行者不被允许预测领导者的决定,而仅允许他们在知道领导者的决定之后确定他们的选择。从数学上讲,双层优化方法特别适合用来描述这种结构的问题。上层问题目标函数是要在一定的约束条件下最大化或最小化特定指标的目标函数,如系统总出行时间最小[8-9]、总建造成本最小[10]、网络备用能力最大[11-12]、用户盈余最大[13]、网络中的OD需求最大[14-15]等;下层问题常采用优化或变分不等式描述的均衡模型。组合不同的上层问题与不同的下层出行选择行为模型,就可以得到多种不同的网络设计双层优化模型。通常,双层优化问题被认为很难解决。本文面向交通网络设计问题,研究一类基于连续变量、全部函数为多项式的全局最优双层优化模型及其算法实现。
交通网络设计问题中最具代表性、引领性的研究问题包括OD矩阵估计、网络容量扩充设计、道路收费、信号灯优化设计以及它们的组合问题等。双层优化是一类困难的优化问题。即使上下层所有函数都是线性的,双层优化问题仍然是非确定性多项式难的[16];即使上下层问题都是凸规划,双层优化问题仍然可能是非凸的[17]。由于双层优化问题内在的复杂性,使得求解算法的多样性受到极大限制[18-19]。目前已知的求解算法可分为精确算法和启发式算法2类。求解离散网络设计问题常用方法有Bender分解法、分支定界法和启发式算法(遗传算法、粒子群算法等)。混合网络设计问题主要采用元启发式方法来解决,传统分析类型的数值求解算法不多。已有文献中关于CNDP的研究最多。CNDP属于交通网络设计中的经典研究问题。学者们针对CNDP设计了许多算法,其中大部分是启发式算法。求解CNDP的启发式算法粗略地可以分为3类[20]:迭代优化分配(Iterative-Optimization-Assignment, IOA)算法、路段使用比例(Link Usage Proportion-Based, LUPB)算法和灵敏度分析(Sensitivity Analysis-Based, SAB)算法。一些算法的应用需要强的假设条件,否则全局或局部收敛性无法得到保证,因而其具有很大的局限性。在采用经典算法的交通网络设计研究中,其解决双层优化的一般思路是将原双层优化问题转换为单层优化问题,然后求解该单层模型。Abdulaal等[21]将他们的问题重新表述为无约束优化,并用Hooke-Jeeves直接搜索方法求解;Marcotte[22]将一定限制条件下的CNDP转化为一个单层等价可微优化问题,并用约束累加算法求解;Davis[23]将CNDP转化为单层问题,并使用序列二次规划和广义简约梯度法求解。以上3篇代表性文献均未对其解的性质作深入讨论。对于连续变量的双层优化问题,过去25年最具有代表性的方法是均衡约束数学规划(Mathematical Program with Equilibrium Constraints, MPEC)与值函数方法。均衡约束数学规划指的是用下层规划的Kurash-Kuhn-Tucker(KKT)条件替换下层模型。这种方法的缺陷是,如果下层规划问题是非凸的,双层优化问题的最优解甚至可能不是MPEC单层优化问题的稳定点[24],即使下层规划问题是凸的,用KKT条件替换下层规划得到的MPEC的局部解可能不是原始双层优化的局部解[25]。解决双层优化的另一种方法是使用值函数将原问题重构为新模型[26]或者将MPEC与值函数组合在一起使用[27]。Meng等[28]使用边际函数表示确定性用户均衡(Deterministic User Equilibrium, DUE)条件,开发了增广拉格朗日方法来求解重构的问题,从而获得了局部最优解;Gao等[9]在强假设条件下利用值函数工具和上下层目标函数(上层目标函数为系统最优,下层目标函数为用户平衡)之间的特定关系将所研究的双层优化模型转化为单层凸规划模型,然后采用相应凸规划算法得到双层优化问题的全局最优解。由于模型结构特殊且假设条件很强,使得该方法难以被推广到一般问题的求解。有必要指出的是,很多情况下双层优化的最优解可能不是采用值函数方法重构的单层优化模型的稳定点,这使得值函数方法也有相当大的局限性[27]。除了上述方法外,还有学者使用分支定界法、下降法和罚函数法求解双层优化问题。Wang等[10]将特殊的CNDP转换为混合整数线性规划,并使用CPLEX求解,得到混合整数线性规划的全局最优解,但未在一般条件下证明用KKT条件替换下层规划得到的MPEC与原双层优化的等价性,因而其研究结论有待进一步深化。已有研究中介绍的精确算法绝大多数得到的是收敛点、稳定点或局部最优解。一般来说,经转换得到的单层优化问题通常都是非凸优化问题。由于非凸优化问题的内在复杂性,使得求解算法的选择与解的性质的讨论受到很大限制。事实上很多情况下很难找到非凸优化问题的全局最优解。例如,Li等[29]在很强的假设条件下证明用凸差(Difference of Convex, DC)算法转换后得到的单层模型的等价性,但未在一般条件下证明所设计的序列方法一定能得到子问题的全局最优解,因而其研究结论值得进一步探讨。概而言之,交通研究领域里采用的这些方法在识别局部解时都或多或少地有效,但不能保证全局最优解。精确求解CNDP的主要困难在于即使得到了最优解,由于其固有的非凸性,也无法确定该解是否是全局最优解。
迄今为止,连续变量的交通网络设计问题的研究成果是最多的,尤其是研究带有确定性用户均衡约束的交通网络设计(Transportation Network Design with Determicnistic User Equilibrium Constraints, TND-DUEC)问题的建模和算法的成果较多。已有TND-DUEC类模型基本采用启发式或局部精确解算法,对于典型问题仍然缺乏一般条件下的全局收敛方法。针对此问题,本文以所有函数都可以用非负多项式刻画的TND-DUEC双层优化模型为研究对象,应用Fritz John条件将该双层多项式优化模型简化为一个等价的单层多项式优化模型,并将其进一步转化为一个等价的矩半定规划(Moment Semi-Definite Programming, MSDP)模型,其解具有全局最优的理想属性;将本文方法用于一类典型道路收费问题,从理论上给出了双层优化模型刻画的带有确定性用户均衡约束的道路收费问题的全局最优解。
1. 双层多项式优化模型
1.1 符号与假设
考虑网络G=(N, A),其中:N为节点集;A为有向路段集。对于A中的路段a,有一个与之相对应的阻抗函数ta(ηa),其中ηa为路段a的交通量。令W为OD对集合;Rw为连接OD对w(w∈W)的所有可行路径的集合;hr, w为连接OD对w的路径r(r∈Rw)上的交通量;Dw为连接OD对w的交通需求;δa, r, w为路段a与路径r和w的拓扑关系,如果路径r使用路段a连接OD对w,δa, r, w=1,否则δa, r, w=0;Rn为n维实数空间;R+n为n维非负实数空间。对整个交通网络做以下假设:网络是强连通的;路段阻抗函数是关于路段流量的连续可微的严格增函数,且是连续可导的实系数非负多项式函数。
TND-DUEC问题是在考虑网络确定性用户均衡选择行为的基础上确定一组决策变量,使某个交通网络设计目标达到最优的一类决策问题。这类问题可以表述为双层优化问题。为便于讨论,对待建模型作如下假设。
(1) 双层优化问题的目标函数和上、下层问题的约束函数都是多项式。
(2) 下层规划是确定性用户均衡(凸规划)的。
(3) 下层规划问题的可行集独立于上层规划问题的决策变量。
(4) 双层优化问题可行集非空。
(5) 待研究双层优化属于乐观双层优化,即领导者在和跟随者的博弈中假定跟随者是合作的,领导者可以选择最优的决策方案。
1.2 TND-DUEC模型
基于上述假设,可将TND-DUEC问题构建为如下非线性双层优化问题
{minξZ=p(ξ,η)s.t.Fi1(ξ,η)≤0i1=1,2,⋯,q1Hj1(ξ,η)=0j1=1,2,⋯,q2minηz=∑a∈A∫ηa0ta(ω,ξ)dωs.t.∑r∈Rwhr,w=Dwηa=∑w∑rhr,wδa,r,wηa≥0 (1) 式中:p(ξ, η)为上层目标函数;Z为上层目标函数值;ξ=(ξ1, ξ2, …, ξn1)T,为上层决策变量向量,n1为其维数;η =(η1, η2, …, ηn2)T,为下层严格凸规划问题的最优解向量,n2为其维数;Fi1(ξ, η)为第i1个上层不等式约束函数;q1为不等式约束个数;Hj1(ξ, η)为第j1个上层等式约束函数;q2为等式约束个数;ta(·)为与路段a对应的阻抗函数,为非负严格增函数;ω为积分变量;z为下层目标函数值。
任意优化问题中所有的等式约束都可以写为不等式约束。为了研究TND-DUEC问题且不失一般性,将式(1)转化为如下仅包含不等式约束的连续交通网络设计双层优化统一模型
{minξ∈Rn1η∈Rn2Z=p(ξ,η)s.t.θi(ξ,η)≤0i=1,2,⋯,m1η∈Ψ(ξ):=argminζ∈Rn2{φ(ξ,ζ):ϕj(ζ)≤0j=1,2,⋯,m2} (2) 式中:θi(ξ, η)为第i个上层规划问题的约束条件;m1为上层不等式约束个数;φ(ξ, ζ)为下层规划目标函数;ϕj(·)为第j个下层规划问题的约束条件;ζ为下层决策变量;m2为下层不等式约束个数。
2. 模型求解与算法
2.1 等价的单层优化模型
一般的非线性双层优化问题的反应函数内在的非凸性和不可分性使其很难求解,特别是求得全局最优解更为困难。采用MPEC单层方法或值函数工具将双层优化模型转化为单层优化问题是应用广泛的思路。本文与之不同,基于如下定理,即应用Fritz John条件与乘子将式(2)转化为一个等价的单层优化模型。
定理1[30] 对于式(1),若下层问题满足非退化和Slater条件,则(ξ, η)∈Rn1×Rn2为式(1)的全局最优解,当且仅当存在拉格朗日乘子λ =(λ0, λ1, …, λm2)T时,(ξ, η, λ)∈Rn1×Rn2×Rm2+1是如下单层多项式优化模型的全局最优解
{minξ∈Rn1η∈Rn2λ∈Rm2+1Z=p(ξ,η)s.t.θi(ξ,η)≤0λ0∇ηφ(ξ,η)+m2∑j=1λj∇ηφj(η)=0λ0≥0m2∑j=0λ2j=1λjϕj(η)=0λj≥0ϕj(η)≤0 (3) 式中:▽ηφ(ξ, η)为关于η求梯度。
上述定理的要点在于使用Fritz John条件和拉格朗日乘子取代下层规划,把式(1)等价转化为式(3)。式(3)的计算仍然是非确定性多项式难的。解决式(3)的典型方法有代数方法和凸松弛方法,其中非负的多项式平方和(Sum Of Squares, SOS)松弛[31]与Lasserre提出的层次半定规划(Semidefinite Programming, SDP)松弛方法[32]是最常用的2种方法。本文沿用Lasserre提出的思路求解式(3)。为此,首先介绍实代数理论中的一些概念。
设x =(ξ, η, λ),且x=(x1, x2, …, xn),n=n1+n2+m2+1。令R[x]为由x构成的所有实多项式的环。复杂的多项式可表为若干单项式的线性组合。本文采用符号xα表示一个单项式,α=(α1, α2, …, αn)T∈ Nn(Nn为包含0在内的自然数集),为复合序号,|α|为xα的阶次,则任意一个单项式可以定义为
xα:=xα11xα22xα33⋯xαn (4) |{\bf{ \pmb{\mathit{ α}} |:}} = \sum\limits_{{i_2} = 1}^n {{\alpha _{{i_2}}}} (5) 式中:αi2为单项式中第i2(i2=1, 2, …, n)个变量的指数。
定义d阶扩展向量vd(x)为
\begin{array}{l} {\mathit{\boldsymbol{v}}_d}(\mathit{\boldsymbol{x}}): = \left( {1, {x_1}, \cdots , {x_n}, x_1^2, {x_1}{x_2}, \cdots , {x_1}{x_n}, x_2^2, } \right.\\ {\left. {\;\;\;\;\;\;\;{x_2}{x_3}, \cdots , x_n^2, \cdots , x_1^d, \cdots , x_n^d} \right)^{\rm{T}}} \end{array} (6) 若确定了式(6)所示的d阶扩展向量vd(x),任意d阶多项式函数f(x)可表示为xα的线性组合
f(\mathit{\boldsymbol{x}}) = \sum\limits_\mathit{\boldsymbol{\alpha }} {{f_\mathit{\boldsymbol{\alpha }}}} {\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{\alpha }}} (7) 式中:fα为单项式xα的系数。
可以将d阶多项式函数写成更高阶的表达形式,其中高于阶次d的单项式系数设为0。
将式(3)中所有约束改为等价的不等式约束,设共有m个,即转换之后的约束设为gi(x)≥0,i=1, 2, …, m,则由式(3)约束构成的可行解集合为半代数集K
K = \left\{ {\mathit{\boldsymbol{x}} \in {\mathbb{R} ^n}\mid {g_i}(\mathit{\boldsymbol{x}}) \ge 0, {g_i}(\mathit{\boldsymbol{x}}) \in \mathit{\boldsymbol{R}}[x]} \right\} (8) 基于式(8),将式(3)转化为式(9),即给定一个基本闭半代数集K,多项式优化的目的就是找到目标函数p(x)(p(x)∈ R[x])的全局最小值p*,即
{p^ * } = \inf \{ p(\mathit{\boldsymbol{x}})\mid \mathit{\boldsymbol{x}} \in K\} (9) 式中:inf{·}为下确界。
其对应的最优解x*为
{x^ * } = \left\{ {\mathit{\boldsymbol{x}}\mid \mathit{\boldsymbol{x}} \in K, p\left( {{\mathit{\boldsymbol{x}}^ * }} \right) \le p(\mathit{\boldsymbol{x}})} \right\} (10) 借用上述关于多项式的符号表示,将式(9)表示为如下的多项式优化问题
\left\{ {\begin{array}{*{20}{l}} {\min p(\mathit{\boldsymbol{x}}) = \sum\limits_\mathit{\boldsymbol{\alpha }} {{p_\mathit{\boldsymbol{\alpha }}}} {\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{\alpha }}}}\\ {{\rm{ s}}{\rm{.t}}{\rm{.}}{g_i}(\mathit{\boldsymbol{x}}) = \sum\limits_\mathit{\boldsymbol{\alpha }} {{g_{i\mathit{\boldsymbol{\alpha }}}}} {\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{\alpha }}} \ge 0} \end{array}} \right. (11) 式中:pα为p(x)中每个单项式xα的系数;giα为第i个约束的多项式函数gi(x)中每个单项式xα的系数。
矩可以表示为概率测度μ(μ∈ \mathcal{M} (K))下的积分[33]。Lasserre提出的求解式(11)的基本思想是采用矩半定规划松弛,其用\mathbb{R} n上无穷维测度意义下的等价凸优化问题式(12)来代替式(11),即
{p^ * } = \min \left( {\mathop \smallint \nolimits^ p(\mathit{\boldsymbol{x}})\mu {\rm{d}}\mathit{\boldsymbol{x}}\mid \mu \in {\mathcal{M}}(K)} \right) (12) 式(11)定义了K上的概率测度集\mathcal{M}(K),概率测度μ满足通常的概率性质μ (\emptyset )=0,μ(K)=1。可以基于μ定义α阶矩。令yα为单项式xα对应于概率测度μ的矩,则得矩序列y={yα},其中
{y_\mathit{\boldsymbol{\alpha }}} = \int\limits_K {{\mathit{\boldsymbol{x}}^\alpha }{\rm{d}}\mu (\mathit{\boldsymbol{x}})} (13) 多项式函数f(x)的矩L[f(x)]可以表示为
L[f(\mathit{\boldsymbol{x}})] = \int f (\mathit{\boldsymbol{x}}){\rm{d}}\mu (\mathit{\boldsymbol{x}}) (14) 将式(7)代入函数的矩表达式(14)并结合式(13)可得
L[f(\mathit{\boldsymbol{x}})] = \int {\left( {\sum\limits_\mathit{\boldsymbol{\alpha }} {{f_\mathit{\boldsymbol{\alpha }}}} {x^\mathit{\boldsymbol{\alpha }}}} \right)} {\rm{d}}\mu (\mathit{\boldsymbol{x}}) = \sum\limits_\mathit{\boldsymbol{\alpha }} {{f_\mathit{\boldsymbol{\alpha }}}} {y_\mathit{\boldsymbol{\alpha }}} (15) MSDP松弛方法的思路是,将式(11)中的多项式目标函数与约束函数分别转化为关于矩变量的线性关系式的目标函数和关于矩变量的半正定矩阵约束,从而对式(11)建立等价的凸半定规划松弛模型。
MSDP松弛方法的关键是给出矩变量的矩矩阵和局部化矩阵的计算表达式。
定义对应的s阶矩矩阵Ms(y)为
{\mathit{\boldsymbol{M}}_s}(y) = L\left[ {{\mathit{\boldsymbol{v}}_s}(\mathit{\boldsymbol{x}}){\mathit{\boldsymbol{v}}_s}{{(\mathit{\boldsymbol{x}})}^{\rm{T}}}} \right] (16) 式中:L(·)为式(14)所定义的矩;vs(x)为s阶扩展向量。
s阶矩矩阵Ms(y)中的元素记作Ms(y) β, γ,且
{\mathit{\boldsymbol{M}}_s}{(y)_{\mathit{\boldsymbol{\beta , \gamma }}}} = L\left( {{\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{\beta }}}{\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{\gamma }}}} \right) = {y_{\mathit{\boldsymbol{\beta + \gamma }}}} (17) 式中:β, γ ∈\mathbb{N} n,为矩阵的行序号和列序号,且|β|, |γ|≤s。
定理2 矩矩阵Ms(y)由所有矩变量yα组成,在矩变量空间,由矩变量构成的矩阵Ms(y)为半正定矩阵[32],即
{\mathit{\boldsymbol{M}}_s}(y) \ge 0 (18) 给定不等式约束的多项式函数g(x),用部分矩变量yα(|α|≤2s)定义与多项式函数g(x)相关的局部化矩矩阵Ms′[g(x)y]为
{\mathit{\boldsymbol{M}}_{s'}}[g(\mathit{\boldsymbol{x}})y] = L[g(\mathit{\boldsymbol{x}})]{\mathit{\boldsymbol{M}}_{s'}}(y) (19) L[g(\mathit{\boldsymbol{x}})] = \sum\limits_\mathit{\boldsymbol{\alpha }} {{g_\mathit{\boldsymbol{\alpha }}}} {y_\mathit{\boldsymbol{\alpha }}} (20) {\mathit{\boldsymbol{M}}_{s'}}(y) = L\left[ {{\mathit{\boldsymbol{v}}_{s'}}(\mathit{\boldsymbol{x}}){\mathit{\boldsymbol{v}}_{s'}}{{(\mathit{\boldsymbol{x}})}^{\rm{T}}}} \right] (21) 式中:L[g(x)]为多项式函数g(x)的矩;Ms′(y)为s′阶矩矩阵,且s′ < s;gα为函数g(x)中每个单项式xα的系数。
定理3 约束g(x)≥0的等价关系是矩阵Ms′[g(x)y]正半定[32],即
g(\mathit{\boldsymbol{x}}) \ge 0 \Leftrightarrow {\mathit{\boldsymbol{M}}_{s'}}[g(\mathit{\boldsymbol{x}})y] \ge 0 (22) 指定0阶次矩为1,即y0, …, 0=1。根据式(14)、(18)和(22),可得式(11) 的等价SDP松弛为
\left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_y \;\;L[p(\mathit{\boldsymbol{x}})] = \sum\limits_\mathit{\boldsymbol{\alpha }} {{p_\mathit{\boldsymbol{\alpha }}}} {y_\mathit{\boldsymbol{\alpha }}}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;{y_{0, \cdots , 0}} = 1}\\ {\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}_s}(y) \ge 0}\\ {\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}_{s'}}\left[ {{g_i}(\mathit{\boldsymbol{x}})y} \right] \ge 0\;\;\;\;\;i = 1, 2, \cdots , m} \end{array}} \right. (23) 式中:L[p(x)]为p(x)的矩。
2.2 模型的算法
式(23)为标准的SDP问题,调用SDP计算软件包,如SeDuMi[34]、SDPT3[35]等可求得式(23)中的各个矩变量的解,也可取适当的对称矩阵,写出式(23)中的对偶模型,从对偶问题的角度求解式(23)。
s可取1、2、…,甚至很大的值,而变量的数量会随着s的增加呈指数增长。已有研究[31]证明:当s增加时,相对较小的s就可以达到全局最小值,即相对较小的s可以使得式(23)的最优值逼近原问题的全局最小值。
判断求解式(23)得到矩变量的解是全局最优解的充分条件如下。
定理4[36] 设y*为式(23)的最优矩解,当矩矩阵的秩满足如下条件时,则式(23)的目标函数值与原问题式(11)的全局最优值p*相等,即
{\rm{rank}}\left[ {{\mathit{\boldsymbol{M}}_s}\left( {{y^ * }} \right)} \right] = {\rm{rank}}\left[ {{\mathit{\boldsymbol{M}}_{s - 1}}\left( {{y^ * }} \right)} \right] = \kappa (24) 式中:rank(·)为对矩阵取秩;秩κ表示原问题具有κ个全局最优解。
求得式(23)的全局最优矩解,接下来的工作是矩还原问题,也就是由矩解还原得到式(11)的解。这包括两方面:若矩矩阵的秩为1,对应原问题的全局最优解x*是唯一的,根据矩矩阵的结构特点,x*可从M1(y*)的第1行(第1列)直接得到。若矩矩阵的秩为κ且κ大于1,则原问题有κ个全局最优解。此时采用三阶段方法求解[36]:矩矩阵的奇异值分解、构造提取等式、采用特征值法求解精确最优解。
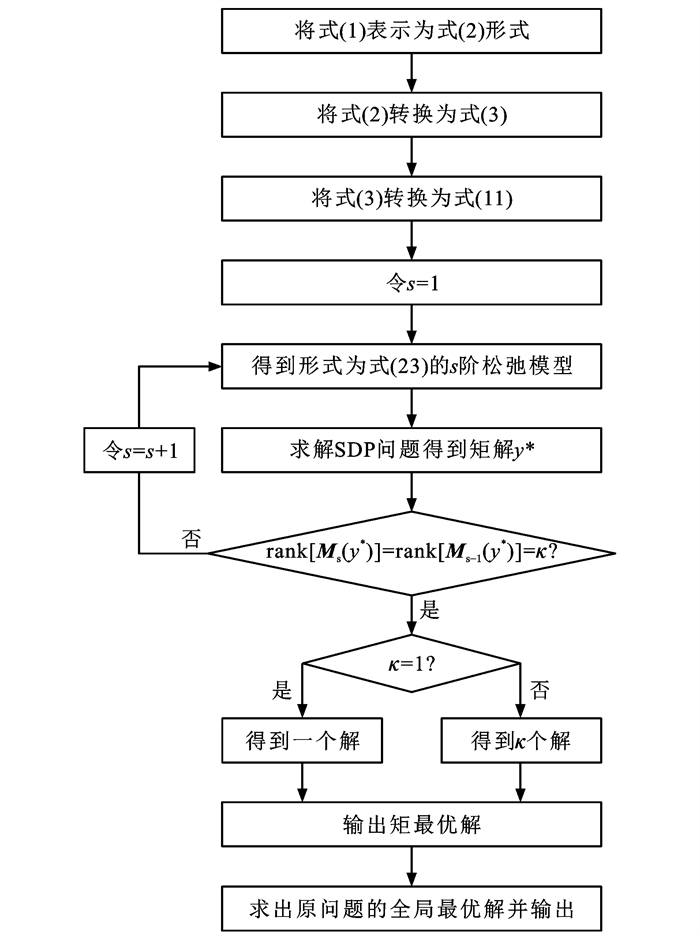
至此,可以给出式(1)的计算过程:首先将双层优化模型经定理1转化为单层优化模型式(3),写出式(3)对应的矩SDP模型,实际计算中令基于矩的SDP模型中的s=1,并采用内点法求得对应SDP问题的矩解;再判断矩解是否满足全局最优的充分条件,若不满足则增大基于矩的SDP模型中的松弛阶次,即s=s+1,重新求解直到找到一个恰当的s满足全局最优条件;若满足全局最优的充分条件则进一步采用三阶段方法计算得到原问题的最优解[19]。具体实现方法见图 1。
3. 算例
将式(1)给出的一类描述TND-DUEC问题的一般双层优化模型框架用于最优道路收费问题(Optimal Toll Pricing Problem, OTPP)研究。常见的OTPP主要指道路拥挤改善收费和私有道路投资回收收费问题。在上述下层问题是确定性用户均衡问题的双层优化模型(式(1))框架下,其上层问题目标函数可以有不同的选择。对于道路拥挤改善收费,其目标函数通常设定为最小化总体旅行时间,而私有道路投资回收收费的目标则是最大化收费总收入。设式(1)中上层规划的决策变量ξ=(ξ1, ξ2, …, ξa, …, ξn1)T是施加于一组路段a∈A(A∈A)上的收费,la和ua分别为收费路段a∈A的收费下限和上限;下层变量η=(η1, η2, …, ηa, …, ηn2)T(a∈A)是在收费决策ξ下的均衡路段流量。基于式(1)的框架,常见的2类最优收费问题的上层规划目标函数Z可以表示为
\left\{ {\begin{array}{*{20}{l}} {\mathop {\max }\limits_\mathit{\boldsymbol{\xi }} Z = \sum\limits_{a \in \bar A} {{\xi _a}} {\eta _a}}&{私有道路投资回收收费}\\ {\mathop {\max }\limits_\mathit{\boldsymbol{\xi }} Z = \sum\limits_{a \in \bar A} {{t_a}} \left( {{\eta _a}} \right){\eta _a}}&{道路拥挤改善收费} \end{array}} \right. (25) 上层规划约束条件为
\left\{ {\begin{array}{*{20}{l}} {{l_a} \le {\xi _a} \le {u_a}}\\ {a \in \bar A}\\ {\bar A \in A} \end{array}} \right. (26) 下层规划目标函数z为
\mathop {\min }\limits_\mathit{\boldsymbol{\eta }} z = \sum\limits_{a \in A} {\int_0^{{\eta _a}} {{t_a}} } (\omega ){\rm{d}}\omega + \sum\limits_{a \in \bar A} {{\xi _a}} {\eta _a} (27) 下层规划的约束条件为
\sum\limits_{r \in {R_w}} {{h_{r, w}}} = {D_w}\;\;\;\;w \in W (28) {h_{r, w}} \ge 0 (29) {\eta _a} = \sum\limits_w {\sum\limits_r {{h_{r, w}}} } {\delta _{a, r, w}}\;\;\;\;\;a \in A (30) 对于每个给定的上层变量,下层变量是严格凸优化模型的解。
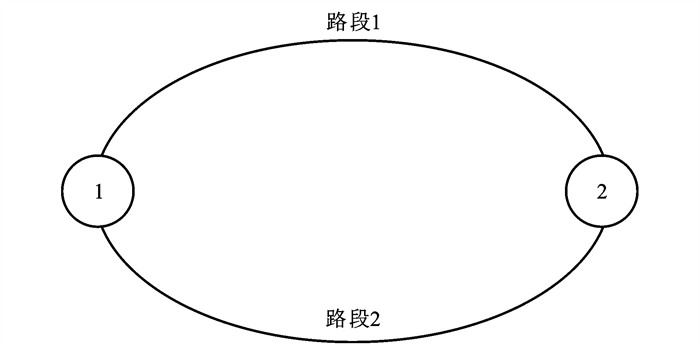
为了方便对比,直接引用文献[37]中使用的如图 2所示的简单网络,此网络由2个结点以及连接两结点的2条并行路段(路线)组成。图 2中:点1和点2分别为起点和终点;路段1是需要交费的快速路,其设计速度高,运行速度快;路段2是免费的非快速路,其道路等级低,设计速度低,车辆运行比较慢。
路段1、2的时间阻抗函数分别为
{{\rm{t}}_1}\left( {{\eta _1}} \right) = 2{\eta _1} + 2 (31) {{\rm{t}}_2}\left( {{\eta _2}} \right) = 4{\eta _2} + 8 (32) 假定从起点1到终点2的出行需求量是Dw=3。收费部门通过在路段1上收费ξ1而最大化收费总收入。假定在收费情况下,出行者满足用户均衡条件,单位流量收费ξ1以使收费总收入最大化可以用如下模型来表达
\mathop {\max }\limits_{{\xi _1}} Z = {\xi _1}{\eta _1} (33) 上层规划约束条件为
{\xi _1} \ge 0 (34) 下层规划目标函数为
\begin{array}{l} \mathop {\min }\limits_\mathit{\boldsymbol{\eta }} z = \int_0^{{\eta _1}} {(2\omega + 2)} {\rm{d}}\omega + \\ \;\;\;\;\;\;\;\;\;\int_0^{{\eta _2}} {(4\omega + 8)} {\rm{d}}\omega + {\xi _1}{\eta _1} \end{array} (35) 下层规划约束条件为
{\eta _1} + {\eta _2} = 3 (36) {\eta _1} \ge 0 (37) {\eta _2} \ge 0 (38) 式(34)~(38)满足定理1条件,应用定理1将双层优化问题式(34)~(38)转化为如下等价单层模型
\left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{{\xi _1}, {\eta _1}, {\lambda _0}, {\lambda _1}} Z = - {\xi _1}{\eta _1}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}{\xi _1} \ge 0}\\ {\;\;\;\;\;\;{\lambda _0}\left( {6{\eta _1} + {\xi _1} - 18} \right) - {\lambda _1} = 0}\\ {\;\;\;\;\;\;{\lambda _0}, {\lambda _1} \ge 0}\\ {\;\;\;\;\;\;\sum\limits_{j = 0}^1 {\lambda _j^2} = 1}\\ {\;\;\;\;\;\;{\lambda _1}{\eta _1} = 0}\\ {\;\;\;\;\;\;{\eta _1} \ge 0} \end{array}} \right. (39) 式(40)是一个非凸的最优化问题。文献[37]通过基于边际函数的方法解决了此双层优化问题TND-DUEC的不可导性问题,得到了此问题的局部解η1*=1.5,ξ1*=9,最大收费收入为p*=13.5元。
针对双层优化问题式(34)~(38)的等价单层模型式(39),本文采用Lasserre型半定松弛算法求解式(39)的等价半定规划模型,因矩矩阵的秩为1,满足前述全局最优解判定定理,故得到原双层多项式优化模型的解为全局最优解η1*=1.5,ξ1*=9(λ0=1,λ1=0),相应的最大收费收入为p*=13.5元。
与文献[37]中的结果比较,可以发现计算结果相同,但局部最优和全局最优的性质认定差别极大。且文献采用的方法需要实践第一线从业者难以掌握的较多技巧才能求解,而本文方法则显示出其程式化的直观与便利性。
4. 结语
(1) TND-DUEC问题的非凸性来源于交通分配均衡条件和非线性路段旅行时间函数。本文引入优化理论研究最新成果,建立一类面向典型交通网络设计问题的双层多项式优化模型,首次从理论上得到这类典型交通网络设计问题的全局最优解。本文模型的处理方法不仅能计算出全局最优解,甚至能找出所有的解。更重要的是,其有效性不依赖于任何的凸性假设。
(2) 从理论上给出了不同于以往求解一类道路收费问题的全局最优解方法。由于路段旅行时间函数通常采用的美国联邦公路局(Bureau of Public Road, BPR)函数为多项式函数,下层模型采用用户均衡约束是常见的基本形式,与已有相同主题的交通网络设计研究成果相比,本文研究结论具有一般性及推广价值。针对同一算例,通过与文献[37]使用的值函数方法得到的精确局部解算法的结果比较,表明本文方法从理论上保证了获得的是道路收费模型的全局最优解,相对于以往同一问题的研究是一个突破。
(3) 本文的双层优化问题属于乐观Stackelberg博弈问题,假定跟随者是合作的,因此,领导者可以选择成本最低的解决方案。若假定双层优化问题属于悲观Stackelberg博弈问题,即跟随者可能不合作,则领导者将需要为最坏的代价做准备。这在数学上是不同的,已有文献并未指出这种差异。需要指出的是,悲观Stackelberg博弈问题是一个更加困难且尚未得到深入研究的问题。
(4) 本文模型与算法用于小规模算例效果好。当应用于大规模问题时,会出现内存溢出情况。针对中等规模简单低阶多项式的情况验证了稀疏方法的可行性,后续工作是采用稀疏方法破解大规模网络带来的计算困难。
-
[1] FARAHANI R Z, MIANDOABCHI E, SZETO W Y, et al. A review of urban transportation network design problems[J]. European Journal of Operational Research, 2013, 229(2): 281-302. doi: 10.1016/j.ejor.2013.01.001 [2] BOYCE D E. Urban transportation network-equilibrium and design models: recent achievements and future prospects[J]. Environment and Planning A: Economy and Space, 1984, 16(11): 1445-1474. doi: 10.1068/a161445 [3] MAGNANTI T L, WONG R T. Network design and transportation planning: models and algorithms[J]. Transportation Science, 1984, 18(1): 1-55. doi: 10.1287/trsc.18.1.1 [4] FRIESZ T L. Transportation network equilibrium, design and aggregation: key developments and research opportunities[J]. Transportation Research Part A: General, 1985, 19(5/6): 413-427. [5] MIGDALAS A. Bilevel programming in traffic planning: models, methods and challenge[J]. Journal of Global Optimization, 1995, 7(4): 381-405. doi: 10.1007/BF01099649 [6] YANG Hai, BELL M G H. Models and algorithms for road network design: a review and some new developments[J]. Transport Reviews, 1998, 18(3): 257-278. doi: 10.1080/01441649808717016 [7] XU Xiang-dong, CHEN A, YANG Chao. A review of sustainable network design for road networks[J]. KSCE Journal of Civil Engineering, 2016, 20(3): 1084-1098. doi: 10.1007/s12205-016-1729-1 [8] MENG Qiang, YANG Hai. Benefit distribution and equity in road network design[J]. Transportation Research Part B: Methodological, 2002, 36(1): 19-35. doi: 10.1016/S0191-2615(00)00036-9 [9] GAO Zi-you, SUN Hui-jun, ZHANG Hao-zhi. A globally convergent algorithm for transportation continuous network design problem[J]. Optimization and Engineering, 2007, 8(3): 241-257. doi: 10.1007/s11081-007-9015-1 [10] WANG D Z W, LO H K. Global optimum of the linearized network design problem with equilibrium flows[J]. Transportation Research Part B: Methodological, 2010, 44(4): 482-492. doi: 10.1016/j.trb.2009.10.003 [11] YANG Hai, BELL M G H. A capacity paradox in network design and how to avoid it[J]. Transportation Research Part A: Policy and Practice, 1998, 32(7): 539-545. doi: 10.1016/S0965-8564(98)00017-2 [12] CHIOU S W. A hybrid approach for optimal design of signalized road network[J]. Applied Mathematical Modelling, 2008, 32(2): 195-207. doi: 10.1016/j.apm.2006.11.007 [13] YANG Hai. Sensitivity analysis for the elastic-demand network equilibrium problem with applications[J]. Transportation Research Part B: Methodological, 1997, 31(1): 55-70. doi: 10.1016/S0191-2615(96)00015-X [14] YANG Hai, SASAKI T, ⅡDA Y, et al. Estimation of origin -destination matrices from link traffic counts on congested networks[J]. Transportation Research Part B: Methodological, 1992, 26(6): 417-434. doi: 10.1016/0191-2615(92)90008-K [15] YANG Hai. Heuristic algorithms for the bilevel origin-destination matrix estimation problem[J]. Transportation Research Part B: Methodological, 1995, 29(4): 231-242. doi: 10.1016/0191-2615(95)00003-V [16] BEN-AYED O, BLAIR C E. Computational difficulties of bilevel linear programming[J]. Operations Research, 1990, 38(3): 556-560. doi: 10.1287/opre.38.3.556 [17] NIE Jia-wang, WANG Li, YE J J, et al. A Lagrange multiplier expression method for bilevel polynomial optimization[J]. SIAM Journal on Optimization, 2021, 31(3): 2368-2395. doi: 10.1137/20M1352375 [18] BEN-AYED O, BLAIR C E. Computational difficulties of bilevel linear programming[J]. Operations Research, 1990, 38(3): 556-560. doi: 10.1287/opre.38.3.556 [19] LAMPARIELLO L, SAGRATELLA S. A bridge between bilevel programs and Nash games[J]. Journal of Optimization Theory and Applications, 2017, 174(2): 613-635. doi: 10.1007/s10957-017-1109-0 [20] 高自友, 张好智, 孙会君. 城市交通网络设计问题中双层规划模型、方法及应用[J]. 交通运输系统工程与信息, 2004, 4(1): 35-44. doi: 10.3969/j.issn.1009-6744.2004.01.009GAO Zi-you, ZHANG Hao-zhi, SUN Hui-jun. Bi-level programming models, approaches and applications in urban transportation network design problems[J]. Communication and Transportation Systems Engineering and Information, 2004, 4(1): 35-44. (in Chinese) doi: 10.3969/j.issn.1009-6744.2004.01.009 [21] ABDULAAL M, LEBLANC L J. Continuous equilibrium network design models[J]. Transportation Research Part B: Methodological, 1979, 13(1): 19-32. doi: 10.1016/0191-2615(79)90004-3 [22] MARCOTTE P. Network optimization with continuous control parameters[J]. Transportation Science, 1983, 17(2): 181-197. doi: 10.1287/trsc.17.2.181 [23] DAVIS G A. Exact local solution of the continuous network design problem via stochastic user equilibrium assignment[J]. Transportation Research Part B: Methodological, 1994, 28(1): 61-75. doi: 10.1016/0191-2615(94)90031-0 [24] MIRRLEES J A. The theory of moral hazard and unobservable behaviour: Part Ⅰ[J]. The Review of Economic Studies, 1999, 66(1): 3-21. doi: 10.1111/1467-937X.00075 [25] DEMPE S, DUTTA J. Is bilevel programming a special case of a mathematical program with complementarity constraints?[J]. Mathematical Programming, 2012, 131(1/2): 37-48. [26] YE J J, ZHU Dao-li. Optimality conditions for bilevel programming problems[J]. Optimization, 1995, 33(1): 9-27. doi: 10.1080/02331939508844060 [27] YE J J, ZHU Dao-li. New necessary optimality conditions for bilevel programs by combining the MPEC and value function approaches[J]. SIAM Journal on Optimization, 2010, 20(4): 1885-1905. doi: 10.1137/080725088 [28] MENG Q, YANG H, BELL M G H. An equivalent continuously differentiable model and a locally convergent algorithm for the continuous network design problem[J]. Transportation Research Part B: Methodological, 2001, 35(1): 83-105. doi: 10.1016/S0191-2615(00)00016-3 [29] LI Chang-min, YANG Hai, ZHU Dao-li, et al. A global optimization method for continuous network design problems[J]. Transportation Research Part B: Methodological, 2012, 46(9): 1144-1158. doi: 10.1016/j.trb.2012.05.003 [30] JEYAKUMAR V, LASSERRE J B, LI G, et al. Convergent semidefinite programming relaxations for global bilevel polynomial optimization problems[J]. SIAM Journal on Optimization, 2016, 26(1): 753-780. doi: 10.1137/15M1017922 [31] PARRILO P A. Semidefinite programming relaxations for semialgebraic problems[J]. Mathematical Programming, 2003, 96(2): 293-320. doi: 10.1007/s10107-003-0387-5 [32] LASSERRE J B. Global optimization with polynomials and the problem of moments[J]. SIAM Journal on Optimization, 2001, 11(3): 796-817. doi: 10.1137/S1052623400366802 [33] CURTO R E, FIALKOW L A. Recursiveness, positivity, and truncated moment problems[J]. Houston Journal of Mathematics, 1991, 17(4): 603-635. [34] STURM J F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999, 11(1/2/3/4): 625-653. [35] TÜTÜNCÜ R H, TOH K C, TODD M J. Solving semidefinite -quadratic-linear programs using SDPT3[J]. Mathematical Programming, 2003, 95(2): 189-217. doi: 10.1007/s10107-002-0347-5 [36] HENRION D, LASSERRE J B. Detecting global optimality and extracting solutions in GloptiPoly[M]//HENRION D, GARULLI A. Positive Polynomials in Control: Lecture Notes in Control and Information Science. Berlin: Springer, 2005: 293-310. [37] 张小宁. 双层优化交通模型及其算法[J]. 同济大学学报(自然科学版), 2005, 33(2): 169-173. doi: 10.3321/j.issn:0253-374X.2005.02.007ZHANG Xiao-ning. Bi-level optimization in transportation analysis[J]. Journal of Tongji University (Natural Science), 2005, 33(2): 169-173. (in Chinese) doi: 10.3321/j.issn:0253-374X.2005.02.007 期刊类型引用(1)
1. 王飞,黄鹤. 智能网联汽车双车道主动换道优化规划仿真. 计算机仿真. 2024(07): 184-188 .  百度学术
百度学术其他类型引用(4)
-






 下载:
下载:

 下载:
下载:
 百度学术
百度学术


