Digital fatigue test of detail group at deck-U rib-diaphragm access hole of steel bridge deck in cable-stayed bridge
-
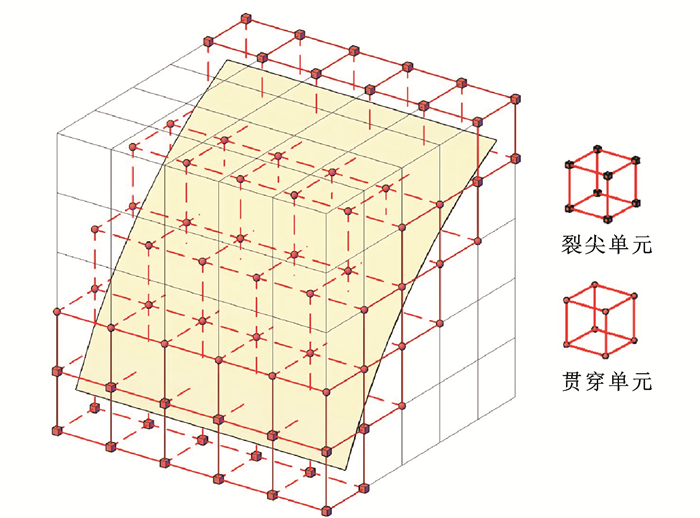
摘要: 为研究多场耦合作用下斜拉桥钢桥面板疲劳裂纹的扩展机理，建立了跨尺度斜拉桥全桥数字疲劳试验模型；通过模拟顶板-U肋-横隔板过焊孔细节群处多道焊缝的焊接全过程，将焊接残余应力引入数字疲劳试验模型中；基于扩展有限元法，在多场耦合作用下对顶板-U肋-横隔板过焊孔细节群处典型疲劳裂纹进行扩展机理的数字断裂参数分析与扩展行为的数字疲劳试验。研究结果表明：在顶板-U肋-横隔板过焊孔细节群处存在较大的残余拉应力，其最大值接近钢材的屈服强度，焊接残余应力对钢桥面板疲劳性能的影响不可忽略；后续焊缝会影响已有焊缝区域的应力场分布，在分析计算多道焊缝影响区域的焊接残余应力场时，需模拟多道焊缝的焊接全过程；在恒载应力场、活载应力场和焊接残余应力场的多场耦合作用下，按复合型裂纹扩展的工程准则，顶板-U肋-横隔板过焊孔细节群处4种典型疲劳裂纹的最大等效应力强度因子幅均大于疲劳裂纹扩展阈值，均将在疲劳循环荷载作用下发生疲劳扩展；在多场耦合作用下，过焊孔上方顶板-U肋连接焊缝的顶板侧焊趾处疲劳裂纹和U肋侧焊趾处疲劳裂纹均为以Ⅰ型裂纹为主导的Ⅰ-Ⅱ-Ⅲ型复合裂纹，Ⅱ型和Ⅲ型裂纹的影响不容忽略；过焊孔上方顶板-U肋连接焊缝的顶板侧焊根处疲劳裂纹和横隔板过焊孔边缘处疲劳裂纹均为Ⅰ型裂纹；建立的多场耦合作用下多尺度数字疲劳试验可为运营阶段大跨度桥梁钢桥面板疲劳裂纹的扩展提供分析与模拟方法。Abstract: To investigate the fatigue crack propagation mechanism of steel bridge deck in cable-stayed bridges under the multi-field coupling effect, a model for the multi-scale digital fatigue test of the whole cable-stayed bridge was constructed. The entire welding process of the multi-pass welds at the detail group at the deck-U rib-diaphragm access hole was simulated to introduce the welding residual stress into the model for the digital fatigue test. The digital fracture parameter analysis and the digital fatigue test were conducted under the multi-field coupling effect by the extended finite element method to clarify the propagation mechanism and propagation behavior of typical fatigue cracks of the detail group at the deck-U rib-diaphragm access hole. Research results show that the high residual tensile stress can be observed at the detail group at the deck-U rib-diaphragm access hole, with a maximum being close to the yield strength of steel. The influence of the welding residual stress on the fatigue performance of the steel bridge deck cannot be ignored. Subsequent welds affect the stress field distribution in the existing weld area. Therefore, the entire welding process needs to be simulated when the welding residual stress field in the influence range of multi-pass welds is analyzed and calculated. Under the multi-field coupling effect of dead-load stress field, live-load stress field and welding residual stress field, the maximum equivalent stress intensity factor ranges of four typical types of fatigue cracks of the detail group at the deck-U rib-diaphragm access hole are all larger than the fatigue crack propagation threshold according to the engineering criterion for the propagation of mixed cracks. In this case, the four types of fatigue cracks all propagate under the cyclic fatigue loading. Under the multi-field coupling effect, the fatigue cracks initiating from the deck-side weld toe of the deck-to-U rib welded joint above the access hole and those initiating from the U rib-side weld toe of the U rib-to-diaphragm welded joint are all mixed cracks of modes Ⅰ, Ⅱ, and Ⅲ dominated by mode-Ⅰ cracks. Nevertheless, the influences of mode-Ⅱ and mode-Ⅲ cracks cannot be overlooked. The fatigue cracks initiating from the deck-side weld root of the deck-to-U rib welded joint above the access hole and those initiating from the edge of the diaphragm access hole are all mode-Ⅰ cracks. The muti-scale digital fatigue test constructed under the multi-field coupling effect can provide analysis and simulation methods for the fatigue crack propagation in the steel bridge deck of a long-span bridge in operation. 1 tab, 28 figs, 32 refs.
-
图 1 扩展有限元法中含裂纹三维网格
Figure 1. Three-dimensional meshes with cracks in extended finite element method
图 2 正交异性钢桥面板构造尺寸(单位: mm)
Figure 2. Dimensions of orthotropic steel bridge deck (unit: mm)
图 3 跨尺度斜拉桥全桥数字疲劳试验模型
Figure 3. Multi-scale digital fatigue test model of whole cable-stayed bridge
图 10 顶板1/2截面纵向应力分布
Figure 10. Longitudinal stress distributions of deck at 1/2 section
图 13 顶板-U肋连接焊缝处残余应力分布
Figure 13. Residual stress distributions of deck-U rib welded joint
图 16 横纵向加载工况(单位：mm)
Figure 16. Horizontal and longitudinal loading conditions (unit: mm)
图 17 顶板侧焊趾处裂纹前缘短半轴方向Ke影响线
Figure 17. Influence lines of Ke along short half axis direction of crack front in weld toe of deck side
图 18 顶板侧焊根处裂纹前缘短半轴方向Ke影响线
Figure 18. Influence lines of Ke along short half axis direction of crack front in weld root of deck side
图 19 横隔板过焊孔边缘处裂纹前缘短半轴方向Ke的影响线
Figure 19. Influence lines of Ke along short half axis direction of crack front at edge of diaphragm access hole
图 20 U肋侧焊趾处裂纹前缘短半轴方向Ke的影响线
Figure 20. Influence lines of Ke along short half axis direction of crack front in weld toe of U-rib side
图 22 顶板侧焊趾处裂纹扩展的累计应变能释放率
Figure 22. Cumulative strain energy release rates of crack propagations in weld toe of deck side
图 24 顶板侧焊根处裂纹扩展的累计应变能释放率
Figure 24. Cumulative strain energy release rates of crack propagations in weld root of deck side
图 25 横隔板过焊孔边缘处疲劳裂纹扩展
Figure 25. Fatigue crack propagation at edge of diaphragm access hole
图 26 横隔板过焊孔边缘处裂纹扩展的累计应变能释放率
Figure 26. Cumulative strain energy release rates of crack propagations at edge of diaphragm access hole
图 28 U肋侧焊趾处裂纹扩展的累计应变能释放率
Figure 28. Cumulative strain energy release rates of crack propagations in weld toe of U-rib side
17. Influence lines of Ke along the direction of semi-minor axis of crack front at the weld toe on the deck side
18. Influence lines of Ke along the direction of semi-minor axis of crack front at the weld root on the deck side
19. Influence lines of Ke along the direction of semi-minor axis of crack front at the edge of the diaphragm access hole
20. Influence lines of Ke along the direction of semi-minor axis of crack front at the weld toe on the U-rib side
26. Cumulative SERRs for the propagation of cracks at the edge of the diaphragm access hole
表 1 焊接热输入与热源模型参数
Table 1. Parameters of welding heat input and heat source model
参数 顶板-U肋连接焊缝 顶板-横隔板连接焊缝 U肋-横隔板连接焊缝 熔宽/mm 10 11 6 熔深/mm 18 8 6 前轴长/mm 3 8 6 后轴长/mm 5 15 14 焊接速度/(mm·s-1) 5 5 4 电压/V 35 35 25 电流/A 280 310 250 
下载: 导出CSV
1. Parameters of welding heat input and heat source model
-
[1] 王春生, 冯亚成. 正交异性钢桥面板的疲劳研究综述[J]. 钢结构, 2009, 24(9): 10-13, 32. https://www.cnki.com.cn/Article/CJFDTOTAL-GJIG200909004.htmWANG Chun-sheng, FENG Ya-cheng. Review of fatigue research for orthotropic steel bridge decks[J]. Steel Construction, 2009, 24(9): 10-13, 32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GJIG200909004.htm [2] 张清华, 卜一之, 李乔. 正交异性钢桥面板疲劳问题的研究进展[J]. 中国公路学报, 2017, 30(3): 14-30, 39. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201703002.htmZHANG Qing-hua, BU Yi-zhi, LI Qiao. Review on fatigue problems of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2017, 30(3): 14-30, 39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201703002.htm [3] 王春生, 翟慕赛, HOUANKPO T O N. 正交异性钢桥面板典型细节疲劳强度研究[J]. 工程力学, 2020, 37(8): 102-111. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202008012.htmWANG Chun-sheng, ZHAI Mu-sai, HOUANKPO T O N. Fatigue strength of typical details in orthotropic steel bridge deck[J]. Engineering Mechanics, 2020, 37(8): 102-111. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202008012.htm [4] 王春生, 付炳宁, 张芹, 等. 正交异性钢桥面板足尺疲劳试验[J]. 中国公路学报, 2013, 26(2): 69-76. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201302011.htmWANG Chun-sheng, FU Bing-ning, ZHANG Qin, et al. Fatigue test on full-scale orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2013, 26(2): 69-76. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201302011.htm [5] WANG Chun-sheng, ZHAI Mu-sai, DUAN Lan, et al. Cold reinforcement and evaluation of steel bridges with fatigue cracks[J]. Journal of Bridge Engineering, 2018, 23(4): 04018014-1-11. [6] 段兰, 王春生, 翟慕赛, 等. 基于声发射技术的钢桥面板疲劳损伤监测与评估[J]. 交通运输工程学报, 2020, 20(1): 60-73. doi: 10.19818/j.cnki.1671-1637.2020.01.004DUAN Lan, WANG Chun-sheng, ZHAI Mu-sai, et al. Monitoring and evaluation of fatigue damage for orthotropic steel deck using acoustic emission technology[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 60-73. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2020.01.004 [7] SINGH I V, MISHRA B K, BHATTACHARYA S, et al. The numerical simulation of fatigue crack growth using extended finite element method[J]. International Journal of Fatigue, 2012, 36(1): 109-119. doi: 10.1016/j.ijfatigue.2011.08.010 [8] XIAO Zhi-gang, YAMADA K, YA S, et al. Stress analyses and fatigue evaluation of rib-to-deck joints in steel orthotropic decks[J]. International Journal of Fatigue, 2008, 30(8): 1387-1397. doi: 10.1016/j.ijfatigue.2007.10.008 [9] 朱劲松, 郭耀华. 正交异性钢桥面板疲劳裂纹扩展机理及数值模拟研究[J]. 振动与冲击, 2014, 33(14): 40-47, 71. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201414008.htmZHU Jin-song, GUO Yao-hua. Numerical simulation on fatigue crack growth of orthotropic steel highway bridge deck[J]. Journal of Vibration and Shock, 2014, 33(14): 40-47, 71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201414008.htm [10] 刘益铭, 张清华, 崔闯, 等. 正交异性钢桥面板三维疲劳裂纹扩展数值模拟方法[J]. 中国公路学报, 2016, 29(7): 89-95. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201607015.htmLIU Yi-ming, ZHANG Qing-hua, CUI Chuang, et al. Numerical simulation method for 3D fatigue crack propagation of orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2016, 29(7): 89-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201607015.htm [11] 王春生, 翟慕赛, 唐友明, 等. 钢桥面板疲劳裂纹耦合扩展机理的数值断裂力学模拟[J]. 中国公路学报, 2017, 30(3): 82-95. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201703009.htmWANG Chun-sheng, ZHAI Mu-sai, TANG You-ming, et al. Numerical fracture mechanical simulation of fatigue crack coupled propagation mechanism for steel bridge deck[J]. China Journal of Highway and Transport, 2017, 30(3): 82-95. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201703009.htm [12] DA SILVA A L L, CORREIRA J A F O, DE JESUS A M P, et al. Influence of fillet end geometry on fatigue behaviour of welded joints[J]. International Journal of Fatigue, 2019, 123: 196-212. doi: 10.1016/j.ijfatigue.2019.02.025 [13] 赵秋, 吴冲. U肋加劲板焊接残余应力数值模拟分析[J]. 工程力学, 2012, 29(8): 262-268. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201208042.htmZHAO Qiu, WU Chong. Numerical analysis of welding residual stress of U-rib stiffened plate[J]. Engineering Mechanics, 2012, 29(8): 262-268. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201208042.htm [14] VAN DEN BERG N, XIN Hao-hui, VELJKOVIC M, et al. Effects of residual stresses on fatigue crack propagation of an orthotropic steel bridge deck[J]. Materials and Design, 2021, 198: 109294. [15] 李爱群, 司政, 邓扬, 等. 钢桥面横隔板与U肋焊接处残余应力场分析[J]. 桥梁建设, 2019, 49(6): 36-41. https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201906007.htmLI Ai-qun, SI Zheng, DENG Yang, et al. Analysis of residual stress field in welding joints between diaphragms and U ribs of steel bridge deck[J]. Bridge Construction, 2019, 49(6): 36-41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QLJS201906007.htm [16] WANG Chun-sheng, WANG Yu-zhu, CUI Bing, et al. Numerical simulation of distortion-induced fatigue crack growth using extended finite element method[J]. Structure and Infrastructure Engineering, 2020, 16(1): 106-122. [17] 孙正华, 李兆霞, 陈鸿天. 大跨斜拉桥结构行为一致多尺度有限元模拟[J]. 中国公路学报, 2009, 22(5): 68-74, 117. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200905010.htmSUN Zheng-hua, LI Zhao-xia, CHEN Hong-tian. Concurrent multi-scale finite element modeling of long-span cable-stayed bridge[J]. China Journal of Highway and Transport, 2009, 22(5): 68-74, 117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200905010.htm [18] YAN Fei, CHEN Wei-zhen, LIN Zhi-bin. Prediction of fatigue life of welded details in cable-stayed orthotropic steel deck bridges[J]. Engineering Structures, 2016, 127: 344-358. [19] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620. [20] MOËS N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1): 131-150. [21] MELENK J M, BABUSKA I. The partition of unity finite element method: basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1/2/3/4): 289-314. [22] 孟建兵, 徐文骥, 董小娟, 等. 基于多物理环境顺序耦合法的联合弧特性分析[J]. 焊接学报, 2011, 32(8): 57-60, 116. https://www.cnki.com.cn/Article/CJFDTOTAL-HJXB201108016.htmMENG Jian-bing, XU Wen-ji, DONG Xiao-juan, et al. Characteristics analysis of combined plasma arc based on sequential coupling method of physics environment approach[J]. Transactions of the China Welding Institution, 2011, 32(8): 57-60, 116. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJXB201108016.htm [23] 杨文, 石永久, 王元清, 等. 结构钢焊接残余应力三维有限元分析[J]. 吉林大学学报(工学版), 2007, 37(2): 347-352. https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY200702019.htmYANG Wen, SHI Yong-jiu, WANG Yuan-qing, et al. Three-dimensional finite element analysis on welding residual stresses of construction steel[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(2): 347-352. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JLGY200702019.htm [24] 程久欢, 陈俐, 于有生. 焊接热源模型的研究进展[J]. 焊接技术, 2004, 33(1): 13-15. https://www.cnki.com.cn/Article/CJFDTOTAL-HSJJ200401006.htmCHENG Jiu-huan, CHEN Li, YU You-sheng. Research progress of welding heat source model[J]. Welding Technology, 2004, 33(1): 13-15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HSJJ200401006.htm [25] GOLDAK J, CHAKRAVARTI A, BIBBY M. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2): 299-305. [26] 吴冲, 刘海燕, 张志宏, 等. 桥面铺装温度对正交异性钢桥面板疲劳的影响[J]. 同济大学学报(自然科学版), 2013, 41(8): 1213-1218. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201308017.htmWU Chong, LIU Hai-yan, ZHANG Zhi-hong, et al. Influence of pavements temperature on fatigue life of orthotropic deck of steel bridge[J]. Journal of Tongji University (Natural Science), 2013, 41(8): 1213-1218. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201308017.htm [27] 李丽娟, 崔闯, 卜一之, 等. 铺装层对正交异性钢桥面板疲劳性能影响效应研究[J]. 世界桥梁, 2016, 44(5): 48-52. https://www.cnki.com.cn/Article/CJFDTOTAL-GWQL201605010.htmLI Li-juan, CUI Chuang, BU Yi-zhi, et al. Study of influential effects of pavement on fatigue performance of orthotropic steel deck plate[J]. World Bridges, 2016, 44(5): 48-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GWQL201605010.htm [28] 王春生, 翟慕赛, HOUANKPO T N O, 等. 正交异性钢桥面板冷维护技术及评价方法[J]. 中国公路学报, 2016, 29(8): 50-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201608007.htmWANG Chun-sheng, ZHAI Mu-sai, HOUANKPO T N O, et al. Cold maintenance technique and assessment method for orthotropic steel bridge deck[J]. China Journal of Highway and Transport, 2016, 29(8): 50-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201608007.htm [29] SIH G C. Strain-energy-density factor applied to mixed mode crack problems[J]. International Journal of Fracture, 1974, 10(3): 305-321. [30] 金建三, 李润方. 工程断裂力学[J]. 重庆大学学报(自然科学版), 1978, 1(4): 79-119. https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE197804006.htmJIN Jian-san, LI Run-fang. Engineering fracture mechanics[J]. Journal of Chongqing University (Natural Science), 1978, 1(4): 79-119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FIVE197804006.htm [31] PARIS P C, ERDOGAN F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering, 1963, 85(4): 528-533. [32] CHANG Jun, XU Jin-quan, MUTOH Y. A general mixed-mode brittle fracture criterion for cracked materials[J]. Engineering Fracture Mechanics, 2006, 73(9): 1249-1263. -
点击查看大图
计量
- 文章访问数: 939
- HTML全文浏览量: 401
- PDF下载量: 141
- 被引次数: 0
