0.   引言

钢轨在投入使用后，顶面沿轨道延长方向出现波浪形不均匀磨耗现象，简称波磨。磨耗严重的位置形成波谷，轨面光带明显变宽；磨耗轻微的位置形成波峰，轨面光带稍窄。随着列车运营速度的提升，因波磨激励轮轨振动而引发的问题日益突出，比如环境噪声污染、车辆动力损耗、车辆轨道部件疲劳破损、增加线路维护工作量和维修成本等。如不及时整治，波磨会恶化轮轨关系，降低车辆运行品质，严重时甚至引发轨道结构局部破坏进而危及行车安全。波磨现象广泛地存在于轨道交通中，一直是困扰铁路行业的重点技术难题。国际上尚未形成具有普遍性的波磨成因理论，部分研究成果能够解释特定类型波磨的萌生、发展。Grassie等^[1-3]在总结既有波磨发展文献及其个人研究成果的基础上，根据波磨特点按照波长(频率)固定机理与损伤机理将波磨分为6大类：Pinned-Pinned共振型、车辙槽型、重载型、轻轨型、P2力共振型以及其他特殊轨道结构的波磨，并对各种类型的波磨形成机理、预防对策、整治措施等进行了探讨；金学松等^[4]综述了近年来波磨研究成果，依据轮轨振动在波磨形成过程中的力学行为将波磨形成机理归纳为自激振动理论^[5-6]、反馈振动理论^[7-8]以及其他接触疲劳、腐蚀磨损、残余应力等理论，讨论了改善轮轨作用关系的抑制波磨措施，如摩擦调节器^[9]、轨道吸振器^[10]、轨面打磨等方法的应用效果。在精准识别波磨区段的基础上，国际铁路行业标准Acoustics—Railway Applications—Measurement of Noise Emitted by Railbound Vehicles(ISO 3095:2013(E)) 采用轨面粗糙度水平作为评价波磨严重程度的依据，而中国《高速铁路无砟轨道线路维修规则》(TG/GW 115—2012)将波磨谷深作为评判钢轨伤损程度和制订整治决策的量度。

相对于人工上道直接测量波磨谷深的作业方式，车载设备能够高效、客观地识别波磨从而广泛地应用于线路监测中，比如采用激光摄像技术^[11]直接测量轨面廓形通过信号处理手段提取波磨特征，采用超声波和涡流检测^[12]、车体加速度^[13]、轴箱振动加速度^{[1-3, 14-15]}和测力轮对^[16-22]等技术通过波磨响应特性辨识波磨状态。轮轨垂向力能直接反映运行过程中轮对力学行为，其高频成分是波磨评价和演化预测的重要参数^[16-17]，因此，轮轨垂向力广泛地应用在波磨监测中。Nielsen^[18]采用Rayleigh-Timoshenko模拟轨道理论分析了黏弹性垫板下钢轨振动模态，找出轨面粗糙度与轮轨垂向力在频域上的映射关系，现场调查了实测轮轨垂向力峰值大于160 kN时波磨区段粗糙度，提出了速度为160和197 km·h^-1条件下轮轨垂向力最小截止频率，验证轮轨垂向力峰值，识别了波长为40~80 mm波磨病害的有效性；为刻画波磨激励的轮轨响应特征，选用500~1 350 Hz频段上轮轨垂向力的有效值作为特征指标，并给出了轮轨垂向力有效值与轨面粗糙度之间的函数表达式^[19]。Gullers等^[20]结合上述函数表式与150~200 km·h^-1时轨面粗糙度管理值逆向反推轮轨垂向力有效值监控阈值，为测力轮对技术在波磨识别、制订维修措施等提供依据。中国高铁线路上检测车的型式多样，为减少检测车辆静轮载对评价结果的影响，李谷等^[21]通过分析振动频率500~1 350 Hz轮轨垂向附加力有效值监测评价速度为200 km·h^-1以上高铁线路直线和大半径曲线上的波磨状态，从“振动能量”的角度衡量波磨病害的严重程度^[22]，采用轮轨垂向附加力有效值指标时程数据评价钢轨波磨发展状态与打磨整治作业效果。波磨区段轨面不平顺具有准周期性，波长和谷深是其2个特征量。波长是轮轨相互作用敏感因素^[23-24]，直接和轮轨垂向力强弱与振动频段相关。在波磨波长成分单一的条件下，谷深较小时轮轨垂向力与谷深近似线性关系，采用轮轨垂向力峰值或有效值能够有效地评价波磨；在谷深较大或者波磨波长成分多样时，直接利用轮轨垂向力峰值或有效值评价波磨将有失准确。而既有研究成果多依据轮轨垂向力峰值或有效值评价波磨严重程度，较少考虑波长因素的影响，因此，开展轮轨垂向力随波磨波长变化规律的研究有助于深化认识波磨激励特性，探索出科学合理的基于测力轮对评价波磨状态的监测技术。

本文采用显式有限元法，以典型服役车辆参数建立三维轮轨动力学模型，细化钢轨波磨模型，由实测轮轨垂向力验证模型有效性，仿真了300 km·h^-1时不同波磨工况下轮轨垂向力变化特征；引入轨面不平顺变化率表征波磨状态，利用非线性最小二乘法和非理式方程拟合了轮轨垂向力与轨面不平顺变化率之间的函数关系，给出了拟合系数随波长变化曲线，分析了钢轨振动模态对拟合参数的影响；在此基础上，提出了基于轮轨垂向力估算波磨谷深的方法，以现场试用效果验证该估算方法的可行性。

1.   轮轨动力学模型构建

1.1   模型构建

车辆通过波磨区段时轮轨垂向相互作用的激励频率f为

式中：v为车辆运行速度；λ为波磨波长。

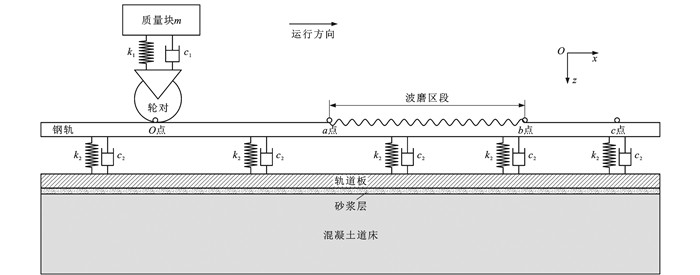
由式(1)可知：在λ为40~180 mm，v大于250 km·h^-1时，f大于385.8 Hz，该频段的轮轨垂向力响应特性与车辆一系悬挂装置、构架、车体等部件运动关系较小^[25]。在构建轮轨动力学模型研究直线工况下钢轨波磨区段轮轨垂向振动特性时可将车辆一系悬挂装置与以上部件简化为质量块m，而车辆一系悬挂系统简化为垂向和横向弹簧单元施加在轮对端部，如图 1所示。将轮对起始位置O点设置为坐标系原点，x轴正方向为车辆运行方向，车辆沿z轴沉浮运动且向下为正，y轴正方向利用右手定则确定。Oa段钢轨为开始运动区段，中间ab段为波磨区段，c点为仿真结束位置。车辆一系悬挂由质量块m与轮对之间刚度为k₁、阻尼为c₁的面弹簧模拟，约束轮对和质量块横向运动，底部设置1∶40轨底坡，端部施加面对称约束以减少模型中钢轨长度对计算结果的影响；扣件对钢轨垂向支承作用由图 1中刚度为k₂、阻尼为c₂的面弹簧模拟，约束钢轨与扣件接触位置的横向和纵向自由度。轮对通过波磨区段的运行时间较短，因此，在仿真计算过程中不考虑轮对侧滚、横移等影响，模型中包括单股轨道和半个轮对。

图  1  轮轨动力学模型结构

Figure  1.  Structure of wheel-rail dynamics model

下载: 全尺寸图片 幻灯片

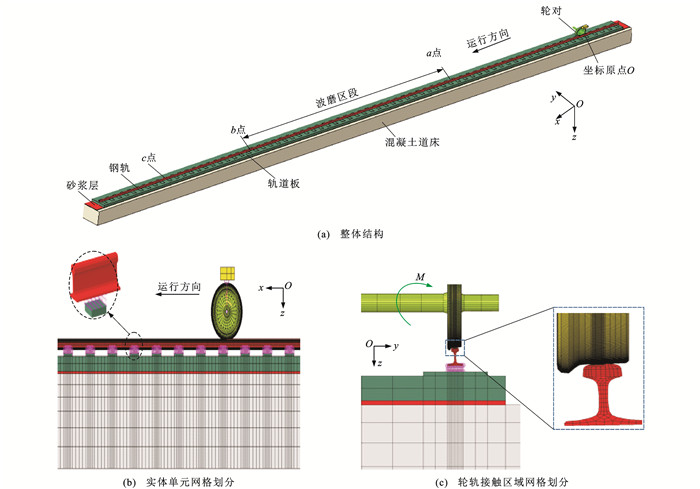
轮轨动力学模型中轨道长度为46. 66 m，包含72组轨枕，轨枕间距为650 mm，整体结构如图 2(a)所示。车轮和钢轨分别采用380B型拖车车轮LM_B型踏面和CN60型钢轨廓形的真实几何尺寸建模，采用双线性本构方程模拟轮轨材料弹塑变形性能。每组面弹簧由5×11个弹簧组成，如图 2(b)所示。

图  2  轮轨动力学模型实体单元构成与网格划分

Figure  2.  Solid element composition and mesh of wheel-rail dynamics model

下载: 全尺寸图片 幻灯片

为缩减轮轨动力学模型的规模和计算时间，实体单元划分网格的尺寸与单元所在区域的关注程度有关，靠近轮轨接触区域的网格尺寸较小，在钢轨端部、轮轴、CA砂浆层、道床等远离轮轨接触区域的实体单元网格尺寸较大。在轮轨接触面上采用正六面体单元划分网格，最小尺寸设置为2 mm×2 mm× 2 mm，M为牵引扭矩，如图 2(c)所示。

在轮轨接触面法线方向采用“面-面”硬接触算法仿真轮轨法向接触力，切线方向采用干燥条件下的轮轨相互作用状态，库伦摩擦因数设为0.3^[26]。为减少ABAQUS显式算法求解轮轨动力学模型达到动态平衡所需时间，先采用隐式算法计算重力载荷下模型静平衡状态，并将其作为显式仿真的初始边界条件。在轮对上施加速度载荷，运行至钢轨a点时模型应处于动态平衡状态。在车轮上施加牵引扭矩M以减少轮轨摩擦力对运行速度的影响，确保轮对匀速运行。牵引扭矩M^[27]为

式中：F_x、F_n分别为轮轨力沿x轴、接触面法线n方向上的分量；R为轮对滚动圆半径；J为轮对转动惯量；μ为牵引系数，取0.03^[28]；ε为轮对角加速度，车辆匀速运行时有ε≈0。

ABAQUS显式算法采用中心差分法显式求解轮轨实时运动状态和接触力，每个时间增量步结束时刻的状态完全由该增量步开始时刻的位移、速度、加速度计算得到^[29]。最大积分时间步长Δt由有限元模型最高固有频率ω_max决定，满足

式中：ζ为轮轨系统临界阻尼比；E为轮轨材料弹性模量；ρ为轮轨材料密度；L_e为单元中最小的网格尺寸。

图 2所示轮轨动力学模型最小网格尺寸为2 mm时，Δt取值为10^-7 s数量级。该模型能够输出极短时间内的轮轨接触力、位移等物理量，从而可以模拟波磨高频激励下轮轨动力学行为。

1.2   波磨模型

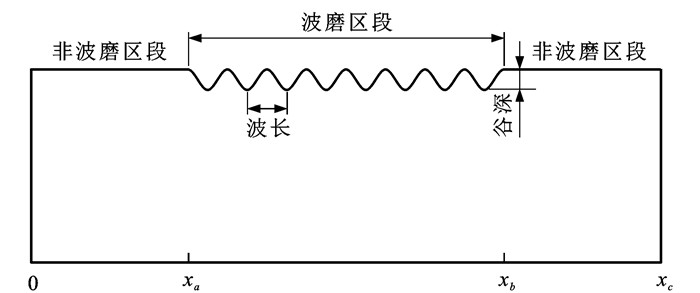
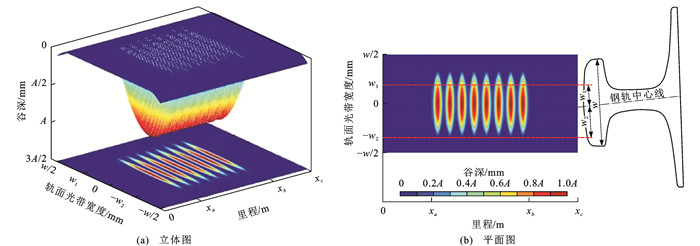
钢轨波磨是由多种波长成分的轨面不平顺叠加而成，波磨激励轮轨振动特性中也包含多种频率成分，但特定高铁区段上的运营车辆型式、运营速度、轨道类型等相对稳定，易形成以固定波长为主^[1-3]的波磨病害，钢轨顶部呈现等波长连续多个轨面不平顺，因此，轮轨动力学模型波磨区段施加余弦形轨面不平顺，如图 3所示，x_a和x_b为图 1中波磨区段起点a和终点b的x轴坐标，x_c为仿真结束位置的x轴坐标。

图  3  波磨区段轨面不平顺

Figure  3.  Rail surface irregularity in corrugation section

下载: 全尺寸图片 幻灯片

由图 3可知，波磨区段轨面不平顺Δ(x, y, z)随节点位置x呈现周期性变化，即

式中：A为谷深。

轨道横截面平行于坐标系yOz平面，采用抛物线形式修正轨面不平顺，修正系数δ(x, y, z)为

式中：w_x是波磨沿y轴分布的宽度，即图 4中轨面光带宽度的一半。

图  4  波磨区段轨面光带宽度

Figure  4.  Light band width on rail surface in corrugation section

下载: 全尺寸图片 幻灯片

一般情况下，w_x小于CN60钢轨轨头宽度w。由图 4可知轨面光带宽度沿x轴变化周期与波磨波长一致，采用余弦函数模拟波磨区段轨面光带宽度沿横向(y轴)变化特征，即

式中：w₁、w₂为钢轨光带最窄、最宽处宽度的半值，下文分别取15、20 mm。

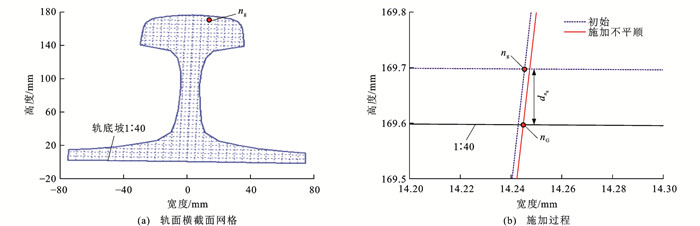
通过修改波磨区段单元网格节点坐标的方式施加轨面不平顺，轨道ab段任一网格节点n_g(x_g, y_g, z_g) 的修正量为d_ng时施加波磨后节点坐标n_G(x_G, y_G, z_G)为

式中：θ为1∶40轨道坡角度；h为CN60型钢轨高度，取176 mm。

在图 2模型波磨区段施加轨面不平顺过程中网格节点坐标变换过程如图 5所示。

图  5  波磨区段轨面不平顺施加过程

Figure  5.  Applied process of rail surface irregularity in corrugation section

下载: 全尺寸图片 幻灯片

综合式(4)~(7)，轮轨动力学模型中波磨区段钢轨顶部沿着x轴方向呈现连续余弦形，沿y轴方向呈现抛物线分布。施加波磨后的钢轨表面状态如图 6所示，图中颜色越深表示谷深越大，蓝色表示正常轨面。

图  6  波磨区段钢轨表面状态

Figure  6.  Rail surface state in corrugation section

下载: 全尺寸图片 幻灯片

2.   模型验证

图 2所建模型参数来源于CRTSⅡ型无砟轨道与CRH3型服役动车组，主要参数如表 1所示。

表  1  轮轨动力学模型主要参数

Table  1.  Main parameters of wheel-rail dynamics model

参数名称		量值	参数名称		量值
轮轨材料	泊松比	0.30	一系悬挂弹簧(垂向)	刚度/(kN·mm-1)	1.04
	密度/(mg·mm-3)	7.8		阻尼/(N·s·mm-1)	50.0
	弹性模量/GPa	210.0	一系悬挂弹簧(横向)	刚度/(kN·mm-1)	0.40
	切线模量/GPa	21.0		阻尼/(N·s·mm-1)	60.0
	屈服强度/MPa	800.0	扣件支承弹簧(垂向)	刚度/(kN·mm-1)	22.00
轨道板	泊松比	0.25		阻尼/(N·s·mm-1)	47.7
	密度/(mg·mm-3)	2.4	每米钢轨质量/kg		60.643
	弹性模量/GPa	34.5	车体等部件等效质量/103 kg		14
CA砂浆材料	泊松比	0.20	混凝土道床材料	泊松比	0.16
	密度/(mg·mm-3)	1.6		密度/(mg·mm-3)	2.4
	弹性模量/GPa	8.0		弹性模量/GPa	32.5
静轮重P0/kN		70.3	轨枕间距Lr/mm		650.0
轮轨间摩擦因数		0.30	轮对滚动圆半径/mm		430

下载: 导出CSV 

| 显示表格

通过实测验证的方式证明图 2轮轨动力学模型仿真的准确性。某CRH3型高速综合检测列车拖车安装有测力轮对，实时输出轮轨间高频接触力^{[17, 19]}，输出频率为4 000 Hz，轮轨力检测系统架构示意图如图 7所示。测力轮对作为特殊传感器，应保持良好的圆顺状态，减少车轮高阶不圆顺激励的高频成分对测试结果的影响，确保数据质量。

图  7  轮轨力检测系统

Figure  7.  Wheel-rail force detection system

下载: 全尺寸图片 幻灯片

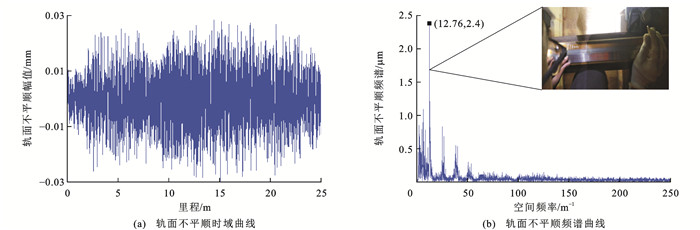
某高铁存在长度约为25 m的波磨区段，人工上道测试的轨面不平顺如图 8(a)所示，采样间隔为2 mm，轨面不平顺幅值位于±0.03 mm；其频谱曲线存在能量集中特征，如图 8(b)所示，频谱能量最大值对应的空间频率为12.76 m^-1，其倍频如25.51、38.64、51.03 m^-1等处也存在局部峰值，但频谱能量较小，说明该波磨区段存在固定波长的主要成分，由基频可知主要波长约为78 mm。波磨现场测试情况如图 8(b)右上侧所示。

图  8  波磨区段轨面不平顺实测的时频域特征

Figure  8.  Measured time-frequency domain characteristics of rail surface irregularity in corrugation section

下载: 全尺寸图片 幻灯片

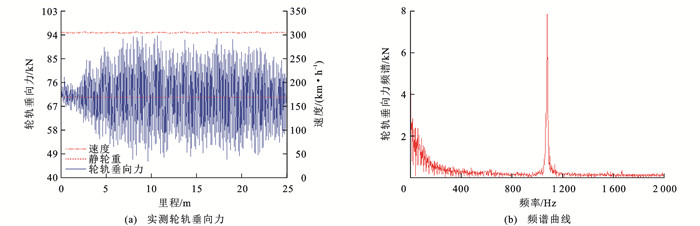
轮轨力检测系统在图 8(a)所示波磨区段上实测轮轨垂向力与速度曲线如图 9(a)所示，可知：轮轨垂向力在静轮重P₀附近波动且随着谷深的增加波动范围逐步增大，在4.7 m左右时波动范围固定在±23 kN。轮轨垂向力频谱曲线在1 083 Hz存在局部峰值，如图 9(b)所示，该局部峰值对应图 8(b)中钢轨波磨主要成分波长激励频率。

图  9  波磨区段实测轮轨垂向力与频谱

Figure  9.  Measured wheel-rail vertical force and its spectrum in corrugation section

下载: 全尺寸图片 幻灯片

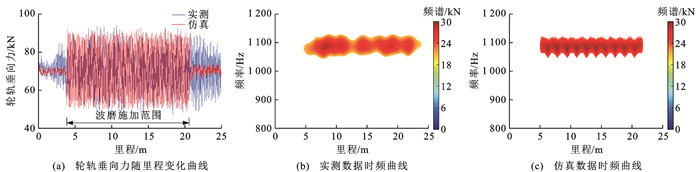
限于仿真计算规模，将图 8(a)中4.7~22.3 m轨面不平顺施加在轮轨动力学模型中以对比稳定状态的轮轨垂向力，输出频率为10 kHz。为与图 7所示轮轨力检测系统实测数据对比，先对输出结果4 kHz低通滤波，轮轨垂向力仿真与实测结果对比如图 10(a)所示，可知：波磨区段轮轨垂向力仿真数据与实测结果在时频域上的变化特征趋势一致，幅值相当；图中左侧为未施加波磨的区域，轮轨垂向力在静轮重P₀附近存在的小幅度波动是由轨枕对钢轨不连续支承作用引起的。时频曲线能够显示轮轨垂向力随里程和频率分布的特性^[30]，两者时频分布分别如图 10(b)、(c)所示，图中颜色的强弱代表对应里程和频率上主要轮轨垂向力能量成分的大小。由图 10(b)可知：实测轮轨垂向力主要成分集中在3个频段，即0(静轮重)、125和1 081 Hz，其中1 081 Hz对应图 8(a)中的波磨激励频率。对比可知：在低频段，轮轨垂向力仿真输出与实测结果在频域分布差异较大，但在高频段，两者分布规律吻合良好，说明图 2所示轮轨动力学模型能够用以仿真研究波磨激励下轮轨垂向力高频响应特性。

图  10  实测与仿真轮轨垂向力时频域曲线对比

Figure  10.  Comparison of measured and simulated time-frequency domain curves of wheel-rail vertical force

下载: 全尺寸图片 幻灯片

3.   仿真与拟合结果分析

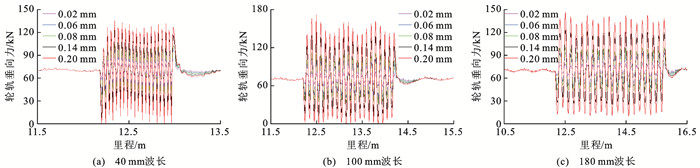
某CRTSⅡ型高铁线路上钢轨波磨波长大多集中在80~120 mm^[21]，谷深不大于0.2 mm。下文研究中波长范围设置为40~180 mm，谷深变化范围较大。速度为300 km·h^-1条件下，λ分别为40、100、180 mm，A分别为0.02、0.06、0.08、0.14、0.20 mm的波磨激励下轮轨垂向力波形分别如图 11(a)~(c)所示。图 11(a)与11(b)中部分工况最小轮轨垂向力为0，此时轮轨之间脱离了接触。

图  11  不同工况下轮轨垂向力波形

Figure  11.  Wheel-rail vertical force waveforms under different load cases

下载: 全尺寸图片 幻灯片

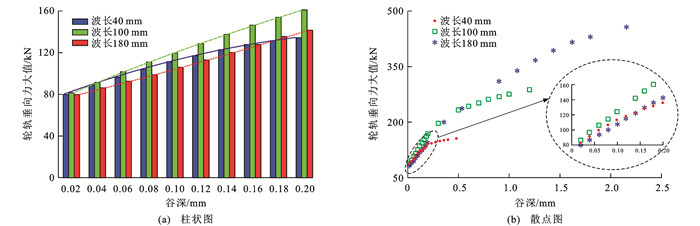
由图 11可知：连续余弦形波磨激励的轮轨垂向力呈周期性变化，其波动范围均随A的增加而增大；A不变时轮轨垂向力波动范围与波长λ关系复杂，如A为0.2 mm时，上述3种波长对应的轮轨垂向力波动范围分别为0.0~125.4、0.0~159.5和13.3~142.1 kN；λ为100 mm时轮轨垂向力波动范围明显比其他波长工况下结果大；因受轨枕不连续支承作用、轮轨接触位置等因素的影响，每个周期的轮轨垂向力波形略有差异。单个轮轨垂向力大值不能很好地表征波磨引起轮轨动态响应特性，下文选用波磨区段轮轨垂向力3σ大值F作为衡量波磨激励响应指标。为简洁表达起见，波长为λ时对应的轮轨垂向力大值记为F_λ。图 12(a)为图 11所示轮轨垂向力大值F柱状图，曲线为轮轨垂向力大值F随谷深A变化趋势线。

图  12  不同工况下轮轨垂向力大值与谷深关系曲线

Figure  12.  Relation curves between large value of wheel-rail vertical force and valley depth under different load cases

下载: 全尺寸图片 幻灯片

由图 12(a)可知：λ、A均影响轮轨垂向力大值F的分布，如在A小于0.18 mm，λ等于40 mm时，轮轨垂向力大值F₄₀大于F₁₈₀而小于F₁₀₀，在A大于0.18 mm时，F₁₈₀小于F₁₀₀而大于F₄₀。而针对相同轮轨垂向力响应，不同波磨波长对应的谷深也不相同，由图 12(a)拟合曲线可知，λ分别为40、100、180 mm，A分别为0.08、0.06、0.10 mm时轮轨垂向力大值F均为100 kN。

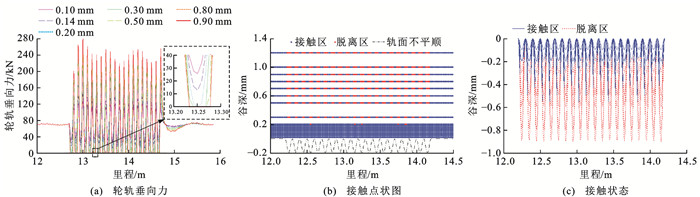
谷深A继续增加时上述波长工况下F随A变化的散点图如图 12(b)所示，可知：3种波长下的散点具有相似的分布特征，A较小时F随A增加近似线性增大，A较大时F随A增加的增速趋于平缓，且F随A的增速与λ有关。该现象与不同波磨工况下轮轨接触状态的变化有关，λ为100 mm，在A分别为0.10、0.14、0.20 mm等时的轮轨垂向力波形如图 13(a)所示。

图  13  波长为100 mm时轮轨垂向力与轮轨接触状态

Figure  13.  Wheel-rail vertical force and contact state when wavelength is 100 mm

下载: 全尺寸图片 幻灯片

由图 11(b)和图 13(a)可知：A大于0.2 mm时在部分区段轮轨垂向力最小值为0，说明轮轨之间脱离接触，采用不同的颜色区分波磨区段上轮轨接触和脱离状态，其中轮轨脱离区域网格节点标记为红色，轮轨接触区域网格节点标记为蓝色；A小于0.2 mm时轮轨垂向力最小值均大于0，轮轨不脱离接触，整个波磨区段上网格均为蓝色；在A为0.2 mm时部分区域出现轮轨脱离现象，如图 13(b)中纵坐标为0.2 mm对应横线上孤立的红点所示；A增加到0.3 mm时图 13(a)轮轨垂向力最小值为0的区域增多，相应的图 13(b)中纵坐标为0.3 mm的横线上红点区域的个数增加，几乎每个波磨周期内均存在轮轨脱离接触的区域；A增加到0.5 mm时每个波磨周期内均出现红点，且同一个周期内红点的数量也在增加；A继续增加时图 13(b)对应横线上红点的个数和区域不再增加，说明轮轨脱离接触的区域相对固定，随A的变化较小。图 13(c)表示轮轨接触位置随波磨区段轨面不平顺的变化情况，A小于0.2 mm时轨面不平顺上网格节点全为蓝色，说明在此条件下轮轨未脱离接触；随着A由0.2 mm增加到0.9 mm时轮轨接触位置逐渐集中在波峰附近，且A大于0.5 mm时轮轨接触区域变化不大，此时轮轨垂向力波形随A的增加变化较小，对应图 12中轮轨垂向力大值F受A影响相对较小。波磨区段轨面不平顺近似呈周期性变化，相位变化范围为-π~π，将波峰位置记作0，则轮轨接触区域处于-0.36π~0.54π之间，涵盖长度约为0.9λ。

定义轨面不平顺变化率ξ为谷深与波长的比值，即

速度为300 km·h^-1时F₄₀、F₁₀₀、F₁₈₀与ξ之间的散点如图 14所示。

图  14  不同波长下F-ξ拟合曲线

Figure  14.  F-ξ fitting curves under different wavelengths

下载: 全尺寸图片 幻灯片

利用有理式方程和非线性最小二乘方法^[31]拟合图 14中F与ξ的函数关系，有理式方程为

式中：c₁、c₂和d₁为待定拟合参数。

在拟合优度^[31]不小于0.995前提下，由式(9)得到F₄₀、F₁₀₀、F₁₈₀分别与ξ之间的拟合曲线如图 14所示，拟合系数见圈选位置，3组拟合方程的误差均方值分别为0.89、1.70和1.59 kN。由图 14可知：F与ξ之间拟合曲线与散点趋势相同，拟合优度高，且拟合误差均方值较小，说明式(9)能够表征两者之间的映射关系。

由式(9)拟合波长40 ~180 mm时F与ξ之间的函数关系，拟合参数c₁、c₂和d₁的取值如表 2所示。

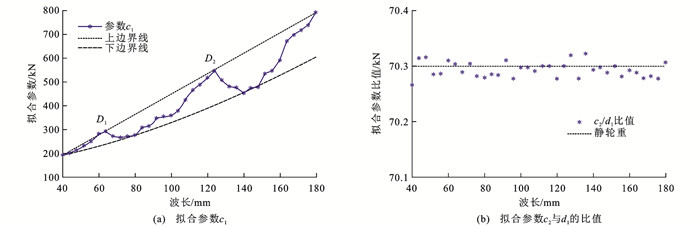
表  2  不同波长下F-ξ拟合参数取值

Table  2.  F-ξ fitting coefficient values under different

波长/mm	c1/kN	c2/kN	d1	波长/mm	c1/kN	c2/kN	d1
40	190.16	0.238 34	0.003 392	112	466.24	0.441 16	0.006 275
44	198.34	0.240 00	0.003 413	116	486.19	0.459 11	0.006 531
48	213.48	0.204 86	0.002 914	120	516.26	0.383 93	0.005 463
52	231.26	0.219 18	0.003 119	124	547.69	0.513 41	0.007 303
56	247.65	0.304 35	0.004 330	128	507.14	0.451 08	0.006 415
60	281.49	0.289 32	0.004 115	132	479.73	0.415 85	0.005 917
64	291.72	0.323 53	0.004 602	136	474.99	0.402 18	0.005 719
68	271.85	0.283 64	0.004 035	140	454.06	0.355 97	0.005 064
72	265.65	0.245 71	0.003 495	144	472.66	0.393 95	0.005 604
76	270.60	0.207 42	0.002 951	148	478.18	0.364 31	0.005 183
80	275.31	0.219 93	0.003 129	152	534.69	0.454 41	0.006 464
84	307.18	0.238 77	0.003 397	156	545.05	0.392 93	0.005 591
88	312.87	0.217 15	0.003 090	160	589.44	0.469 87	0.006 685
92	347.68	0.312 53	0.004 445	164	672.34	0.557 96	0.007 938
96	354.75	0.289 67	0.004 122	168	697.12	0.555 45	0.007 904
100	358.74	0.288 72	0.004 107	172	717.96	0.544 23	0.007 744
104	377.34	0.301 22	0.004 285	176	739.86	0.559 40	0.007 960
108	423.57	0.357 60	0.005 088	180	792.30	0.566 50	0.008 057

下载: 导出CSV 

| 显示表格

由式(9)可知：波磨轻微时ξ较小，激励的高频轮轨垂向力也较小，在ξ≈0时F取值近似等于拟合参数c₂与d₁的比值，其值大小趋近于静轮重P₀，如图 10、11所示，未施加波磨时轮轨垂向力在静轮重P₀附近波动；波磨程度严重时ξ值较大，ξ取值越大，F取值越趋近于拟合参数c₁。表 2中拟合参数c₁及c₂与d₁的比值随波长变化的散点图如图 15所示。

图  15  拟合参数随波长变化

Figure  15.  Fitting parameters changing with wavelength

下载: 全尺寸图片 幻灯片

由图 15(a)可知：拟合参数c₁整体上随着波磨波长的增加而增大，在图中虚线所示的上下边界内波动；波长在68~72、120~136 mm时曲线上存在局部峰值，如图中D₁、D₂位置所示，D₁、D₂位置出现局部峰值的原因与钢轨固有振动频率有关。D₁位置对应的频率接近钢轨Pinned-Pinned共振频率f_p，此时轨道振动波形驻波节点位于轨枕支承位置，波长等于2倍轨枕跨距，f_p为^[32]

式中：n为Pinned-Pinned共振频率阶数；m_r为单位长度钢轨质量；I为截面惯性矩。

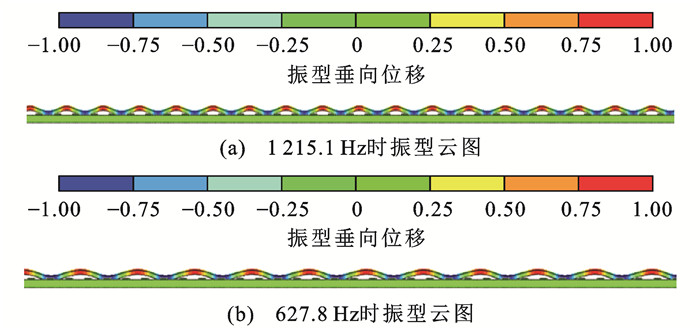
由式(10)与表 1中模型参数可知：EI 取6.62× 10⁶ N·m²，当n=1时1阶钢轨Pinned-Pinned共振频率f_p约为1 227.8 Hz，其半频为613.9 Hz，对应轨道振型波长约等于3倍轨枕跨距。图 2轮轨动力学模型中钢轨Pinned-Pinned共振频率约为1 215.1 Hz，与式(10)计算结果较为接近。

车辆运行速度为300 km·h^-1，波长在68~72、120~136 mm范围内波磨激励轮轨振动频率由式(1)计算可知分别为1 157.4~1 225.5、612.7~694.4 Hz，该频段与钢轨Pinned-Pinned共振频率及其半值相接近，轮轨间发生接触共振，两者之间的相互作用增强，轮轨垂向力及其大值均增大，造成该波长对应拟合系数c₁偏大。图 2中轨道模型在1 215.1 Hz及其半频627.8 Hz时的模态振型如图 16所示，图中颜色表示振型向量方向和相对大小，钢轨Pinned-Pinned共振波形波长为2个轨枕跨长，驻点位于轨枕上。

图  16  钢轨模态振型云图

Figure  16.  Nephograms of rail vibration modes

下载: 全尺寸图片 幻灯片

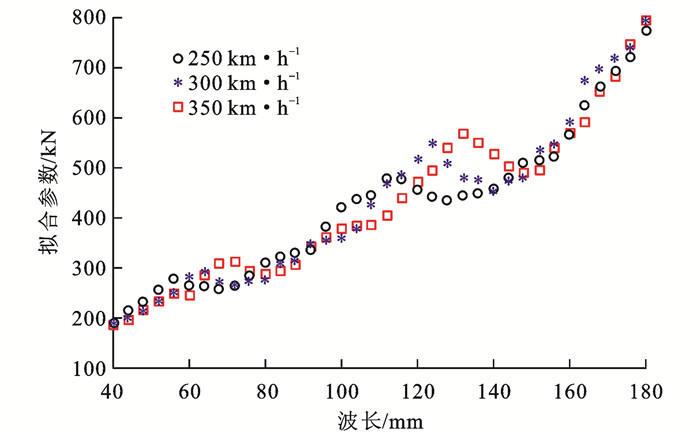
波磨激励频率接近钢轨Pinned-Pinned共振频率及其半频时，拟合参数c₁曲线上出现局部峰值，而由式(1)可知波磨激励频率相对不变时车辆运行速度与波长成正比，拟合参数c₁出现局部峰值对应的频段随着车辆运行速度的增加而增大。速度为250、300、350 km·h^-1条件下F与ξ拟合方程参数c₁随波长变化的散点如图 17所示。

图  17  不同速度条件下c₁随波长变化曲线

Figure  17.  Changing curves of c₁ with wavelength under different velocity conditions

下载: 全尺寸图片 幻灯片

4.   谷深估算

F与ξ拟合方程式(9)可转换为

F可写为静轮重P₀与轮轨垂向动态附加力P_d之和^[33]，即

由图 15(b)可知：拟合参数c₂与d₁的比值近似等于静轮重P₀，式(11)可写为

由式(12)、(13)可得

由式(8)、(14)可得谷深估算值$\hat{A}$为

由式(15)可知：谷深估算中系数c₁、d₁均与波长λ有关。利用傅里叶变换^[34]或希尔伯特-黄变换^[30]等时频转换技术将轮轨垂向力时域信号转换为频域信号，找出轮轨垂向力信号能量主频，再由式(1)和车辆运行速度估算波长λ。

波磨区段存在多种波长成分时，根据轮轨垂向力频域幅值大小顺序排列波长λ，依次定义为λ₁、λ₂、…λ_m，此时，$\hat{A}$可记为各波磨成分谷深估算值的和，即

式中：m为波磨区段波长成分的个数；$\hat{A}_i$为第i个波磨谷深估算值。

由式(15)可得$\hat{A}_i$

式中：λ_i为第i个成分的波长; d_{1, i}、c_{1, i}为与波长λ_i对应的F-ξ拟合系数；P_{d, i}为与波长λ_i波磨成分相关的动态附加垂向力最大值。

m为$\hat{A}$参与计算的成分总数目，其值与$\hat{A}_m$的大小有关。当$\hat{A}_m$小于波磨整治谷深限值^[9]的5 %时，结束式(17)的叠加计算。表 2中给出了300 km·h^-1时部分波长对应的拟合参数c₁、d₁，40~180 mm范围内其他波长的拟合参数可由表 2数据插值得到。

5.   估算方法验证

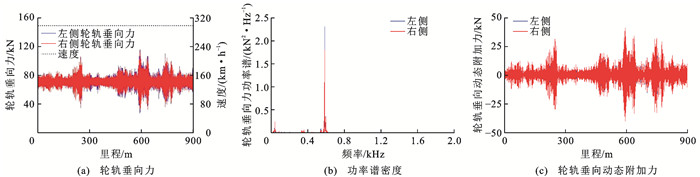
某CRTSⅡ型板式无砟轨道线路上轮轨垂向力实测波形与功率谱密度曲线如图 18所示，由图 18(a)可知：左右股钢轨上均存在多处波磨区段，在570~640 m范围内的波磨激励的轮轨垂向力幅值最大。图 18(b)中左右侧轮轨垂向力功率谱曲线在588.4 Hz存在峰值，由式(1)及运行速度299 km·h^-1可得该波磨主要成分波长约为141 mm。通过带通滤波的方式获得轮轨动态附加垂向力P_d如图 18(c)所示，左侧轮轨垂向力在里程600 m附近的最大值约为113.9 kN，P_d值为43.31 kN。根据表 2线数据性插值得到波长141 mm时拟合参数c_{1, 141}和d_{1, 141}，再由式(17)计算谷深估算值$\hat{A}$约为0.092 mm。

图  18  轮轨垂向力、功率谱密度与附加轮轨垂向力

Figure  18.  Wheel-rail vertical forces, power spectral densities and additional vertical forces

下载: 全尺寸图片 幻灯片

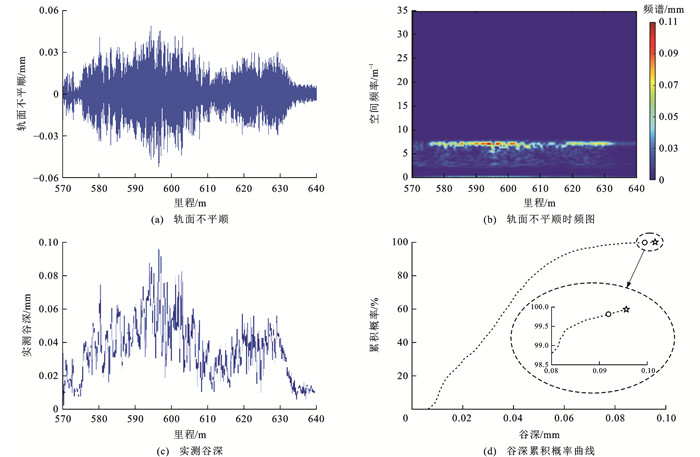
相应钢轨波磨区段轨面不平顺及其时频图如图 19所示，时频图 19(b)中红色颜色对应波磨区主要波长成分；图中能量集中频段7.1 m^-1对应的空间波长约为141 mm，速度为299 km·h^-1下该波长的激励频率为589 Hz，与图 18(b)中频谱主频一致。

图  19  实测轨面不平顺与谷深累积曲线

Figure  19.  Measured rail surface irregularity and valley depth accumulated curves

下载: 全尺寸图片 幻灯片

该波磨区段谷深随里程分布与累积概率曲线如图 19(c)和图 19(d)所示。由图 19(c)可知：里程为590~605 m时谷深均大于0.08 mm，最大谷深为0.096 mm，与谷深估算值$\hat{A}$比较接近，分别如图 19(d)中五角星和圆形所示。

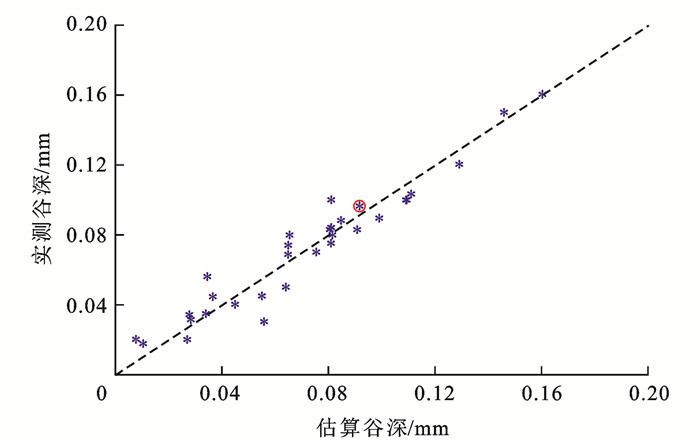
采用式(17)与实测轮轨垂向力在某高铁上共检测出32个谷深估算值$\hat{A}$大于0.01 mm区段。32个谷深估算值$\hat{A}$与实测谷深A散点图如图 20所示，图中圈选对比样本为图 18、19结果；A与$\hat{A}$相关系数约为0.97，两者之间具有较强的线性相关性；图中散点越靠近图中虚线$\hat{A}$=A，$\hat{A}$与A的差异越小。

图  20  波磨样本中A-$\hat{A}$散点图

Figure  20.  A-$\hat{A}$scatter plot in corrugation samples

下载: 全尺寸图片 幻灯片

图 20中32个波磨样本中A与$\hat{A}$均方误差约为0.010 mm；在$\hat{A}$大于0.08 mm时，A与$\hat{A}$之间均方误差约为0.008 mm。高速铁路线路维修规则^[9]中波磨整治限度为谷深A大于0.08 mm，采用误判率E_p对本文算法用于波磨整治决策的可行性进行评价，即

式中：p为波磨整治限值，取0.08 mm；$N_{\hat{A}>p}$为$\hat{A}$大于p的样本个数；$N_{\hat{A}>p, A<p}$为在$\hat{A}$大于p的前提下A小于p的样本个数。

由图 20与式(18)可知：基于本文估算波A ∧方法进行波磨整治决策时的误判率E_p为6.25%，说明该方法用于钢轨打磨决策时具有较好的适用性。

谷深估算值$\hat{A}$还受到轨道几何不平顺、轮轨匹配、车轮不圆顺度与轮轨力测试精度等多种因素的影响，为降低因$\hat{A}$估算误差而可能引起的波磨状态误判，在应用实践中选取$\hat{A}$不小于0.07 mm作为上道复核预警门限值。

6.   结语

(1) 轮轨垂向力、谷深映射关系与波磨波长有关，如波磨激励轮轨垂向力为100 kN时，波磨波长分别40、100、180 mm时对应的谷深依次为0.08、0.06、0.10 mm，所以采用轮轨垂向力评价钢轨波磨状态时波长是必须考虑的因素之一。

(2) 在拟合优度大于0.995时采用非线性最小二乘法与有理式拟合F与ξ关系曲线，拟合系数c₁值为波长固定时F随谷深增大时趋近的固定值；系数c₂与d₁的比值约等于静轮重P₀。c₁整体上随着波长的增加而增大，受钢轨振动模态影响c₁在部分波长时呈现局部极值特征。速度为300 km·h^-1时波长在68~72、120~136 mm区段c₁出现局部极值，激励频率接近钢轨Pinned-Pinned共振频率及其半值。

(3) 基于轮轨垂向力估算波磨谷深$\hat{A}$的方法在某高铁上试用，对比32个波磨区段的谷深$\hat{A}$与实测谷深A样本，结果表明：A与$\hat{A}$之间相关系数为0.97，两者具有较强的线性相关性；在$\hat{A}$大于0.08 mm时两者均方差较小，说明A与$\hat{A}$在数值上比较接近。采用本文方法为钢轨打磨整治决策时的误判率E_p约为6.25%，说明该方法能够用于波磨谷深的估算，从而为波磨整治决策提供支撑。

(4) 中国高铁线路结构复杂，运营车型多样。本文仿真背景相对简单，所提估算方法仍在高铁线路波磨状态监测实践中试用，继续积累波磨现场轮轨垂向力、谷深等测试数据，为进一步改进和优化波磨评价算法提供了数据基础，拟基于仿真分析和实测数据研究不同轨道类型和车辆参数下参数c₁、d₁分布规律，进而提出具有普适性的基于轮轨垂向力评判波磨状态的方法，为钢轨打磨提供决策参考。