0.   引言

随着高速铁路运行速度和轴重的不断提升，轮轨磨耗问题日益凸显，影响高速列车行车安全^[1]。升力翼高速列车突破了传统气动外形，通过安装升力翼，为高速行驶的列车提供足够的升力，减小轮轨作用力，实现了车辆等效轻量化，提高了列车轮轨使用周期。

目前，升力翼列车尚处于探索阶段，研究成果较少。王瑞东等^[2]基于列车限界，探讨了升力翼高度和攻角对气动布局的影响，优化了串联翼布局下的二维翼型，但由于列车周围流场呈现复杂的三维非定常特性，二维简化模型还是存在很大的局限性；戴志远等^[3]提出在磁悬浮列车尾车上安装升力翼以减小尾车气动升力，研究了升力翼角度和数量对列车气动性能的影响。这些研究偏向于探索安装升力后列车的气动力变化，而车体外形改变后的流场特征尚未有详细描述。此外，随着列车运行速度的提高，列车风给站台乘客、轨旁工人及附近建筑物带来的安全问题越来越凸显^[4-6]，因而，列车风效应成为重要研究内容。朱春丽等^[7]采用分离涡模拟(Detached Eddy Simulation, DES)方法研究了缩尺比为1∶8的高速列车模型的列车风特性，强调了列车顶部边界层厚度沿列车长度变化对受电弓设备周围流场结构的影响；Bell等^[8]研究表明列车风速度峰值大多出现在近尾迹区，且认为该现象与尾涡的非定常特性有关；潘永琛等^[9]采用不同涡旋识别方法研究了近尾流区的涡旋结构，发现尾车附近围绕着高涡量的强涡旋；Xia等^[10]基于数值模拟方法研究了地面构型对列车风和尾迹的影响，发现固定地面条件下列车风速度更大且尾涡振荡更剧烈，提出尾迹附近的大尺度纵向涡与较高的列车风速度相关。另一方面，不少学者研究表明，列车风和尾流主要受列车几何形状影响。Guo等^[11]比较了缩尺比为1∶20的单双车编组列车的列车风速，指出双编组模型在车旁同一位置的速度峰值及远尾迹区速度都要远大于单编组模型；Chen等^[12]利用改进型延迟分离涡模拟(Improved Delayed Detached Eddy Simulation, IDDES)方法研究了不同头部流线型长度列车的气动性能，发现流线型长度越短，列车风速度越大，纵向涡强度越高。可见，列车风速度分布和尾迹湍流特征对研究列车流场特性有重要意义，而升力翼对列车风及尾涡产生和演化带来的影响尚不明确。

基于此，本文开展了时速400 km升力翼高速列车列车风及尾迹湍流特性的相关研究。为达到理想的减重效果并兼顾一定的气动效率，结合现有成果^[2]，以带13个升力翼的高速列车为研究对象，基于IDDES方法，对比了有无升力翼下高速列车的时均列车风速度分布特征及尾流涡旋结构，并结合尾流的速度频率分析了尾涡结构的瞬态特性，为未来升力翼高速列车的深入研究和开发提供关键理论与数据支撑。

1.   数值模拟方法

1.1   几何模型

为了降低计算成本和减小计算周期^[13]，选取缩尺比为1∶10的三车编组某型CRH高速列车为计算模型，以车高H作为特征长度，H为0.389 m，列车尺寸为19.7H(长L)×0.84H(宽W)×1.0H(高)，在不影响计算准确度的前提下对其外形进行简化处理，忽略车门、车窗、受电弓等复杂细部结构，保留列车典型的气动外形。

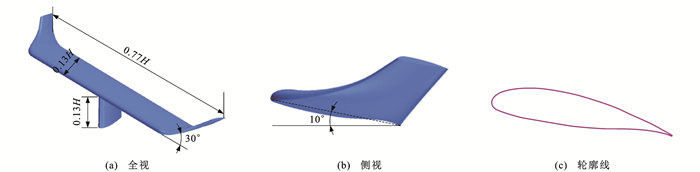
翼尖涡使气流产生下洗效果，从而产生诱导阻力，而翼梢小翼不仅可以增加有效翼展，而且能大幅度降低翼尖涡的涡旋强度，提高其耗散效率^[14]，因此，升力翼翼型为融合式翼梢小翼结构，弦长为0.13H，展长为0.77H，上反角为30°，攻角为10°，支撑柱高度为0.13H，沿列车纵向中心对称面对称布置，升力翼尺寸见图 1。

图  1  升力翼几何参数

Figure  1.  Geometric parameters of lift airfoil

下载: 全尺寸图片 幻灯片

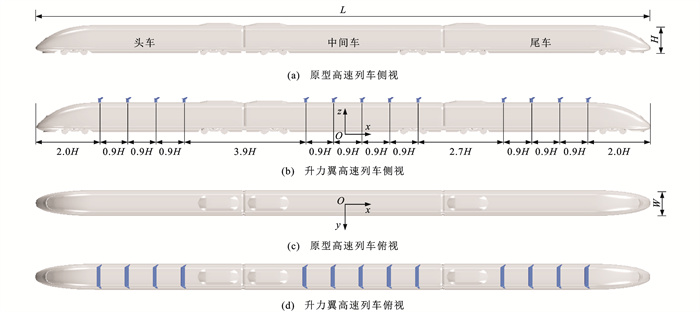
为了研究升力翼对高速列车周围流场的影响，探讨高速列车有无升力翼2种工况。具体几何模型如图 2所示，工况1是不添加升力翼的原型列车，工况2是沿列车纵向中心对称面布置13个升力翼的列车，考虑到需达到一定的等效减重效果且兼顾列车的头尾对称，选择在头尾车分别布置4个翼，中间车布置5个翼的布局方式，同一节车厢上的相邻升力翼相距0.9H。坐标原点O位于列车流向和展向的中心位置，高度与轨顶齐平，沿流向方向为x轴正方向，沿展向方向为y轴正方向，垂直向上为z轴正方向。根据标准轨距铁路限界标准，桥隧限界为距轨面7 250 mm，该高度的对应宽度为4 000 mm左右，当前布置方案满足限界要求。

图  2  数值计算模型

Figure  2.  Numerical calculation models

下载: 全尺寸图片 幻灯片

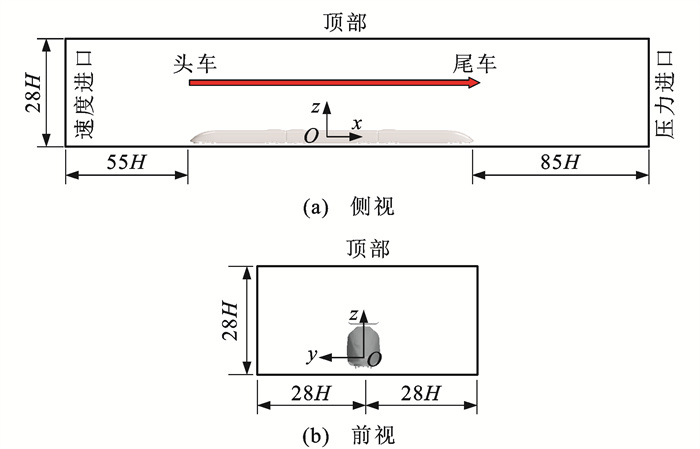
1.2   计算域和边界条件

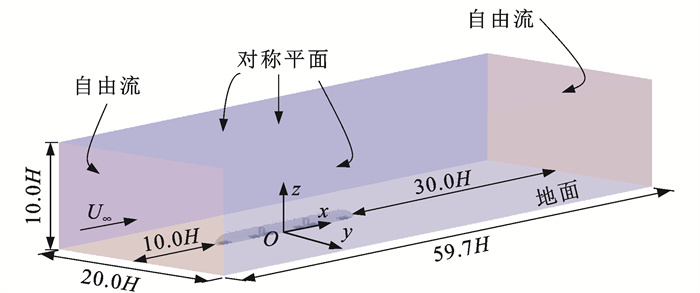
计算域和边界条件设置如图 3所示。计算域长为59.7H，宽为20H，高为10H，列车底部与地面的距离为0.05H，入口距离列车头车鼻尖点10H，出口距离尾车鼻尖点30H，两侧距离列车模型10H，该尺寸足以保证列车周围流场充分发展^[12]。计算域进出口均设置为自由流，其速度U_∞为111.11 m·s^-1，转化成马赫数为0.33，顶面和两侧设置为对称平面。为了模拟真实情况下列车与地面的相对运动，地面设置为移动壁面，其运动速度等于自由流速度，其余边界设置为无滑移壁面。雷诺数R_e为2.9×10⁶。2种工况均采用上述相同的参数设置。

图  3  计算域几何尺寸和边界条件

Figure  3.  Geometric dimensions and boundary conditions of computational domain

下载: 全尺寸图片 幻灯片

1.3   网格划分

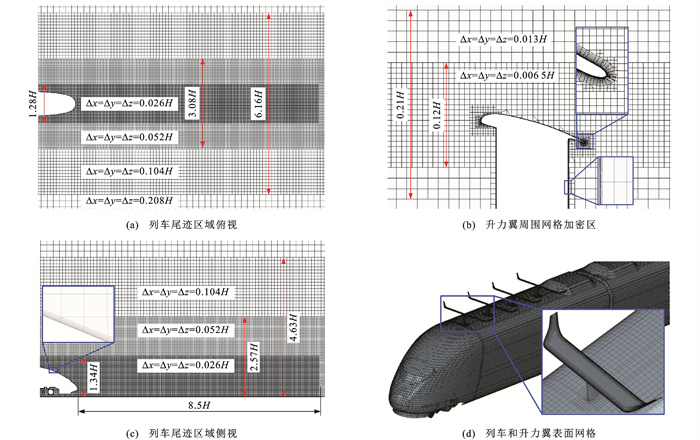
计算区域采用结构化六面体网格进行离散，车体表面、升力翼和转向架分别设置18、12和8层棱柱层，增长率均为1.1。为了准确模拟车身周围流动情况且以尽可能少的计算量求解流场，对车身、尾迹区和升力翼周围等区域进行网格加密处理。为了保证精度相同，对于原型列车和升力翼列车2种工况，计算模型采用相同的方法进行离散。列车模型周围网格的空间分布情况如图 4(a)和(c)所示，升力翼周围的加密区如图 4(b)所示，高速列车及升力翼表面网格如图 4(d)所示，其中：Δx、Δy和Δz分别为沿x、y和z方向的单位网格长度。

图  4  数值计算网格(中网格)

Figure  4.  Numerical calculating meshes (medium mesh)

下载: 全尺寸图片 幻灯片

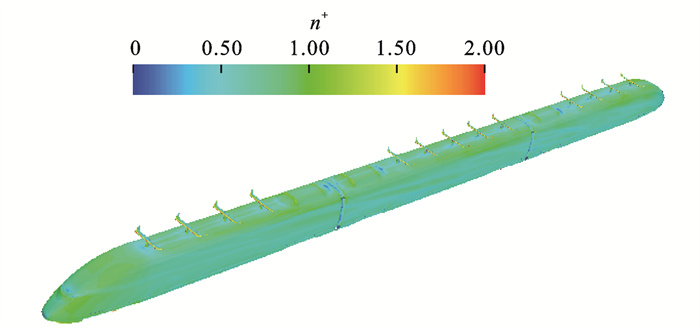
针对原型高速列车生成3组粗、中、细网格进行网格独立性研究，网格数分别为2 000万、3 500万和4 800万。表 1为计算网格的具体分布信息，其中：n⁺为壁面量纲一距离；y⁺为沿y方向的量纲一距离；x⁺为沿x方向的量纲一距离。3组网格的n⁺都设置为1，以满足边界层区域内速度梯度的充分发展，列车表面n⁺分布见图 5。

表  1  数值计算网格信息

Table  1.  Numerical calculating meshes information

网格	n+	y+	x+	网格数量/万
粗	1	340	340	2 000
中	1	320	320	3 500
细	1	280	280	4 800

下载: 导出CSV 

| 显示表格

图  5  升力翼高速列车表面n⁺分布

Figure  5.  Distribution of n⁺ for high-speed train with lift airfoils

下载: 全尺寸图片 幻灯片

为保证仿真结果不会随网格尺度变密而改变，需要进行网格无关性验证。考虑到在实际运行中，地面保持固定，列车移动，而在数值模拟中，采用列车坐标系代替地面固定坐标系，赋予地面与来流速度相等的速度来模拟列车与地面的相对运动，因此，需要将数值计算得到的瞬时速度转化成以地面为参考系的速度，并用来流速度进行归一化处理，本文参考Bell等^[8]提出的列车风速度定义方式，具体为

式中：U_GF为地面坐标系下x向列车风速度；U_TF为列车坐标系下x向数值计算速度；V_GF为地面坐标系下y向列车风速度；V_TF为列车坐标系下y向数值计算速度；U_h为合成列车风速度。

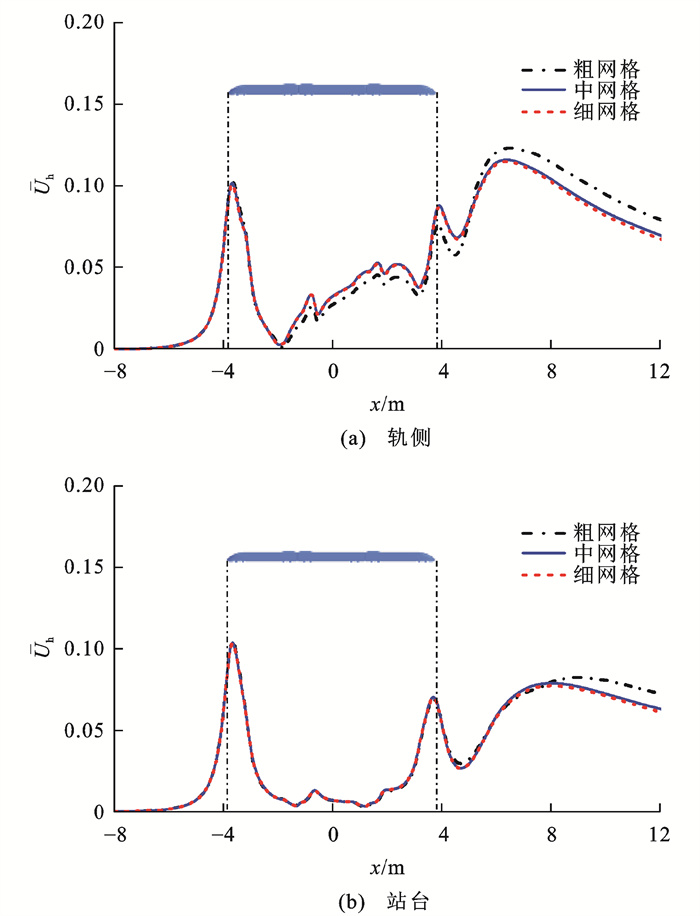
图 6展示了用3组网格计算得到的原型列车时均列车风速度$\bar{U}_{\mathrm{h}}$在欧盟铁路互联互通技术规范(Technical Specification for Interoperability, TSI)中要求的2个监测位置(轨侧和站台)的分布情况，其中轨侧和站台分别距离轨顶0.2和1.4 m，距离轨道中心3.0 m。从图 6中可以看出，3组网格计算得到的时均列车风速度曲线整体趋势相近，且该分布规律与Wang等^[15]计算得到的列车风速度变化趋势类似。由图 6可见，粗网格无法准确捕捉列车周围的流动分离特性，在列车尾迹区域出现较大差异，而中网格与细网格的时均列车风速度曲线几乎重合，表明二者计算结果非常接近。综合考虑时间成本和数值精度，选取中网格用于后续计算。

图  6  三组网格的时均列车风速度分布

Figure  6.  Distributions of time-averaged slipstream velocities with three sets of meshes

下载: 全尺寸图片 幻灯片

1.4   数值算法

采用基于湍动能(k)-单位湍动能耗散率(ω)模型的剪切应力输运(Shear Stress Transport, SST)两方程湍流模型，结合IDDES混合方法求解Navier-Stokes(NS)方程。SST k-ω湍流模型由Menter^[16]提出，在近壁面附近湍流模拟精度较高。IDDES方法是一种雷诺平均NS(Reynolds Averaged Navier-Stokes, RANS)和大涡模拟(Large Eddy Simulation, LES)的混合方法，结合了延迟分离涡模拟(Delayed Detached Eddy Simulation, DDES)和壁面模化大涡模拟(Wall-Modelled Large Eddy Simulation, WMLES)的优点^[17]，其中DDES方法是在DES方法的基础上引入一个延迟函数，保证在边界层内采用RANS方法进行求解^[18]，而WMLES模型则减少了对雷诺数的依赖性。

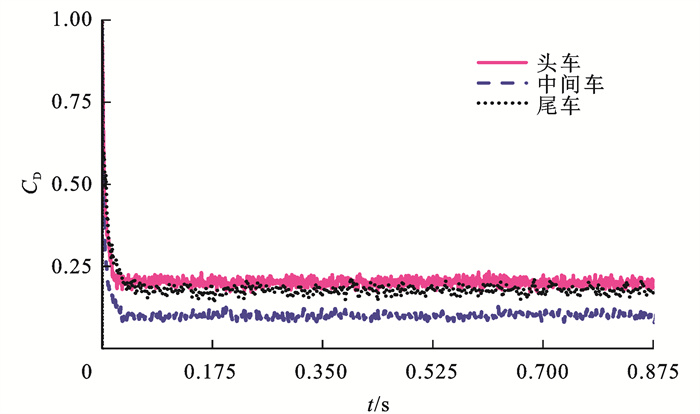
数值计算通过商业软件STAR-CCM+实现。基于隐式非定常可压缩有限体积求解器进行数值模拟，压力速度耦合处理方式采用压力耦合方程组的半隐式算法(Semi-Implicit Method for Pressure Linked Equations, SIMPLE)，对流项采用混合格式进行离散，即在LES区域使用中心有界差分格式，在RANS区域使用二阶迎风格式^[19]。湍流项和扩散项都采用二阶迎风格式，时间步采用二阶隐式格式，每个时间步的最大内迭代次数设置为10，连续方程、动量方程和湍流方程的残差均在1.0×10^-6以下。在瞬态模拟中，时间步长与库朗数C_O有关，其定义为$C_O=U_{\infty} \Delta t / \Delta x \text { ( } \Delta t \text { 为时间步长) }$。为了解析时间尺度较小的湍流结构，并提高全局预测精度，一般要求大部分计算网格区域的库朗数小于1。为了满足这一要求，时间步长Δt设置为6.0×10^-5 s。在该参数设置下，超过99%计算网格的库朗数都是小于1的，先前学者的研究表明^[20]，这种微小差距对流动几乎无显著影响。为了使流场充分发展，2种工况都在计算运行50t^*(参考时间t^*=H/U_∞)后开始记录数据，总的物理时间步长为250t^*，如图 7所示，其中C_D为列车阻力系数，定义为

图  7  原型列车时均阻力系数时间历程曲线

Figure  7.  Time history curves of time-averaged drag coefficients of traditional train

下载: 全尺寸图片 幻灯片

式中：F_D为气动阻力；ρ为空气密度，取1.225 kg·m^-2；S为列车在yOz平面上的投影面积，取0.112 m²。

1.5   数值验证

1.5.1   列车气动阻力

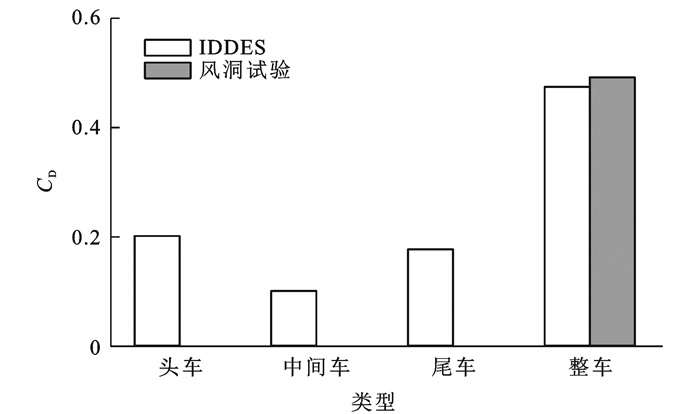
为了验证数值模拟结果的可靠性，将原型高速列车在60 m·s^-1均匀来流下的阻力系数C_D与倪章松^[21]进行的同型号列车风洞试验结果进行对比，如图 8所示。现有研究表明^[22]，在相同边界条件下，当雷诺数大于3.0×10⁵时，流场形态不再发生显著变化。IDDES模拟的雷诺数(2.9×10⁶)和风洞试验的雷诺数(1.9×10⁶)均远大于临界值，因此，可用试验结果验证数值模拟的准确性。

图  8  数值模拟与风洞试验列车时均阻力系数对比

Figure  8.  Comparison of time-averaged drag coefficients of train between numerical simulation and wind tunnel test

下载: 全尺寸图片 幻灯片

由图 8可见，IDDES模型的列车时均阻力系数计算结果略低于风洞试验结果，相差不超过4%。考虑到上述误差在合理范围内，可认为采用的数值方法能准确预测气动力。

1.5.2   流向列车风速度

为了验证当前IDDES模型预测列车风速度的准确性，将原型高速列车流向列车风速度IDDES结果与Sun等^[23]研究的八车编组某型CRH高速列车的DDES结果进行比较，2种方法保持相同的均匀来流速度(350 km·h^-1)，图 9展示了DDES方法的计算域^[23]。

图  9  DDES方法的计算域

Figure  9.  Computational domain of DDES method

下载: 全尺寸图片 幻灯片

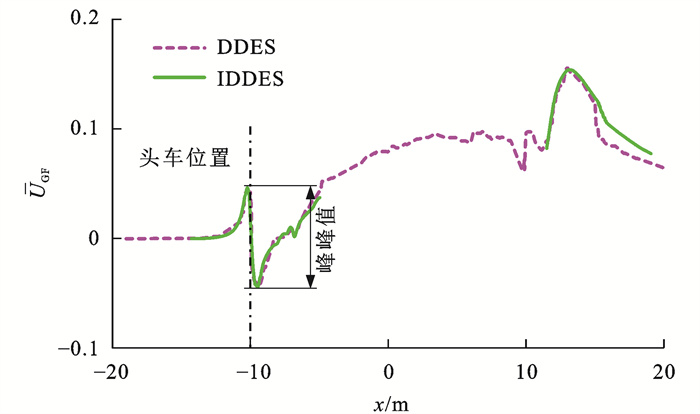
图 10对比了IDDES与DDES结果的时均x向列车风速度$\bar{U}_{\mathrm{GF}}$分布情况，监测线位于轨侧位置(距轨顶0.2 m，距轨道中心3.0 m)，从图 10可看出：IDDES方法可以准确捕捉到头车经过时引起的列车风速度峰值，且与DDES方法的整体趋势几乎一致，但在尾流区，IDDES方法与DDES方法的计算结果出现明显差异，这是由于2种方法的列车尾部网格加密区尺寸有较大不同，同时也和模型编组长度不同有关。

图  10  IDDES和DDES方法的时均流向列车风速度对比

Figure  10.  Comparison of time-averaged streamwise slipstream velocities between IDDES and DDES methods

下载: 全尺寸图片 幻灯片

表 2对比了IDDES方法和DDES得到的头车附近流向列车风速度峰值，可以看到：峰值的差距在10%以内，表明当前的数值计算方法可以准确预测列车风速度。综上，阻力系数、流向列车风速度的总体一致性验证了当前采用IDDES方法的可靠性。

表  2  IDDES和DDES方法的时均流向列车风速度峰值对比

Table  2.  Comparison of peak time-averaged streamwise slipstream velocities between IDDES and DDES methods

模拟方法	正峰值	负峰值	峰峰值
DDES[23]	0.042 2	-0.042 0	0.084 2
IDDES	0.046 4	-0.044 1	0.090 5

下载: 导出CSV 

| 显示表格

2.   结果与讨论

2.1   列车风速度

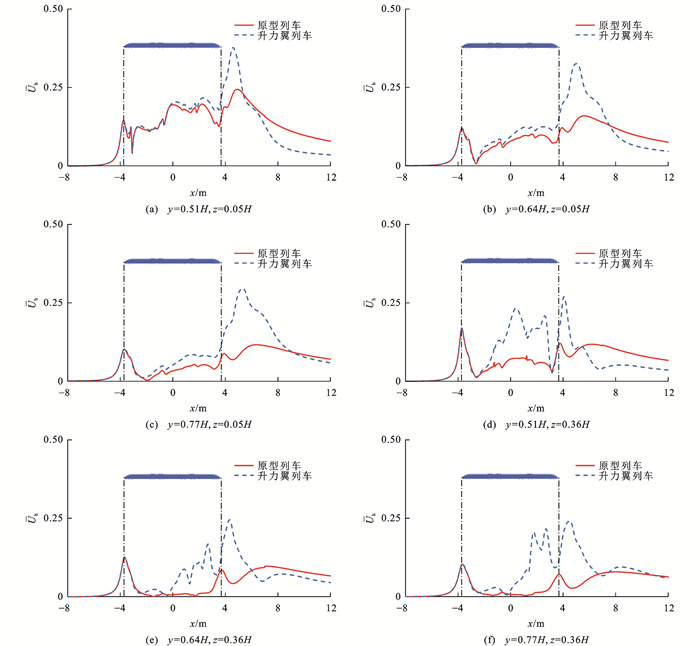
列车高速行驶时，将周围静止空气推向前方，侧面和顶部，形成列车风^[24]。图 11展示了有无升力翼2种工况下距离轨道中心不同位置的时均列车风速度分布情况，可以看出：升力翼对时均列车风速度的影响显著，升力翼列车的最大列车风速度高于原型列车，且其第2个峰值出现位置相对更加滞后；在轨侧高度(z=0.05H)，尾车鼻尖点之前的区域内升力翼列车和原型列车列车风速度曲线整体变化趋势基本一致，从头车顶部第1个升力翼位置开始，升力翼列车时均列车风速度大于原型列车，在近尾迹附近，两者峰值差异尤其明显，但自远离列车尾部的某位置开始，升力翼列车的列车风速度小于原型列车；在站台高度(z=0.36H)，升力翼列车时均列车风速度曲线峰值数明显多于原型列车，在远离列车尾部区域有与在轨道高度处相同的规律，即升力翼列车时均列车风速度衰减得更快。结合图 12中列车周围边界层分布情况，可将该分布规律的原因归结为，由于升力翼的存在，列车上表面不完全平顺，高速气流自翼的边缘产生分离，向外挤压边界层，影响了列车顶部的边界层流动，致使顶面和侧表面边界层厚度的增长率增大，最终累积到尾部区域。

图  11  原型列车和升力翼列车时均列车风速度分布

Figure  11.  Distributions of time-averaged slipstream velocities of traditional train and train with lift airfoils

下载: 全尺寸图片 幻灯片

图  12  原型列车和升力翼列车周围边界层流动

Figure  12.  Boundary layer flows around traditional train

下载: 全尺寸图片 幻灯片

在轨侧位置(y=0.77H，z=0.05H)，与原型列车相比，升力翼列车的最大列车风速度增加了155.6%；在站台位置(y=0.77H，z=0.36H)，升力翼列车的最大列车风速度相对于原型列车提高了132.7%。并且发现，与原型列车不同，升力翼列车的最大列车风速度皆出现在近尾迹区域，这与升力翼列车表面边界层厚度沿纵向增长更快有关^[10]。由此可见，升力翼的增加对轨旁设备和站台人员的安全性有重要影响。

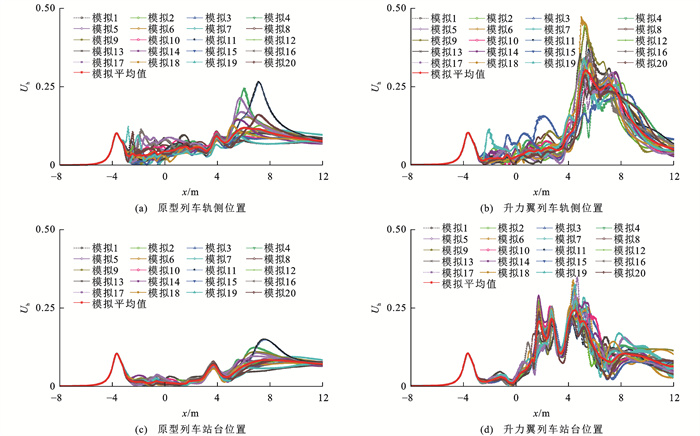
图 13展示了原型列车和升力翼列车在20个独立测点处瞬时列车风速度沿纵向分布情况，根据TSI的规定，速度监测点设置在轨侧和站台位置，沿x方向每隔20 m设置一个测点，每种工况分别进行了20次独立模拟，可以看出：每次模拟结果之间的差异较大，与Flynn等^[20]观察到的现象类似；此外，轨侧瞬时列车风速度整体大于站台位置，原型列车的最大列车风速度出现在头车附近，而升力翼列车则出现在尾迹附近。

图  13  原型列车和升力翼列车瞬时列车风速度

Figure  13.  Instantaneous slipstream velocities of traditional train and train with lift airfoils

下载: 全尺寸图片 幻灯片

2.2   高速列车尾部流场

2.2.1   尾流涡旋结构

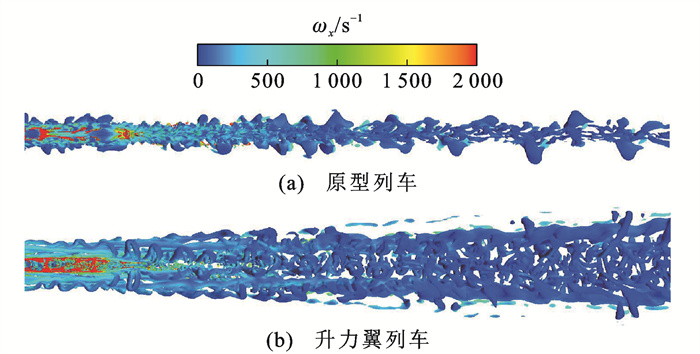
高速列车尾流是非定常和三维的有旋流动，图 14展示了利用Q(速度梯度的第二不变量)准则^[25]识别出的列车尾流涡旋结构，用流向涡量ω_x进行渲染，其中Q的取值用(U_∞/H)²量纲一化，取0.002 7。

图  14  尾流涡旋结构

Figure  14.  Wake vortex structures

下载: 全尺寸图片 幻灯片

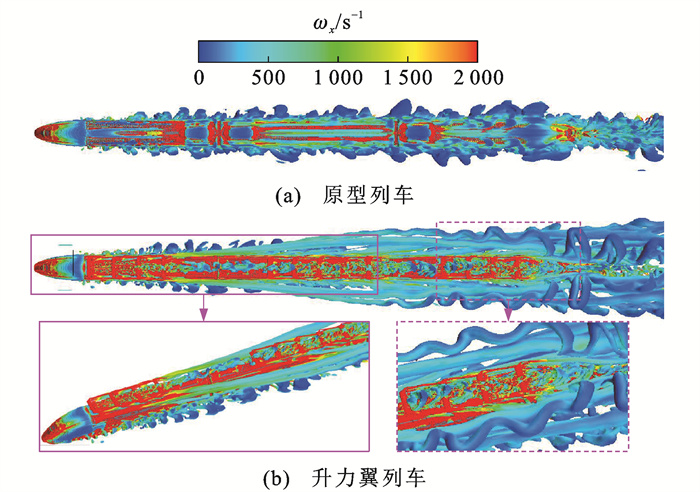
总体来看，尾车附近的涡旋强度较高，随着流向涡对向下游传播，涡强度逐渐衰减，并且由于涡旋彼此之间的诱导及其与地面之间的相互作用，会不断向展向移动。同时，涡旋的拉伸、倾斜和切割变形会引起大尺度涡与地面之间发生不稳定高剪切，致使大尺度涡周围伴随有若干小尺度涡。此外，原型列车和升力翼列车工况下尾涡结构有显著不同，原型列车的尾涡主要由一对反向旋转的流向涡旋组成，而升力翼列车尾迹中出现了2对流向涡旋，即大尺度流向涡对之间夹着一对更为破碎的细小涡旋。Baker^[26]认为，边界层分离及流向的螺旋流动是尾涡结构产生机理的构成要素，因此，可结合图 12中列车尾部的边界层分布，将该现象解释为升力翼加剧了列车表面湍流边界层的流动分离。图 15给出了车身周围涡旋结构分布情况，从中可更清晰地看到尾涡的形成过程：原型高速列车的涡结构沿车身表面较为均匀地向下游发展，而升力翼高速列车的涡结构则表现为从第1个升力翼开始，翼尖尾涡不断向下游和外侧发展，并与下游翼尖涡融合，累积到每节车上最后一个翼的位置形成脱落涡对，最终在尾迹区形成2对流向涡旋。基于此，可以认为升力翼的绕流作用加剧了车身表面湍流边界层的流动分离，使得尾涡结构更加复杂，其中翼尖尾涡对列车尾流结构的形成和发展起主导作用。

图  15  车身周围涡旋结构

Figure  15.  Vortex structures around train body

下载: 全尺寸图片 幻灯片

2.2.2   尾流列车风速度

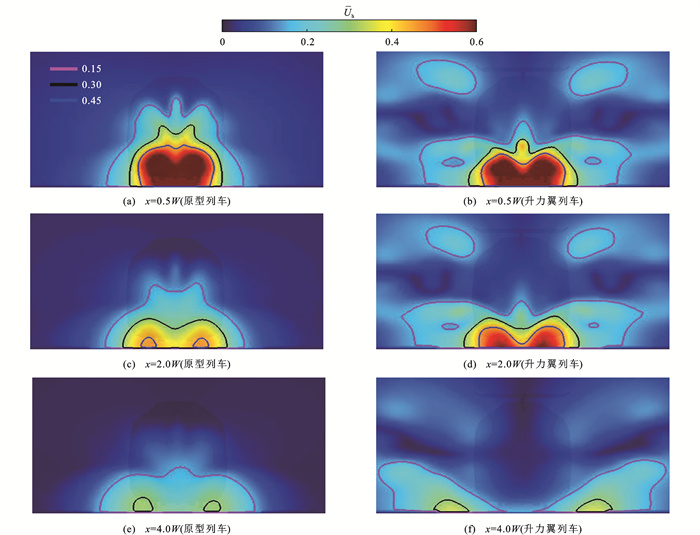
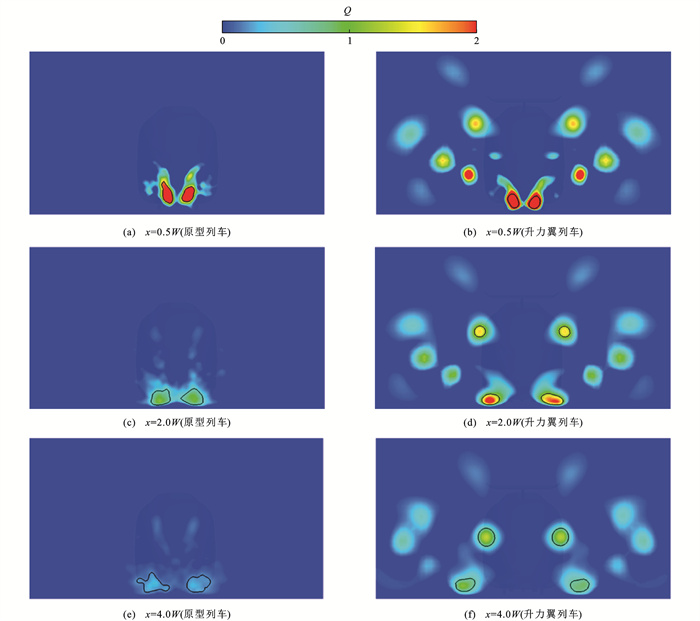
考虑到高速列车尾流区域的涡旋结构会影响列车风的发展^[9]，图 16展示了近尾迹区距尾车鼻部不同距离垂直截面处(x分别为0.5W、2.0W和4.0W)时均列车风速度分布情况，可以看出：越靠近列车尾部，列车风速度越大；升力翼列车在3个垂直截面上的列车风速度等值线分布宽度均大于原型列车，但分布高度较低，表明在近尾迹区，安装升力翼后使列车风速度在展向上有所增大，垂直方向上有所减小，这与图 12中沿车身表面边界层厚度的变化呈现出相似的规律，即在列车尾部，升力翼列车沿纵向的边界层厚度小于原型列车，沿展向则相反；同时，列车车顶两侧区域出现了较高的列车风速度，这可能与升力翼翼尖尾涡脱落有一定关系。

图  16  与尾车鼻尖点不同距离垂直截面的时均列车风速度

Figure  16.  Time-averaged slipstream velocities at vertical planes with different distances from nose tip of tail train

下载: 全尺寸图片 幻灯片

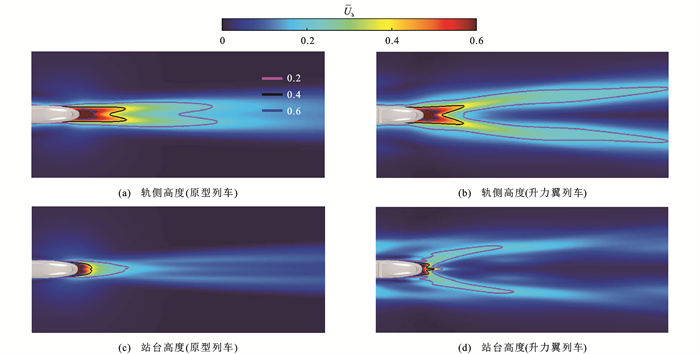
图 17比较了轨侧和站台高度水平面上的时均列车风速度分布情况，可知：与原型列车相比，升力翼列车的时均列车风速度有所增大，并且向展向和流向的延伸范围更大，出现明显的剪切分离；此外，近尾迹区轨侧高度的列车风速度显著高于站台高度。

图  17  轨侧和站台高度水平面的时均列车风速度

Figure  17.  Time-averaged slipstream velocities at horizontal planes of trackside and platform height

下载: 全尺寸图片 幻灯片

一般在尾流中，当Q较大时，可以识别出涡核^[26]。图 18显示了原型列车和升力翼列车距尾车鼻端不同流向距离处Q的时均分布云图，图中实线为等值线$Q=0.5 Q_{\max }\left(Q_{\max } \text { 为 } Q\right. \text { 的最大值) }$，可以看出：不同流向位置的垂直截面上都产生了对称涡，随着流动向下游发展，涡核向下、向外侧移动，涡核强度明显降低，表明涡旋能量在持续耗散；相较原型列车，升力翼列车的涡核位置更加远离尾迹中心，且随着与尾车鼻尖点距离的增加，外移量也逐渐增大，这主要是因为升力翼使列车气动外形沿纵向变化更剧烈，加剧了剪切层的流动分离，导致涡旋脱落位置相较原型列车偏向鼻端外侧；此外，升力翼列车周围有多个涡核强度较大的区域，这与图 14中展现出的复杂尾迹涡旋结构相对应。对比图 16和18可以发现：列车风速度较大的区域与涡核位置十分接近，在沿流向向下游发展的过程中，列车风速度的大值区域与尾流涡旋的移动规律也保持一致。Bell等^[27]指出，具有较高列车风速度的流体从尾迹区中心向外移动与尾迹中的纵向涡有关，本文验证了该观点，列车风速度峰值与尾迹流向涡旋结构确实紧密相关，涡旋强度较大会致使列车风速度较大。

图  18  不同流向位置Q的时均分布

Figure  18.  Time-averaged distributions of Q at different streamwise positions

下载: 全尺寸图片 幻灯片

2.2.3   尾流的频率特征

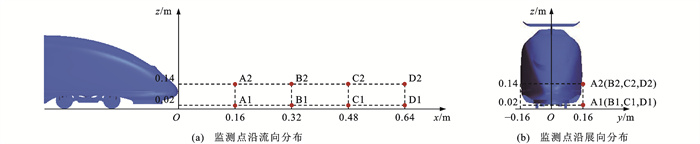
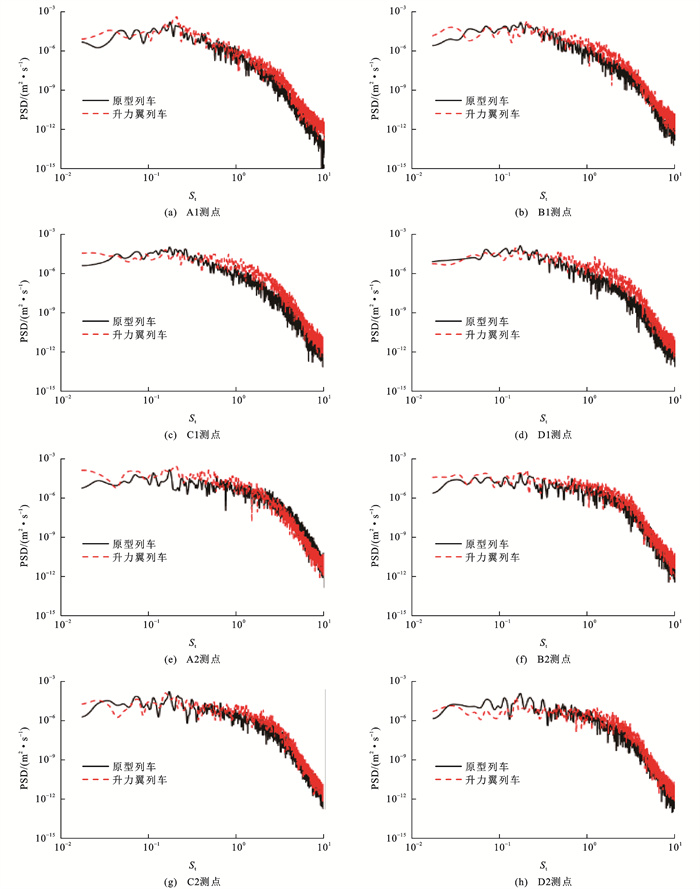
为了探讨尾流的流动机理，进一步分析尾涡结构的瞬态特性。将50t^*~250t^*的数据用于频谱分析，将功率谱密度(Power Spectral Density, PSD)应用MATLAB中的Pwelch函数进行处理，取12个样本序列的平均值^[28]，每个样本序列的周期为57t^*，包含7 000个时间步长，重叠值为50，选择Hamming作为窗函数，以此提高结果的准确性。在尾迹区轨侧和站台高度设置了速度监测点(A1~D1和A2~D2)，如图 19所示。图 20给出尾迹区不同监测点沿x方向瞬时速度的PSD分析结果，2列测点都位于y=0.5W处。将频率f转化成斯特劳哈尔数S_t实现量纲一处理，其中$S_{\mathrm{t}}=f H / U_{\infty}$。

图  19  尾迹区速度监测点

Figure  19.  Velocity monitor points in wake area

下载: 全尺寸图片 幻灯片

图  20  尾迹区不同位置速度监测点的PSD

Figure  20.  PSDs of velocity monitor points at different positions in wake area

下载: 全尺寸图片 幻灯片

观察图 20中尾迹区不同测点处的PSD曲线，可知：尾涡特征频率呈现出宽频特征，原型列车对应的主频的S_t在0.175附近，符合Bell等^[29]的全尺寸试验结果，即尾涡脱落频率在S_t为0.15~0.18的范围内。但升力翼列车的PSD结果与原型列车相比有较大不同，由于其涡结构更加破碎和细小，因而有更高的能量，主频范围与原型列车相比也有所出入。Muld等^[30]认为高速列车边界层发展会对尾涡脱落特征时间尺度产生影响，由图 12可见，升力翼列车的高速气流从翼身周围分离，向外挤压边界层，意味着升力翼的几何外形结构加剧了由车体表面发展出的边界层的流动分离，而这应该是其尾涡脱落频率与原型列车不同的原因。

此外，比较原型列车和升力翼列车尾迹区不同速度测点的PSD曲线斜率可见，升力翼列车尾流展向涡的耗散速度相对较慢，这是因为安装升力翼后，地面效应增强，使得其展向涡在流场中的持续时间更长。综上，可认为升力翼改变了列车尾流区域的振动特性，对尾涡脱落频率和功率谱密度有较大影响。

3.   结语

(1) 安装升力翼后，轨侧和站台位置的列车风速度峰值相对原型列车均有所增大，且第2个峰值出现在较原型列车相对滞后的位置，由此对轨侧设备和站台人员带来的安全性影响更加显著。

(2) 原型列车尾迹由一对反向旋转的流向涡旋主导，而升力翼列车尾迹区形成了2对流向涡旋，其中前后升力翼翼尖涡之间的干扰效应对尾涡结构发展起主导作用。

(3) 升力翼使尾流时均列车风速度在展向分布上增大，垂直分布上减小，水平面上的剪切分离加剧，同时增大了尾涡强度与流向涡对的展向振幅。

(4) 升力翼列车的尾涡结构更加破碎和细小，使得其能量相对原型高速列车有所增大，且由于地面效应，其展向涡在流场中的持续时间更长。

(5) 本文着重于探讨升力翼对列车流场结构的影响效果与程度，发现升力翼在提高升力的同时对列车周围流场产生了一些负面效应，未来会通过优化升力翼参数、调整升力翼布局等方式缓解影响程度，进行更多的优化设计研究。