Optimal configuration and allocation of berth resources in multi-port regions
-
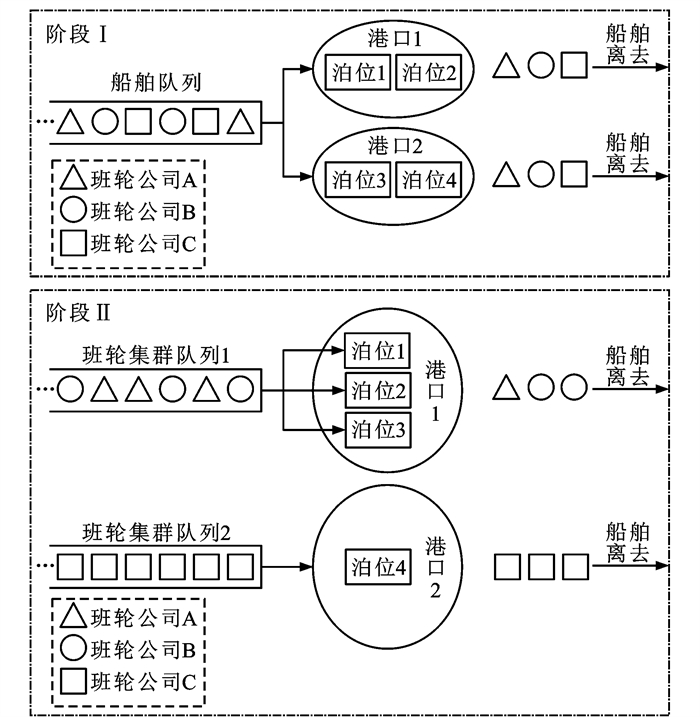
摘要: 在区域港口发展一体化的背景下，通过调整不同班轮公司的船舶挂靠港口，研究了多港口区域泊位资源的配置与分配问题；为提高泊位利用率，将不同班轮公司组合形成稳定班轮集群，并将多港口区域泊位资源与不同班轮集群之间进行最优匹配，以泊位总数最少和船舶挂靠港口调整最小为目标建立集划分模型，设计了基于排队论和合作博弈理论的三阶段优化方法；以珠江三角洲区域的3个港口(香港港、盐田港和蛇口港)和4个班轮公司的船舶挂靠该区域多港口为例进行算例分析。数值分析结果表明：三阶段优化方法可以使这4个班轮公司的船舶总平均排队长度由23.569 1艘减少至22.930 2艘，即多港口区域的泊位资源整合可以有效缓解港口拥挤和船舶排队；3个港口服务4个班轮公司船舶需配置的泊位数由31减少至27，说明多港口区域的泊位资源的合理配置与分配，不仅可以提高泊位资源利用率，也可以减少不同港口的泊位资源的重复建设；从泊位服务船舶数量的角度，服务不同的班轮集群的船舶对港口的吸引力不同，说明港口可以选择合适的班轮公司作为服务对象来提高泊位运营效率。Abstract: Under the background of integrated regional port development, by adjusting berthing ports for the ships from different liner shipping companies, the configuration and allocation of berth resources in multi-port regions were investigated. To improve berth utilization, different liner shipping companies were combined to form stable liner ship clusters and determine the optimal matching between berth resources and different liner ship clusters in multi-port regions. A set partitioning model was established to minimize the number of berths and berthing ports to be adjusted, and a three-stage optimization approach dependent on the queuing theory and cooperative game theory was presented. Three ports (Hong Kong Port, Yantian Port, and Shekou Port) in the Pearl River Delta region, with the ships from four liner shipping companies berthing at the region, were numerically analyzed. Numerical analysis results show that by using the three-stage optimization approach, the average queuing length of the ships from these four liner shipping companies decreases from 23.569 1 to 22.930 2, therefore the integration of berth resources in multi-port regions is helpful in relieving port congestion and ship queuing. The number of berths to be allocated by three ports serving four liner shipping companies reduces from 31 to 27, indicating that the reasonable configuration and allocation of berth resources in multi-port regions can not only improve berth utilization, but also reduce the repetitive construction of port resources of different ports. From the perspective of the number of ships served by berths, the port has different attractiveness when serving the ships of various liner ship clusters, indicating that the port should properly select liner shipping companies for serving their ships in order to improve the operation effectiveness of berth resources.
-
0. 引言
道路交通事故统计资料表明, 道路线形是影响事故发生的重要因素之一[1-3], 道路线形对事故的影响主要体现在纵面线形与平面线形方面[4-5]。相对于纵面线形, 平面线形更加复杂, 这主要是因为其不仅包含圆曲线、直线与缓和曲线, 而且描述平面线形的参数也比较多, 如圆曲线半径、缓和曲线长度、直线长度与平面线形转角等[6-7]。
平面线形是常用的道路线形, 可以调整路线前进的方向, 以适应地形、地物的变化, 但车辆在弯道上行驶时要受到离心力的作用, 弯道离心力的大小又与弯道的半径和车辆的行驶速度有关[8]。如果车速过快, 加上驾驶员的偶尔疏忽、车辆质心偏高与路面条件不好等均可能导致在弯道上行驶的车辆发生危险[9-10]。邹健将重庆市几条主干道的交通事故率与弯道个数的关系绘成散点图, 分析发现单位长度的弯道个数(即弯道密度)与交通事故率有很强的相关关系, 判定系数达到了0.99, 弯道密度增大或减小都会导致事故率上升, 弯道密度随地理环境和道路等级的变化而变化[11]; Vogt等在1991年提出了一个事故预测模型用以预测平面线形上的事故数量, 认为平面线形路段上的事故数量随着曲线长度与曲率的增大而增大, 随着缓和曲线的设置与行车道宽度的增大而减少[12]; Glennon等以理论假设为基础, 利用数据统计分析提出了一个平面线形事故预测模型, 发现平面线形路段的预测事故数是平直路段事故数与曲线特征系数的组合, 与道路曲率与交通量指标成正比[13]; 景天然对道路要素与事故之间的关系进行了研究, 得到了道路平均事故率与平面线形半径的关系[14]; 黄进等收集了湖南某国道的事故数据和线形资料, 对312个圆曲线路段的数据进行拟合, 得到了事故数量与圆曲线长度、曲线角度与缓和曲线长度的关系[15]。
以上这些研究分别以不同平面线形评价指标为研究对象, 分析了路段事故率与平面线形指标之间的关系。然而, 表征平面线形特征的指标众多, 不同指标对事故的影响程度也不同, 采用单一指标研究平面线形与事故率之间的关系, 不能深入挖掘平面线形整体特征与事故率之间的关系, 存在局限性。针对此类问题, 本文通过对实际道路平面线形指标和既往事故数据的采集和分析, 探讨不同路段事故率与角度变化率的关系。
1. 平面线形参数的选择与均值化
在平面线形上, 由地形引起路线的变化体现在路线的方位角上[16-17], 道路曲线偏角的大小表征了路线的弯曲程度。Fitzpatrick等在研究车辆运行速度与平面线形要素的相互关系时, 提出了平面线形安全评价方法[18-19]
式中: R为角度变化率((°)·km-1), 是相似特征路段上每单位长度的角度变化之和; L为路段总长度(m); Q为相似特征连续路段内圆曲线i的长度(m); S为相邻缓和曲线j的长度(m); r为圆曲线i的半径(m)。
由式(1)可知, 角度变化率是路段长度内平均单位长度的偏角变化, 包含了所研究路段内圆曲线长度、圆曲线半径、缓和曲线长度与直线段长度, 并且考虑到了相邻曲线间的相互作用, 反映了平面线形的总体特征。采用式(1)对2条路段的平面线形参数进行计算, 得到事故率y与角度变化率R之间的散点分布, 基于最小二乘法对事故率与角度变化率进行二次多项式拟合, 过程如下[20-23]。
令事故率与角度变化率之间的二次多项式为
式中: a、b、c均为待定系数。
统计所有事故率与角度变化率的数据总数, 记为m, 参考式(2), 误差方程为
式中: α为正整数, 且α∈[1, m];ωα为误差值; yα为统计得到的事故数据; Rα为yα对应的角度变化率。
根据残差平方和最小条件, 求解系数a、b、c的最优解, 并计算拟合精度。然而如果直接采用式(1)~(3)计算事故率与角度变化率的关系, 拟合精度不高, 主要原因在于所选取的样本长度为各个平面线形长度, 而单个样本长度容易受到纵面线形、构造物(桥梁、隧道)等的影响, 为达到平衡和淡化其他因素对事故率的影响, 突出事故率与角度变化率的关系, 本文使用样本均值化方法对角度变化率进行二次处理, 并重新使用最小二乘法进行二次曲线拟合, 过程如下。
Step 1 以0.001 0(°)·km-1为单位对原样本进行划分, 如果某范围内的原样本过多时, 采用0.000 5(°)·km-1为单位进行划分, 划分出n个新样本, 分别为R1、R2、…、Rn。
Step 2 从0.000 1(°)·km-1开始, 分段计算区间内的事故率指标值
式中: yβ为对应角度变化率区间β内的事故率; tγ为β事故数区间第γ个事故数量; p为β区间总的事故数量。
Step 3 为考察相邻路段线形对样本事故率的影响, 本文向前延伸样本长度, 即分别对当前样本路段向前0.25、0.50、0.75、1.00、1.50km的平均事故率与角度变化率之间的关系进行统计分析, 计算方法与式(4)相同。
Step 4 使用最小二乘法对Step 2、3得到的事故率与角度变化率进行二次多项式拟合, 分别得到拟合式与拟合精度。
2. 拟合结果分析
路段1为山岭重丘区二级公路, 双向二车道, 设计行车速度为40km·h-1, 路基宽度为12m, 路段长度为8.8km; 弯多且急, 累计弯道数为22个, 半径小于200m的弯道数为13个, 转角大于100°的弯道数有2个, 弯道密度为2.54个·km-1; 道路一侧为峭壁, 另一侧为深沟, 交通事故频发。在24个月的统计期内, 路段1上共发生事故108起, 造成29人死亡, 110人受伤, 部分事故分布统计数据见表 1。
表 1 路段1平面线形参数与事故分布Table 1. Horizontal alignment parameters and accident distribution of section 1
路段2为二级公路, 路段长度为33.2km; 有一段约长度为9.0km的峡谷地带, 道路坡陡弯急, 沿线地势险要, 分布有5个隧道; 另有一段长度为6.8km的多弯道路段, 分布了29个弯道, 弯道密度为4.26个·km-1, 有一段距离较长的连续的小半径弯道是事故的高发路段。在29个月的统计期内, 该路段共发生事故437起, 造成62人死亡, 242人受伤, 部分事故分布统计数据见表 2。
表 2 路段2平面线形参数与事故分布Table 2. Horizontal alignment parameters and accident distribution of section 2
根据式(4)对所有样本区间进行计算, 依次得到每个平面线形区间内的角度变化率以及当前样本路段向前0.25、0.50、0.75、1.00、1.50km等计算区间(分别计为A、B、C、D、E五个区间)上的平均角度变化率, 部分数据分别见表 3、4。
表 3 路段1事故数量与角度变化率Table 3. Accident mumbers and curvature change rates of section 1
表 4 路段2事故数量与角度变化率Table 4. Accident numbers and curvature change rates of section 2
由表 3、4计算路段1、2区间内的事故率与角度变化率的二次多项式拟合关系, 结果分别见图 1、2。
图 1 路段1事故率与角度变化率的关系Figure 1. Relation between accident rate and curvature change rate of section 1
图 2 路段2事故率与角度变化率的关系Figure 2. Relation between and accident rate curvature change rate of section 2根据表 3中5个计算区间上的事故数量和对应的角度变化率, 得到路段1上5个计算区间的事故率与角度变化率的散点关系, 分别见图 3(a)~7(a), 再进一步均值化处理后, 事故率与平均角度变化率的拟合曲线分别见图 3(b)~7(b)。根据表 4中的5个计算区间事故数量和对应的角度变化率, 得到路段2上事故率与角度变化率的散点关系, 分别见图 8(a)~12(a), 再进一步均值化处理后, 事故率与平均角度变化率的拟合曲线分别见图 8(b)~12(b)。
图 3 路段1中A计算区间上事故率与角度变化率的关系Figure 3. Relations between accident rates and curvature change rates of calculation interval A on section 1
图 4 路段1中B计算区间上事故率与角度变化率的关系Figure 4. Relations between accident rates and curvature change rates of calculation interval B on section 1
图 5 路段1中C计算区间上事故率与角度变化率的关系Figure 5. Relations between accident rates and curvature change rates of calculation interval C on section 1
图 6 路段1中D计算区间上事故率与角度变化率的关系Figure 6. Relations between accident rates and curvature change rates of calculation interval D on section 1
图 7 路段1中E计算区间上事故率与角度变化率的关系Figure 7. Relations between accident rates and curvature change rates of calculation interval E on section 1
图 8 路段2中A计算区间上事故率与角度变化率的关系Figure 8. Relations between accident rates and curvature change rates of calculation interval A on section 2
图 9 路段2中B计算区间上事故率与角度变化率的关系Figure 9. Relations between accident rates and curvature change rates of calculation interval B on section 2
图 10 路段2中C计算区间上事故率与角度变化率的关系Figure 10. Relations between accident rates and curvature change rates of calculation interval C on section 2
图 11 路段2中D计算区间上事故率与角度变化率的关系Figure 11. Relations between accident rates and curvature change rates of calculation interval D on section 2
图 12 路段2中E计算区间上事故率与角度变化率的关系Figure 12. Relations between accident rates and curvature change rates of calculation interval E on section 2运用式(2)、(3)分别计算图 3~12回归方程, 并得到相应的拟合判定系数, 路段1、2拟合结果分别见表 5、6。由图 1、2可知, 路段1、2区间内的拟合结果分别为
对应的判定系数分别为0.414 2与0.120 8, y1、R1与y2、R2分别为路段1与路段2的事故率与角度变化率。
由图 1、3~7可知, 路段1四个计算区间的事故率与角度变化率之间呈现正的二次多项式关系, 但在E计算区间上, 事故率与平均角度变化率之间不呈现该分布规律。在B计算区间上, 该规律最为显著, 以0.001 0(°)·km-1为单位对角度变化率进行重新划分, 对每个区间的样本求平均值得到新样本, 当平均角度变化率为0.002 2(°)·km-1时, 事故率最低。在表 5中, 判定系数也表明当在B计算区间上时, 拟合精度最高, 达到了0.966 1;带下标的y、R、R分别为路段1上相应区间A~E上的事故率、角度变化率与平均角度变化率。
表 5 路段1拟合结果Table 5. Fitting result of section 1
由图 2、8~12可以看出, 路段2四个计算区间上的事故率与角度变化率之间也呈现正的二次抛物线关系, 但在E计算区间上, 事故率与平均角度变化率之间不呈现该分布规律。在B计算区间上, 该规律最显著, 以0.001 0(°)·km-1为单位对角度变化率进行重新划分, 对每个区间的样本求平均值得到新样本, 当平均角度变化率为0.001 8(°)·km-1时, 事故率最低。在表 6中, 判定系数也表明在B计算区间上, 拟合精度最高, 达到了0.790 8;带下标的y、R、R分别为路段2上相应区间A~E上的事故率、角度变化率与平均角度变化率。
表 6 路段2拟合结果Table 6. Fitting result of section 2
由此可见, 路段1、2基本呈现了相同的规律性, 即在B计算区间上, 事故率与平均角度变化率呈现的正二次抛物线关系最为强烈, 当平均角度变化率大约为0.002 0(°)·km-1时, 事故率最低。
3. 结语
(1) 本文选取的2个研究路段均为山区二级公路, 设计行车速度为40km·h-1, 弯道密度较大, 不包含长直线路段。如果研究对象的道路技术等级与设计车速高, 且平面线形更为平缓, 则本文的研究结论可能不适用。
(2) 由于样本量的原因, 本文得到的具体量化值, 适用范围和普遍性受到一定限制, 但用角度变化率表征平面线形特征, 研究平面线形和事故的关系, 反映的曲线特征具整体性。
(3) 在单一曲线内的事故发生不仅受该平面线形的影响, 而且还受到相邻路段线形, 特别是事故发生之前路段线形的影响。
-
表 1 COSCO和MSK组成的班轮集群在港时间分布检验
Table 1. Port time distribution test of liner ship clusters composed of COSCO and MSK
h dh ph nph (dh－nph)2/nph 0~4 1 0.016 2 1.701 0 0.288 9 4~8 14 0.109 8 11.529 0 0.529 6 8~12 21 0.194 6 20.433 0 0.015 7 12~16 25 0.207 6 21.798 0 0.470 4 16~20 17 0.171 5 18.007 5 0.056 4 20~24 7 0.121 5 12.757 5 2.598 4 24~28 7 0.077 8 8.169 0 0.167 3 28~32 2 0.046 3 4.861 5 1.684 3 32~36 6 0.026 1 2.740 5 3.876 8 36~40 2 0.014 1 1.480 5 40~44 2 0.007 3 0.766 5 2.121 4 44~48 1 0.003 7 0.388 5 
下载: 导出CSV
表 2 不同班轮集群的泊松分布和爱尔朗分布的参数
Table 2. Parameters of Poisson distribution and Erlang distribution of different liner ship clusters
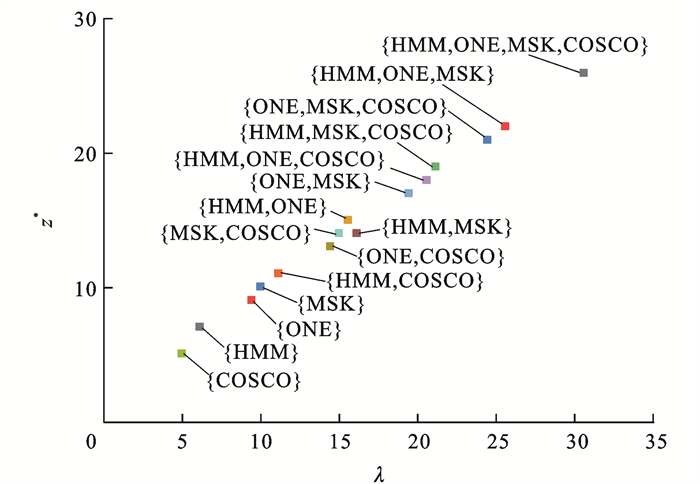
班轮集群 λ k μ {HMM，ONE，MSK，COSCO} 30.57 4 1.409 {HMM，ONE，MSK} 25.57 4 1.405 {ONE，MSK，COSCO} 24.43 3 1.467 {HMM，MSK，COSCO} 21.14 4 1.360 {HMM，ONE，COSCO} 20.57 5 1.398 {HMM，ONE} 15.57 4 1.391 {MSK，COSCO} 15.00 4 1.428 {HMM，MSK} 16.14 4 1.342 {ONE，COSCO} 14.43 5 1.492 {HMM，COSCO} 11.14 5 1.301 {ONE，MSK} 19.43 4 1.479 {HMM} 6.14 3 1.204 {COSCO} 5.00 3 1.424 {ONE} 9.43 6 1.533 {MSK} 10.00 4 1.431
下载: 导出CSV
表 3 最优泊位数结果
Table 3. Results of optimal berth number
班轮集群 z*/个 π(z*)/艘 {HMM, ONE, MSK, COSCO} 26 22.590 1 {HMM, ONE, MSK} 22 19.100 1 {ONE, MSK, COSCO} 21 17.241 5 {HMM, MSK, COSCO} 19 16.415 7 {HMM, ONE, COSCO} 18 15.574 3 {HMM, ONE} 15 12.024 5 {MSK, COSCO} 14 10.942 0 {HMM, MSK} 14 12.844 2 {ONE, COSCO} 13 10.086 0 {HMM, COSCO} 11 9.282 2 {ONE, MSK} 17 13.634 6 {COSCO} 5 4.111 0 {HMM} 7 5.723 1 {ONE} 9 6.428 0 {MSK} 10 7.307 0
下载: 导出CSV
表 4 成本分摊结果
Table 4. Results of cost allocation
班轮集群 每家公司每天分摊的成本/105元 MSK COSCO HMM ONE {HMM, ONE, MSK, COSCO} 6.044 3.246 4.604 5.370 {HMM, ONE, MSK} 6.138 4.591 5.567 {ONE, MSK, COSCO} 6.102 3.232 5.364 {HMM, MSK, COSCO} 5.970 3.442 4.598 {HMM, ONE, COSCO} 3.339 4.598 5.296 {HMM, ONE} 4.641 5.234 {MSK, COSCO} 6.027 3.308 {MSK, HMM} 5.807 4.464 {ONE, COSCO} 3.319 5.289 {HMM, COSCO} 3.279 4.655 {ONE, MSK} 6.189 5.440 不合作 6.237 3.518 4.894 5.488
下载: 导出CSV
表 5 班轮集群稳定性
Table 5. Liner ship clusters stability
案例 班轮集群 每家公司每天分摊的成本/105元 MSK COSCO HMM ONE 1 2家班轮公司 {ONE，MSK} 6.189 5.440 {ONE，COSCO} 3.319 5.289 {MSK，COSCO} 6.027 3.308 3家班轮公司 {ONE，MSK，COSCO} 6.102 3.232 5.364 不参与合作 6.237 3.518 4.894 5.488 2 2家班轮公司 {HMM，ONE} 4.641 5.234 {HMM，MSK} 5.807 4.464 {ONE，MSK} 6.189 5.440 3家班轮公司 {HMM，ONE，MSK} 6.138 4.591 5.567 不参与合作 6.237 3.518 4.894 5.488
下载: 导出CSV
-
[1] GUI Dong-ping, WANG Hai-yan, YU Meng. Risk assessment of port congestion risk during the COVID-19 pandemic[J]. Journal of Marine Science and Engineering, 2022, 10(2): 150. doi: 10.3390/jmse10020150 [2] 王伟, 纪翌佳, 金凤君. 基于动态空间面板模型的中国港口竞争与合作关系研究[J]. 地理研究, 2022, 41(3): 616-632. https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ202203002.htmWANG Wei, JI Yi-jia, JIN Feng-jun. The competition and cooperation relationship of Chinese Ports based on dynamic spatial panel model[J]. Geographical Research, 2022, 41(3): 616-632. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DLYJ202203002.htm [3] 范志强. 连续泊位分配问题研究: 模型优化与计算分析[J]. 工业工程与管理, 2016, 21(3): 81-87. https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201603011.htmFAN Zhi-qiang. Research on continuous berth allocation problem: model comparison and computational analysis[J]. Industrial Engineering and Management, 2016, 21(3): 81-87. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYGC201603011.htm [4] BARBOSA F, BERBERT RAMPAZZO P C, YAMAKAMI A, et al. The use of frontier techniques to identify efficient solutions for the berth allocation problem solved with a hybrid evolutionary algorithm[J]. Computers and Operations Research, 2019, 107: 43-60. doi: 10.1016/j.cor.2019.01.017 [5] URSAVAS E, ZHU S X. Optimal policies for the berth allocation problem under stochastic nature[J]. European Journal of Operational Research, 2016, 255(2): 380-387. doi: 10.1016/j.ejor.2016.04.029 [6] LALLA-RUIZ E, EXPÓSITO-IZQUIERDO C, MELIÁN-BATISTA B, et al. A set-partitioning-based model for the berth allocation problem under time-dependent limitations[J]. European Journal of Operational Research, 2016, 250(3): 1001-1012. doi: 10.1016/j.ejor.2015.10.021 [7] XIANG Xi, LIU Chang-chun, MIAO Li-xin. A bi-objective robust model for berth allocation scheduling under uncertainty[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 106: 294-319. doi: 10.1016/j.tre.2017.07.006 [8] XU Ya, CHEN Qiu-shuang, QUAN Xiong-wen. Robust berth scheduling with uncertain vessel delay and handling time[J]. Annals of Operations Research, 2012, 192(1): 123-140. doi: 10.1007/s10479-010-0820-0 [9] SCHEPLER X, BALEV S, MICHEL S, et al. Global planning in a multi-terminal and multi-modal maritime container port[J]. Transportation Research Part E: Logistics and Transportation Review, 2017, 100: 38-62. doi: 10.1016/j.tre.2016.12.002 [10] IMAI A, NISHIMURA E, PAPADIMITRIOU S. The dynamic berth allocation problem for a container port[J]. Transportation Research Part B: Methodological, 2001, 35(4): 401-417. doi: 10.1016/S0191-2615(99)00057-0 [11] CORRECHER J F, ALVAREZ-VALDES R, TAMARIT J M. New exact methods for the time-invariant berth allocation and quay crane assignment problem[J]. European Journal of Operational Research, 2019, 275(1): 80-92. doi: 10.1016/j.ejor.2018.11.007 [12] ZHENG Jian-feng, YANG Ling-xiao, HAN Wen-cheng, et al. Berth assignment for liner carrier clusters under a cooperative environment[J]. Computers and Operations Research, 2021, 136: 105486. doi: 10.1016/j.cor.2021.105486 [13] ILATI G, SHEIKHOLESLAMI A, HASSANNAYEBI E. A simulation-based optimization approach for integrated port resource allocation problem[J]. PROMET—Traffic and Transportation, 2014, 26(3): 243-255. doi: 10.7307/ptt.v26i3.1337 [14] LEGATO P, MAZZA R M, GULLÌ D. Integrating tactical and operational berth allocation decisions via simulation-optimization[J]. Computers and Industrial Engineering, 2014, 78: 84-94. doi: 10.1016/j.cie.2014.10.003 [15] SAEED N, LARSEN O. Application of queuing methodology to analyze congestion: a case study of the Manila International Container Terminal, Philippines[J]. Case Studies on Transport Policy, 2016, 4(2): 143-149. doi: 10.1016/j.cstp.2016.02.001 [16] EL-NAGGAR M. Application of queuing theory to the container terminal at Alexandria seaport[J]. Journal of Soil Science and Environmental Management, 2010, 1(4): 77-85. [17] DRAGOVI AC'G B, PARK N K, RADMILOVI AC'G Z. Ship-berth link performance evaluation: simulation and analytical approaches[J]. Maritime Policy and Management, 2006, 33(3): 281-299. doi: 10.1080/03088830600783277 [18] KOZAN E. Analysis of the economic effects of alternative investment decisions for seaport systems[J]. Transportation Planning and Technology, 1994, 18(3): 239-248. doi: 10.1080/03081069408717546 [19] SEN P. Optimal priority assignment in queues: application to marine congestion problems[J]. Maritime Policy and Management, 1980, 7(3): 175-184. doi: 10.1080/03088838000000019 [20] EDMOND E D, MAGGS R P. How useful are queue models in port investment decisions for container berths?[J]. Journal of the Operational Research Society, 1978, 29(8): 741-750. doi: 10.1057/jors.1978.162 [21] 张恒, 陈秋双. 考虑船舶废气排放的港口群协同泊位分配研究[J]. 交通运输系统工程与信息, 2014, 14(4): 99-106. https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201404015.htmZHANG Heng, CHEN Qiu-shuang. Coordinated berth allocation for port group considering vessel emissions[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(4): 99-106. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSXT201404015.htm [22] 徐亚, 杜玉泉, 龙磊. 支持多码头协调运作的泊位调度模型和算法[J]. 系统工程, 2015, 33(1): 128-138. https://www.cnki.com.cn/Article/CJFDTOTAL-GCXT201501019.htmXU Ya, DU Yu-quan, LONG Lei. Berth scheduling model and algorithm for coordinated operation of multiple container terminals in a port[J]. Systems Engineering, 2015, 33(1): 128-138. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCXT201501019.htm [23] VENTURINI G, IRIS Ç, KONTOVAS C A, et al. The multi- port berth allocation problem with speed optimization and emission considerations[J]. Transportation Research Part D: Transport and Environment, 2017, 54: 142-159. doi: 10.1016/j.trd.2017.05.002 [24] 毕娅, 李文锋. 集装箱港口集群下多港口多泊位联合调度方法[J]. 计算机应用, 2012, 32(2): 448-451. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201202038.htmBI Ya, LI Wen-feng. Multi-port and multi-berth integrated scheduling based on container port cluster[J]. Journal of Computer Applications, 2012, 32(2): 448-451. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJY201202038.htm [25] GUO Li-ming, ZHENG Jian-feng, DU Hao-ming, et al. The berth assignment and allocation problem considering cooperative liner carriers[J]. Transportation Research Part E: Logistics and Transportation Review, 2022, 164: 102793. doi: 10.1016/j.tre.2022.102793 [26] 梅益群, 韩晓龙. 考虑泊位偏好和岸桥移动的泊位岸桥联合调度[J]. 计算机工程与应用, 2022, 58(6): 241-249. https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG202206024.htmMEI Yi-qun, HAN Xiao-long. Joint scheduling of berths and quay cranes considering berth preference and quay crane movement[J]. Computer Engineering and Applications, 2022, 58(6): 241-249. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSGG202206024.htm [27] 焦小刚, 郑斐峰, 徐寅峰, 等. 考虑泊位疏浚的连续型泊位和动态岸桥联合调度[J]. 运筹与管理, 2020, 29(2): 47-57. https://www.cnki.com.cn/Article/CJFDTOTAL-YCGL202002007.htmJIAO Xiao-gang, ZHENG Fei-feng, XU Yin-feng, et al. Integrated continuous berth allocation and time-variant quay crane assignment under berth dredging in container terminal[J]. Operations Research and Management Science, 2020, 29(2): 47-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YCGL202002007.htm [28] KIMURA T. Approximations for multi-server queues: system interpolations[J]. Queueing Systems, 1994, 17(3): 347-382. [29] 张一诺. 港口通用泊位最佳数量的计算方法[J]. 系统工程理论与实践, 1983(1): 35-41. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL198301009.htmZHANG Yi-nuo. Calculation method of optimal number of port general berths[J]. System Engineering Theory and Practice, 1983(1): 35-41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL198301009.htm -
下载:
点击查看大图
计量
- 文章访问数: 562
- HTML全文浏览量: 315
- PDF下载量: 100
- 被引次数: 0
