Analysis of the Random Vibration Responses Characteristics of the Vehicle-Track Coupling System
-
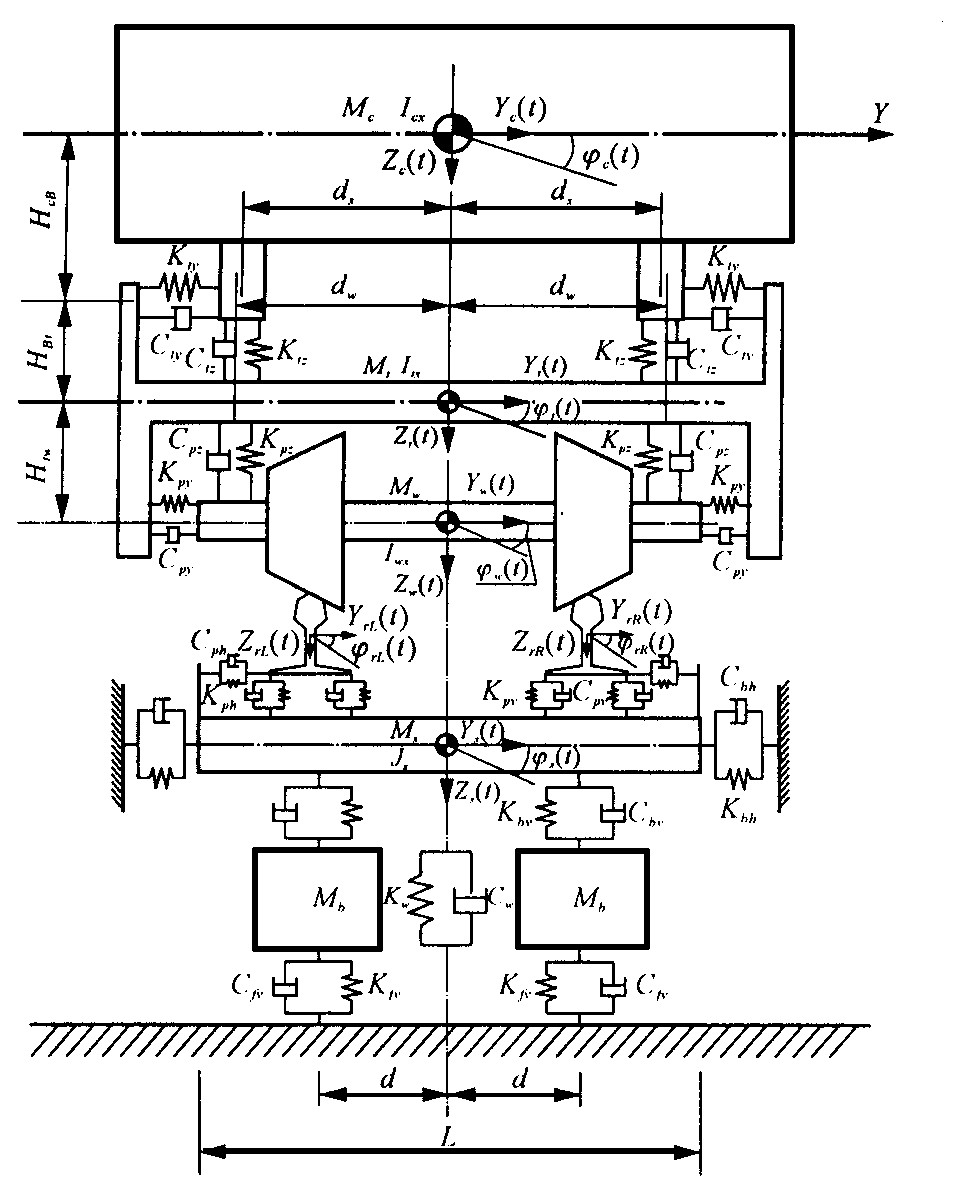
摘要: 基于车辆—轨道耦合动力学理论, 通过建立车辆—轨道垂横耦合模型, 利用时域数值积分法进行了耦合系统的随机响应分析。在此基础上, 采用周期图法估计出车辆—轨道垂向和横向随机响应功率谱密度PSD, 并进行了谱分析。最终得到了车辆—轨道耦合系统随机振动的基本规律Abstract: Based on the theory of vehicle track coupling dynamics, the vertical and lateral coupling model of the vehicle track system is set up.The random vibration responses are carried out through the numerical integration method, and the vertical and the lateral random responses PSD of the vehicle and the track are achieved by the period graph method.Finally the characteristics of the vehicle track system random responses are obtained.
-
Key words:
- vehicle /
- track /
- coupling model /
- random vibration
-
[1] 翟婉明. 车辆-轨道耦合动力学[M]. 北京: 中国铁道出版社, 1997. [2] 陈果. 车辆-轨道耦合系统随机振动分析[D]. 成都: 西南交通大学, 2000. [3] 罗林. 轨道随机干扰函数[J]. 中国铁道科学, 1982, 13(1): 74-110. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK198201007.htm [4] 长沙铁道学院随机振动研究室. 关于机车车辆/轨道系统随机激励函数的研究[J]. 长沙铁道学院学报, 1985, (2): 1-36. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD198502000.htm [5] ZHAI Wan-ming. Two simple fast integration methods for large-scale dynamic problems in engineering [J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 4 199-4 214. [6] 徐昭鑫. 随机振动[M]. 北京: 高等教育出版社, 1990. [7] 王福天. 车辆系统动力学[M]. 北京: 中国铁道出版社, 1981. [8] 王澜. 轨道结构随机振动理论及其在轨道结构减振中的应用[D]. 北京: 铁道部科学研究院, 1988. [9] GRAG V K, DUKKIPATI R V.Dynamics of railway vehicle system [M]. Academic Press, 1984. [10] SHENTON M J. The vibrational environment of the rail, sleeper and ballast[M]. Technical Memorandum. British Rail Research, Derby, 1974. [11] 翟婉明. 铁路轮轨冲击振动模拟与试验[J]. 计算力学学报, 1999, 16(1): 93-99. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG901.013.htm -
下载:
点击查看大图
图(14)
计量
- 文章访问数: 411
- HTML全文浏览量: 96
- PDF下载量: 266
- 被引次数: 0
