Thermal Stress in Two-layer Concrete Slab due to Restraint of Interface
Article Text (Baidu Translation)
-
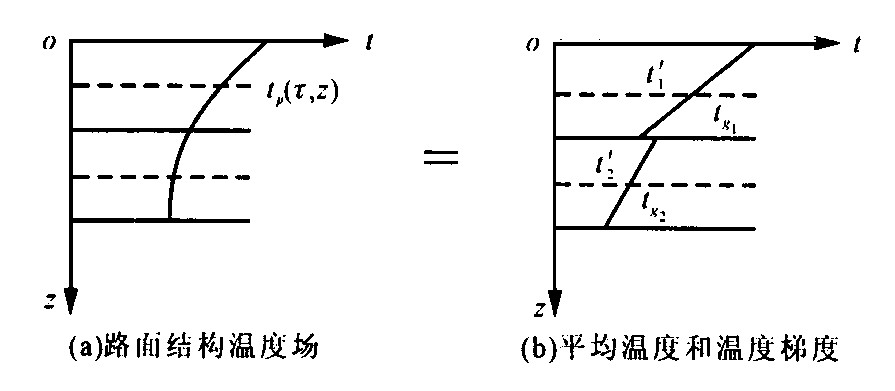
摘要: 分析双层水泥混凝土路面板温度应力构成, 导出不同层间结合状况下由层间变形协调条件引起的层间约束应力的计算通式, 按常用的水泥混凝土路面温度场, 分析板间约束应变的特征, 并给出其计算公式Abstract: Thermal stress in two layer concrete slab is composed of threee parts: (a) inner stress due to nonlinear distribution of temperature in slab section, (b) warping stress due to reaction restraint of foundation, and (c) stress due to restraint strain of interface. An expression is derived for calculating the thermal stress due to restraint strain of interface with different bonding condition, and the characteristic of restraint strain of interface is also analysed and formulated with conventional temperature regime in concrete pavements.
-
Key words:
- concrete pavement /
- two layer slab /
- thermal stress /
- restraint of interface
-
[1] 杨广庆, 刘树山, 刘田明. 高速铁路路基设计与施工[M]. 北京: 中国铁道出版社, 1999. [2] ZHAI Wan-ming. Two simple fast integration methods for large-scale dynamic problems in engineering [J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 4 199-4 214. doi: 10.1002/(SICI)1097-0207(19961230)39:24<4199::AID-NME39>3.0.CO;2-Y [3] 石田诚, 三浦重, 河野昭子. 桥台背部填土沉降引起的轨道变形及车辆运行特性[A]. 轨道结构刚度合理值及其合理匹配的研究资料集[C], 1999. -





 下载:
下载: