Sdudy on Platoon Dispersion Model
-
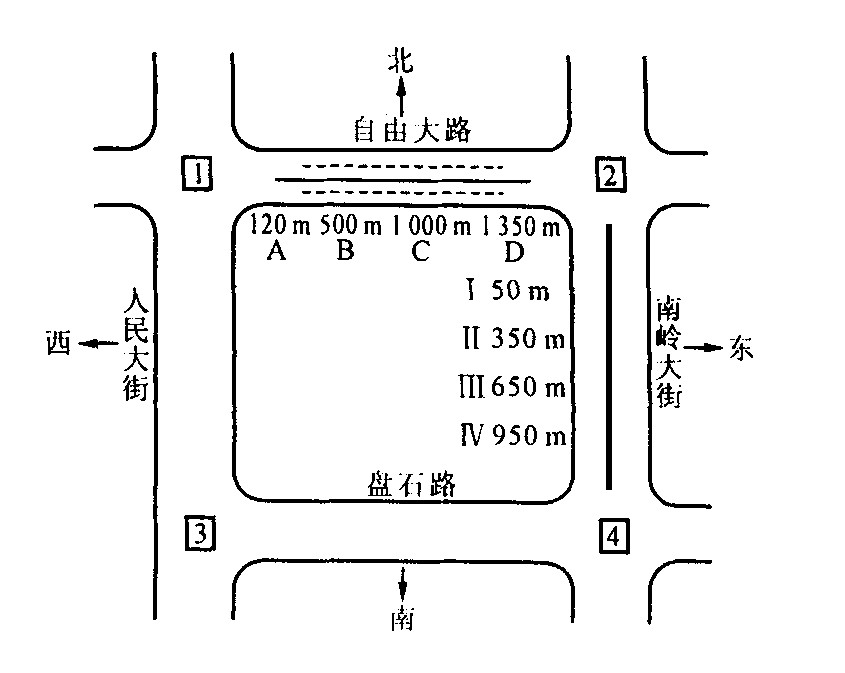
摘要: 用“多点摄像法”对长春市的2个路段交通流进行了实地调查。通过数据处理, 给出了车队离散过程中的多点流量图式以及多段的车速分布。用实际观测数据所得的流量图式与TRRL的流量图式进行对比, 分析异同。还对车辆行驶速度及行驶时间分布进行了拟合, 分析了各离散模型的适用范围。最后对车队离散进行计算机仿真, 得出了满意的结论Abstract: The field research is done to two road links in Changchun city by multi spot photography.After data processing, traffic flow volume figures are given.The contrast of these figures with those of TRRL is provided.The intimation of vehicles' speed distribution and run time distribution is also given, as well as the applicable range of each platoon dispersion model.Simulation model of platoon dispersion is also presented with good results.
-
Key words:
- platoon dispersion /
- volume figure /
- distribution intimation /
- signal timing /
- delay
-
表 1 第一点至第二点的行驶速度(行驶时间) 分布拟合
离散条件 观测数据 速度统计特征 分布特点 车道 距离/m 时间 起迄点 均值 方差 速度 行驶时间 双车道 380 6:15 A—B 9.6189 10.6291 D1 D6 7:30 A—B 8.0916 4.6704 D1 D3 9:00 A—B 11.3473 15.3752 D2 单车道 300 7:40 Ⅰ—Ⅱ 9.5862 3.1964 9:00 Ⅰ—Ⅱ 10.3879 4.3559 D1、D2 
下载: 导出CSV
表 2 第一点至第三点的行驶速度(行驶时间) 分布拟合
离散条件 观测数据 速度统计特征 分布特点 车道 距离/m 时间 起迄点 均值 方差 速度 行驶时间 双车道 880 6:15 A—C 11.5059 10.6425 D3 7:30 A—C 10.0698 3.3683 D1、D2 9:00 A—C 11.0600 6.0435 D1 单车道 600 7:40 Ⅰ—Ⅲ 9.2927 3.0329 9:00 Ⅰ—Ⅲ 10.7260 4.8621 D1、D2
下载: 导出CSV
表 3 第一点至第四点的行驶速度(行驶时间) 分布拟合
离散条件 观测数据 速度统计特征 分布特点 车道 距离/m 时间 起迄点 均值 方差 速度 行驶时间 双车道 1230 6:15 A—D 12.4522 9.8202 D1、D2 7:30 A—D 9.6711 2.5886 D1、D2 9:00 A—D 10.8468 3.7143 D1、D2 单车道 880 7:40 Ⅰ—Ⅳ 9.5889 3.0302 D2 D4 9:00 Ⅰ—Ⅳ 11.2983 5.1393 D1、D2 注: D1-正态分布; D2-对数正态分布; D3-几何分布; D4-泊松分布; D5-二项分布; D6-负二项分布。
下载: 导出CSV
表 4 车队离散及排队仿真结果(车队按方式1产生)
离散模型 平均延误/s 平均队长/veh 最大延误/s 最大队长/veh 1 18.50 2.39 50 15 2 17.86 2.34 50 14 3 18.51 2.34 50 14 4 18.20 2.43 50 14 5 18.28 2.48 50 16 6 18.28 2.42 50 15
下载: 导出CSV
表 5 车队离散及排队仿真结果(车队按方式2产生)
离散模型 平均延误/s 平均队长/veh 最大延误/s 最大队长/veh 1 24.16 7.88 50 28.00 2 24.54 8.03 50 28.17 3 24.58 8.08 50 31.00 4 24.33 7.98 50 29.80 5 24.31 7.95 50 30.00 6 24.32 8.06 50 30.00
下载: 导出CSV
表 6 车队离散及排队仿真结果(车队按方式3产生)
离散模型 平均延误/s 平均队长/veh 最大延误/s 最大队长/veh 1 22.22 6.42 50 23 2 23.48 7.32 50 24 3 23.10 7.20 50 25 4 23.43 7.30 50 25 5 23.54 7.24 50 25 6 23.57 7.36 50 25
下载: 导出CSV
-
[1] 全永. 城市交通控制[M]. 北京: 人民交通出版社, 1989. [2] 丹尼尔L, 马休J. 交通流理论[M]. 北京: 人民交通出版社, 1983. -
点击查看大图
图(5) / 表(6)
计量
- 文章访问数: 310
- HTML全文浏览量: 122
- PDF下载量: 316
- 被引次数: 0
