由路段交通量推算OD出行量方法研究——基于多路径概率分配模型的迭代反推法

留言板

尊敬的读者、作者、审稿人, 关于本刊的投稿、审稿、编辑和出版的任何问题, 您可以本页添加留言。我们将尽快给您答复。谢谢您的支持!

姓名

邮箱

手机号码

标题

留言内容

验证码

基金项目:

国家973重点基础研究发展项目 G1998030419

A Study on Estimating OD Trips From Observed Link Flows——Based on the Method of Iterative Procedure to Calculate OD on the Multi-path Assignment Model

Department of Road and Traffic Engineering, Tongji University, Shanghai 200092, China

Article Text (Baidu Translation)

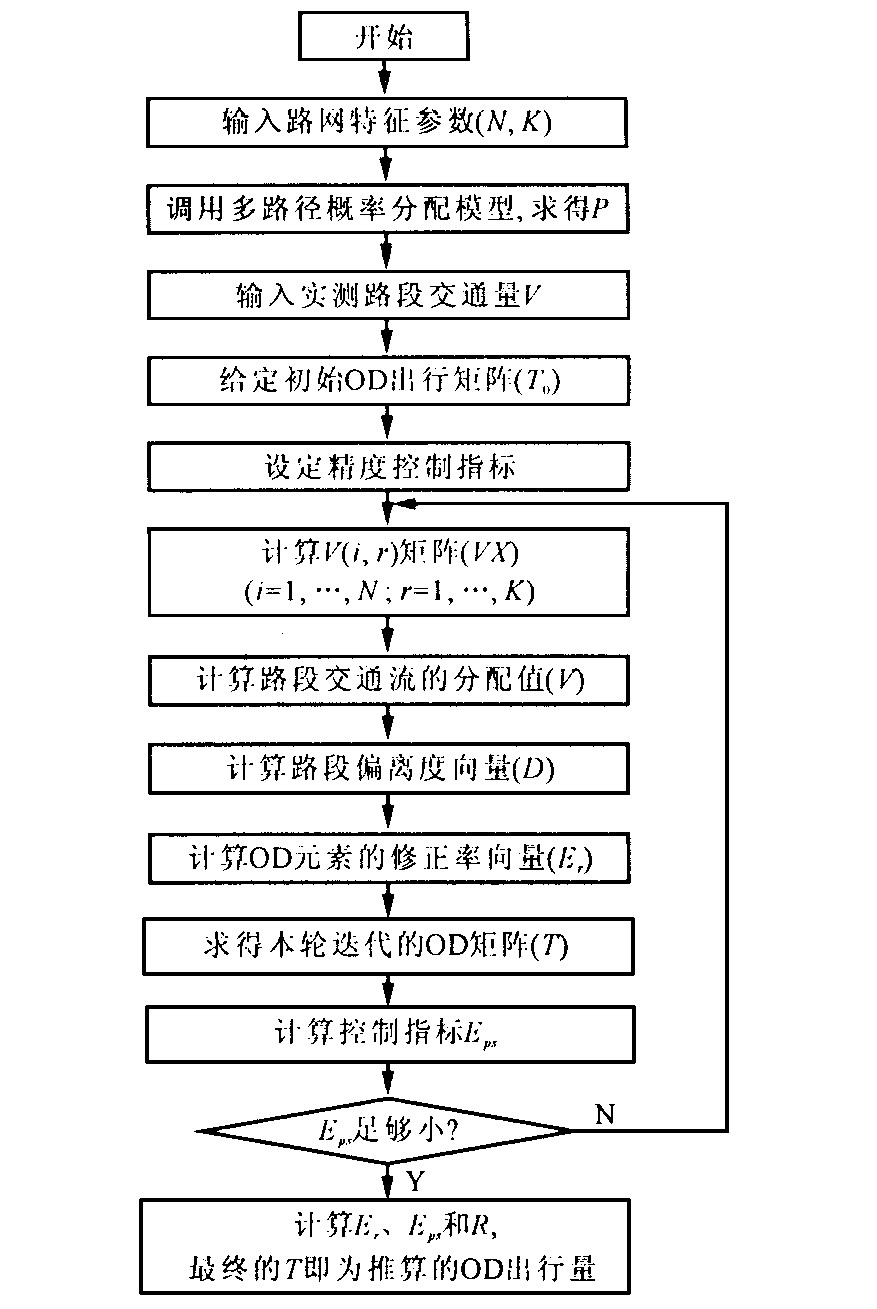
摘要: 在改进有效路段和有效路径定义的基础上, 采用随机—最短路多路径分配模型, 求解分配率矩阵, 建立了多路径分配模型的迭代反推方法, 并采用假设论证法检验了方法系统的可靠性、合理性。讨论了影响出行量推算结果的主要因素, 获得了因变于分配率矩阵的两个重要结论
- 多路径分配模型 /
- 分配率矩阵 /
- 迭代反推 /
- 假设论证法
Abstract: A new iteration framework of estimating OD trips is established by a stochastic shortest path multi path assignment model to calculate the probability matrix P based on the two improved definitions of effective path and effective link.Meanwhile a hypothesis argumentation is put forward to examine the feasibility and rationality of the iteration method.Then the factors of influencing result of estimation are discussed.Finally two important conclusions resulted from P are obtained.
- multi path assignment model /
- probability matrix /
- iterative procedure /
- hypothesis argumentation

[1]	王炜, 等. 城市交通规划理论及其应用[M]. 南京: 东南大学出版社, 1998.
[2]	李景. 由路段交通量推算OD出行量的实用方法研究[D]. 长沙: 长沙交通学院, 1999.