Economic Analysis of Transportation Demand
Article Text (Baidu Translation)
-
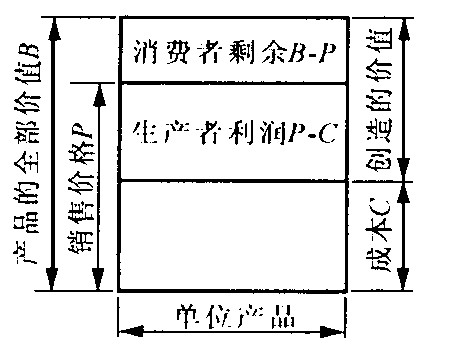
摘要: 在阐述消费者剩余理论的基础上 , 提出运输供给的品质与价格应定位在需求方能够得到一定利益的前提下 , 为此建立了运输需求经济成本计量模型 , 并定性分析了该模型的构成要素对用户经济成本的影响。分析表明 , 运输价格对供需双方的影响并不对称 , 不宜以价格为主要因子来分析供需平衡规律 ;运输对象价值越高 , 运输过程消耗对运输经济成本影响越小。
-
关键词:
- 运输需求分配经济机理 /
- 消费者剩余 /
- 运输需求经济成本
Abstract: On the basis of consumer surplus theory, the idea that transportation supply quality and price should be decided on the premise of demanders' benefits is put forward. Hence, a measurement model for transportation demand economic cost is established, and qualitative analysis for the structural factors of the model and its influent as on the consumers' economic cost is conducted. The analysis shows that the actual influence of transportation price on both suppliers and demanders is dissymmetrical. Because of this, it is not good to analyze the supply-demand balance laws from the view point of prices. The fact is that the higher the value of transportation goods, the smaller the influence on transportation economic cost in its transporting process. -
表 1 日本货物周转次数统计
年度 每周运货次数 1 2 3 4 5 6 7以上 合计 平均 昭和59年 16.4 38.6 19.7 4.9 5.6 14.1 0.8 100% 2.9 昭和62年 4.9 28.6 26.1 9.0 11.3 16.4 3.8 100% 3.7 -
[1] [美]戴维·贝赞可,等.公路战略经济学[M].北京:北京大学出版社,1999. [2] 沈志云.交通运输工程学[M].北京:人民交通出版社,1999. [3] 吴群琪.论我国综合运输网络体系发展的协调问题[A]. 中国交通研究与探索[C].北京:中国铁道出版社,1997. [4] 李天民.现代管理会计学[M].上海:立信会计出版社,1995. [5] 周伟,王选仓.道路经济与管理[M].北京:人民交通出版社,1998. -





 下载:
下载: