Gravity model for partitioning port hinterlands based on fuzzy comprehensive evaluation
Article Text (Baidu Translation)
-
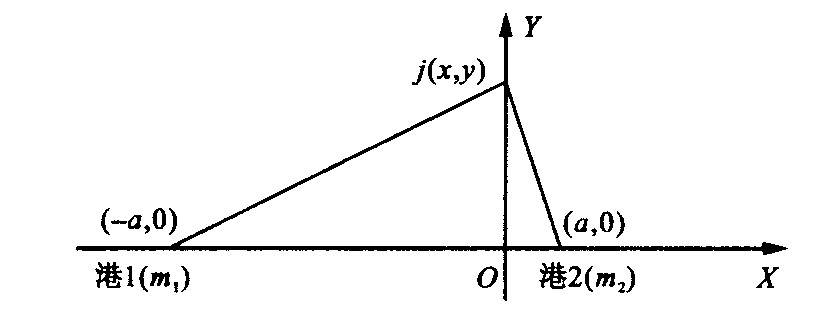
摘要: 现代港口功能的进一步多元化 , 使得影响港口腹地划分因素也趋多样化。为提高划分现代港口腹地范围的科学性和合理性 , 采用引力模型与模糊 ( Fuzzy) 综合评判模型相结合的方法来确定港口对腹地的吸引力及其服务范围 , 并结合实际算例对模型的应用进行了分析 , 为合理划分现代港口腹地 , 提高港口发展规划制定的科学化水平提供了理论指导。Abstract: With the continuing multivariation of port functions, the factors affecting the partition of port hinterlands are also diversifying.In order to improve the scientificalness and rationality of partitioning port hinterlands, this paper adopts a combined approach of the gravity model and fuzzy comprehensive evaluation model to determine the attractive power and service areas of port, and examines the application of the approach through a calculational example.The paper provides a theory guide for rational partitioning of port hinterlands and scientific drawing up of port development plan.
-
Key words:
- port /
- hinterland /
- gravity model /
- fuzzy comprehensive evaluation
-
图 1 港口腹地吸引范围计算示意图
Figure 1. The demonstration figure for computation of port hinterland
表 1 港口腹地吸引力计算
Table 1. Computation for the gravity of port hinterland
因素集 港口A 港口B 港口C u1 0.75 0.45 0.38 u2 0.60 0.05 0.12 u3 0.32 0.40 0.35 u4 0.78 0.10 0.16 u5 0.15 0.06 0.10 u6 0.24 0.38 0.40 
下载: 导出CSV
-
[1] 尚清.港口规划[M].大连:大连海事大学出版社,1998. [2] 韩立岩,汪培庄.应用模糊数学(修订版)[M].北京:首都经济贸易大学出版社,1998.148—151. -
点击查看大图
图(1) / 表(1)
计量
- 文章访问数: 318
- HTML全文浏览量: 136
- PDF下载量: 171
- 被引次数: 0
