-
摘要: 列车运行速度的提高和载重量的增加使其主要承载部件转向架构架的运行环境变得恶劣。为减小轮轨间的作用力, 要对构架进行轻量化设计, 由此引起了构架疲劳强度问题。对某高速列车构架的疲劳试验结果表明, 在给定的常规载荷作用下构架裂纹扩展速度出现延迟效应, 最终减小到零。应用弹塑性裂纹扩展与闭合概念和残余应力松弛概念分析了构架裂纹扩展延迟效应, 结果表明引起构架裂纹扩展速度减慢的主要因素是循环加载中残余应力的松弛, 而裂纹的闭合对裂纹的延迟也有重要影响; 计算了给定工艺构架状态和循环载荷下, 不扩展裂纹初始长度的最小值。Abstract: With the enhancement of the speed and the load capacity of rail vehicles, the running conditions of bogie frame and the main supporting parts of rail vehicle become worse.In order to reduce the interaction force between rail and wheel, the weight of the frame has to be optimized.Thus the fatigue strength of the bogie is of concern.The fatigue experimental results of a high speed train show that the crack propagation of the frame slow down under the cyclic loads.The concept of relaxation of residual stress under cyclic loads and open and close of crack are utilized to analyze the effects of crack propagation.The analysis shows that the main reason of the crack propagation slow down of the frame is the relaxation of the residual stress under the cyclic loads.Crack close also affects the crack growth greatly.The maximum allowable length of non propagation crack is calculated under the given configuration and cyclic loads.
-
Key words:
- bogie frame /
- residual stresses /
- crack propagation /
- frame fatigue
-
图 3 点5、7、8处裂纹扩展与载荷频数的关系
Figure 3. Relationship of crack length vs. load cycles in point 5、7、8
图 4 测试点5处残余应力随n变化关系
Figure 4. Relationship of residual stress with load cycle number in point 5
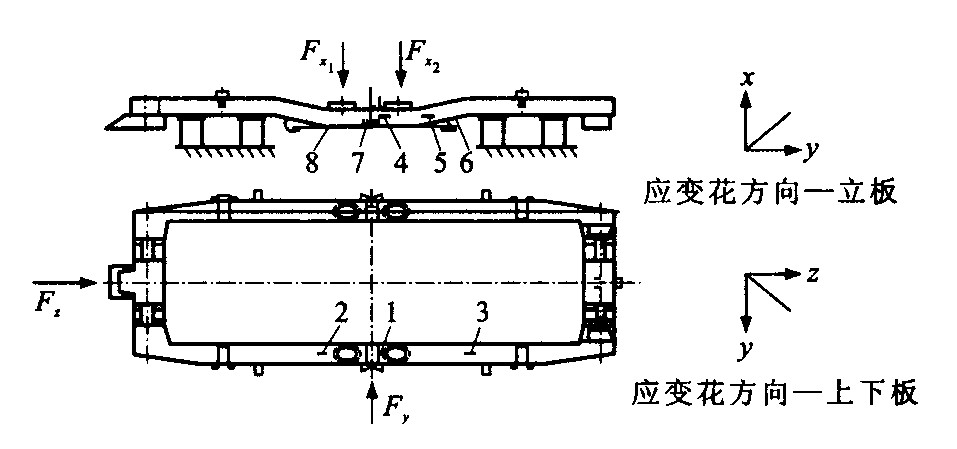
表 1 疲劳试验载荷
Table 1. Fatigue test loads
载荷方向 载荷值 波形 频率/Hz Fx1=Fx2 300±60 kN sine 4 Fy 10±30 kN sine 4 Fz ±100 kN square Change direction in 5 minutes 
下载: 导出CSV
表 2 测点最大、最小等效应力
Table 2. Maximum and minimum equivalent stress in test points
应力 测点 4 5 7 8 σmax/MPa 83 102 113 101 σmin/MPa -30 -15 10 8
下载: 导出CSV
-
[1] Tanaka K, Hoshide T, Yamada A, Taira S. Fatigue crack propagation in biaxial stress fields[J]. Fatigue Engng Mater. Struct., 1979, 2(2): 181-194. [2] Kitagawa H, Yuki R, Tohgo K. A fracture mechanics approach to high-cycle fatigue crack growth under in plane biaxial loads[J]. Fatigue Engng Mater. Struct., 1979, 2(2): 195-206. [3] Lam Y C. Fatigue crack growth under biaxial loading [J]. Fatigue fract Engng Mater. Struct., 1993, 16(4): 429-440. [4] Radaj D. Design and Analysis of Fatigue Resistant Welded Structures[M]. London: Woodhead Publishing Ltd, 1990. [5] 徐灏. 疲劳强度[M]. 北京: 高等教育出版社, 1998. [6] 高庆. 断裂力学[M]. 重庆: 重庆大学出版社, 1986. [7] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1993. -
点击查看大图
计量
- 文章访问数: 246
- HTML全文浏览量: 82
- PDF下载量: 285
- 被引次数: 0
