Simulation of collection and allocation of empty containers based on Petri net
Article Text (Baidu Translation)
-
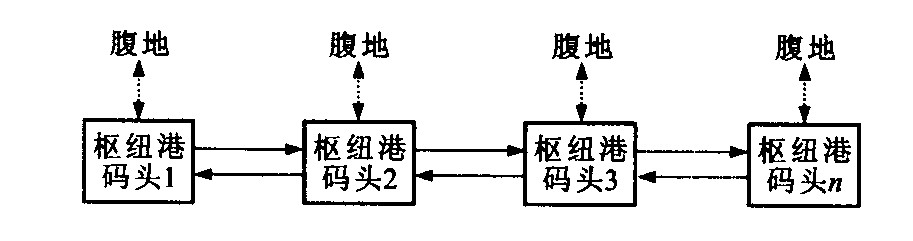
摘要: Petri网可以很方便地用来分析离散事件系统和建立模型。对集装箱空箱调运系统(CAECS) 进行了分析, 构建空箱调运的Petri网模型, 然后利用EXSPECT仿真软件进行模拟仿真, 从而证明了利用Petri网分析和解决集装箱空箱调运问题的有效性。Abstract: Petri net can be conveniently utilized to analyze DES and to build its model.This paper analyzes the CAECS (System of Collection and Allocation of Empty Containers), builds its Petri net model, and then simulates the model by simulation software EXSPECT so as to testify the effectiveness of Petri net.
-
Key words:
- Petri net /
- CAEC /
- simulation
-
-
[1] LIU Heng-jiang. The analysis of collection and allocation of empty containers[J]. Containerization, 2001, (10): 11-13. [2] 袁崇义.Petri网原理[M]. 北京: 电子工业出版社, 1998. [3] SHI Xin. The simulation and optimization of the shipping business process based on Petri net[J]. Journal of System Simulation, 2001, 13(6): 767-780. [4] 蒋正雄, 刘鼎铭. 集装箱运输学[M]. 北京: 人民交通出版社, 1997. [5] Teoor Gabriel Crainic, Michel Gendreau, Pierre Dejax. Dynamic and stochastic models for the allocation of empty containers[J]. Journal of the Operational Research Society, 1992, (10): 102-126. -





 下载:
下载: