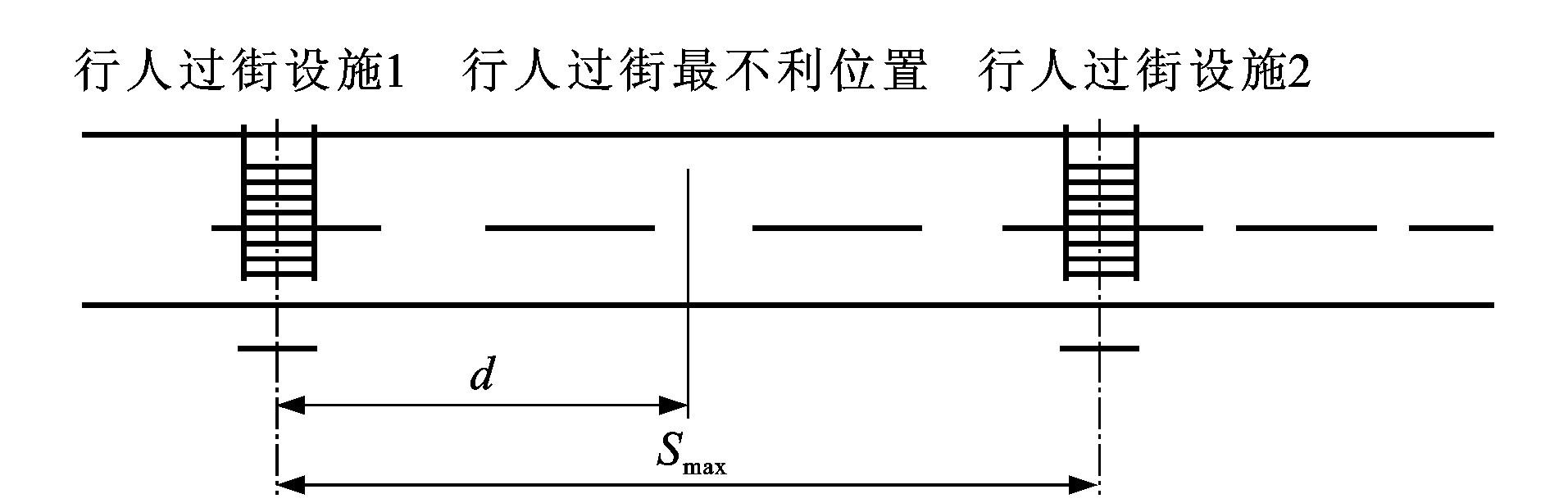
Reasonable distance of pedestrian crossing facilities
Article Text (Baidu Translation)
-
摘要: 行人交通是城市交通的重要组成部分。在行人交通特性分析基础上, 通过对行人心理、车辆行驶、道路通行能力等分析, 提出了平面行人过街设施合理间距的分析计算方法。根据中国城市交通的一般情况, 分别对城市中心商业区和城市一般地区的行人过街设施合理间隔进行计算, 提出了相应的行人过街设施合理间隔的推荐值Abstract: Pedestrian transportation is a key part of urban transportation.On the basis of pedestrian flow characteristics, through the analysis of pedestrian psychology, vehide driving and street capacity, the method of setting the distance of pedestrian crossing facilities can be decided. The paper calculates the reasonable distance of pedestrian crossing facilities in urban central business district and normal district. The recommend values of the corresponding pedestrian crossing facilities distance are put forward.
-
Key words:
- pedestrian /
- traffic characteristics /
- crossing facilities /
- distance
-
[1] 王炜, 过秀成. 交通工程学[M]. 南京: 东南大学出版社, 2000. [2] 中国公路学会《交通工程手册》编委会. 交通工程手册[M]. 北京: 人民交通出版社, 1998. [3] 杨佩昆, 张树升. 交通管理与控制[M]. 北京: 人民交通出版社, 1995. [4] LIN Si-neng. Traffic simulation at pedestrian's crossing[J]. Journal of Guangdong Institute of Technology, 1996, 13(4): 107-112. [5] 王炜, 徐吉谦. 城市交通规划理论及其应用[M]. 南京: 东南大学出版社, 1998. -





 下载:
下载: