Influence of track parameter on welded turnout combination system
-
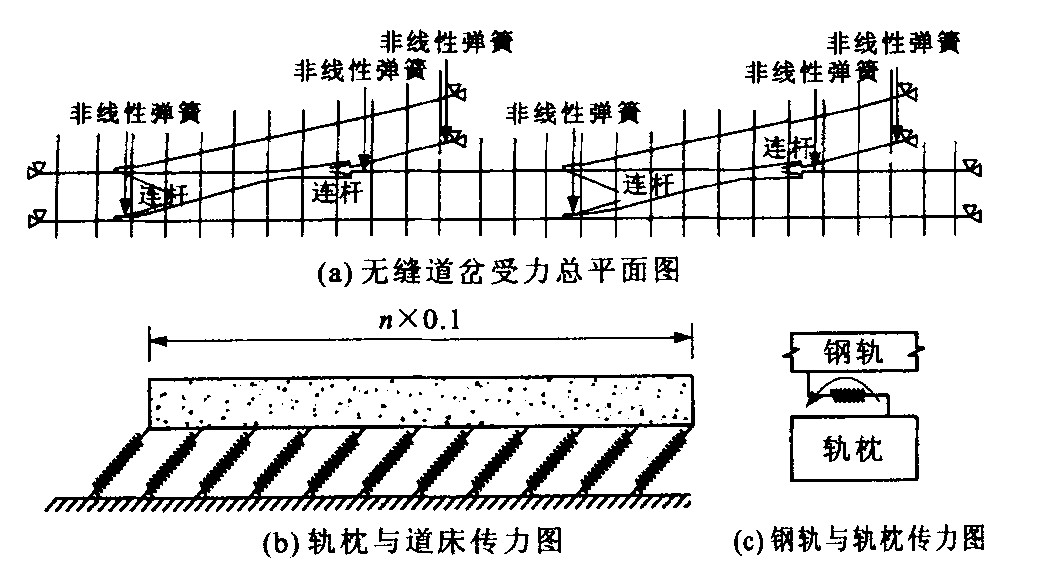
摘要: 基于有限单元法, 建立了组合无缝道岔钢轨纵向力及位移的力学计算模型, 编制了计算软件, 并以1 2号固定辙叉无缝道岔为例, 分析了不同轨道参数对组合无缝道岔钢轨附加力及位移的影响, 并与其对单组无缝道岔的影响作了对比分析。研究表明, 道床纵向阻力对组合无缝道岔钢轨附加力及位移的影响要明显大于单组无缝道岔, 扣件阻力和限位器间隔对组合道岔和单组道岔的影响差不多, 扣件阻力对组合道岔的影响略大于单组道岔, 而限位器间隔对组合道岔的影响略小于单组道岔, 相比单组无缝道岔, 保持组合道岔道床质量显得更为重要。Abstract: A mechanical model and its software based on the finite element principle were presented, the additional longitudinal force and displacement of the welded turnout combination system were discussed. With an example, the influences of track parameters on rail displacement and longitudinal force of the combination system and single welded turnout were calculated, and the results were analyzed.The results show that the ballast resistance has a stronger influence on the welded turnout combination system than that of the single welded turnout, the influence of fastener resistance and the gap limit of spacer pieces is almost the same; the fastener resistance has a little more but the gap limit of spacer pieces has a little less influence on the welded turnout combination system than that of the single welded turnout.
-
表 1 不同道床纵向阻力对应计算结果
Table 1. Results comparison of difference ballast longitudinal resistance
项目 道床极限纵向阻力/N·cm-1 20 25 32 40 50 单组道岔 最大钢轨附加力/kN 312.6 304.1 294.2 286.2 274.6 辙跟位移/mm 7.11 5.90 4.72 3.74 2.98 最大钢轨位移/mm 7.11 5.90 4.72 3.74 2.98 限位器剪力/kN 288.084 291.555 297.763 307.13 317.716 组合道岔 最大钢轨附加力/kN 426.7 406.9 357.9 313.2 286.1 左道岔辙跟位移/mm 11.62 8.28 6.41 4.22 3.11 最大钢轨位移/mm 12.25 8.77 6.61 4.33 3.18 左道岔限位器剪力/kN 270.41 284.02 291.41 307.8 319.7 表 2 不同扣件纵向阻力对应计算结果
Table 2. Results comparison of difference fastener longitudinal resistance
项目 扣件极限纵向阻力/kN·组-1 6 9 12 15 18 单组道岔 最大钢轨附加力/kN 293.90 294.05 294.21 295.08 295.22 辙跟位移/mm 4.68 4.72 4.72 4.70 4.73 最大钢轨位移/mm 4.68 4.72 4.72 4.78 4.88 限位器剪力/kN 448.56 362.07 359.30 241.41 192.76 组合道岔 最大钢轨附加力/kN 345.20 357.20 357.90 358.50 359.30 左道岔辙跟位移/mm 5.77 6.30 6.31 6.35 6.42 最大钢轨位移/mm 5.86 6.59 6.61 6.66 6.94 左道岔限位器剪力/kN 455.25 357.69 291.41 245.72 186.68 表 3 不同夹直线长度对应计算结果
Table 3. Results comparison of difference distance between the turnouts
项目 夹直线长度/m 0 10 25 40 55 70 ∞ 组合道岔 最大钢轨附加力/kN 408.36 388.22 357.9 328.8 307.1 299.6 294.21 左道岔辙跟位移/mm 8.00 7.35 6.41 5.58 5.06 4.86 4.72 最大钢轨位移/mm 8.51 7.71 6.61 5.69 5.06 4.86 4.72 左道岔限位器剪力/kN 286.14 286.99 291.41 297.4 299.3 298.97 297.8 表 4 不同限位器间隙对应计算结果
Table 4. Results comparison of difference spacer gap
项目 限位器间隙/mm 3 5 7 9 13 单组道岔 最大钢轨附加力/kN 340.18 317.53 294.21 270.51 222.18 辙跟位移/mm 6.00 5.36 4.72 4.05 2.97 最大钢轨位移/mm 6.00 5.36 4.72 4.15 3.33 限位器剪力/kN 467.99 373.64 297.76 230.12 112.60 组合道岔 最大钢轨附加力/kN 410.74 384.94 357.86 329.92 272.08 左道岔辙跟位移/mm 8.19 7.29 6.41 5.57 4.03 最大钢轨位移/mm 8.26 7.37 6.61 5.95 4.83 左道岔限位器剪力/kN 454.30 364.29 291.41 226.93 115.58 -
[1] 广钟岩. 铁路无缝线路[M]. 北京: 中国铁道出版社, 2001. [2] 蔡成标, 翟婉明, 王其昌. 无缝提速道岔钢轨温度力与位移计算[J]. 西南交通大学学报, 1997, 32(5): 513—517. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT705.008.htmCAI Cheng-biao, ZHAI Wan-m ing, WANG Qi-chang. Temperature force and displacement in welded switches ofspeed-raising railways[J]. Journal of Southwest Jiaotong University, 1997, 32(5): 513—517. (inChinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT705.008.htm [3] 蔡成标, 王其昌. 30号无缝道岔钢轨温度力与位移计算分析[J]. 铁道学报, 1999, 21(4): 51—54. doi: 10.3321/j.issn:1001-8360.1999.04.013CAI Cheng-biao, WANG Qi-chang. Analysis of railtemperature stress and displacement of welded switch 30[J]. Journal of the China Railway Society, 1999, 21(4): 51—54. (inChinese). doi: 10.3321/j.issn:1001-8360.1999.04.013 [4] 王平, 黄时寿. 可动心轨无缝道岔的非线性计算理论研究[J]. 中国铁道科学, 2001, 22(1): 84—91. doi: 10.3321/j.issn:1001-4632.2001.01.013WANG Ping, HUANG Shi-shou. Study on the nonlineartheory of welded turnout with movable-point frog[J]. ChinaRailway Science, 2001, 22(1): 84—91. (inChinese). doi: 10.3321/j.issn:1001-4632.2001.01.013 [5] 马战国. 秦沈客运专线38号无缝道岔纵向力分析与实验研究[J]. 中国铁道科学, 2002, 23(2): 71—74. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200202012.htmMA Zhan-guo. The analysis and research of longitudinal forceofNo. 38turnout connected withCWR rails onQin-shenrailway[J]. ChinaRailwayScience, 2002, 23(2): 71—74. (inChinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200202012.htm [6] 范俊杰, 谷爱军, 陈岳源. 无缝道岔的理论与实验研究[J]. 铁道学报, 2000, 22(2): 55—59. doi: 10.3321/j.issn:1001-8360.2000.02.013FAN Jun-jie, GU Ai-jun, CHEN Yue-yuan. Theoreticalcalculation and testing analysis for continuous welded turnouts[J]. Journal of the China Railway Society, 2000, 22(2): 55—59. (inChinese). doi: 10.3321/j.issn:1001-8360.2000.02.013 [7] 王平. 无缝道岔群对钢轨位移和纵向力的影响研究[J]. 铁道学报, 2002, 24(2): 74—78. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200202018.htmWANG Ping. Study on influences of welded turnout group on displacements and longitudinal forces of rails[J]. Journal of the China Railway Society, 2002, 24(2): 74—78. (inChinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200202018.htm [8] 李秋义, 陈秀方. 无缝道岔组合效应的研究[J]. 铁道学报, 2002, 24(5): 84—88. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200205018.htmLI Qiu-yi, CHEN Xiu-fang. Analysis of working effect of welded turnout combination system[J]. Journal of the China Railway Society, 2002, 24(5): 84—88. (inChinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200205018.htm -





 下载:
下载: