Three-dimensional vehicle dynamics model for road traffic accident simulation and reconstruction
Article Text (Baidu Translation)
-
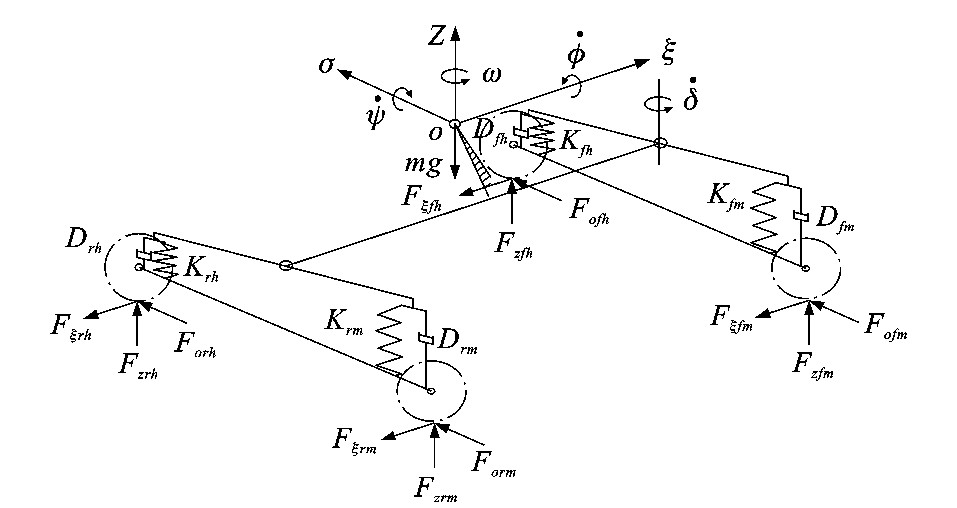
摘要: 应用动力学理论, 提出了用于道路交通事故模拟再现分析的车辆动力学三维模型, 并引用日本汽车研究所的16例车对车实车碰撞实验数据对该三维模拟模型的计算误差进行界定, 并与二维四轮模拟模型的计算精度进行了定量比较, 针对实际道路交通事故案例进行了模拟再现。实例证明车辆三维模型在计算车辆碰撞动力学问题时的总体平均相对误差值为6.65%, 虽然相对于车辆二维四轮模型其速度计算精度在总体水平上降低了1.43%, 但若考虑到其对道路交通事故形态的包容性和形象化方面的优势, 计算精度的适度降低是可以接受的。Abstract: With dynamics theory, a 3-D vehicle dynamics model for road traffic accident simulation and reconstruction was put forward. Through refering to 16 car-to-car impact test datum, the computation error of the 3-D simulation model was defined, and the computation precisions of the 3-D vehicle model and 2-D four-wheel model were compared in quantity. The results of simulation and reconstruction for real traffic accidents show that the general average relative error of the 3-D vehicle model used to compute such the intensive motion as the vehicle impact is 6.65%, and the computation precision of the 3-D model decreases by 1.43% than that of the 2-D model, the proper reduction of computation precision is acceptable because of its advantage in the area of traffic accident type accommodation and visualization.
-
图 3 三维模型与二维四轮模型平均相对计算误差比较
Figure 3. Comparison of average relative computation errors between 3-D and 2-D simulation models
图 4 三维模型道路交通事故模拟再现
Figure 4. Simulation and reconstruction for traffic accident of 3-D model
表 1 计算车速与实测车速比较
Table 1. Comparison of computation vehicle speeds and measured vehicle speeds
下载: 导出CSV
-
[1] 魏朗, 刘浩学. 汽车安全技术概论[M]. 北京: 人民交通出版社, 1998. [2] 魏朗, 石川博敏. 冲突事故再现の解析モデルに关门すゐ研究[J]. 自动车研究, 1995, 17(10): 23-26. [3] 魏朗, 陈荫三, 中辶十隆, 等. 车对车碰撞事故再现计算机模拟系统的研究[J]. 中国公路学报, 1996, 9(4): 105-110. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL604.019.htmWEI Lang, CHEN Yinsan, Takashi Nakatsuji. A study of computer simulation system for reconstructing car-to-car collisions traffic accidents[J]. China Journal of Highway and Transport, 1996, 9(4): 105-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL604.019.htm [4] Gwanghun Gim, Parviz E Nikravesh. An analytical model of pneumatic tyres for vehicle dynamic simulations, part 2: comprehensive slips[J]. Int. J. of Vehicle Design, 1991, 12(1): 23-27. [5] Gwanghun Gim, Parviz E Nikravesh. An analytical model of pneumatic tyres forvehicle dynamic simulations, part 3: validation against experimental data[J]. Int. J. of Vehicle Design, 1991, 12(2): 170-176. [6] 魏朗. 用于碰撞事故中车辆动力学模拟的轮胎模型分析[J]. 西安公路交通大学学报, 1999, 19(1): 73-76. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL902.020.htmWEI Lang. An analysis of vehicle dynamic simulating tire model used in collisions accidents[J]. Journal of Xi'an Highway University, 1999, 19(1): 73-76. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL902.020.htm [7] 魏朗. 车辆碰撞事故解析计算中主要影响因素的误差界定[J]. 中国公路学报, 2000, 13(1): 109-113. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200001025.htmWEI Lang. Establishment of error bounds for the main effect factor in car-to-car collision model[J]. China Journal of Highway and Transport, 2000, 13(1): 109-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200001025.htm -
点击查看大图
图(4) / 表(1)
计量
- 文章访问数: 347
- HTML全文浏览量: 152
- PDF下载量: 223
- 被引次数: 0
