压实石灰黄土力学特性试验

张洪亮; 胡长顺; 刘保健; 王建海

压实石灰黄土力学特性试验

1.
长安大学公路学院, 陕西西安 710064
2.
南阳市公路局, 河南南阳 473003

详细信息

作者简介:
张洪亮(1974-), 男, 山东枣庄人, 讲师, 博士研究生, 从事道路与铁道工程研究

中图分类号: U412.221
计量
- 文章访问数: 273
- HTML全文浏览量: 88
- PDF下载量: 161
- 被引次数: 0
出版历程
- 收稿日期: 2003-01-03
- 刊出日期: 2003-04-25

Mechanical properties experiment of compacted loess-lime

1.
School of Highway, Chang'an University, Xi'an 710064, China
2.
Highway Bureau of Nanyang City, Nanyang 473003, China

More Information

Author Bio:
ZHANG Hong-liang(1974-), male, doctoral student, 86-29-82335826, zhlzhl218@yahoo.com.cn

摘要

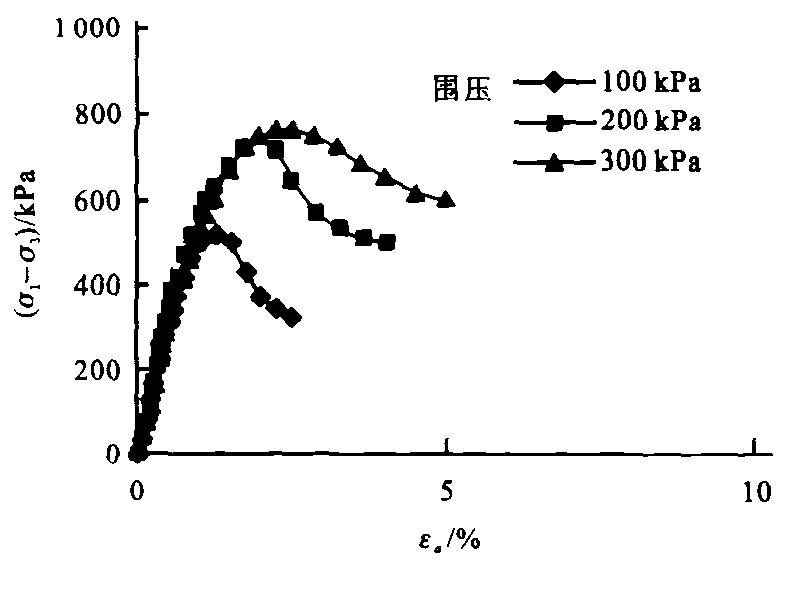
摘要: 通过对公路上广泛使用的灰土比为10%(重量比)、压实度为95%的压实石灰黄土进行三轴试验, 测得了不同围压下压实石灰黄土的应力-应变曲线、体积变形曲线及侧向变形曲线, 获得了压实石灰黄土的初始切线模量、初始切线体积模量、初始泊松比、峰值强度、峰值应变、残余强度和抗剪强度参数等力学指标。结果分析证明邓肯-张模型不适用于压实石灰黄土, 可以使用改进的Saenz公式来表示其应力-应变关系。
- 道路工程 /
- 压实石灰黄土 /
- 三轴试验 /
- 应力-应变曲线 /
- 邓肯-张模型 /
- 改进的Saenz公式
Abstract: Based on the triaxial test of compacted loess-lime, whose rate of lime weighs to soil is 10%, compactness is 95%, the paper measured the stress and strain relationship curve, volume change curve and lateral change curve of the compacted loess-lime under different surrounding pressure, got the parameters of compacted loess-lime, such as elastic modulus, initiative volume modulus, initiative poission's ratio, peak strength, peak strain, residual strength, etc. Analysis results indicate Duncan-change model does not adopt to the compacted loess-lime, the modified Saenz formula can be used as the constitution equation very well.
- road engineering /
- compacted loess-lime /
- triaxial test /
- stress and strain relationship curve /
- Duncan-change model /
- modified Saenz formula

HTML全文

图 1 (σ₁-σ₃)-ε_a关系曲线

Figure 1. (σ₁-σ₃)-ε_a curve

下载: 全尺寸图片幻灯片

图 2 初始压密阶段(σ₁-σ₃)-ε_a关系曲线

Figure 2. (σ₁-σ₃)-ε_a curve of initial compression phase

下载: 全尺寸图片幻灯片

图 3 (σ₁-σ₃)-ε_v关系曲线

Figure 3. (σ₁-σ₃)-ε_v curves

下载: 全尺寸图片幻灯片

图 4 围压600 kPa时(σ₁-σ₃)ε_v关系曲线

Figure 4. (σ₁-σ₃)-ε_v curves under 600 kPa surrounding pressure

下载: 全尺寸图片幻灯片

图 5 ε_a-ε_r关系曲线

Figure 5. ε_a-ε_r curves

下载: 全尺寸图片幻灯片

图 6 初始压密阶段ε_a-ε_r关系曲线

Figure 6. ε_a-ε_r curves of initial compression phase

下载: 全尺寸图片幻灯片

图 7 压实石灰黄土抗剪强度曲线

Figure 7. Shear strength curves of compacted loess-lime

下载: 全尺寸图片幻灯片

图 8 压实石灰黄土三轴应力-应变曲线

Figure 8. (σ₁-σ₃)-ε_a curves of compacted loess-lime

下载: 全尺寸图片幻灯片

表 1 试验用黄土主要物理指标

Table 1. Physics indices of loess

下载: 导出CSV

表 2 不同围压条件下的强度

Table 2. Strength parameters under the different surrounding pressure

下载: 导出CSV

参考文献(9)

[1]	张登良. 加固土原理[M]. 北京: 人民交通出版社, 1990.
[2]	罗强, 蔡英. 成都粘土石灰土的试验研究[J]. 西南交通大学学报, 1996, 31(1): 42-47. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT601.006.htm LUO Qiang, CAI Ying. Experimental study on the lime-soil of Chengdu clay[J]. Journal of Southwest Jiaotong University, 1996, 31(1): 42-47. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT601.006.htm
[3]	张军丽, 刘保健. 水泥黄土的力学特性试验研究[J]. 西安公路交通大学学报, 1999, 19(2): 6-9. https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL902.002.htm ZHANG Jun-li, LIU Bao-jian. The experiment research on the characteristics of cement loess[J], Journal of Xi'an Highway University, 1999, 19(2): 6-9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAGL902.002.htm
[4]	钱家欢, 殷宗泽. 土工原理与计算[M], 北京: 中国水利水电出版社, 2000.
[5]	熊冰, 胡定. 河砂石灰三合土单轴压缩全应力应变曲线的试验与分析[A]. 第三届全国青年岩土力学与工程会议论文集[C]. 南京: 河海大学出版社, 1998.
[6]	江见鲸, 冯乃谦. 混凝土力学[M]. 北京: 中国铁道出版社, 1991.
[7]	黄鹤, 张俐, 杨晓强. 水泥土材料力学性能的试验研究[J]. 太原理工大学学报, 2000, 31(6): 705-709. doi: 10.3969/j.issn.1007-9432.2000.06.028 HUANG He, ZHANG Li, YANG Xiao-qiang. Experiment study of mechanical properties of cemented-soil[J]. Journal of Taiyuan University of Technology, 2000, 31(6): 705-709. (in Chinese) doi: 10.3969/j.issn.1007-9432.2000.06.028
[8]	董毓利, 谢和平, 李世平. 混凝土受压损伤力学本构模型的研究[J]. 工程力学, 1996, 13(1): 44-53. DONG Yu-li, XIE He-ping, LI Shi-ping. Continuum damage mechanics constitutive model of concrete under compression[J]. Engineering Mechanics, 1996, 13 (1): 44-53. (in Chinese)
[9]	万玉珍, 林德明. 重塑黄土的应力应变关系[J]. 岩土工程学报, 1996, 18(6): 106-110. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC606.015.htm WAN Yu-zhen, LIN De-ming. The stress and strain relation-ship of remolded loess[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(6): 106-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC606.015.htm