城市道路中的通道控制模型

基金项目: 上海市教委重点科研基金项目

Traffic corridor control model of urban road

Department of Road and Traffic Engineering, Tongji University, Shanghai 200092, China

Article Text (Baidu Translation)

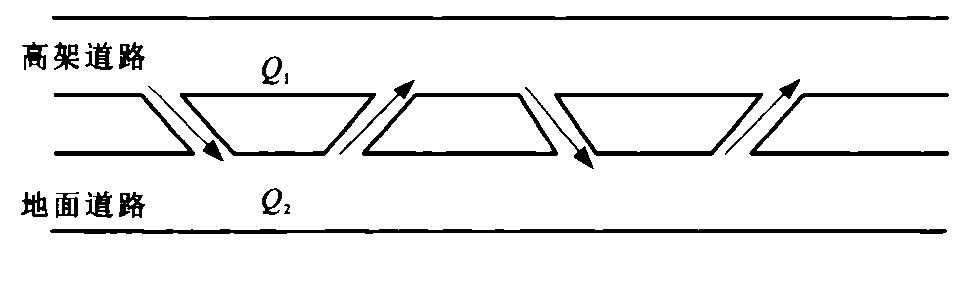
摘要: 将高速公路中通道控制的概念应用于城市道路, 研究了这种控制模式在城市中的应用范围, 讨论了通道控制策略, 采用总行程时间作为控制变量, 分别推导了总行程时间的各组成部分, 并建立总行程时间最小控制策略下的通道控制数学模型和控制流程。数值算例结果表明: 采用总行程时间最小为控制策略的城市交通通道控制方法, 可使系统达到最佳。
- 交通工程 /
- 通道控制 /
- 控制模型 /
- 总行程时间
Abstract: The corridor control model, which is usually used in freeway, was adopted to urban road control. Its applying situation and control strategy were analyzed when the total travel time was taken as control parameter. The constitute parts of total travel time were seperated. The minimization of total travel time as a control goal, its mathematical model and control program were developed. With an example, the results show that this control technology is an effective way to make the control system optimum,
- traffic engineering /
- corridor control /
- control model /
- total travel time

图 1 高架道路与地面道路

Figure 1. Elevated road and ground road

下载: 全尺寸图片幻灯片

图 2 模型的控制流程

Figure 2. Flow chart of control model

下载: 全尺寸图片幻灯片

图 3 算例路段

Figure 3. Example segment

下载: 全尺寸图片幻灯片

表 1 控制参数及计算结果

Table 1. Control parameters and control results

下载: 导出CSV

[1]	刘伟铭, 杨兆升. 高速公路系统控制方法[M]. 北京: 人民交通出版社, 1998.
[2]	杨佩昆, 张树生. 交通管理与控制[M]. 北京: 人民交通出版社, 1995.
[3]	李海渊, 秦吉玛, 王彦卿. 交通控制手册[M]. 北京: 人民交通出版社, 1987.
[4]	Markos Papageorgiou. An integrated control approach for traf-fic corridors[J]. Transpn. Res. C, 1995, 3(1): 19-29.
[5]	Tanner, J C. A Theoretical Analysis of Delays at an Uncon-trolled Intersection. [M]. Springer-Verlag Publications, 1975.
[6]	Ajay K Rathi. A control scheme for high traffic density sectors[J]. Transpn. Res. B, 1988, 22(1): 81-101.
[7]	Kimber R M. Traffic Queues and Delays at Road Junctions[M]. TRRL LR. 909, 1979.
[8]	Newman L A, Dunnet G. Freeway ramp control-what it canand cannot do[J]. Traffic Engineering, 1969, 19(7): 14-21.