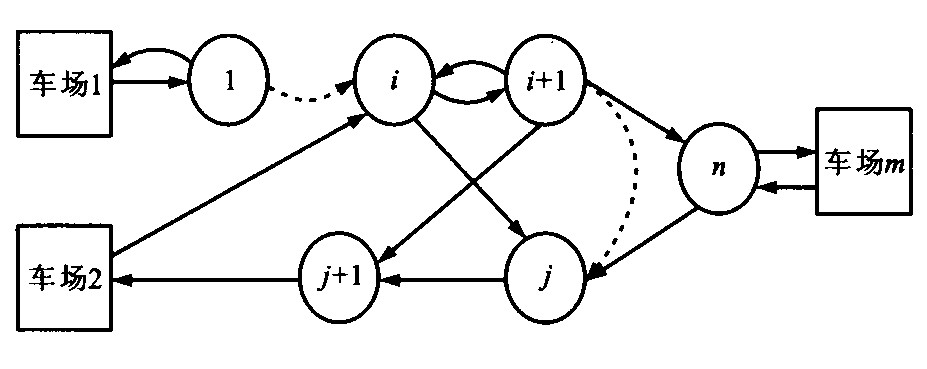
Model and algorithm of multiple depot transit vehicle scheduling
Article Text (Baidu Translation)
-
摘要: 针对多车场满载运输问题的特征, 提出了多车场车辆优化调度的数学模型, 设计了求解该问题的启发式算法, 应用结果表明, 该算法是可行的。Abstract: Based on analyzing the characteristic of the multiple depot vehicle scheduling (MDVS) problem with full loads, this paper put forward a optimization model, designed heuristic algorithm. Application example shows that this algorithm is feasible.
-
Key words:
- vehicle dispatch /
- multiple depot /
- heuristic algorithm /
- full loads
-
表 1 各车场与重载点及重载点之间的距离
/km Table 1. Distances from full loads sites to each depot and other sites
i j 车场1 车场2 车场3 1 2 3 4 5 6 车场1 - - - 8 1 3 5 4 6 车场2 - - - 7 2 7 9 11 2 车场3 - - - 4 3 2 5 7 8 1 2 3 4 3 6 9 2 3 5 2 1 5 7 11 8 7 1 4 10 3 8 6 2 12 3 8 9 5 6 4 4 9 5 4 10 3 8 6 7 5 3 1 6 3 2 4 7 1 9 6 2 10 9 6 7 8 9 10 1 
下载: 导出CSV
表 2 各重载点所需车次数及各车场空车数
Table 2. Vehicle demands of every full loads site and empty car available in each depot
i 1 2 3 4 5 6 车场1 车场2 车场3 ai 20 15 30 10 8 9 20 30 40
下载: 导出CSV
表 3 初始解
Table 3. Initial solutions
线路标号 行车路线 空驶里程 总里程 π1-π5 车场1-2-4-3-2-4-3-2-车场1 16 86 π6 车场2-6-6-6-6-6-6-6-车场1 10 80 π7 车场2-6-6-1-1-1-1-车场1 20 80 π8 车场3-3-5-5-5-5-5-5-车场2 13 83 π9 车场3-3-5-5-1-1-1-车场1 19 79 π10-π12 车场3-3-3-3-3-3-车场3 32 86 π13 车场3―3-3-3-1-1-车场1 35 85 π14-π15 车场3-1-1-1-1-1-1-车场1 21 81 π16 车场3-1-1-车场1 9 29
下载: 导出CSV
表 4 满意解
Table 4. Satisfactory solutions
线路标号 行车路线 空驶里程 总里程 π1-π5 车场3-3-2-4-3-2-4-3-车场3 18 88 π6 车场1-2-5-5-5-5-5-5-车场2 11 81 π7 车场1-2-5-5-3-2-3-车场3 22 82 π8 车场2-6-6-6-6-6-6-6-车场1 10 80 π9 车场2-6-6-1-1-1-1-车场1 20 80 π10 车场2-2-3-2-3-3-车场3 25 75 π11-π12 车场3-3-3-3-3-3-车场3 32 86 π13-π14 车场3-1-1-1-1-1-1-车场1 21 81 π15 车场3-1-1-1-1-车场1 15 45
下载: 导出CSV
-
[1] Clarke G, Wright J.Scheduling of vehicles from a central depot to number of delivery points[J].Opns.Res., 1964, 12(4):12-18. https://www.cnki.com.cn/Article/CJFDTOTAL-GLXB202007018.htm [2] Gillett B E, Miller L R.A heuristic algorithm for the vehicle dispatch problem[J].Opns.Res., 1974, 22(4):340-349. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC202109012.htm [3] Fisher M L, Jaikumar R.A generalized assignment heuristic for vehicle routing[J].Networks, 1981, 11(2):109-124. https://www.cnki.com.cn/Article/CJFDTOTAL-TDYT202102003.htm [4] JIANG Da-li, YANG Xi-long, DU Wen, et al.A study on the genetic algorithm for vehicle routing problem[J]. Systems Engineering-Theory and Practice, 1999, 19(6):40-44.(in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTGL202001012.htm [5] JIN Hai-he, CHEN Jian, ZHAO Chun-jun.Optimization model for a distribution network and its solution algorithm[J].Journal of Tsinghua University(Science&Technology), 2002, 42(6):739 -742.(in Chinese) doi: 10.3321/j.issn:1000-0054.2002.06.008 [6] HANG Sheng-ce, LI Huai-zu.The generalized assignment model and its decoosition algorithm of multipledepot vehicle scheduling problem(MDVSP)[J].Journal of Xi'an Jiaotong University, 1997, 31(12):111-115.(in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGJS202103013.htm [7] GUO Yao-huang, LI Jun.Vehicle routing with full loads[J]. Journal of Systems Engineering, 1995, 10(2):106-118.(in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL202101017.htm [8] 刑文训, 谢金星.现代优化计算方法[M].北京:清华大学出版 社, 1999. -
点击查看大图
图(4) / 表(4)
计量
- 文章访问数: 500
- HTML全文浏览量: 165
- PDF下载量: 519
- 被引次数: 0
