Derailment analysis of freight train on old Luanhe bridge on Jingshan line in China
-
摘要: 基于列车桥梁时变系统空间振动计算模型及列车脱轨能量随机分析方法, 分别对京山线滦河老桥上行线及下行线货物列车脱轨全过程进行了计算, 采用判别列车脱轨的能量增量准则, 得出下行线货物列车脱轨, 上行线货物列车不脱轨的结论, 此结论与实际符合。同时还对引起该桥下行线货物列车脱轨原因进行了分析, 认为桥梁横向刚度不够是引起脱轨的主要原因, 并指出桥梁横向刚度是保证桥上列车安全运行的主控因素。Abstract: Derailment course of freight train running on the old Luanhe bridge of Jingshan up and down direction line was respectively calculated by the calculation model of special vibration of train-bridge time-variant system and the random energy analysis method of train derailment. Using energy increment criterion, the derailment case of freight train running on down direction line was calculated, and freight train running on up direction line was judged to be not derailed, which correspond to the fact. Meanwhile, the derailment reason of freight train running on down direction line was analyzed. It is pointed that the lack of bridge rigidity is the main reason causing train derailment, and bridge rigidity is the main controlled factor ensuring train's safety running on the bridge.
-
图 2 第一跨跨中上翼缘横向位移波形
Figure 2. Time-history curve of lateral displacement of upper flange in the middle of the first span
图 3 第一跨跨中左腹板竖向位移波形
Figure 3. Time-history curve of vertical displacement of left web plate in the middle of the first span
图 4 第四车第一轴右轮悬浮量波形
Figure 4. Time-history curve of right wheel lift value of the first wheelset of the fourth wagon
图 5 第四车第一轴脱轨系数波形
Figure 5. Time-history curve of derailment coefficient of the first wheelset of the fourth wagon
图 6 第四车第一轴右轮轮重减载率波形
Figure 6. Time-history curve of wheel load reduction rate of right wheel of the fourth wagon
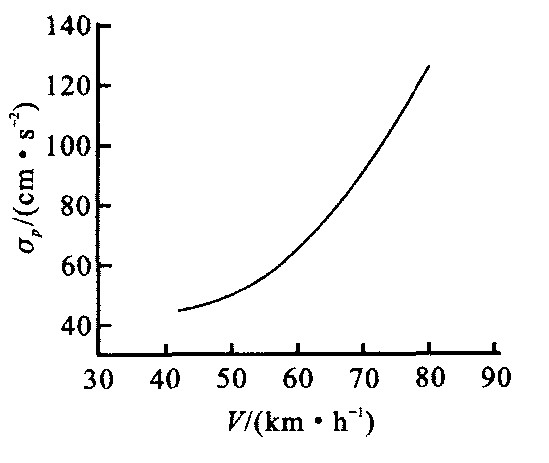
表 1 下行跨中上翼缘横向水平振动幅值实测最大值
Table 1. Measured maximum values of upper flange lateral displacement in down direction
试验编号 机车型号 车辆类型 速度/ (km·h-1) 横向振幅/mm 1201 东风4 货车 50.8 1.106 1206 东风4 货车 52.7 3.847 1207 东风4 货车 49.2 1.870 1208 东风4 货车 51.9 2.679 1209 东风4 货车 42.0 3.180 1212 东风4 货车 53.2 2.855 1214 东风4 货车 54.2 4.120 — 东风4 货车 75.0 12.000 
下载: 导出CSV
表 2 上行跨中上翼缘横向水平振动幅值实测最大值
Table 2. Measured maximum values of upper flange lateral displacement in up direction
试验编号 机车型号 车辆类型 速度/ (km·h-1) 横向振幅/mm 2701 东风4 货车 63.3 1.244 2703 东风4 货车 57.8 1.365 2709 东风4 货车 46.3 0.633 2711 东风4 货车 64.1 1.531 2712 东风4 货车 63.4 5.233 2725 东风4 货车 53.9 1.386 2727 东风4 货车 54.0 1.780 2738 东风4 货车 61.3 1.635
下载: 导出CSV
表 3 全空货物列车振动响应计算最大值
Table 3. Calculated maximum values of vibration responses of train with empty wagons
计算内容 上行线 下行线 机车响应 脱轨系数 0.298 0.310 轮重减载率 0.156 0.215 横向斯佩林指标 2.900 3.010 竖向斯佩林指标 1.966 2.241 空货车响应 脱轨系数 0.690 0.800 轮重减载率 0.416 0.441 横向斯佩林指标 3.018 3.187 竖向斯佩林指标 3.933 4.068 桥梁响应 跨中横向振幅计算最大值/mm 6.200 11.245 跨中横向振幅实测最大值/mm 5.233 12.000
下载: 导出CSV
-
[1] 铁道科学研究院. 铁路行车安全[R]. 北京: 铁道科学研究院, 1998. [2] 俞展猷, 李富达, 李谷. 车轮脱轨及其评价[J]. 铁道学报, 1999, 21 (3): 33—38. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB903.007.htmYU Zhan-you, LI Fu-da, LI Gu. Wheel derailment and its evaluation[J]. Journal of the China Railway Society, 1999, 21(3): 33—38. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB903.007.htm [3] 曾庆元. 列车桥梁时变系统振动分析理论与应用[M]. 北京: 中国铁道出版社, 1999. [4] 曾庆元, 向俊, 娄平. 车桥及车轨时变系统横向振动计算中的根本问题与列车脱轨能量随机分析理论[J]. 中国铁道科学, 2002, 23 (1): 1—10. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200201000.htmZENG Qing-yuan, XIANG Jun, LOU Ping. Fundamental problems in transverse vibration of train-bridge and train-track time-varying system and theory of energy random analysisfor train derailment[J]. Journal of China Railway Science, 2002, 23(1): 1— 10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200201000.htm [5] 向俊, 曾庆元, 娄平. 再论列车脱轨能量随机分析理论[J]. 中国铁道科学, 2002, 23 (2): 26—32. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200201000.htmXIANG Jun, ZENG Qing-yuan, LOU Ping. Further discussion on the energy random analysis of train derailment[J]. Journal of China Railway Science, 2002, 23(2): 26—32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200201000.htm [6] 向俊, 曾庆元. 直线货物列车脱轨过程计算[J]. 铁道学报, 2002, 24 (2): 104—108. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200202026.htmXIANG Jun, ZENG Qing-yuan. Simulation of the derailment courses of freight train on tangent track[J]. Journal of the China Railway Society, 2002, 24(2): 104—108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200202026.htm [7] 北京铁路局. 京山线滦河桥振动试验报告[R]. 北京: 北京铁路局, 1997. -
点击查看大图
计量
- 文章访问数: 298
- HTML全文浏览量: 99
- PDF下载量: 240
- 被引次数: 0
