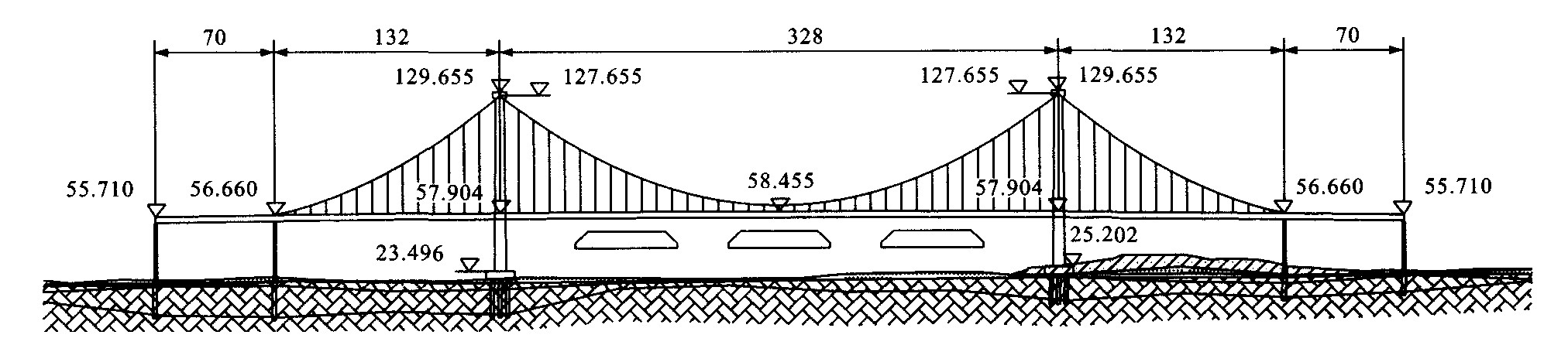
Calculation methods for cable curve of self-anchored suspension bridge
-
摘要: 以长沙市三汊矶湘江大桥为工程背景, 对自锚式悬索桥的主缆线形及无应力长度的计算方法进行了研究, 推导出两种基于不同假定下的主缆线形及无应力索长的计算方法: 假定主缆自重沿跨径均布的抛物线法和假定主缆自重沿弧长均布的分段悬链线法。结果发现: 抛物线法比较简单, 但计算结果比较粗略; 分段悬链线法考虑因素比较全面, 计算相对复杂, 但结果比较精确; 对于空缆线形竖向坐标值两种方法的误差为0.739%, 无应力索长计算两种方法的误差仅为0.31%。结果表明: 抛物线法和分段悬链线法均可应用于自锚式悬索桥的主缆线形计算。Abstract: Took Sanchaji suspension bridge in Changsha as a case study, based on different hypothesis, two methods were deduced, the parabola method of cable gravity distributing uniformly along the span, and the catenaries method of gravity distributing equally along the curve. It is pointed that the parabola method is straightforward, but the results are relatively coarse, and the catenaries method is relatively complicated, but the results are precise, which takes into account all-around factors. For the two methods above, the error of vertical coordinate of cable is 0.739%, and the error of zero-stress length for cable is 0.31%. The results show that the two methods are feasible to calculate the cable curve of self-anchored suspension bridge.
-
图 1 三汊矶自锚式悬索桥桥型布置(单位: m)
Figure 1. Configuration of Sanchaji self-anchored suspension bridge
表 1 材料的物理特性
Table 1. Materials properties
比重γ/ (kN·m-3) 面积A/m2 弹性模量E/ (kN·m-2) 主缆 90.00 0.096 0 1.98×108 吊杆 90.00 0.005 2 1.98×108 加劲梁 172.20 1.091 0 2.10×108 加劲梁加厚段 140.25 1.521 0 2.10×108 
下载: 导出CSV
表 2 悬索桥每延米的重量
Table 2. Cable weight of per meter
位置 主跨 边跨 项目 加劲梁 加劲梁加厚段 二期恒载 加劲梁 加劲梁加厚段 二期恒载 重量/ (kN·m-1) 187.87 213.32 60.5 187.87 213.32 60.5 长度/m 288 40 328 111 21 132
下载: 导出CSV
表 3 分段悬链线法中各索段的参数
Table 3. Parameters of segmental catenaries
位置 中跨 边跨 索段 1 2 3~18 1 2 3~12 13 各索段跨长li/m 11 9 9 12 9 9 9 各索段端部集中力pi/kN 1 373.34 1 179.17 1 121.91 1 441.80 1 179.17 1 121.91 1 308.19
下载: 导出CSV
表 4 主跨及边跨节点坐标对比
Table 4. Comparison of coordinates for two methods
主跨 边跨 桥纵向位置 z 差值/% 桥纵向位置 z 差值/% x 抛物线法 悬链线法 x 抛物线法 悬链线法 0 5.395 5.395 0.000 164 70.995 70.995 0.000 -9 5.593 5.615 0.393 176 61.024 60.953 -0.116 -18 6.185 6.225 0.647 185 54.008 53.930 -0.144 -27 7.173 7.226 0.739 194 47.387 47.322 -0.137 -36 8.556 8.618 0.725 203 41.162 41.110 -0.126 -45 10.334 10.401 0.648 212 35.333 35.294 -0.110 -54 12.507 12.575 0.544 221 29.899 29.874 -0.084 -63 15.075 15.14 0.431 230 24.860 24.847 -0.052 -72 18.039 18.098 0.327 239 20.217 20.215 -0.010 -81 21.397 21.447 0.234 248 15.970 15.977 0.044 -90 25.151 25.189 0.151 257 12.119 12.131 0.099 -99 29.300 29.324 0.082 266 8.663 8.679 0.185 -108 33.844 33.853 0.027 275 5.602 5.618 0.286 -117 38.783 38.775 -0.021 284 2.938 2.949 0.374 -126 44.117 44.092 -0.057 296 0.000 0.000 0.000
下载: 导出CSV
表 5 无应力长度对比
Table 5. Comparison of zero-stress length
项目 有应力长度/m 弹性伸长/m 无应力长度/m 中跨 边跨 中跨 边跨 中跨 边跨 抛物线法 359.628 150.975 0.579 0.254 359.049 150.721 悬链线法 360.165 151.442 0.579 0.254 359.587 151.188 差值/% 0.1 0.3 0 0 0.2 0.3
下载: 导出CSV
-
[1] 李廉锟. 结构力学[M]. 北京: 教育出版社, 1996. [2] 小西一郎(日). 钢桥[M]. 北京: 人民铁道出版社, 1980. [3] 贺栓海. 桥梁结构理论与计算方法[M]. 北京: 人民交通出版社, 2003. [4] 周孟波. 悬索桥手册[M]. 北京: 人民交通出版社, 2003. [5] 邱文亮. 自锚式悬索桥非线性分析与试验研究[D]. 大连: 大连理工大学, 2004. -
点击查看大图
计量
- 文章访问数: 333
- HTML全文浏览量: 178
- PDF下载量: 243
- 被引次数: 0
