Application of genetic algorithm to aircraft sequencing in terminal area
-
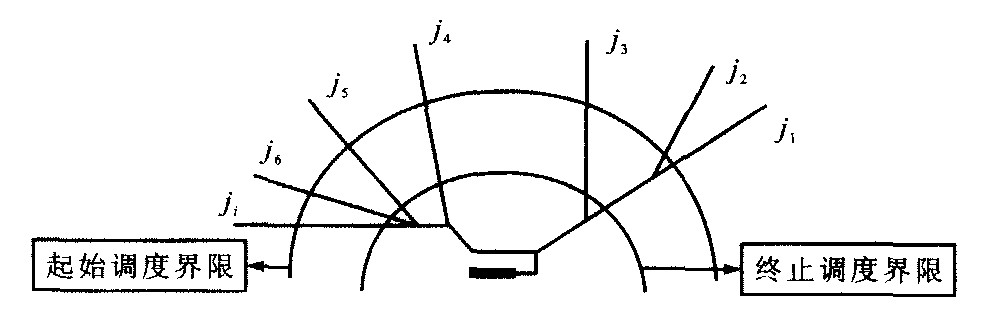
摘要: 研究了遗传算法在终端区跑道分配以及飞机排序中的应用, 建立了多条跑道多架飞机排序的数学模型, 并进行了算例仿真分析。仿真结果表明, 遗传算法与先到先服务排序相比较, 适应度增加了80%, 延时减小了40%, 说明遗传算法的排序结果优于先到先服务的排序结果。Abstract: This paper applied the genetic algorithm (GA) to study runway assignment, sequencing and scheduling of arrival flight in the terminal area, set up a mathematic model of comprising multiple runways and multiple aircrafts. Applied results show that the adaptive degree increasing percent of GA is 80%, the delay time reducing percent of GA is 40%, contrasted with first come first serve (FCFS), which demonstrates that GA is better than FCFS to solve above questions.
-
Key words:
- air traffic control /
- terminal area /
- genetic algorithm /
- aircraft sequencing /
- runway assignment
-
表 1 先到先服务排序仿真结果
Table 1. Simulation result of scheduling using FCFS

表 2 遗传算法排序结果
Table 2. Simulation result of scheduling using genetic algorithm
1号跑道 2号跑道 航班代号 S Emin 延迟时间 航班代号 S Emin 延迟时间 HC8 6.0 6.0 0.0 HC5 6.0 6.0 0.0 HC2 7.0 6.0 1.0 HC3 7.0 6.0 1.0 SC9 9.0 9.0 0.0 HC7 8.0 6.0 2.0 SC4 10.0 9.0 1.0 HC0 10.0 10.0 0.0 LC6 15.0 15.0 0.0 总延误时间=6.5
适应度值=0.133 33LC1 16.5 15.0 1.5 -
[1] Erzberger H, Nedell W. Design of automated system for management of arrival traffic[R]. NASATM 102201, 1989. [2] Neuman F, Erzberger H. Analysis of sequencing and scheduling methods for arrival traffic[R]. NASATM 102795, 1990. [3] Neuman F, Erzberger H. Analysis of delay reducing and fuel saving sequencing and spacing algorithms for arrival traffic[R]. NASA TM 103880, 1991. [4] 刘星, 胡明华, 董襄宁. 遗传算法在飞行冲突解脱中的应用[J]. 南京航空航天大学学报, 2002, 34 (1): 35—39. https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK200201007.htmLIU Xing, HU Ming-hua, DONG Xiang-ning. Application of genetic algorithms for solving flight conflicts[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2002, 34(1): 35—39. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK200201007.htm [5] Erzberger H, Tobias L. A time-based concept for terminal-area traffic management[ R]. NASATM 88243, 1986. [6] Holland J H. Adaptation in Nature and Artificial Systems[M]. The University of Michigan Press, 1975. [7] 黄宝军. 模糊数学方法在空中交通流量管理中的应用研究[D]. 南京: 南京航空航天大学, 1999. [8] 王小平, 曹立明. 遗传算法[M]. 西安: 西安交通大学出版社, 2002. -





 下载:
下载: