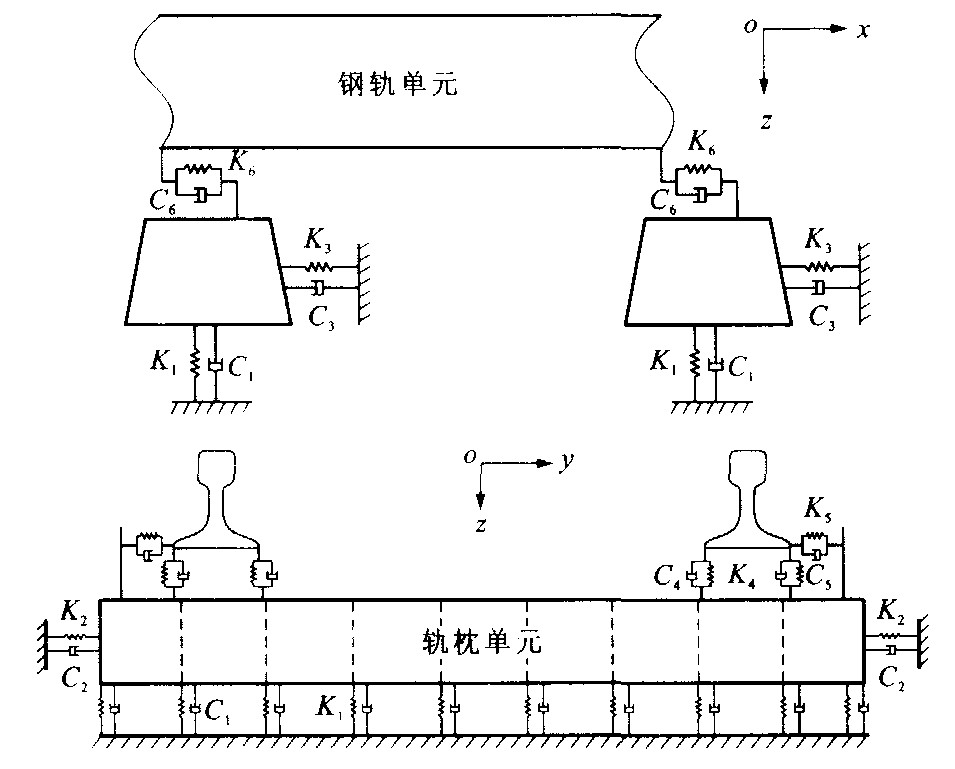
-
摘要: 针对无限长轨道上车辆轨道耦合振动响应特性, 建立了铁路直线轨道结构空间振动模型。采用有限单元法, 将轨枕和钢轨离散为线性粘弹性点支承梁单元, 运用弹性系统总势能不变值原理及形成矩阵的“对号入座”法则, 建立了模型的振动方程组, 采用轨道不断“增加和缩减”方法, 使得模型的质量、阻尼和刚度矩阵及荷载列阵具有时变特性。运用既有的车辆动力学模型和实测参数, 计算了轨道长度为4 km的车辆轨道耦合振动响应值, 钢轨位移、轮对摇摆力以及车体加速度等指标计算幅值与实测幅值接近, 验证了该模型的可行性。Abstract: In order to analyzing the vehicle-track coupling vibration character of infinite length track, a time-varying model of railway tangent track spatial vibration was presented. With finite element method, both the sleeper and the rail were divided by linear viscoelastic discretely supported beam element. The vibration equation group of the model were formulated using the principle of total potential energy with stationary value in elastic system and the "set-in-right-position" rule for formulating matrixes. Using the technique of track being "added and cut down", the mass matrix, damp matrix, stiffness matrix and force vector of the model became time-varying. With the existing vehicle dynamics model and the measurement parameters, 4 km track was applied to calculate the dynamic responses of vehicle-track coupling vibration. The maximum values of!rail displacement, wheelset lateral force and carbody acceleration between calculation and measurement results are very close, which demonstrates the feasibility of the presented model.
-
Key words:
- railway engineering /
- track vibration /
- finite element method /
- viscoelastic support
-
表 1 计算值与实测值比较
Table 1. Comparison of calculation values and measurement values
轨枕横向位移/mm 轨枕竖向位移/mm 钢轨横向位移/mm 钢轨竖向位移/mm 轮对摇摆力/kN 轮轨竖向力/kN 脱轨系数 车体横向加速度/(m·s-2) 车体竖向加速度/(m·s-2) 计算峰值 0.29 1.00 0.37 1.80 15.1 110.2 0.18 0.45 0.75 实测峰值 0.32 1.06 0.41 1.84 16.2 102.7 0.20 0.53 0.80 
下载: 导出CSV
-
[1] 李德建, 曾庆元. 列车-直线轨道空间耦合振动时变系统振动分析[J]. 铁道学报, 1997, 19(1): 101-107. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB701.017.htmLI De-jian, ZENG Qing-yuan. Dynamic analysis of train-tangent-track space-coupling time-varying system[J]. Journal of the China Railway Society, 1997, 19(1): 101-107. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB701.017.htm [2] 雷晓燕, 陈水生. 高速轨道结构空间振动响应分析[J]. 铁道学报, 2000, 22(5): 76-80.LEI Xiao-yan, CHEN Shui-sheng. Space dynamic analysis for track structure of high speed railway[J]. Journal of the China Railway Society, 2000, 22(5): 76-80. (in Chinese) [3] 娄平, 曾庆元. 移动荷载作用下板式轨道的有限元分析[J]. 交通运输工程学报, 2004, 4(1): 29-33. http://transport.chd.edu.cn/article/id/200401008LOU Ping, ZENG Qing-yuan. Finite element analysis of slab track subjected to moving load[J]. Journal of Traffic and Transportation Engineering, 2004, 4(1): 29-33. (in Chinese) http://transport.chd.edu.cn/article/id/200401008 [4] 曾庆元, 郭向荣. 列车桥梁时变系统振动分析理论与应用[M]. 北京: 中国铁道出版社, 1999. [5] 陈果. 车辆-轨道耦合系统随机振动分析[D]. 成都: 西南交通大学, 2000. [6] 娄平, 曾庆元. 移动荷载作用下离散粘弹性点支承长梁的有限元分析[J]. 湘潭矿业学院学报, 2003, 18(1): 36-40. https://www.cnki.com.cn/Article/CJFDTOTAL-XTKY200301010.htmLOU Ping, ZENG Qing-yuan. Finite element analysis of long beam on discrete viscoelastic supports subjected to moving loads[J]. Journal of Xiangtan Mining Institute, 2003, 18(1): 36-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTKY200301010.htm [7] 娄平, 曾庆元. 移动荷载作用下连续粘弹性基础支承无限长梁的有限元分析[J]. 交通运输工程学报, 2003, 3(2): 1-6. http://transport.chd.edu.cn/article/id/200302027LOU Ping, ZENG Qing-yuan. Finite element analysis of infinitely long beam resting on continuous viscoelastic foundation subjected to moving loads[J]. Journal of Traffic and Transportation Engineering, 2003, 3(2): 1-6. (in Chinese) http://transport.chd.edu.cn/article/id/200302027 [8] 李秋义. 高速铁路无缝线路动力稳定性概率分析理论研究[D]. 长沙: 中南大学, 2003. -
点击查看大图
图(13) / 表(1)
计量
- 文章访问数: 439
- HTML全文浏览量: 156
- PDF下载量: 423
- 被引次数: 0
