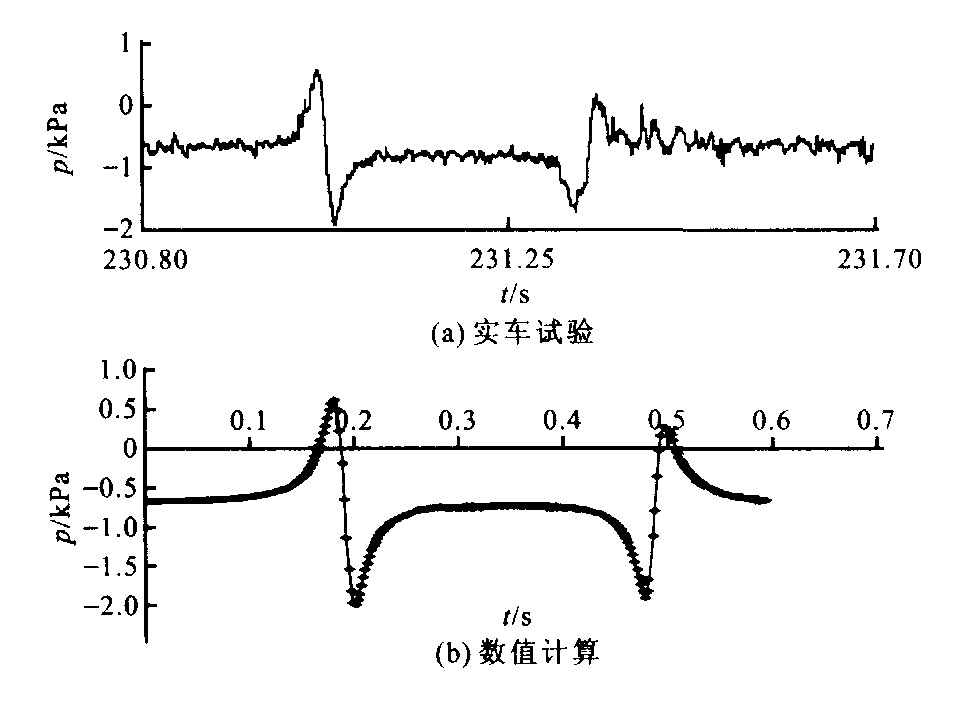
-
摘要: 为了研究气动力对磁浮列车运行稳定性的影响, 以上海磁浮列车为研究对象, 采用动网格技术, 通过求解三维可压缩非定常N S方程对磁悬浮列车在相对速度860 km/h交会时的气动力进行数值模拟; 同时将车体、悬浮架作为弹性体, 悬挂系统作为弹簧阻尼单元, 建立了详细的系统动力学模型, 对考虑列车交会瞬态压力冲击作用下的高速磁浮列车进行了横向振动分析。计算结果表明, 流场数值计算出的最大压力波幅值与实车试验结果两者差距小于6%;仅考虑轨道不平顺时, 磁浮列车的横向振动较小, 而在考虑磁浮列车高速运行时产生的交会压力波的情况下, 车体却产生了较大的横向振动, 底架最大横向加速度达1 5 m/s2, 经过二系悬挂的缓冲作用后振动明显减小, 悬浮架最大横向振动加速度约为0 7 m/s2。Abstract: Using the 3-D compressible N-S equations and dynamic mesh, the train passing pressure pulse of Shanghai maglev train at the relative speed of 860 km/h was analyzed in order to know the aerodynamic force's influence on the stability of maglev train. A detailed dynamic model was established, where the carbody was considered as elastic body while the suspension system was considered as spring-damp element. The transverse vibration considering the train passing pressure pulse was calculated. The results show that the difference of the maximal pressure pulse between numerical calculation and real car test is less than 6%, and the transverse vibration only arosed by the irregularity of rail track is little. It is great if the influence of train passing pressure pulse is considered, and the underframe's maximal transverse acceleration is 1.5 m/s2. The suspension bogies' acceleration reduce to 0.7 m/s2 under secondary suspensions' buffer action.
-
Key words:
- maglev train /
- train passing pressure pulse /
- fluid calculation /
- transverse vibration
-
图 1 实车试验与数值计算交会压力波比较
Figure 1. Pressure pulses comparison of real car test and numerical calculation
图 9 悬浮架横向加速度-时间曲线
Figure 9. Curves of suspension bogies's transverse acceleration vs time
图 11 底架横向位移-频率曲线
Figure 11. Curves of underframe's transverse displacement vs frequency
图 12 悬浮架横向位移-频率曲线
Figure 12. Curves of suspension bogies' transverse displacement vs frequency
图 14 底架横向加速度-频率曲线
Figure 14. Curves of underframe's transverse acceleration vs frequency
图 15 悬浮架横向加速度-频率曲线
Figure 15. Curves of suspension bogies' transverse acceleration vs frequency
表 1 结果输出曲线描述
Table 1. Description of results output curves
曲线1——车顶前端位移(加速度) 曲线2——车顶中部位移(加速度) 曲线3——车顶后端位移(加速度) 曲线4——侧墙前端位移(加速度) 曲线5——侧墙中部位移(加速度) 曲线6——侧墙后端位移(加速度) 曲线7——底架前端位移(加速度) 曲线8——底架中部位移(加速度) 曲线9——底架后端位移(加速度) 曲线10——悬浮架1位移(加速度) 曲线11——悬浮架2位移(加速度) 曲线12——悬浮架3位移(加速度) 曲线13——悬浮架4位移(加速度) 
下载: 导出CSV
表 2 分析结果
Table 2. Analysis result
阶数 频率/Hz 振型 1 6.6 侧墙1阶横向弯曲 2 7.0 车体点头 3 9.6 车体1阶垂向弯曲 4 10.0 车体局部 5 10.4 车体抬头 6 13.3 车顶2阶扭转
下载: 导出CSV
-
[1] 田红旗, 姚松, 姚曙光. 列车交会压力波对车体和侧窗的影响[J]. 中国铁道科学, 2000, 21(4): 6-12. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200004001.htmTIAN Hong-qi, YAO Song, YAO Shu-guang. Influence of the air pressure pulse on car-body and side-windows of two meeting trains[J]. China Railway Science, 2000, 21(4): 6-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200004001.htm [2] 高广军, 田红旗, 张健. 横风对双层集装箱平车运行稳定性的影响[J]. 交通运输工程学报, 2004, 4(2): 45-48. http://transport.chd.edu.cn/article/id/200402011GAO Guang-jun, TIAN Hong-qi, ZHANG Jian. Cross-wind affection on double container train[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 45-48. (in Chinese) http://transport.chd.edu.cn/article/id/200402011 [3] 吴望一. 流体力学[M]. 北京: 北京大学出版社, 1998. [4] 刘堂红. 高速磁浮列车动态响应分析[D]. 长沙: 中南大学, 2003. [5] 武青海, 俞翰斌, 李和平. 磁悬浮列车空气动力学仿真计算探讨[J]. 铁道机车车辆, 2004, 24(2): 18-20. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJC200402003.htmWU Qing-hai, YU Han-bin, LI He-ping. A study on numerical simulation of aerodynamics for the maglev train[J]. Railway Locomotive& Car, 2004, 24(2): 18-20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJC200402003.htm [6] 李人宪, 翟婉明. 磁悬浮列车横风稳定性的数值分析[J]. 交通运输工程学报, 2001, 1(1): 99-101. http://transport.chd.edu.cn/article/id/200101025LI Ren-xian, ZHAI Wan-ming. Numerical analysis of crosswing stability of magnetically levitated trains[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 99-101. (in Chinese) http://transport.chd.edu.cn/article/id/200101025 [7] 姚曙光, 许平. 高速磁浮列车车体国产化[J]. 交通运输工程学报, 2004, 4(2): 40-44. http://transport.chd.edu.cn/article/id/200402010YAO Shu-guang, XU Ping. Chinese domestic components of high-speed maglev train body[J]. Journal of Traffic and Transportation Engineering, 2004, 4(2): 40-44. (in Chinese) http://transport.chd.edu.cn/article/id/200402010 [8] 王亚丽. 轨道随机不平顺对高速动力车的响应分析[D]. 长沙: 中南大学, 2002. -
点击查看大图
计量
- 文章访问数: 400
- HTML全文浏览量: 176
- PDF下载量: 387
- 被引次数: 0
